基于CGLCM和GA-SVM的混凝土图像分类方法 *

张 莉， 焦宇倩， 续 婷， 侯宇超， 白艳萍， 李建军

(1. 中北大学 理学院， 山西 太原 030051； 2. 中北大学 信息与通信工程学院， 山西 太原 030051)

0 引 言

混凝土配合比的设计是混凝土材料设计的基础， 它直接影响混凝土结构设计要求的强度、 施工所要求的混凝土拌合物的和易性、 耐久性要求等， 并保证不同用途混凝土所要求的质量. 目前， 关于混凝土裂缝检测[1-3]的研究比较多， 而针对混凝土配合比图像识别的研究还很少. 图像分类主要分三步， 分别是图像预处理、 图像特征提取、 图像分类. 混凝土图像特征提取与分类是本文研究的重点. 由于纹理是由灰度分布在空间位置上反复出现而形成的， 因而在图像空间中相隔某距离的两像素之间会存在一定的灰度关系， 即图像中灰度的空间相关特性. 灰度共生矩阵就是一种通过研究灰度的空间相关特性来描述纹理的常用方法[4]. 王民等[4]提出了一种多尺度灰度共生矩阵的纹理特征提取方法， 分别提取HSI色彩分量的灰度共生矩阵纹理特征， 实现了对中国画的分类. 朱琳等[5]结合灰度共生矩阵理论对CT混凝土图像在不同荷载作用下的细观损伤演化过程进行了说明. Relly Andayani等[6]利用灰度共生矩阵纹理特征值对混凝土塌落度进行了分类. Asha Gowda Karegowda等[7]利用彩色共生矩阵， 提高了图像检索的性能. 王辉等[8]利用彩色共生矩阵的方法实现了对木质板材的分类.

根据上述研究发现， 单纯采用灰度共生矩阵进行图像纹理特征提取， 会导致颜色信息的损失， 识别精度较低. 而用彩色共生矩阵进行图像特征提取， 融合了颜色特征， 具有较强的鲁棒性， 可以弥补其他特征的不足. 本文提出一种基于彩色共生矩阵和支持向量机的混凝土图像识别方法， 获得了较为满意的识别精度.

1 混凝土数据集

选用的两种数据集均来自于中北大学土木工程专业构建的数据集， 每一张图像都是同一样本在不同拍摄角度下得到的. 其中CIRD_A的获取时间为2019年11月， 共有12类混凝土图像； CIRD_B的获取时间为2020年3月， 共有33类混凝土图像.

1.1 CIRD_A

该数据集中混凝土的配合比有3种， 分别为 4∶6， 5∶5， 6∶4； 粒径范围有4种， 分别为： 0.3 mm～0.6 mm， 0.6 mm～1.18 mm， 1.18 mm～2.36 mm， 2.36 mm～4.75 mm. 选取表1 所列的9类混凝土图像.

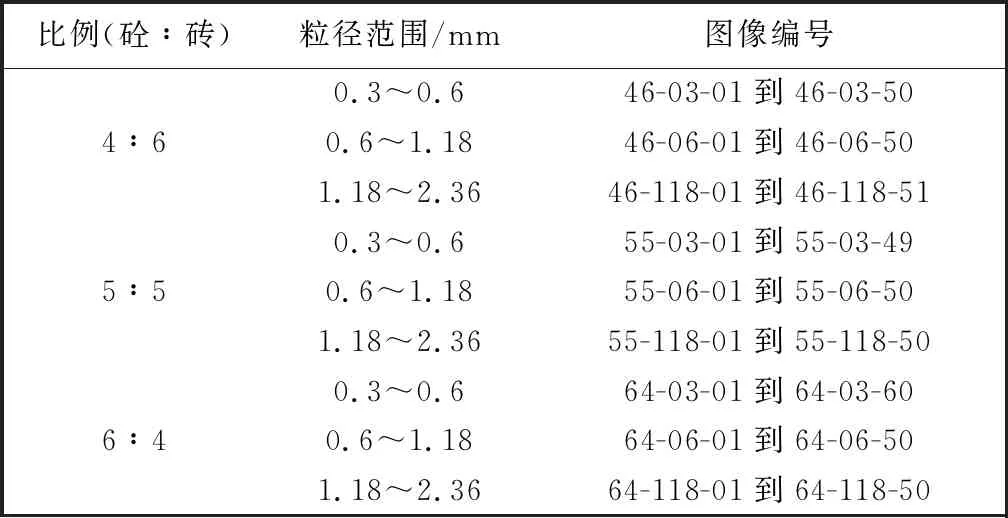
表1 CIRD_A文件目录

1.2 CIRD_B

该数据集中混凝土的配合比有11种， 分别为 0∶1， 1∶9， 2∶8， 3∶7， 4∶6， 5∶5， 6∶4， 7∶3， 8∶2， 9∶1， 1∶0； 粒径范围有3种， 分别为： 0.075 mm～0.3 mm， 0.3 mm～0.6 mm， 0.6 mm～1.18 mm. 选取表2 所列的9类混凝土图像.

表2 CIRD_B文件目录

1.3 图像处理

由于混凝土图像存在多余背景， 我们利用PS软件中的裁切工具对这72张图片进行处理. 将裁剪出的不规则四边形目标图像调整成2 000*2 000分辨率图片进行保存(原始图像大小为： 4 752*3 168像素). 目前两种数据集中混凝土图像样本数较少， 因此采用步长裁剪的方式扩充数据集. 选择步长为230， 将图像裁剪成 280*280分辨率的图片， 可以满足混凝土图像的真实配比， 有利于特征的有效提取. 图 1 为原始图像和裁切无关背景后的图像.

图 1 图像处理示例图

2 基本原理

2.1 遗传算法优化支持向量机模型

2.1.1 遗传算法

遗传算法最早是由Holland教授根据达尔文的进化论所提出的一种高效启发式搜索方法[9]. 它通过遗传中的选择、 交叉、 变异等操作产生下一代的解， 使适应度函数值高的个体被保留， 并逐渐淘汰适应度函数值低的个体， 如此循环， 就能得到满足条件的解， 达到优化目的.

2.1.2 SVM理论

支持向量机是由Vapnik于1995年提出的一种机器学习理论， 可用于回归分析与分类[10]. 其分类思想是将低维空间中线性不可分的数据样本映射到高维空间使其线性可分， 并在高维空间中找到一个最优超平面， 使得不同类别数据点之间的距离最大化.

设n个样本集{((xi,yi)|i=1,2，…，n)}，xi∈Rn，yi∈{-1,+1}，xi为训练样本点，yi为其对应标签.使y=+1类与y=-1类数据点的间隔最大的超平面为

ωTxi-b=0,i=1,2，…，n.

(1)

为了保证数据点xi所允许的偏离差最小， 引入松弛变量ξi(ξi≥0)， 惩罚因子c, 得到如式(2)的目标函数

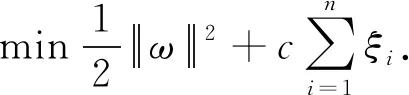
(2)

为了处理非线性数据， 选用RBF核函数对SVM进行推广， 利用此函数将样本映射到高维空间， 使得线性分类的精确率提升. RBF核函数公式为

(3)

式中：g为核函数半径.

(4)

根据给定的RBF核函数， SVM分类器表示为

F(x)=sgn(f(x)),

(5)

式中：f(x)为SVM分类超平面决策函数.

(6)

2.1.3 优化模型

为了提升SVM的分类器性能， 提高分类精确率， 通过使用遗传算法优化支持向量机， 实质上就是通过此方法寻找到合适的惩罚因子c及核函数半径g[10]. 优化步骤如下：

1) 对支持向量机中的参数c,g进行二进制编码， 并产生初始种群；

2) 对种群进行选择、 交叉、 变异操作及计算适应度函数， 若满足GA终止条件， 直接输出最优参数组合(cbest=29.56，gbest=0.25)；

3) 将参数cbest,gbest代入SVM进行训练及测试集分类， 判别是否符合实验设定的精度， 如不满足， 返回步骤2)；

4) 利用最优参数， 建立混凝土图像分类的GA-SVM模型， 对测试集利用满足精度的GA-SVM模型进行分类， 并输出结果.

如图 2 为GA算法优化SVM模型的参数寻优适应度曲线， 从图中可以看出， GA算法具有良好的收敛性能和寻优效率.

图 2 参数寻优适应度曲线

2.2 灰度共生矩阵(GLCM)

灰度共生矩阵是在20世纪70年代由Haralick[11]首次提出的， 自此被广泛应用于纹理特征提取. 它是通过研究具有一定距离像素对之间的空间相关性来表述图像纹理特征. 由于灰度共生矩阵计算量较大， 一般不直接应用， 而是在此基础上采用二次统计量描述纹理信息. Haralick提出了14种灰度纹理特征参数(Haralick特征能数)， 本文使用了其中的8种， 分别是二阶矩、 对比度、 相关性、 逆差距、 均值和、 熵、 和方差与差方差.

灰度共生矩阵是图像的一种二阶统计量. 给定一副数字图像I(x,y)， 其灰度级为L， 则灰度共生矩阵G(x,y)中(i,j)的值被定义为I(x,y)在θ方向上， 间隔为d的两个像素点对(i,j)的统计数目n.G(x,y)的尺寸为L×L，n为灰度共生矩阵在G(i,j)的像素值. 图 3 为0°方向上的8级灰度共生矩阵构造.

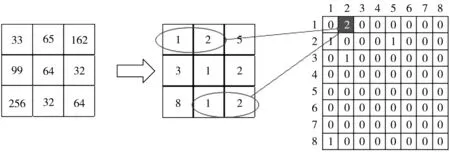
图 3 0°方向上的8级灰度共生矩阵构造

2.3 彩色共生矩阵(CGLCM)

彩色共生矩阵的概念最早是由Palm[12]提出的， 其将颜色和纹理相结合的方法归结为平行法、 顺序法和综合法. 平行法和顺序法是将颜色和纹理作为独立的图像特征进行融合分析， 这样势必会造成原始彩色图像信息的损失； 综合法是指从某幅原始彩色图像中获取各个颜色通道的伪灰度图像， 分别提取各伪灰度图像的灰度共生矩阵纹理特征参数， 用这些提取出来的纹理特征参数描述原始彩色图像纹理. 本文采用综合法.

彩色共生矩阵构造步骤[13]如下：

1) 颜色空间选择. 颜色空间的选择对于彩色图像的识别是一个至关重要的环节. H(色调)， S(饱和度)， V(明度)空间能够更加贴近人类的视觉感知. HSV颜色空间是一个均匀的六角椎体模型， 模型的 3个坐标是独立的， 能够把HSV各个分量的变化表现得很清晰.

图 4 混凝土图像的HSV分量及其共生矩阵

2) 颜色空间转换. 将原始混凝土图像从RGB空间转换到HSV空间.

3) 对HSV空间中的每个颜色通道H， S， V分别构造灰度共生矩阵， 并计算2.2节中提到的8个 Haralick特征参数.

图 4 为混凝土图像的HSV分量及其构造的共生矩阵图像.

3 混凝土图像纹理特征提取与分析

3.1 纹理特征提取

借助彩色共生矩阵的思想， 提出一种新的获取混凝土图像纹理特征的方法. 具体的操作步骤如下：

1) 将预处理后得到的混凝土图像全部转换到HSV空间， 并提取H， S， V 3个色彩分量， 得到的图像定义为伪灰度图像. 对9类混凝土图像H分量的伪灰度图像分别提取8个特征参数， 并用A，B，C，D，E，F，G，H代替. 例如Anm，n为混凝土图像的类别；m为对应的色彩分量，m为1时表示H，m为2时表示S，m为3时表示V. 得到如下8维特征矩阵.

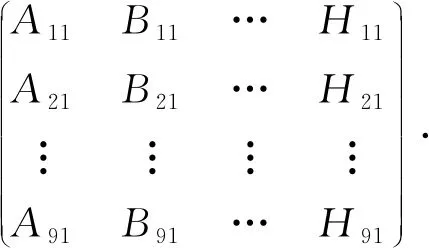
(7)

2) 对S，V色彩分量重复步骤1)， 这样就得到了混凝土图像3个色彩分量所对应的特征矩阵.

3) 将3个特征矩阵进行融合， 可以得到了一个 24维的特征矩阵为

3.2 特征分析

特征分析是目标识别、 图像分割和图像分类中的重要方法. 本研究应用MATLAB2014a软件编写的程序来计算混凝土彩色图像的特征参数均值.

图 5 所示为CIRD_B中9类混凝土图像彩色共生矩阵特征参数曲线. 由图 5 可知， 彩色共生矩阵3个颜色通道的这8个特征参数与混凝土图像不同类别之间存在着较大的差异， 因此， 利用这些信息， 能够很好地获取每一类混凝土图像样本的颜色及纹理信息. 因此， 本文方法是可行的.

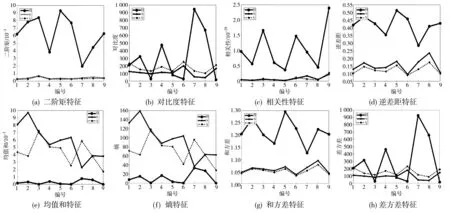
图 5 CIRD_B中9类混凝土图像彩色共生矩阵特征参数曲线

4 实验结果及分析

4.1 实验样本

选取预处理后的CIRD_B中的混凝土图像(随机选取训练集70%， 测试集30%)进行识别， 验证彩色共生矩阵提取特征应用于混凝土图像分类的有效性. 图 6 所示为CIRD_B中9类混凝土图像. 由于篇幅限制， 不再给出CIRD_A.

图 6 CIRD_B中的9类混凝土图像

4.2 实验流程图

根据本文提出的彩色共生矩阵方法， 绘制了如图 7 所示的流程图.

图 7 分类方法框架图

4.3 实验结果分析

彩色共生矩阵容易受到步长d、 颜色空间、 灰度级以及方向等参数的影响. 方向参数选取0°， 45°， 90°， 135° 4个方向特征值的平均值， 这样能大大减少方向对特征参数的影响[14]. 选择SVM进行分类， 通过多组对比试验， 分析步长、 颜色空间、 灰度级等参数对实验结果的影响.

4.3.1 步长d对实验结果的影响

颜色空间选择HSV， 灰度级选择256步， 讨论步长d对实验结果的影响， 这样有利于保持混凝土图像的最大信息量， 保证特征参数的有用性. 由于步长d较大时， 会导致大量像素点不参与灰度共生矩阵运算， 造成纹理信息不准确， 本实验中d最大为5.CIRD_B不同步长的分类精确率见表3.实验结果表明， 当d=2时效果最好， 合适的步长有利于灰度共生矩阵更好地描述混凝土图像特征.

表3 CIRD_B不同步长的分类精确率

4.3.2 颜色空间对实验结果的影响

颜色空间的选择和建立对获取混凝土图像的色彩特征具有重要作用， 合适的色彩空间能够有效地获取样本的色彩特征. 本研究选择几种常见的颜色空间并结合灰度共生矩阵来获取特征. 其中， 步长d=2， 灰度级为256， 选取的颜色空间为HSV， HSI， RGB， 分类精确率见表4. 实验结果表明， 颜色空间为HSV效果最好.

表4 CIRD_B不同颜色空间的分类精确率

4.3.3 灰度级对实验结果的影响

步长d=2， 颜色空间选择HSV空间， 灰度级选择16， 32， 64， 128， 256时的分类精确率见表5. 实验结果表明， 当灰度级为256时效果最好. 图像的灰度级越大， 图像纹理越清晰， 越能保留混凝土图像的真实信息.

表5 CIRD_B不同灰度级的分类精确率

4.3.4 基于CGLCM与多种分类器的两种数据集混凝土图像识别

根据步长、 颜色空间、 灰度级3组对比实验结果， 得到了较为合适的彩色共生矩阵参数值： 步长d=2， 灰度级为256， 颜色空间为HSV. 为了进一步验证彩色共生矩阵(CELCM)的有效性， 将它与传统灰度共生矩阵(GLCM)进行比较， 并且对比了不同分类器对实验结果的影响. 由于BP神经网络也是一种经典的分类器， 故将BP神经网络也加入到对比实验中. 每种分类器分别对两种数据集进行50次实验， 并取精确率的平均值， 结果见表6. 实验结果表明， 两种数据集采用CGLCM与GA-SVM的分类效果最好.

表6 两种数据集下传统GLCM与CGLCM的分类精确率

5 结 论

本文选用了两种混凝土图像数据集， 提出了一种基于彩色共生矩阵支持和基于向量机的分类方法. 利用彩色共生矩阵提取24维特征向量， 将其输入到BP神经网络、 SVM、 PSO-SVM、 GS-SVM、 GA-SVM中. 实验结果表明， CIRD_A和CIRD_B在GA-SVM上的识别精度最好， 分别可以达到 97.76%， 96.34%， 远超其他分类器， 用该方法识别混凝土图像是可行的.