微小初始角度的多段式泊车路径规划 *
毕 锟, 范 英
(太原科技大学 交通与物流学院, 山西 太原 030024)
0 引 言
随着我国汽车保有量不断增加, 停车空间越来越小, 增加了泊车过程中交通事故的发生几率, 也对驾驶员的操作水平提出了更高的要求.
自动泊车是增加驾驶员舒适性和安全性的解决方案. 自动泊车系统的一个关键部分是泊车路径规划, 对此, 国内外很多学者进行了大量的研究. Su B等[1]提出了一种基于端点区域化的二次平行自动停车方法,建立了避障约束条件的泊车路径函数, 并用遗传算法以泊车路径函数为目标函数进行了优化, 但其估算最小车位会使结果造成一些误差; Vorobieva H等[2]提出了一种使用回旋曲线将圆弧路径转换为连续曲率路径的微小车位乘用车自动平行泊车系统; Wang L X等[3]提出了一种使用两个不同半径切向圆弧的从任意初始角度自动平行泊车的算法, 该方法可以从任意初始角度实现泊车, 但泊车起始区域过大, 不适合实际运用; Ge Y R等[4]提出了一种从任意起始位姿经过中间过渡位姿到达目标位姿的自动平行泊车运动规划算法; 陈无畏等[5]规划了一种双向的3段弧泊车路径, 并用遗传算法对其进行了优化; 胡文等[6]基于熟练驾驶员泊车经验, 设计了一种新的自动泊车规划算法, 但需要较多驾驶员泊车经验样本; 钱立军等[7]提出了泊车过程中方向盘匀速转动的策略, 对比分析五段式路径和两段式路径在泊车过程中的车速、 转角、 油门控制量、 刹车控制量随时间的变化关系, 证明五段式泊车过程更加连贯, 但未考虑方向盘转角随时间变化等因素; 王启明[8]和胡勤明等[9]为了解决泊车轨迹的曲率突变问题, 提出了多段式泊车路径, 并对其进行了优化处理; 郭夜啼[10]提出了一种多段式曲线拟合的平行泊车路径规划方法, 采用不同的起始点进行泊车仿真, 但没有考虑车辆存在一定初始角度时的泊车问题.
以上文献都是在平行初始状态下规划的泊车路径, 没有考虑到在实际泊车环境中待泊车车辆总会与目标车位存在初始泊车角度的问题. 为了解决车辆初始泊车状态与车位存在一定角度而导致泊车失败的问题, 提出了一种多段式平行泊车路径规划方法, 以实现汽车与车位存在一定初始角度时, 仍能保证其不与周边环境发生碰撞且泊车入位, 并通过MATLAB仿真验证了该方法的可行性.
1 车辆低速运动学模型
在泊车过程中, 由于车速较低, 可忽略车轮的滑移和侧偏. 假定车轮运动状态均为滚动, 根据阿克曼转向原理, 构建车辆运动学模型[11], 如图 1 所示.
在参考坐标系中, 车辆绕旋转中心O以R为半径转动,l为轴距,δ为车轮中心点等效转角,θ为车身转向角,vf为前轮中心点速度,vr为后轮中心点速度, 汽车前轴中心点坐标为(xf,yf), 后轴中心点坐标为(xr,yr).
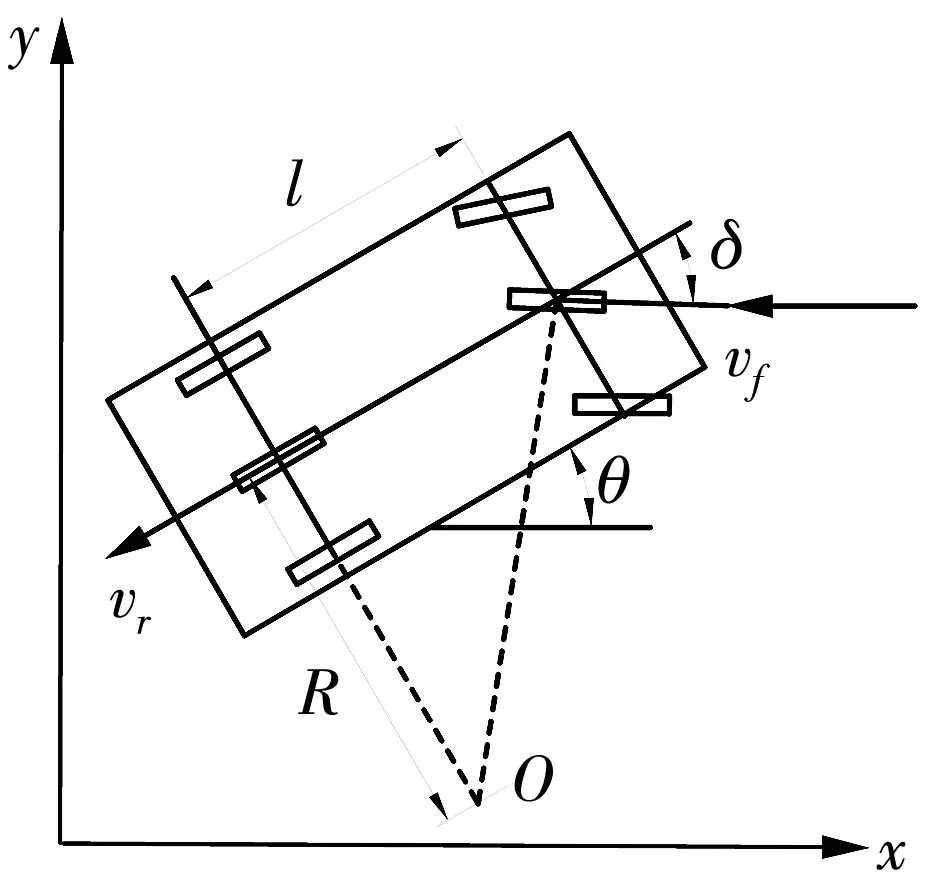
图 1 车辆运动学模型
由于忽略了车辆轮胎的滑移现象, 后轮运动方向与车辆垂直的方向速度为0, 所以有

(1)
根据几何关系推导后轴中心点和前轴中心点关系得
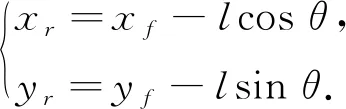
(2)
前后轴中心速度满足关系
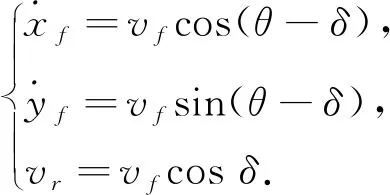
(3)
取车辆后轴中心点速度v为整车速度, 可以得到以后轴中心为参考点的运动学模型[12]

(4)
2 碰撞分析
为了保证车辆能够安全地停进车库, 在规划泊车路径之前, 需要对车辆和泊车环境进行防碰撞分析, 这也是实现无碰撞泊车的关键[13]. 为了便于避障分析, 将车辆简化成一个长方形, 如图 2 所示. 其中, 点A,B,C,D分别是车辆的4个顶点在地面的投影点; 点a,b,c,d分别为车位在地面的投影点; 点O1为第一段圆弧轨迹的转动中心; 点O2为第二段圆弧轨迹的转动中心; 点P,Q分别为后轴中心点和前轴中心点; 点E为后轴的延长线与车辆右侧边界的交点在地面的投影点; 点F为车辆前轴延长线与车辆右侧边界的交点在地面的投影点; 点M和点N分别为车辆后轴和前轴延长线与车辆左侧边界的交点在地面的投影点.根据驾驶员泊车经验可知, 车辆在平行泊车过程中, 最容易发生碰撞的是车辆的点B,C,D和E.

图 2 微小初始角度平行泊车碰撞分析示意图
2.1 车辆第一段曲线运动轨迹碰撞分析
2.1.1E点碰撞分析
车辆方向盘向右打泊车过程中, 车辆以点O1为圆心,R1为半径转动, 车辆右侧边界最容易和车位右侧发生碰撞.将点A,B,C,D,E与圆心O1连接起来, 根据几何关系, 可以发现连线O1E最短, 说明车辆右侧最容易发生碰撞的点是点E.以车位左侧最上方的边界点a(xa,ya)为原点, 建立X-Y平面直角坐标系, 以后轴中心点P为参考, 分析点E与车位右侧的碰撞过程.E1为车辆与车位的碰撞临界点, 将轮胎整个运动过程视作纯滚动运动, 根据阿克曼转向原理, 转动中心点O1在后轴延长线上, 所以有

(5)
假设车辆右侧点E与车位右侧边界临界碰撞时, 后轴中心点P坐标为(XP,YP), 车辆的航向角为θ.
第一段曲线转动中心与车辆后轴中心的坐标关系为
(6)
根据几何关系可以知道两条直角边的长度分别为

(7)
CE=L-Lr.
(8)
车辆不发生碰撞的条件为
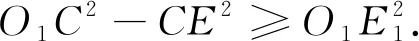
(9)
根据以上公式可以得出不发生碰撞的条件为
(R1-0.5W)2≥(XP+R1sinθ-Ll)2+
(YP-R1cosθ)2,
(10)
式中:Ll为目标车位的长;W为车宽.
2.1.2B点碰撞分析
第一段圆弧轨迹泊车过程中, 车辆的B点容易与目标车位右侧车位上边界发生碰撞, 为了避免发生碰撞, 需要满足约束条件
O1B≥O1d.
(11)
根据几何关系可得
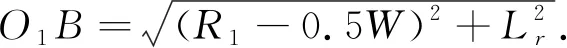
(12)
将式(7), 式(12)代入式(11)中可知需要满足
(YP-R1cosθ)2.
(13)
2.1.3D点碰撞分析
为了防止车头与车位对面道路边界障碍物或者道路另一侧行驶的车辆发生碰撞, 需要就此建立车辆约束条件, 避免车辆越过对面道路边界, 保证车辆泊车安全. 在平行泊车过程中, 车辆左侧最容易与对面道路边界发生碰撞的点是点D.D1为车辆与道路边界的碰撞临界点,H为车位对面道路的宽度, 不发生碰撞的条件为
O1D+YO1≤H.
(14)
根据几何关系可得
O1D2=O1M2+MD2,
(15)
O1M=R1+0.5W,
(16)
MD=L-Lr.
(17)
将式(13), 式(14)代入式(12)中可以得到
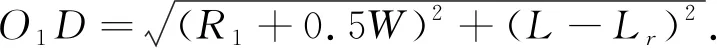
(18)
将式(18)和点O1的纵坐标代入式(14)可以得出,D点不发生碰撞的条件为
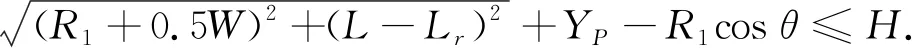
(19)
2.2 车辆第二段曲线运动轨迹碰撞分析
2.2.1C点碰撞分析
车辆方向盘向右打的状态下, 泊车到达合适位置后, 向左转动方向盘, 由此执行整个泊车过程的第二段曲线运动. 车辆以点O2为圆心,R2为半径转动, 车辆在这段运动过程中, 最容易发生碰撞的是车辆右侧边界的两个顶点B和C.在泊车入位过程中, 汽车车身右侧顶点C容易与车位右顶点d发生碰撞,C1为车辆与车位的碰撞临界点,Ll为目标车位的长,Lw为车位宽,Lf为前悬,Lr为后悬, 第二段曲线转动中心与车辆后轴中心的坐标关系为
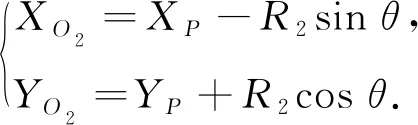
(20)
防止发生碰撞的约束条件是
O2C≤O2d.
(21)
因为
O2C1=O2d,
(22)
根据以上各点坐标, 可以得到无碰撞约束条件为
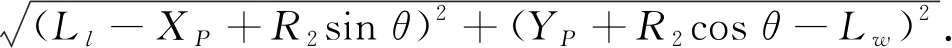
(23)
2.2.2B点碰撞分析
在平行泊车最后阶段, 车辆绕转动中心O2转动, 车辆尾部顶点B容易与车位的底部边界发生碰撞, 根据几何关系可以得出
O2B2=O2E2+BE2,
(24)
O2E=R2+0.5W.
(25)
将式(25)代入到式(24)中得
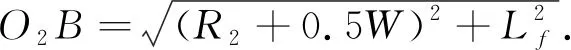
(26)
满足车尾B点不与车位底部发生碰撞的条件为
O2B≤YO2+Lw.
(27)
可以得到, 需要满足

(28)
2.3 最小安全车位
为了防止车辆在停车过程中与停车位周围环境发生碰撞和保证车辆顺利泊进车位, 不但要求泊车入位过程的路径规划水准, 还要求停车位足够大, 能容许车辆停进去. 显然, 停车位的尺寸必须大于车辆的尺寸. 但是在实际泊车过程中, 必须根据车辆的性能和避碰约束条件来具体分析车辆能够顺利泊车入位的最小停车位大小.
根据以上的车辆碰撞分析, 停车位与车辆和碰撞点之间的相对位置如图 3 所示, 车辆的右前顶点C可能在C1点与车位发生碰撞, 车辆的右后顶点B可能在点B1与车位发生碰撞, 为了确保泊车安全, 设定车辆轮廓与车位边界之间的安全距离分别为Δl1, Δl2, Δd1和Δd2. 可以得出停车位的长和宽分别为
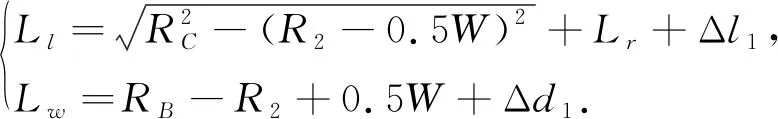
(29)

图 3 最小安全车位
3 泊车起始区域划分
自动泊车的起始区域也是整个泊车过程的关键内容之一, 起始区域的好坏很大程度上决定着泊车的成功与否. 为了顺利实现泊车过程的第一步, 提高泊车成功率, 本文根据倒车入库过程, 车辆右侧边缘BC和车辆左前顶点D的碰撞分析, 对泊车的起始区域进行了划分.
通过多段式泊车路径进行可行泊车起始区域分析, 当车辆在第二段直线行驶时, 根据车辆结构参数和泊车路径可知第二段直线终点P3的坐标为
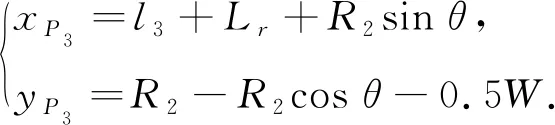
(30)
直线P2P3的表达式为
y=tanθ(x-xP3)+yP3,
(31)
则车辆右侧顶点B的运动轨迹方程为
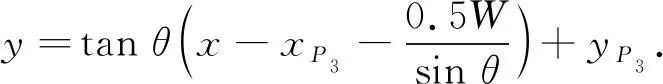
(32)
为了避免车辆右侧边缘与车位顶点发生碰撞, 需要满足点d与直线BC的距离不小于0, 即
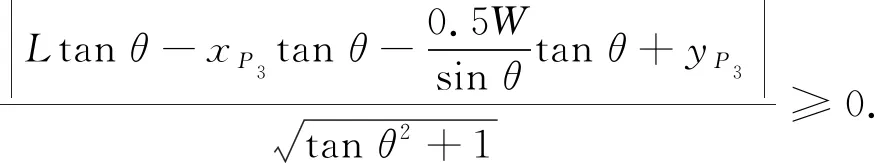
(33)
车辆在沿圆弧P1P2行驶时, 左前顶点D不能越过车位对面的道路边界, 即要满足
RD+yO1≤H。
(34)
4 平行车位泊车路径规划
如图 4 所示, 开始进行五段式平行泊车,P0点为车辆后轴中心的泊车初始位置点, 车辆的初始航向角为θ, 泊车时车轮为回正状态.

图 4 车辆后轴中点轨迹示意图
针对泊车过程车辆的初始状态可能与车位存在夹角导致泊车失败的问题, 本文分别对 3种不同的车辆初始状态进行路径规划. 视逆时针方向为夹角的正方向,P0~P1为第一段泊车路径,P1~P2为第二段泊车路径,P2~P3为第三段泊车路径,P3~P4为第四段泊车路径,P4~P5为第五段泊车路径.
根据第2节的几何分析, 以路径相关参数l1,l2,l3,R1,R2,θ为变量, 泊车入位为目标, 建立多约束非线性轨迹方程, 其中避障约束为
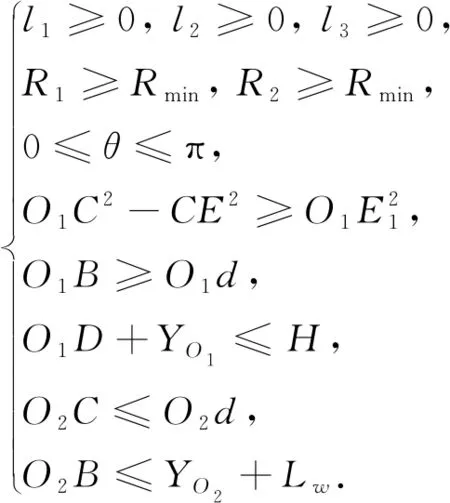
(35)
本文以最小安全车位为目标车位, 其尺寸为 6.4 m×2 m, 车位对面道路宽度H设置为 5.5 m, 依据以上的可行起始泊车区域分析, 选取泊车的起始点坐标, 根据多约束非线性轨迹方程编写MATLAB程序, 求解路径相关参数l1,l2,l3,R1,R2,θ的值.由图 4 可知, 目标车辆从P0点开始泊车, 第一段路径为直线, 方向盘保持回正状态向后倒车, 行驶至P1点后, 将方向盘向右打, 以R1为半径向后倒车, 至车辆后轴中点到达点P2后, 将方向盘向左打至回正状态, 继续向后倒车, 行驶至P3点, 然后将方向盘向左打, 以R2为半径倒车, 当车辆后轴中心点到达P4点后回正方向盘继续倒车, 到达最终泊车位置时, 停止泊车.
5 仿真验证
为了验证该泊车路径规划算法的可行性, 以某SUV车型为例, 建立避障约束条件, 采用解非线性优化问题方法求解各段泊车路径, 在MATLAB上实现了自动平行泊车路径规划算法的编程, 该SUV车的相关参数如表1 所示.
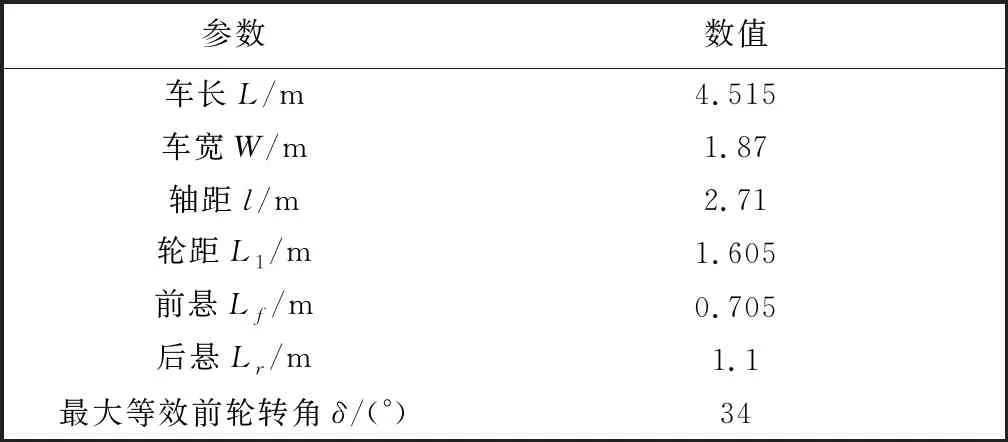
表1 某SUV泊车相关参数
在MATLAB上搭建泊车仿真环境, 其中车位长为6.4 m, 宽为2 m, 泊车通道宽为5.5 m, 仿真车辆的最大泊车速度vm为1m/s, 根据车辆初始泊车状态与车位可能存在的角度进行仿真验证, 车辆初始偏角为-30°, 0°, 30°时的仿真结果分别如图 5 所示.
由图 5 可以看出, 车辆在3种不同初始角度的泊车过程中, 都没有与周围泊车环境发生碰撞, 且成功实现泊车.
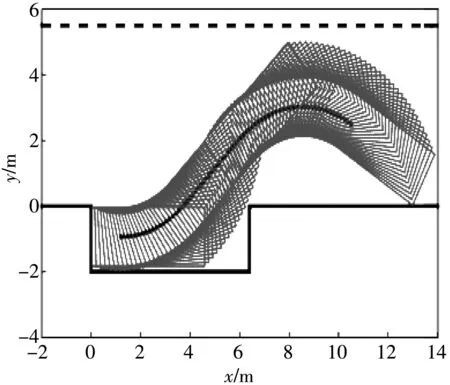
(a) 初始角度为-30°

(b) 初始角度为0°
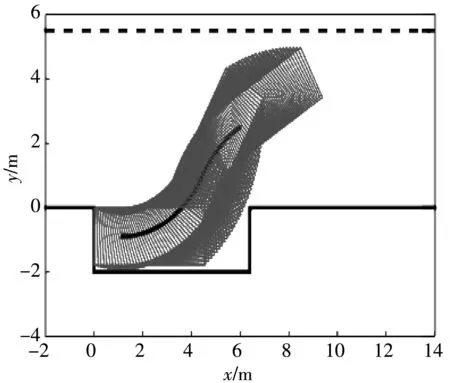
(c) 初始角度为30°
6 结 论
考虑到车辆初始泊车状态与停车位可能存在一定角度, 结合实际的泊车过程, 分析泊车过程中可能产生的碰撞问题, 确定了最小安全车位尺寸, 划分了可行泊车区域, 规划出了一种由圆弧直线组成的五段式平行泊车路径, 该路径可以从实际可能存在的任意初始角度进行平行泊车. 仿真结果表明, 该算法能够从任意初始角度成功生成车辆的平行停车路径, 并能准确地泊车入位.

