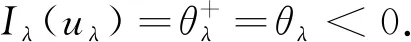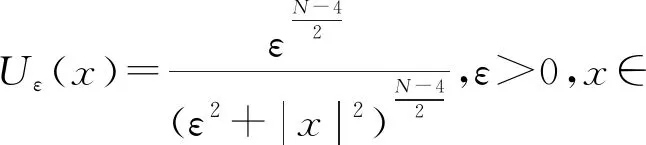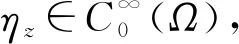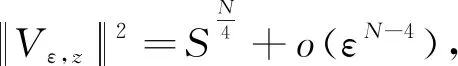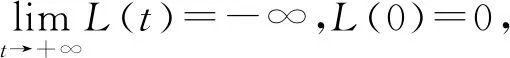具有奇异项的临界重调和方程的多重正解 *
李春平, 桑彦彬
(中北大学 理学院, 山西 太原 030051)
0 引 言
重调和方程产生于研究悬桥周期振动中的行波问题和研究静态偏转的弹性板问题. 近年来, 学者们对重调和方程进行了广泛的研究, 如文献[1] 研究了一类四阶半线性椭圆边值问题的多个非平凡解的存在性; 文献[2-5]获得了具有临界Sobolev指数的双拉普拉氏算子问题解的存在性结果; 文献[6-8]证明了一类Kirchhoff型四阶半线性椭圆边值问题解的存在性; Chen和Li在文献 [9]中讨论了一类四阶椭圆方程, 并获得了解的存在性和多解性的结果. 众所周知, 奇异项的加入使得方程所对应的能量泛函不可微, 导致问题变得困难. 值得注意的是Gaston等在文献[10]中研究了以下奇异重调和方程
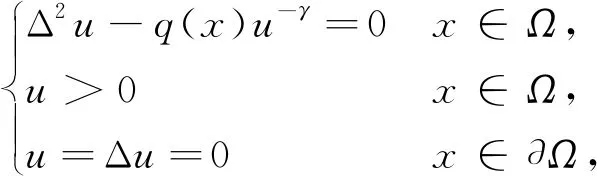
(1)
证明了方程(1)存在唯一的一个正解. 进一步, 由文献[11]的定理1.2, 可得存在唯一的wλ是方程的正解, 且wλ≥cφ1, 其中φ1>0是问题Δφ+λφ=0,φ|∂Ω=0的最小特征值λ1对应的特征函数. 而且不难证明
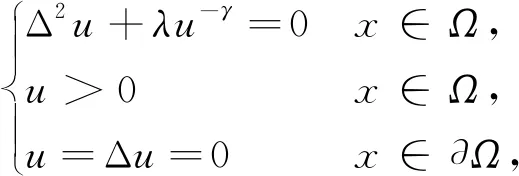
(2)
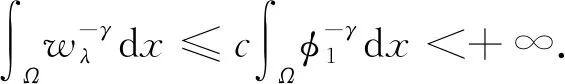
(3)
在本文中, 考虑以下方程
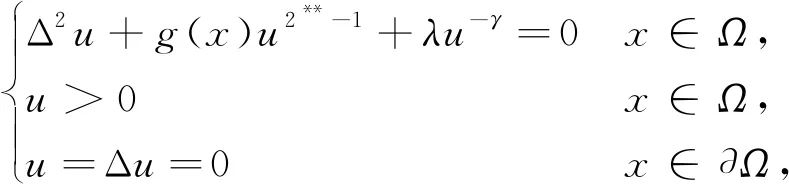
(4)
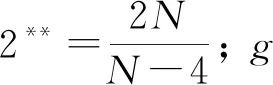
注记1若取g(x)=ex2, 事实上,其满足条件(G).


方程(4)所对应的能量泛函为

为了研究方程(4), 定义f:Ω×R→[0,+∞)为
故将研究方程(4)转化为考虑以下问题
方程(5)所对应的泛函为
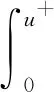
为了克服方程(4)奇异项带来的奇异性, 首先构造了一辅助函数(5), 将奇异问题转化为非奇异问题. 然后, 采用Nehari流形的分解和 Ekeland 变分原理, 通过序列收敛问题得到原问题的解. 本文的创新之处在于对于参数所处区间的上确界进行了精确估计, 便于应用.
1 预备知识和定理(引理)
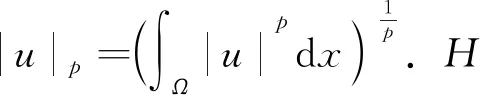
记
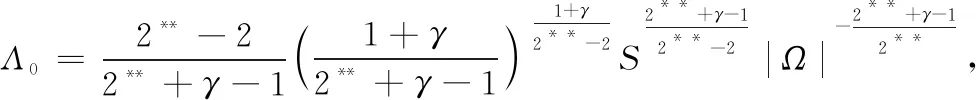
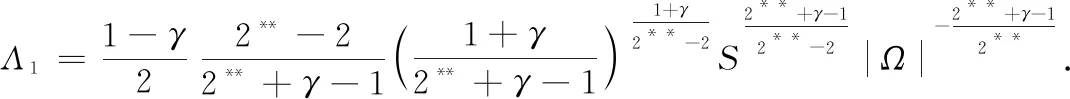
定理1当参数λ∈(0,Λ1), 且g(x)满足条件G时, 方程(4)至少存在两个正解.
引理1对于任意的u∈H,Iλ∈C2(H), 以下结论成立:
1) 若u是Iλ的一个临界点, 则u≥wλ在Ω中几乎处处成立.
2) 若u是Iλ的一个临界点, 则u是方程(4)的一个正解.
证明由于Iλ∈C2(H), 则对于任意的φ∈H,
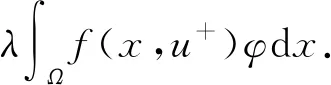
1) 设u是Iλ的一个临界点.选取(u-wλ)-作为试探函数, 则有
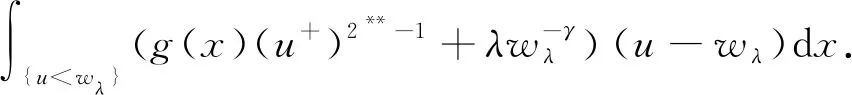
(6)
由wλ的定义可知
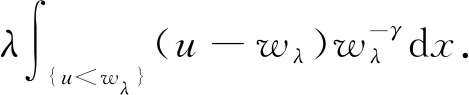
(7)
由式(6)减式(7)可得
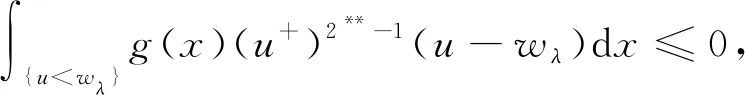

2) 同理可证成立.
基于引理1, 定义H中的闭正锥集合P为
P={u|u∈H,u(x)≥wλ(x), a.e.x∈Ω},
则P是完备空间.
定义Nehari流形为
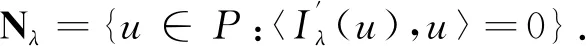
定义hu:t→Iλ(tu),t>0.若u∈P, 有
容易得到

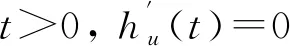

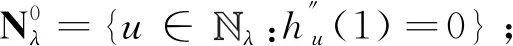
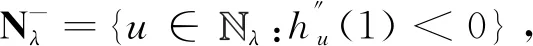
其中
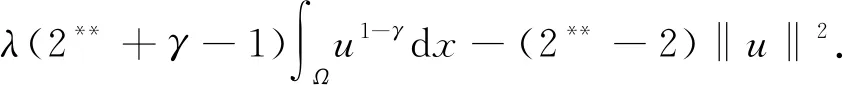
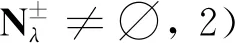

令η′(t)=0, 可得

通过计算可知,η(t)在[0,t0]单调递增, [t0,+∞)单调递减;η(t)在t0处达到最大值.将t0代入η(t), 同时利用Hölder不等式和Sobolev不等式, 以及以下关系式

可得
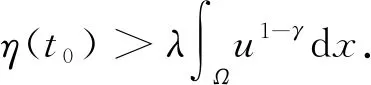
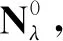

同时由于λ<Λ0, 从而得到

(8)
此外, 由于u∈Nλ, 利用Sobolev不等式可知,

(9)
由文献[12]的引理2.3和引理2.4, 同理可得以下引理.
引理3当参数λ∈(0,Λ0)时, 如果u是Iλ在Nλ上的一个临界点, 那么u是Iλ的一个临界点.
引理4泛函Iλ在Nλ上是强制且下方有界的.
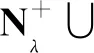

由文献[12]的引理2.5, 引理2.6以及引理2.7, 同理可得以下引理.


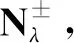
引理7存在一个Iλ的极小化序列{un}⊂Nλ, 对于任意的φ∈H, 使得

vn→v在H和L2**(Ω)中.

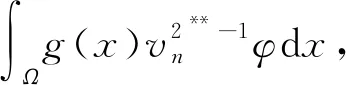
(10)
显然, 此极小序列在H中是有界的, 因此, 存在一个子列, 不妨仍记为{vn}, 使得当n→∞时,



令式(10)的n→∞时, 对于任意的φ∈H,

(11)
令式(11)中的试探函数φ=v, 则可得

(12)
由Brezis-Lieb’s引理(参见文献[13])可知

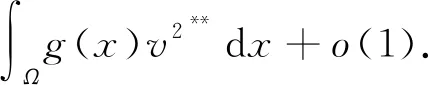
将φ=vn代入式(10)可得

(13)
由式(12)和式(13), 再利用Sobolev不等式
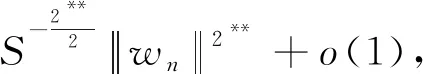
即有


即得到矛盾, 由此可得l=0, 这意味着vn→v在H中, 从而当n→∞时, 有
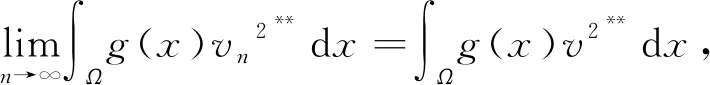
2 定理1的证明
本节对本文主要结果定理1进行证明, 它是下面的引理10和定理2及定理3的直接结果.
定理2若g(x)满足条件G, 方程(4)至少存在一个正基态解.
证明由引理4可知, 存在一个Iλ的极小序列{un}⊂Nλ使得, 当n→∞时
下证uλ是方程(4)的一个基态解. 由引理8可得

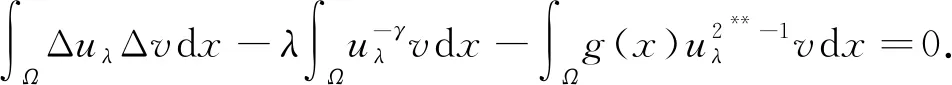
更进一步,

(14)

θλ 再由引理3可知,uλ是方程(4)的一个正基态解, 则证毕. Vε,z(x)=ηzUε,z(x). 当ε→0时, 对于z∈M有 (15) 由文献[13]的引理3.1以及文献[14]可得, 对于z∈M, 以下估计成立 (16) 引理9对于z∈M, 有 证明由于 (17) 又由于uλ是方程(4)的一个正解, 将式(15)~式(17)代入可知, 对于任意的t≥0 而且, 可以推出存在与ε,λ无关的正常数t1,t2, 使得 证毕. 由文献[12]的引理3.3和定理3.4, 同理可得以下引理和定理.