基于驾驶员经验的自动泊车规划算法研究*

胡 文，谭运生，康龙云，于宗光

（1.华南理工大学电力学院，广州 510640； 2.领途汽车有限公司智能驾驶开发部，无锡 214000；3.中国电子科技集团公司第五十八研究所，无锡 214000）

前言

近年来，随着汽车保有量的增加，停车空间越来越小，对驾驶员的操作要求也越来越高，对于经验不足的驾驶员来说，很难轻松地将车泊入拥挤的停车位中。基于这些因素，自动泊车技术得以发展，很多国内外学者开始对其进行研究。

目前，在自动泊车技术领域，国内外学者的研究主要集中在两个方面：（1）路径规划和路径跟踪，首先借助传感器获取泊车可行驶区域，并结合车辆的几何参数，预先规划出一条理想的泊车轨迹，然后设计各种控制器跟踪该泊车轨迹［1-3］；（2）利用先进的控制算法模拟驾驶员操作，分析驾驶员在泊车时用到的经验知识，采用模糊控制、神经网络等先进控制算法［4-6］，进行模拟建模以实现自动泊车。但是，这些算法过于复杂［3-8］，满足不了系统的实时性要求，不利于实际应用。其中，虽然有些算法简单易行，但容易出现曲率不连续问题［9-10］。此外，部分算法［11-13］解决了曲率不连续的问题，但在路径跟踪过程中，需要反馈，计算量较大，对系统的实时性要求高。本文中在考虑算法实时性要求的基础上，借鉴熟练驾驶员的泊车经验，提出了一种简单易行的自动泊车规划算法。

1 问题描述与泊车分析

1.1 问题描述

泊车路径曲率不连续会导致汽车停车原地转向，容易造成轮胎磨损问题。而导致路径曲率不连续问题的原因，大多是在路径规划过程中没有考虑转向盘转向的连续性。本文中在解决该问题时，借鉴熟练驾驶员的泊车经验，对经验驾驶员的泊车过程进行机理分析，并在分析成果的基础上，对该过程进行建模。

1.2 泊车分析

在平行车位的泊车入库过程中，熟练驾驶员的泊车过程可分为6段，即S0、S1、S2、S3、S4、S5，如图1所示，其中，T0、T1、T2、T3、T4为各段之间的连接点。S0段：将车辆行驶至泊车起始点T0，其路径可为直线或曲线，视工况而定；S1段：将车速控制在最小稳定车速vmin，并将转向盘以最大角速度匀速向右打满；S2段：转向盘停留在最右端的位置，提升车速至最大泊车车速vpmax（以减小泊车时间），车辆以最小转弯半径做圆周运动，直至到达一定位置（即点T2）；S3段：降低车速至最小稳定车速vmin，并以最大角速度反方向匀速打满转向盘；S4段：转向盘停留在最左端的位置，提升车速至最大泊车车速vpmax，车辆以最小转弯半径做圆周运动，直至方向角回零；S5段：转向盘快速回正，车辆以最小稳定车速vmin前向、后向行驶，同时适当操作转向盘，将车辆调整至合适的位置与方位。由于本文研究的重点在于泊车入库过程，S0准备阶段和S5回正调整阶段将不对其进行研究。

图1 泊车过程

本文中在参考上述泊车过程的基础上，建立如图2所示的自动泊车控制系统框图。其中，环境信息为环境感知提供的车位信息、可行驶区域信息、车辆位置信息等；泊车控制器根据感知环节提供的环境信息进行自动泊车控制，输出期望转向盘转向角θd和期望车速vd；转向控制器为车辆线控转向控制器，可有效控制转向盘达到目标转向角；速度控制器为车辆速度控制器，通过控制加速和减速使车速稳定在目标车速附近。由于在泊车过程中车速不超过5 km／h，车辆速度较低，可以通过车辆自身的控制器实现目标控制，满足期望的转向盘转向角和车辆速度要求。因此，本文重点在于设计泊车控制器，输入环境信息，输出期望转向盘转向角和期望车速，对速度控制器和转向控制器将不做进一步研究。

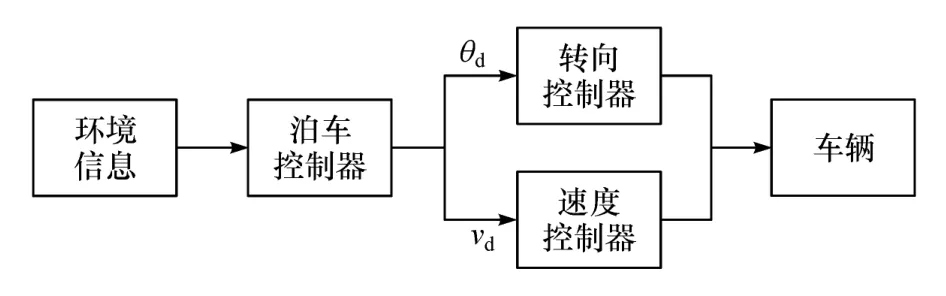
图2 自动泊车控制系统框图

2 控制器建模

如图3所示，去掉S0准备阶段和S5回正结束阶段的泊车过程。其中，LP和WP分别为泊车位长宽；R1和R2分别为S4和S2曲线半径；θ为S4对应的圆周角，也是T3点对应的车辆方向角；ψT为O2T1与纵轴的夹角；Lv和Wv分别为车辆的长宽；L和W分别为车辆的轴距和轮距；Lf和Lr分别为车辆的前悬长和后悬长；Rmin为车辆后轴中点的最小转弯半径。车辆在T0点时的泊车起始位置由后保险杠与泊车位沿x方向的距离D1和车辆右平面与泊车位沿y方向的距离D2确定（见图3）。

由于S2和S4段为转向盘打满后的转向过程，车辆的转弯半径为最小转弯半径。最小转弯半径为：（1）在满足泊车车位最小的情况下，S4段需满足最小转弯半径［14］；（2）在R1取最小值的情况下，R2取值较大时，将使泊车可行区域（D2取值范围）变小，而在Rmin值附近的泊车可行区域最大；（3）从控制难度和精度考虑，R2取最小值（即转向盘打满）的控制难度较低、控制精度较高。

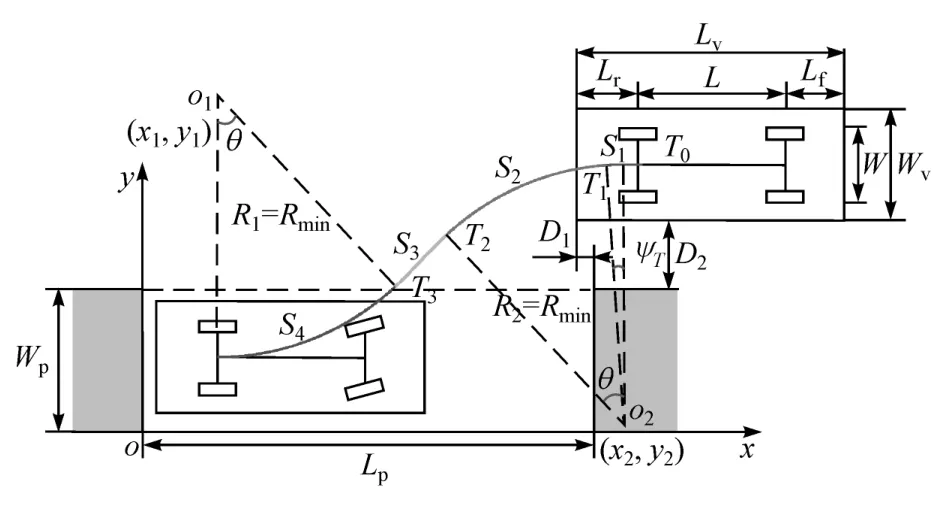
图3 泊车路径规划

S1段为转向盘回正到右打满的过程，S3段为转向盘右打满到左打满的过程，在实际操作过程中可将其看成转向盘匀速转向过程，转向速度为最大角速度。由于S2和S4段转向盘打满不动，车辆行驶轨迹固定，与车速无关。因此，可将S2和S4段的泊车车速提高，以降低泊车时间；而S1和S3段转向盘需要转向，泊车轨迹受车速和转向盘转向影响，为控制泊车精度，可将S1和S3段的泊车车速降低至最小稳定车速。

2.1 转向控制

2.1.1 S1段建模

S1段为转向盘从回正到打满的过程，对S1段的路径进行分析，如图4所示。其中，车辆后轴中心点的起始位置为图示坐标的原点T0，车辆起始方向角为零，并与T0X轴重合；S1为车辆行驶轨迹；T1为轨迹终点；T1Tx为轨迹终点的切线；ψS为T0T1与T0X的夹角；ψT为T1Tx与T0X的夹角，也是车辆方向角。

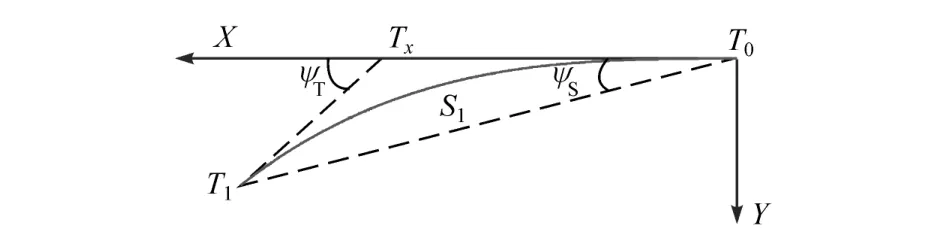
图4 S1段路径轨迹

由车辆运动学关系可得

式中：ψv为车辆横摆角；δf为等效前轮转向角；v为车速；ω为等效前轮转动角速度，可由转向盘角速度ωs和传动比i获取，即ω＝iωs，而与相对应的转向盘转角ηd＝i·δf。

由式（1）可得

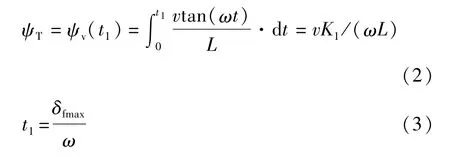
式中：K1＝-log（cos（ωt1））＝-log（cos（δfmax）），K1取值不随时间改变；t1为转向结束时间。

由于泊车过程的速度较低、转向盘转速较快，可在1 s内完成转向盘打满过程，此时的ψv取值较小（在0.05～0.25之间）。因此，可将泊车轨迹S1简化成直线T0T1，sinψv可简化成ψv，同时，泊车轨迹S1可通过车速v乘以时间t1计算，由此可得

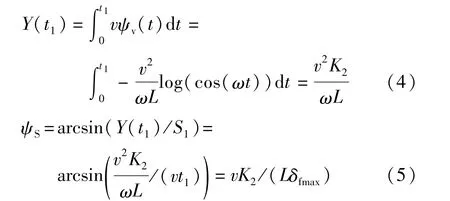
由于K1和K2只与δfmax有关，为降低实际应用中的计算量，提升实时性，可根据δfmax预先计算K1和K2的值。

2.1.2 S3段建模

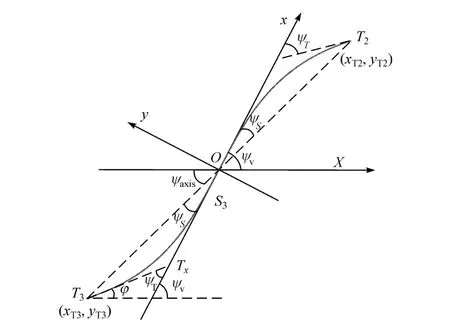
图5 S3段路径轨迹

S3段路径轨迹如图5所示。其中，OX为水平轴，O点为转向盘回正时的坐标点；Ox轴为转向盘回正时的车辆方向，也是S3曲线过O点的切线；T2为轨迹起点；T3为轨迹终点；ψv为车辆在O点时的方向角；ψS为T2T3与Ox的夹角；ψT为过T2和T3点的切线T3Tx与Ox的夹角；φ为过T2或T3点的切线与水平方向的夹角，也是车辆在T2和T3点的方向角；ψaxis为T2T3与Ox的夹角。

由于S3段为转向盘从右打满到左打满的过程，OT2曲线与OT3曲线关于O点点对称，而S3段的前半段可视为S1段的反过程，也即S3曲线的前半段OT2曲线实际上与S1曲线呈镜面对称，因此S3弧长等于S1弧长的两倍。与S1曲线同理，可将S3曲线简化成T2T3直线。同时，基于上述简化条件，可假定ψT和ψS与S1曲线中的值相等，即可由式（2）和式（5）获得。其它需满足的几何关系如下：

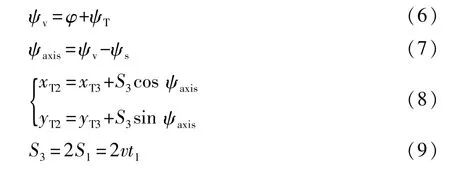
2.1.3 S2段和S4段建模

由前面的叙述和分析可知，S2段曲线为以Rmin为半径的圆弧，如图3所示。因此本节重点须要确定的是本段中车辆的圆周运动应持续的时间，即求车辆到达本段终点T2的时机或位置，为此，取S2弧线在点T2的半径线与纵坐标的夹角θ为待求的变量。

由几何关系可得

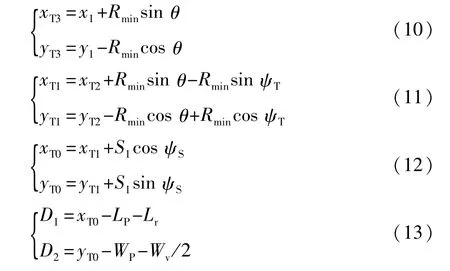
结合式（6）～式（13），可得

在车辆的速度v和转向盘角速度ωs固定的情况，式（13）中的S1、ψT和ψS为固定值，在D2已知的情况下，可由式（14）求得θ值。借助Mathematica软件的推导可得

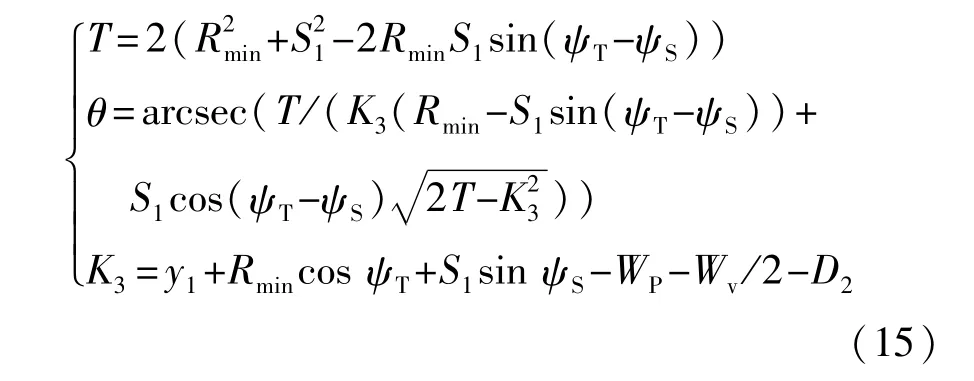
由于ψT和ψS数值较小，式（15）中的sinψS≈ψS，sin（ψT-ψS）≈ψT-ψS、cos（ψT-ψS）≈1，式（15）可进一步简化为

至于S4段，它与S2段类似，不再存在待求的未知量，在此无须赘述。

2.1.4 路径约束

现对车辆在泊车过程中可能发生的碰撞情况进行分析，如图6所示，为保证泊车过程中的安全，设定一些安全距离：Df，Dr，Di，Do和Drb。

（1）根据汽车车身顶点D的碰撞分析，可确定泊车位的宽度WP。如图6所示，在S4段的D点圆弧半径为

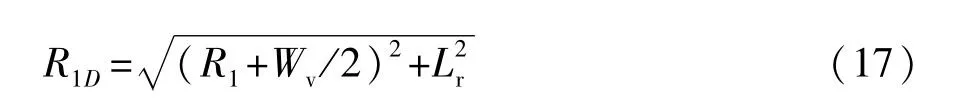
图6 泊车路径约束示意图

车位宽度WP为

式中WPmin为最小车位宽度。

（2）根据汽车车身顶点C的碰撞分析，可确定泊车位的长度LP。如图6所示，在S4段的C点圆弧半径为

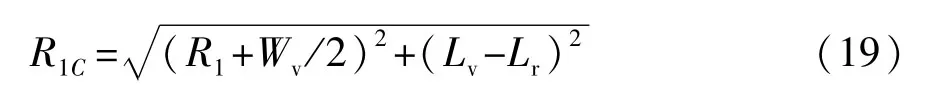
车位长度LP为

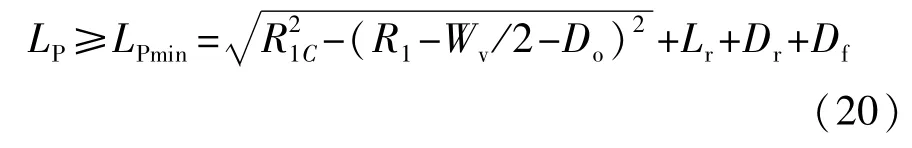
式中LPmin为最小车位长度。

（3）根据汽车车身顶点B与泊车位另一侧障碍物的碰撞分析，可确定泊车空间所需的宽度H。由于S1段的侧向位移较小，为方便计算，对B点的运动轨迹进行简化，如图6所示，简化后的B点圆弧半径为

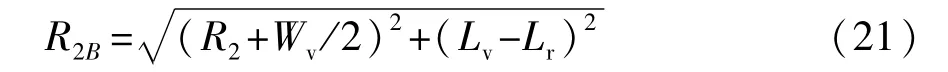
泊车空间宽度H为

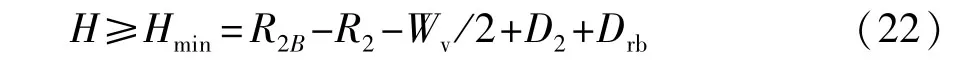
式中Hmin为泊车空间宽度。

（4）车辆在S2段的泊车过程中，可能会与泊车位顶点B′发生碰撞，最可能的碰撞点为车身E点，E点为后轴延长线与车身侧边的交点。如图6所示，只有在O2点的坐标x2＞LP时，才会发生碰撞，因此可得以下几何关系：

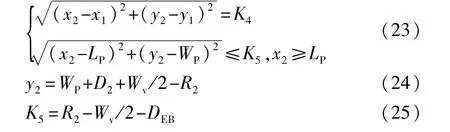
式中：DEB为E点至B′点的安全距离；K4为圆心O1与O2的距离。结合图7中的几何关系可得

图7 圆心O1与O2距离示意图

2.1.5 泊车位置

在泊车信息已知的情况下，可根据上节中的路径约束条件，计算得到泊车起始位置D1和D2的范围。

由于在泊车转向过程中的车速v和转向角速度ωs事前设定，S1、ψT和ψS可提前求得，而R1和R2采用最小半径Rmin。因此，可由式（22）求得D2的最大值：

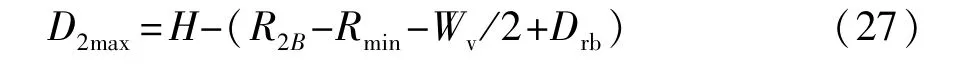
由式（23）～式（26）求得D2的最小值：

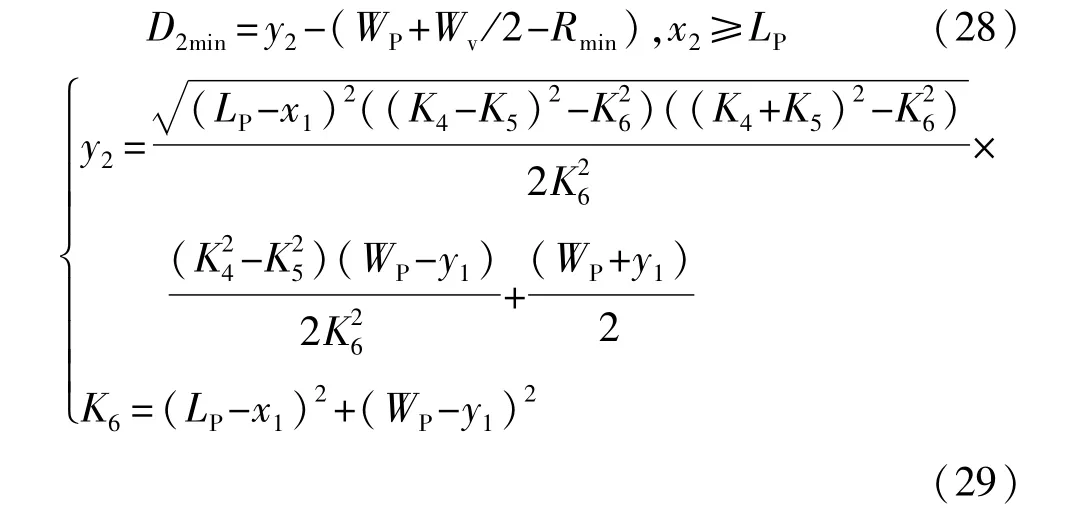
其中，上式中的O1点坐标（x1，y1）可由图6所示的几何关系得到

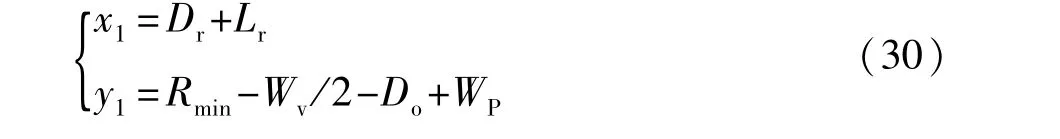
而当x2＜LP时，车辆侧向CD边应与车位边A′B′保持DEB的安全距离，即

结合式（28）和式（31）可得D2的最小值：

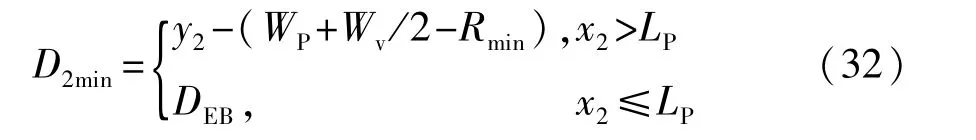
在D2已知的情况下，可以根据式（23）和式（24）求得D1的情况：

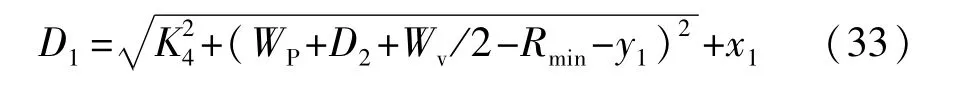
此外，后轴的最小转弯半径Rmin和前轮等效转角δfmax可由车辆几何关系求得

对于熟练驾驶员来说，在泊车之前会将车停在熟悉的泊车区域，即由D1和D2确定的区域。而大多数驾驶员的侧向区域D2的范围为0.4～1.0 m，这是由于侧向距离D2较小可以缩短停车时间，同时，也方便给另一侧留有更多的可行空间，便于他人行走。为此，在实际应用中，当泊车系统自动寻找车位时，可将车停在靠近车位的位置，即D2的可行区域为0.5～1.0 m范围内。

2.2 速度控制

参考熟练驾驶员的驾驶经验，在车辆转向盘转动的过程中，将车速控制在最小稳定车速vmin；在转向盘稳定过程中，将车速提升至最高泊车车速vmax，一般在5 km／h左右。为此可得如图8所示的车速控制过程。

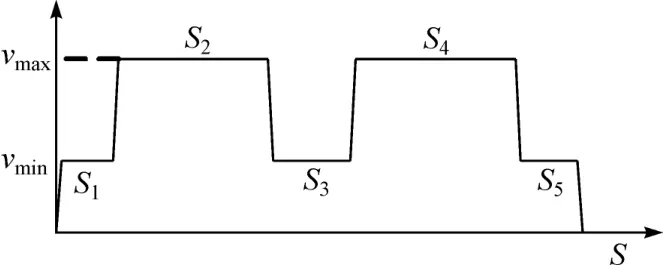
图8 车速控制过程

2.3 控制流程

上文对泊车控制的转向控制和速度控制进行了分析，现将泊车控制器的整个控制流程进行归纳。其中，由于车辆的几何参数、最小稳定车速vmin、转向盘最大稳定转速已知且安全距离预先设定，由此可计算得到S1、ψT、ψS、K1、K2、K4和K5等信息，泊车控制器可预存这些控制信息，便于减少重复计算量。

泊车前的参考计算过程如下：

（1）首先将车辆停在D2可行区域内，同时，感知系统进行泊车空间探测；

（2）判断泊车空间是否满足LPmin和WPmin，不满足则提示信息并退出泊车过程；

（3）判断泊车位置是否满足D2min和D2max，不满足则提示信息并退出泊车过程；

（4）根据D2计算θ、D1和T2的横坐标xT2。

3 仿真结果

为验证泊车算法的可行性，本文中以天津一汽夏利N5车型为例，利用Matlab／Simnlink建立本文提出的规划算法，并结合泊车过程中的极限和正常工况，对算法进行验证，参数如表1所示。选择车位尺寸LP×WP为7 m×2.4 m，道路宽度H为4 m，车辆的最低稳定车速vmin为2km／h，最大泊车车速vpmax为5 km／h。不同车辆的最低稳定车速和最大泊车车速有所不同，可根据实际情况标定获得，这里仅作参考。根据车辆相对车位的不同侧向距离D2，选择3种泊车情况进行分析。

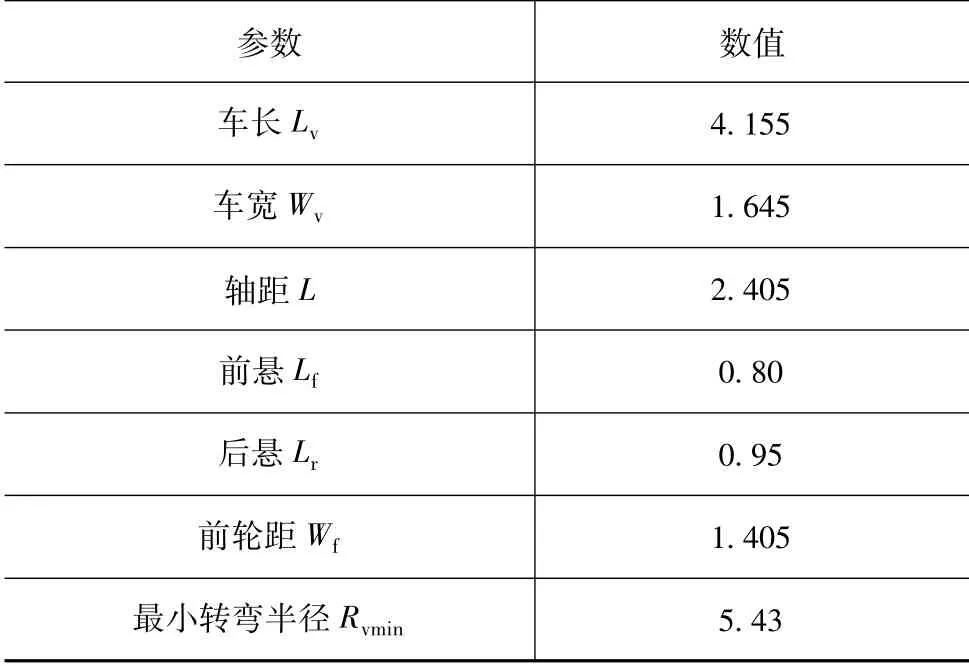
表1 乘用车与泊车有关的主要参数 m

为显性验证控制器满足碰撞约束条件的有效性，现将各安全距离均设为0，进行研究分析。如图9所示，在泊车侧向距离D2取最小值时，在泊车过程中，车辆侧向与车位之间的最小间隙DEB为0.003 m，车辆后侧与车位之间的最小间隙Dr为-0.003 m。造成误差的原因在于为提高实时性，对算法进行了部分简化处理。同时，如图10所示，在泊车侧向距离D2取最大值时，在泊车过程中，车辆侧向与障碍物之间的最小间隙Drb几乎为0。由此可见，本文中设计的泊车控制器误差非常小，能对车辆进行精确无误的控制。

图9 D2为D min的仿真结果

图10 D2为D max的仿真结果

此外，为结合实际泊车过程中的情况，将算法中的安全距离Df、Dr、Di、Do、Drb和DEB设为0.2 m，将Dr设为0.4 m，确保泊车安全并再次进行仿真分析。如图11所示，本文中设计的泊车控制器能使车辆精确、无碰撞地泊在设计的泊车终点区域内，且能获得比较理想的泊车效果。同时，如图12所示，转向盘在转向过程中，车速控制在2 km／h；转向盘打满后，车速迅速提升至5 km／h；整个泊车过程时间不足7 s。由此可见，本文中设计的控制器与熟练驾驶员的驾驶经验一致，在对车速进行变速控制的同时，既满足了精度需求，又有效控制了泊车时间。

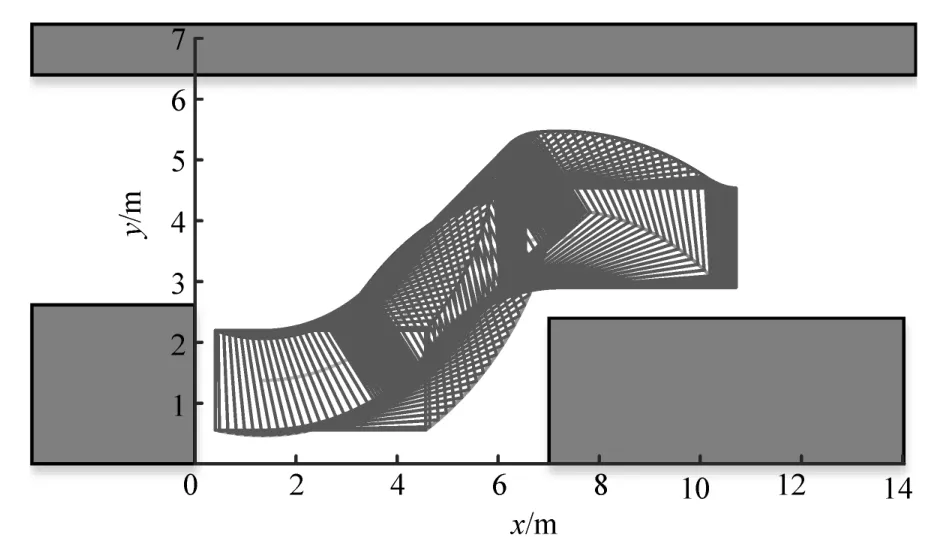
图11 D2为0.5 m的仿真结果

图12 D2为0.5 m时的转向盘转角和车速变化过程

为进一步研究，现将本文中所提算法与其他泊车算法（B算法）进行对比。B算法主要通过控制车辆横摆角从0°-45°-0°，从而实现平行车位的自动泊车，如图13所示。为方便对比，泊车终止点和各安全距离与图11的仿真条件保持一致。

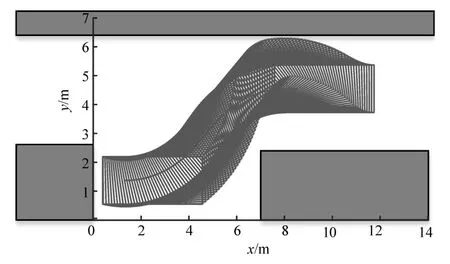
图13 D2为D min（B算法）的仿真结果

从图13和图11可以看出，在D2取Dmin时，其泊车轨迹离上边沿只有0.1 m，并不满足0.2 m的要求，这说明该算法对泊车空间有更高的要求，降低其实用性。同时，在泊车终止点相同的情况下，该算法所需最小侧向距离Dmin为2.155 m，而本文中所提算法最小侧向距离Dmin＝DEB，即只需要0.2 m，这说明本文中所提算法对泊车空间要求较小，更容易在狭窄的环境中实现泊车。此外，从图14可以看出，其泊车时间较长，完成泊车需要8.1 s，大于本文的算法6.8 s，若采取提高泊车速度来缩短泊车时间，这将进一步提升对泊车空间的要求，导致泊车空间不足。

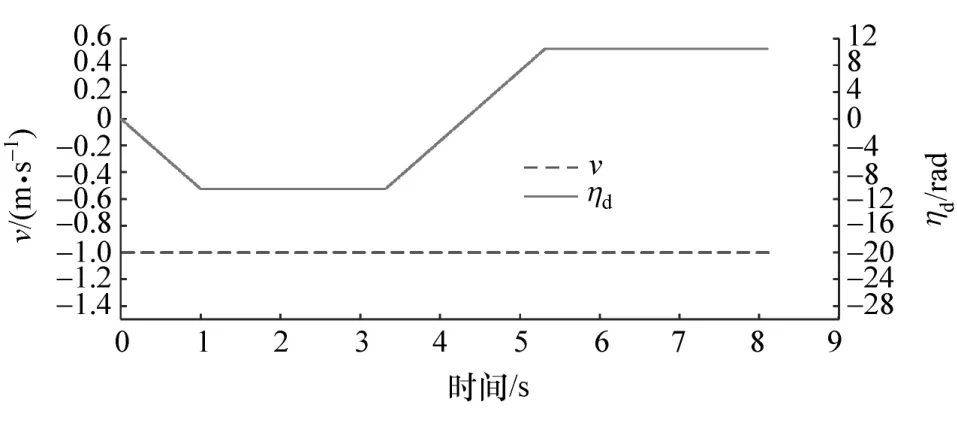
图14 D2为D min（B算法）的转向盘转角和车速变化过程

综合以上的仿真结果可以看出，本文中所提算法在不牺牲精度的情况下，减少了运算量，进而减轻对泊车系统的性能要求，实用性更强。同时在泊车过程中，对速度进行控制，进一步减少了对泊车空间的要求。

4 结论

（1）为解决泊车过程中曲率非连续问题，避免原地转向，本文中借鉴熟练驾驶员的驾驶经验，对其过程进行分析，由此提出了一种基于驾驶员经验的自动泊车规划算法。该算法主要基于驾驶员经验对泊车路径进行规划研究，并对泊车过程中各个阶段和可能发生的碰撞情况进行建模分析，并由此推导出泊车区域的要求。

（2）利用Matlab／Simulink搭建所提出的规划算法，并结合泊车过程中的极限和正常工况，对算法进行验证。仿真结果表明：本文中提出的算法能实现精确的自动泊车控制；算法的部分简化对控制器控制精度影响较小，简化结果行之有效；控制器中的速度控制，既能满足精度要求，又能达到泊车时间要求，与预期设计思路一致。

（3）本文中解决的是一般工况下的自动泊车问题，对于一些特殊工况下的自动泊车问题未必适用，比如车辆前方有障碍物致使泊车可行区域D2不满足要求。因此，为应对各工况下的自动泊车问题，后续研究中将在优化本文算法的同时，着手解决特殊工况下的自动泊车问题。