考虑轮齿修形的变厚齿轮啮合刚度数值计算

毛汉成 ，傅 琳，于广滨，+，Tupolev Valerii，，刘 伟

(1.哈尔滨理工大学 机械动力工程学院，黑龙江 哈尔滨 150080；2.哈尔滨工业大学 机电工程学院，黑龙江 哈尔滨 150001；3.中国船舶重工集团公司第七○三研究所，黑龙江 哈尔滨 150078)

0 引言

渐开线变厚齿轮为一种新型齿轮形式，其变位系数沿轴线方向呈线性变化，通过调整轴向位移可以调整变厚齿轮副的啮合间隙，而且因为变厚齿轮具有结构简单、加工方便、加工成本低的特点，所以变厚齿副被广泛应用于四驱汽车分动器与高速小倾角船用齿轮箱等领域。然而，在变厚齿轮的实际啮合传动过程中，啮合刚度时变性所导致的系统振动不可避免，相比传统渐开线齿轮，变厚齿轮不同截端面上的齿顶圆、齿根圆、压力角数值均不同，其轮齿间接触状态相比传统渐开线齿轮更加复杂。因此，研究变厚齿轮的时变啮合参数有利于改善啮合特性，对提高其传动平稳性具有十分重要的意义。

目前通常采用材料力学法、弹性力学法、有限元法和试验法计算齿轮时变啮合刚度，其中有限元法和材料力学法相对常用而且方便、有效[1-2]。对于材料力学法，目前主要的理论依据为Weber能量法。国外CORNEL[3]和OSWALD等[4]基于Weber法，运用数值积分求解渐开线直齿轮啮合刚度；国内颜海燕等[5]对基于Weber 能量法的数值积分公式进行了详细推导，并编制了计算程序；张奎晓等[6]在Weber能量法的基础上引入基体变形因子，提出基于齿轮加工工艺的渐开线齿轮精确建模方程；杨长辉等[7]采用变增量法确定了齿轮啮合点和法向载荷，并采用Weber能量法计算出了某大功率风电齿轮箱一级行星轮直齿轮时变啮合刚度；万志国等[8]通过建立考虑齿根圆修正的齿轮裂纹变截面悬臂梁模型，明显提高了Weber能量法在齿轮时变啮合刚度上的求解精度。对于复杂齿面时变啮合刚度的计算，近年有学者通过曲面积分与有限元仿真相结合的方法对准双曲面齿轮进行齿轮加载接触分析(Loaded Tooth Contact Analysis，LTCA)，从而计算齿轮的时变啮合参数[9-10]。韦乐余等[11]基于有限元加载接触分析原理，结合谐波齿轮的静态和动态接触特点,得到了谐波齿轮单齿刚度曲线和综合啮合刚度曲线；陈晓霞等[12]提出一种基于空载侧隙和周向线性啮合刚度的理论迭代算法，用于计算随负载变化的负载侧隙和啮合力分布；李学艺等[13]提出一种基于滚切加工原理的齿轮精确建模及啮合仿真分析方法，实现了齿轮的参数化精确建模与瞬态啮合分析；刘鹏等[14]通过有限元法研究微线段齿轮的时变啮合刚度，并总结出微线段齿轮特殊参数对其啮合刚度的影响规律。

综上所述，目前有限元方法常被用来处理复杂齿面的接触问题，而且复杂齿面的时变啮合刚度可以通过轮齿的弯曲、剪切等变形来计算，然而有限元方法建模十分繁琐，分析计算耗时较长，并且有限元模型的网格精度会严重影响计算结果的准确性。因此，目前迫切需要一种有效求解变厚齿轮啮合刚度的方法。本文针对传统Weber能量法进行改进，在综合考虑变厚齿轮基圆与齿根圆之间关系的基础上，基于分片法提出一种考虑轮齿修形的变厚齿轮时变啮合刚度求解模型，并采用MATLAB编写程序进行数值计算。在此基础上采用集中参数法分析不同啮合参数对其轮齿综合啮合刚度的影响规律，为变厚齿轮的结构优化设计和系统动力学分析奠定基础。

1 考虑轮齿修形的变厚齿轮啮合刚度数值积分公式推导

1.1 考虑修形的变厚齿轮齿廓方程

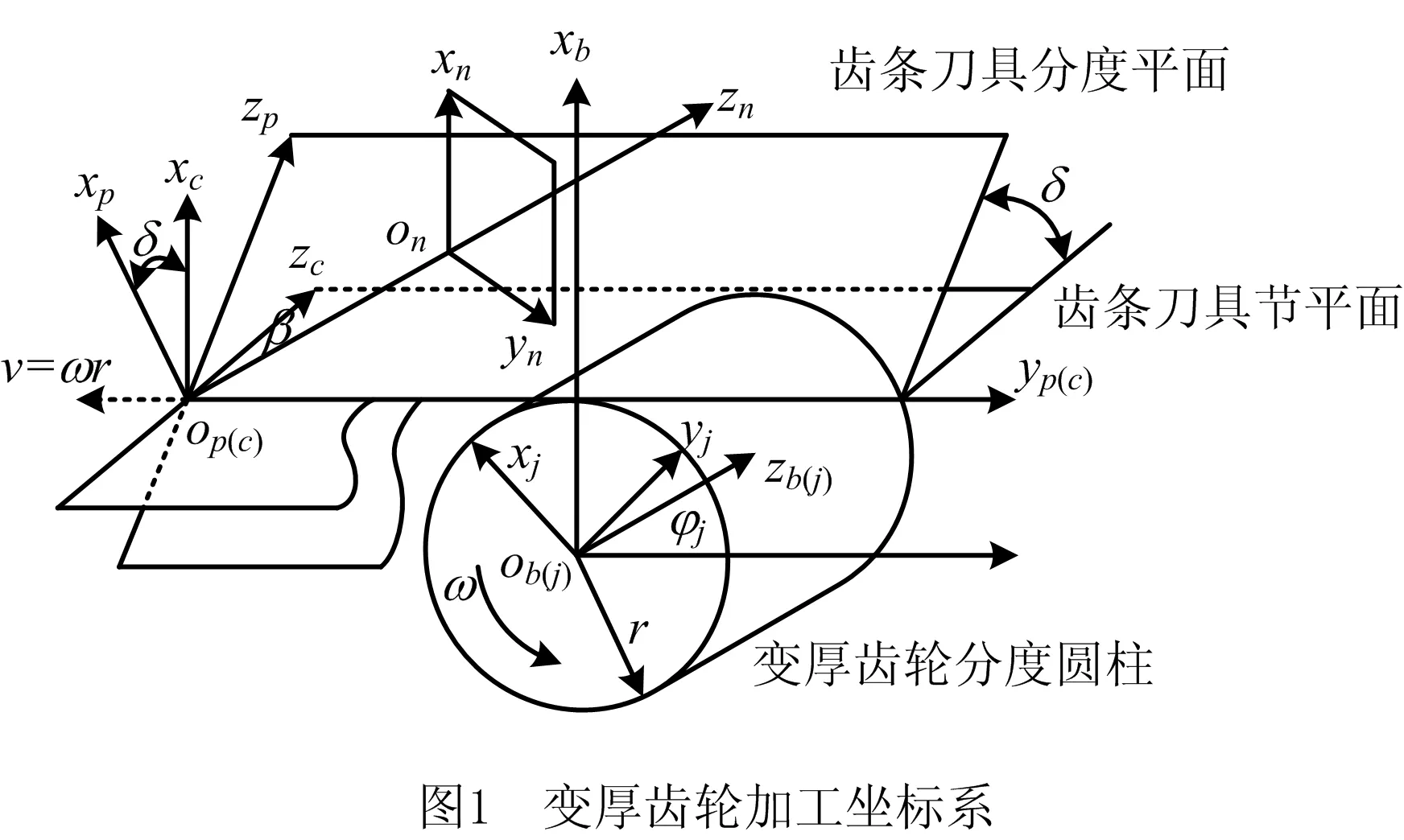
根据MITOME[15]的变厚齿轮齿面生成理论，齿条刀具的分度平面与被切齿轮平度圆柱平面的夹角为δ，两者的相对运动与加工直齿圆柱齿轮一样，即齿轮毛坯与齿条刀具的节平面相切作纯滚动，建立如图1所示的坐标系，其中：Sn=(On_xnynzn)，Sp=(Op_xpypzp)，Sc=(Oc_xcyczc)分别为与齿条加工刀具法面、端面和节面固联的坐标系；Sj=(Oj_xjyjzj)为与齿轮毛坯固联的动坐标系；Sb=(Ob_xbybzb)为空间固定坐标系；法面坐标系与端面坐标系所成的角度为螺旋角β，端面坐标系与节面坐标系所成的角度为节锥角δ；ω为齿轮毛坯回转角速度，φ为旋转角度，r为预加工变厚齿轮分度圆半径，则齿条刀具加工移动速度v=ωr。

通过渐开线变厚齿轮加工过程进行坐标变换，坐标变换顺序依次为Sn→Sp→Sc→Sb→Sj，最终得到坐标系Sj=(Oj_xjyjzj)下的渐开线变厚齿轮齿面方程[16]

(1)

式中：xc，yc，zc为齿条刀具齿面在坐标系Sc中的位置矢量；nxc，nyc，nzc为齿条刀具齿面在坐标系Sc中的单位矢量。

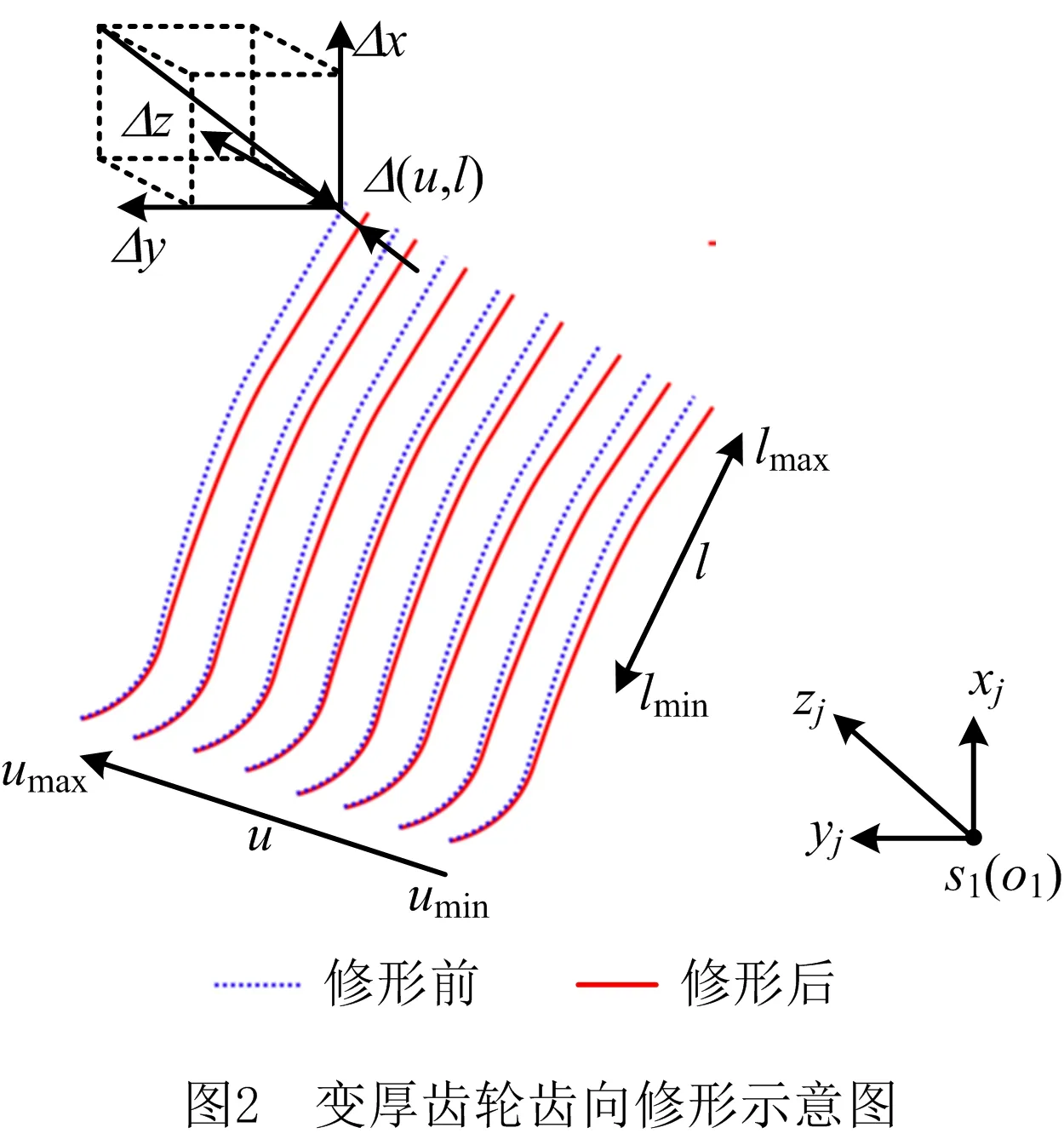
图2所示为渐开线变厚齿轮修形示意图，其中Δu为修形量。将修行量Δu分解到坐标系Sj=(Oj_xjyjzj)沿x，y，z的分量Δx，Δy，Δz，建立包含修形参数的渐开线变厚齿轮齿面方程

(2)

(3)

1.2 基于分片思想构建变厚齿轮啮合刚度计算模型

对于普通渐开线圆柱齿轮，其瞬时接触线平行于齿轮轴线，单位齿宽上任意啮合点的齿廓半径和法向啮合力均一致。因此，轮齿齿面在法向啮合力Fk作用下的单位齿宽上任意啮合点j处的轮齿啮合综合刚度k可表示为

(4)

式中：B为齿宽；δk为齿轮轮齿任意啮合点j处在法向啮合力Fk作用下产生的弹性变形，主要由轮齿的弯曲及剪切变形δbk、齿根弹性引起的附加变形δfk和齿面啮合的接触变形δhk3部分组成；k1，k2分别为主、从动轮轮齿在啮合点j处的法向啮合刚度。

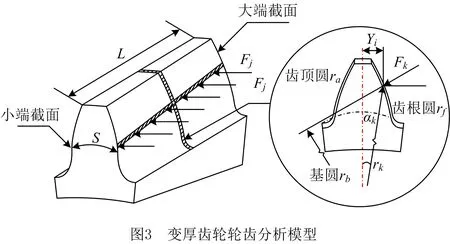
对于渐开线变厚齿轮，因为变位系数沿轴线方向呈线性变化，其端截面方向可以看作由无限个无限薄且具有不同变位系数的直齿轮连续叠加而成，同一时刻，单位齿宽上任意啮合点的齿廓半径和法向啮合力均不同，所以本文采用分片法对变厚齿轮轮齿齿面时变啮合刚度进行计算。如图3所示，将变厚齿轮轮齿沿轴向方向切分为若干个厚度相同的薄片齿轮，通过确定每一薄片轮齿的啮合点位置和法向载荷计算轮齿瞬时接触点的变形柔度。在不考虑齿廓偏差的情况下，变厚齿轮副任意啮合点j处的总刚度等于处于啮合中的各薄片轮齿副的刚度之和，即

(5)

1.3 基于Weber能量法的变厚齿轮啮合刚度改进算法

本文在材料力学的理论基础上，综合文献[5-7]轮齿啮合综合刚度计算公式的推导，以小倾角船用齿轮箱中相交轴变厚齿轮副为研究对象，将其轮齿简化为沿齿宽方向呈线性变化的变截面悬臂梁，通过将轮齿有效接触部分微分为一系列微元，将每一个微元计算所得的弹性变形进行叠加，求得任意瞬时啮合点处的法向变形柔度。另外，因为渐开线变厚齿轮轴向变位系数呈线性变化，轴向各端截面齿形参数均不同，所以本文通过对渐开线变厚齿轮沿齿宽方向进行离散化，分析讨论齿轮基圆与齿根圆大小关系对轮齿啮合刚度的影响，并对传统Weber能量法进行改进，以提高渐开线变厚齿轮时变啮合刚度的求解精度。

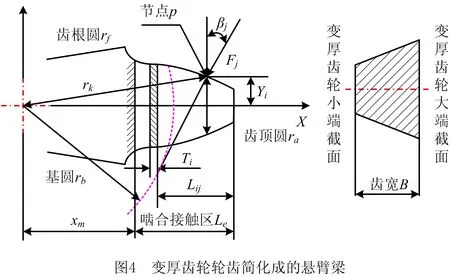
1.3.1 基圆半径小于齿根圆半径时的参数描述

当齿轮基圆半径小于齿根圆时，传统Weber能量法所简化的悬臂梁长度大于实际工况，所计算的轮齿变形包含了齿轮基圆与齿根圆之间的部分变形，因此所得的啮合刚度结果偏小。

将齿轮沿齿廓方向分为k个啮合点，每个啮合点对应的半径为rk，

(6)

当齿轮基圆半径小于齿根圆时，整个齿都视为渐开线齿廓，有：

(7)

式中：xk为任意啮合点j距离齿轮圆心的距离；r1为齿轮的分度圆半径；Ti为微元长度；yib，yis分别为任意啮合点j处的大端和小端端面半齿厚。

1.3.2 基圆半径大于齿根圆半径时的参数描述

当齿轮基圆半径大于齿根圆时，传统Weber方法所简化的悬臂梁长度小于实际工况，因为未考虑齿轮基圆与齿根圆之间的部分变形，所以传统Weber方法计算的轮齿变形偏小，所得啮合刚度结果偏大。当基圆大于齿根圆时，将基圆到齿根圆部分视为矩形，变厚齿轮大端、小端的矩形宽分别为Sb1，Sb2，有：

(8)

(1)当任意啮合点k处的半径小于基圆半径，即rk≤rb时，

yib=0.5Sb1，yis=0.5Sb2。

(9)

(2)当任意啮合点k处的半径大于基圆半径，即rk>rb时，

(10)

1.4 基于Weber能量法的变厚齿轮啮合刚度改进算法

1.4.1 弯曲和剪切变形

将变厚齿轮沿齿宽方向分为N份薄片齿轮，每份薄片齿轮的厚度为L/N，任意薄片齿轮的受力等效图如图5所示，齿轮单齿弯曲和剪切总变形量δbj由每一个微元i的变形叠加得到。每个微元被认为是左端固定，而且每个微元右端面相连的部分可视为刚体，因此第m片薄片齿轮的单齿弯曲和剪切总变形量

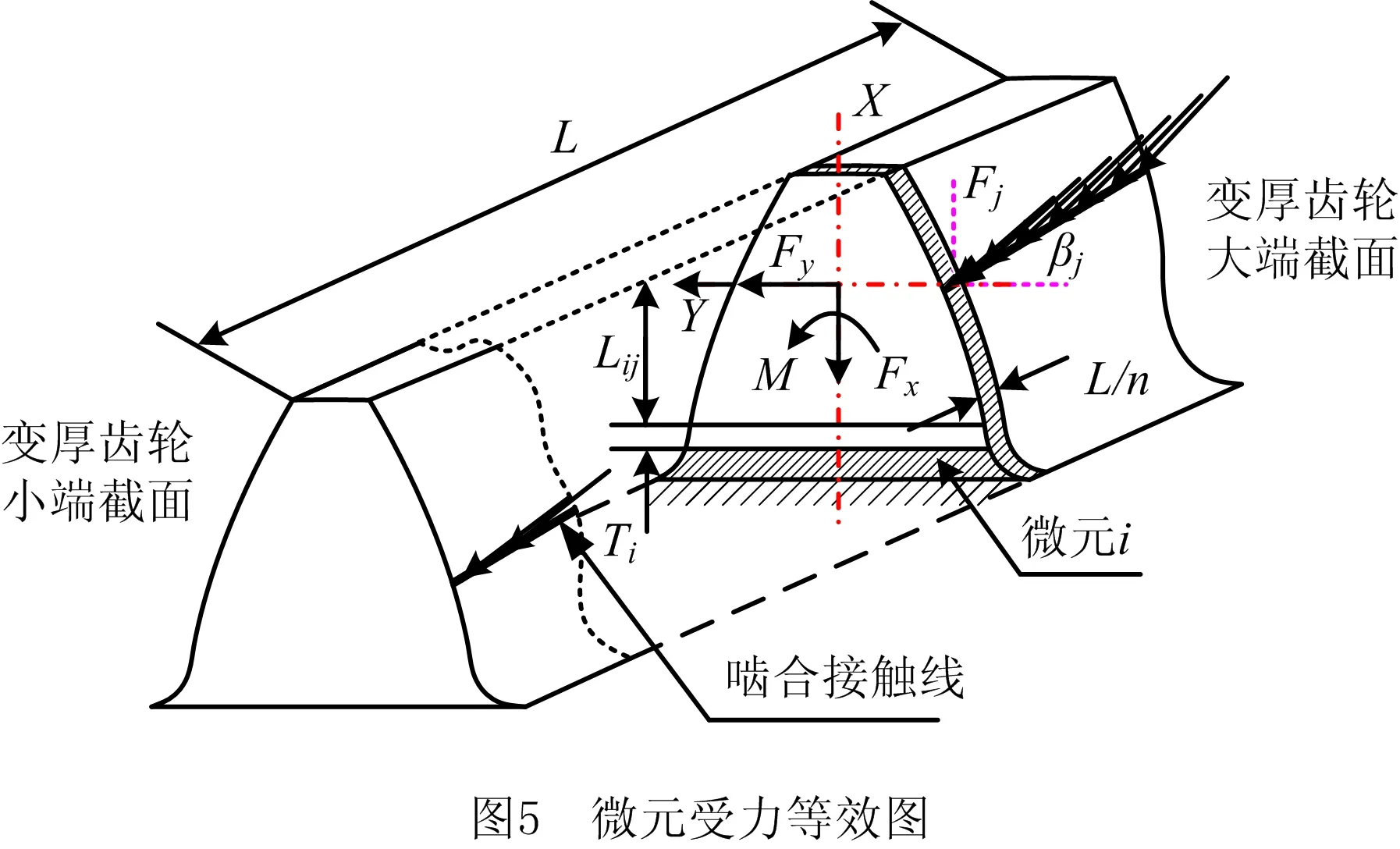
式中：n为有效啮合区内微元i的总数；δbj为微元i在法向啮合力Fj作用下产生的变形。微元i的变形主要包括Fx作用下产生的压缩变形，Fy和M共同作用下产生的弯曲变形，Fy作用下产生的剪切变形3部分。

另外，第m片薄片齿轮轮齿X轴方向上的受力为

齿轮轮齿Y轴方向上的受力为

齿轮轮齿所受的等效弯矩为

Fx作用下产生的压缩变形为

(11)

Fy作用下产生的扰度为

(12)

Fy作用下产生的转角为

(13)

M作用下产生的扰度为

(14)

M作用下产生的转角为

(15)

轮齿的弯曲变形为

δmi=ω1+θ1Lij+ω2+θ2Lij。

(16)

将式(12)～式(15)代入式(16)，得薄片变厚齿轮轮齿受载荷Fj作用在小段i上的弯矩引起的变形

(17)

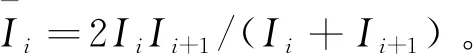
轮齿的剪切变形为

(18)

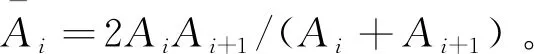
因为渐开线变厚齿轮轮齿有效接触部分系列微元的轴向可视为梯形变截面，所以

(19)

(20)

式中：Sib，Sis分别为微元i在变厚齿轮大端截面和小端截面的齿厚(单位：mm)。

因此，轮齿齿部在载荷Fj作用点处沿载荷方向的总变形

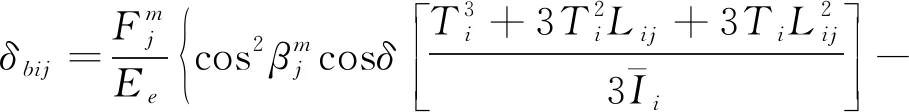
(21)

1.4.2 变厚齿轮齿根(基础)弹性引起的附加变形

根据Cornell，将变厚齿轮轮齿的根部看作为弹性的轮缘，变厚齿轮齿根弹性引起的附加变形量计算方法如下：

(1)对于窄齿，有

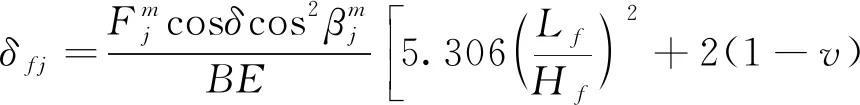
(22)

(2)对于宽齿，有

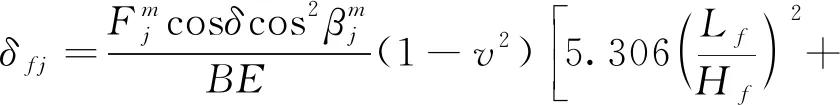
(23)

根据有效长度Le，可以求出

Hf=2YM。

1.4.3 变厚齿轮齿面啮合点的接触变形

根据文献[18]的计算公式，任意啮合点j处的局部接触变形为

(24)

1.5 变厚齿轮综合啮合刚度计算公式

综上所述，第m片薄片变厚齿轮副的综合变形为

(25)

第m片薄片变厚齿轮单位齿宽上任意啮合点j处的啮合刚度为

(26)

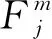
因此，渐开线变厚齿轮总啮合刚度为

(27)

2 数值计算结果分析与验证

2.1 变厚齿轮轮齿时变啮合刚度数值的计算

本节通过MATLAB编制程序，并进行数值计算，计算流程如图6所示。

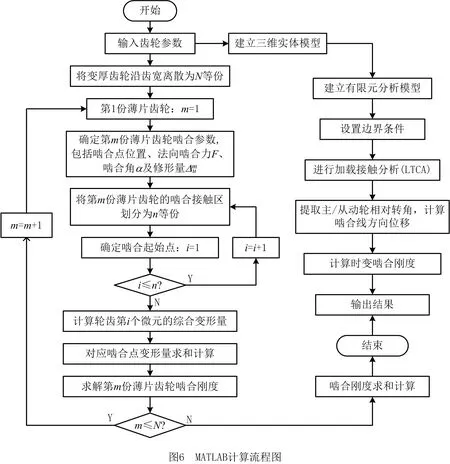
(1)输入变厚齿轮参数，具体如表1所示，设置输入扭矩为70 N·m。

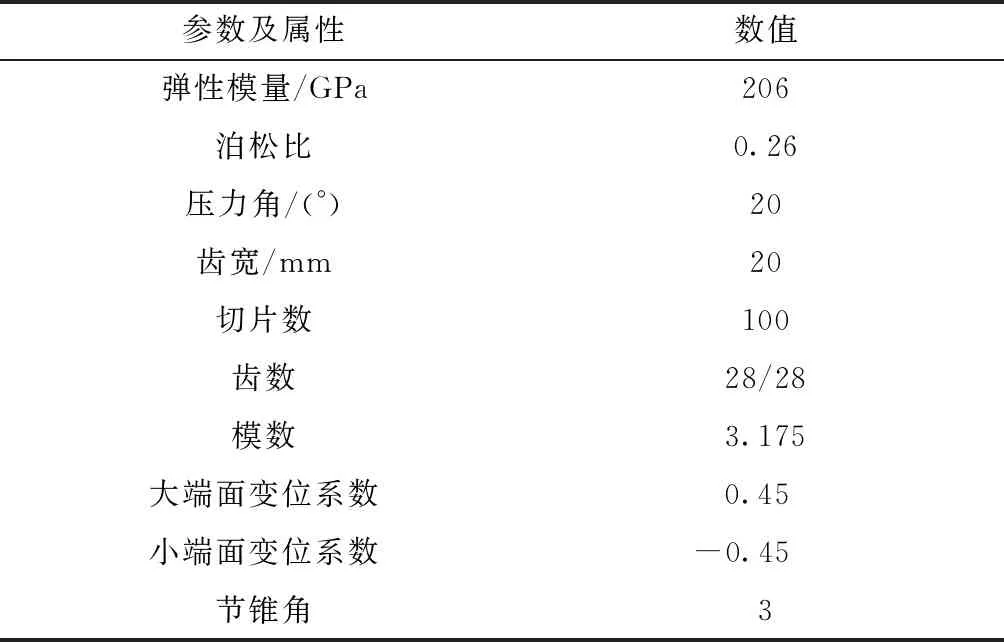
表1 齿轮几何参数及材料属性

(2)将变厚齿轮沿齿宽方向离散N等份。

(3)确定第m份薄片齿轮的啮合参数，包括初始啮合位置、法向啮合力和啮合角。

(4)将第m份薄片齿轮啮合区域划分为n个微元。

(5)求解每个微元i的综合变形。

(6)计算第m份变厚齿轮轮齿的综合变形，求解轮齿啮合综合刚度。

(7)对N等份薄片齿轮啮合综合刚度进行求和，并输出结果。

2.2 轮齿综合变形计算结果分析及啮合刚度计算

根据上述理论方法，通过MATLAB编制程序，参照图6计算流程对变厚齿轮啮合刚度进行计算。为便于与现有文献进行对比分析，本文将节锥角δ分别设置为0°和3°。如图7所示，节锥角δ=0°齿轮(即为传统渐开线齿轮)轮齿综合变形计算结果与文献[4]的计算结果相比，由于本文方法增加了齿轮基圆与齿根圆之间的部分变形，相比传统Weber方法，本文计算的轮齿变形量偏大，最大变形偏差量为1.85 μm。

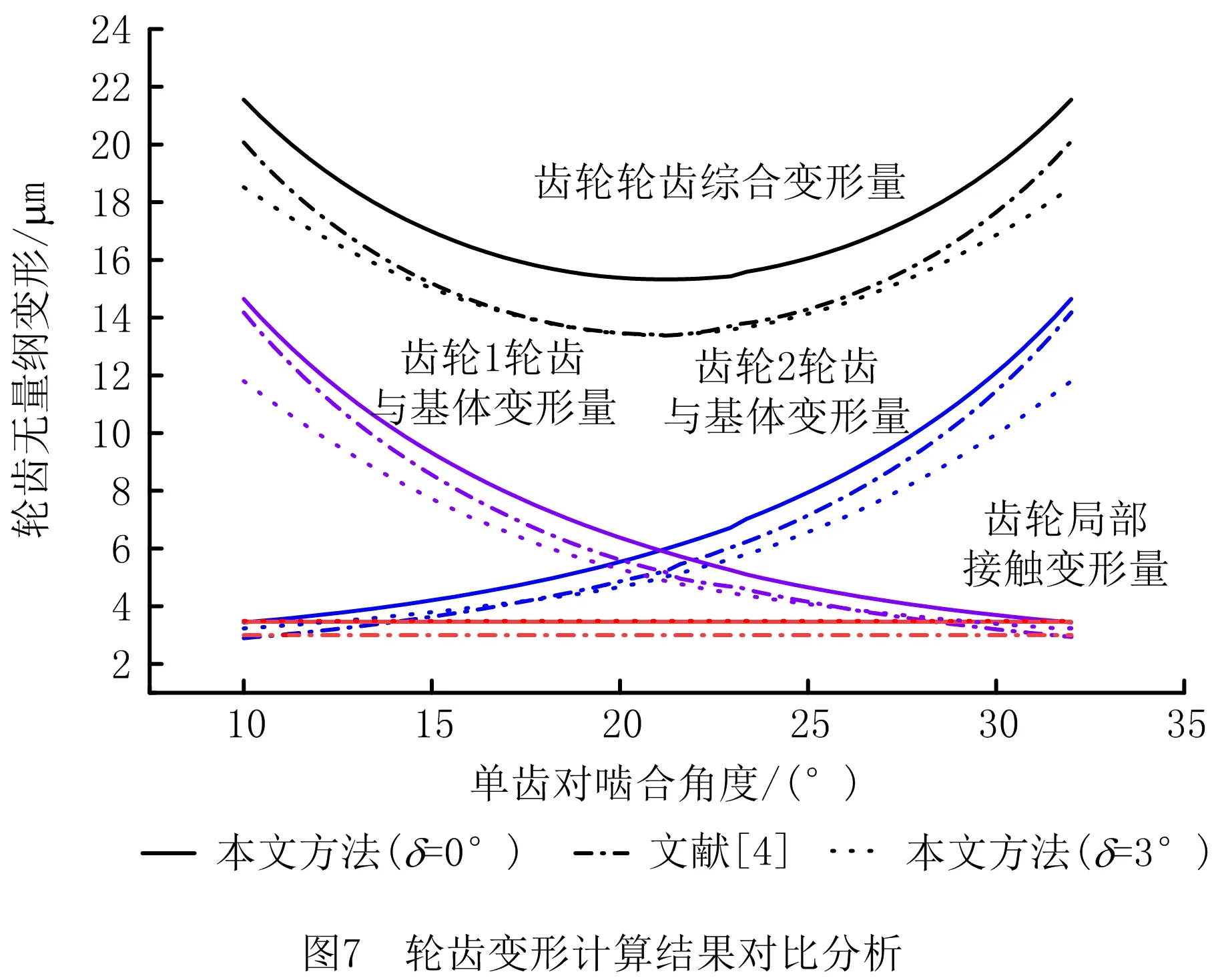
由图7可见，随着变厚齿轮节锥角的增加，轮齿综合变形量逐渐变小，这是由于节锥角会使变厚齿轮在传动过程中产生一定轴向力，导致齿面法向啮合力变小，轮齿综合变形量减少。将图7计算的轮齿变形结果代入式(27)，可得δ=3°的变厚齿轮单齿对啮合刚度的最大值为15.09 N/(mm·μm)。图8所示为传统Weber法和本文改进后Weber法的啮合刚度计算结果对比，因为改进后的Weber法增加了齿轮基圆与齿根圆之间的部分变形，所以实验计算精度提高了4.3%。

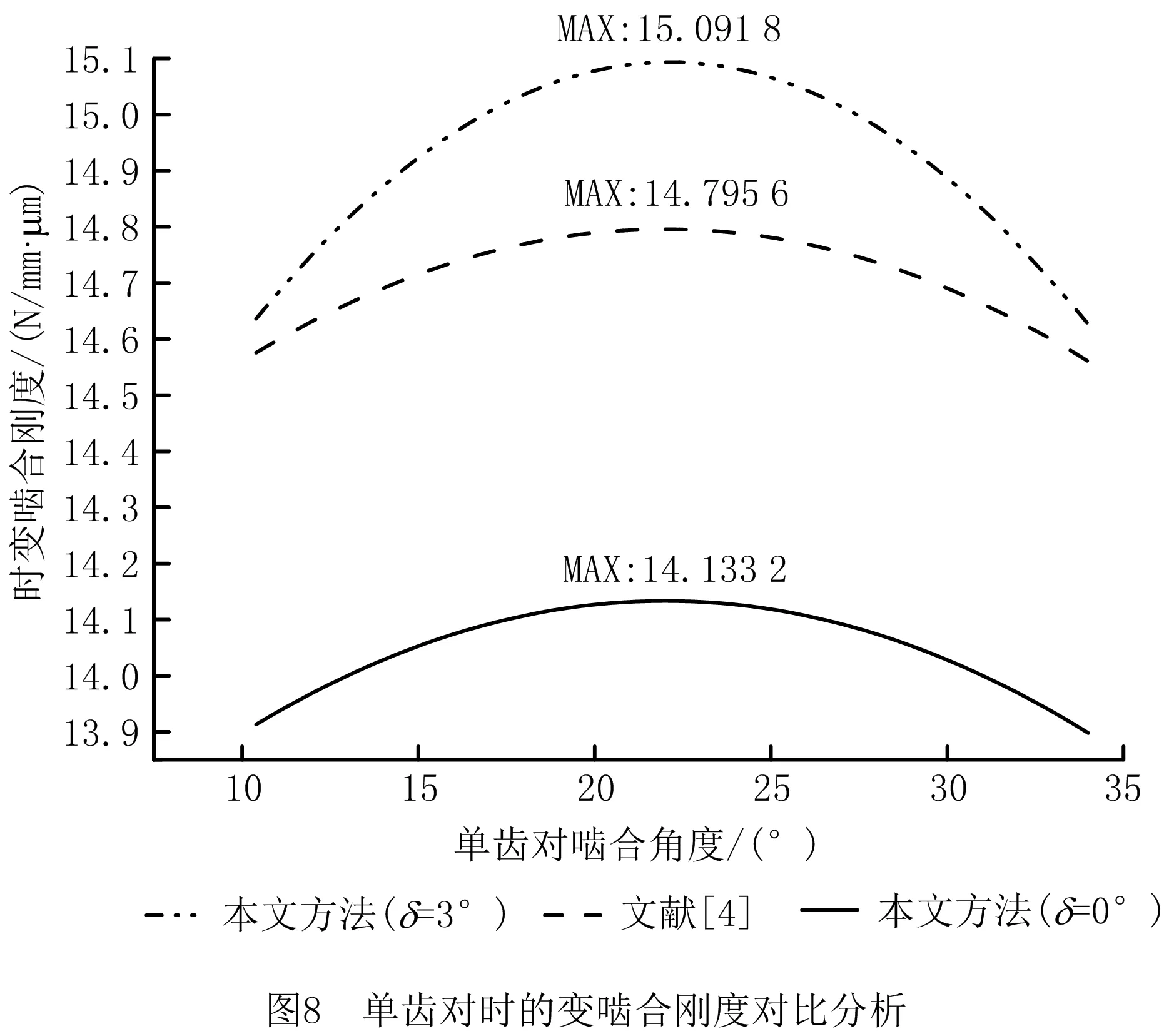
2.3 变厚齿轮时变啮合刚度的比较与验证

为了验证本文变厚齿轮时变啮合刚度求解模型的准确性，本节通过ANSYS有限元分析软件的瞬态动力学分析模块，对表1所示参数的变厚齿轮副进行有限元加载接触分析，其有限元分析模型如图9所示。由于变厚齿轮传动接触具有高度非线性，本文采用柔性体—柔性体的接触类型，设置主动轮转速为50 rpm,从动轮阻力矩为70 Nm，主、从动齿轮材料均为40Cr，弹性模量为206 Gpa，泊松比为0.26。

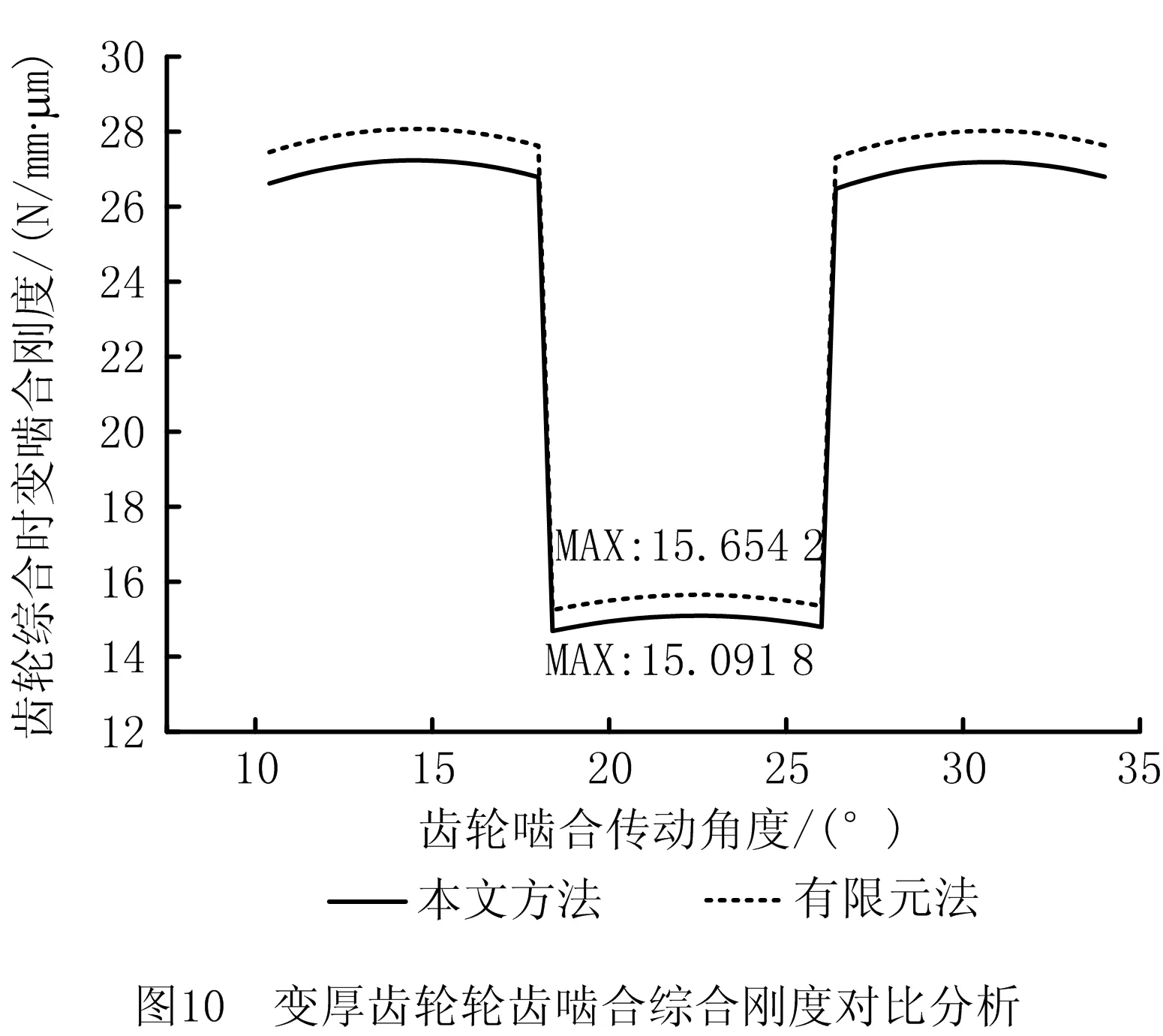
本节通过将变厚齿轮啮合过程离散化，取固定时间步长0.001 s，将啮合过程0.1 s平均分为100时间节点。提取不同瞬时主、从动变厚齿轮的相对转角，采用式(28)将齿轮转角转变为啮合线方向位移，从而获得变厚齿轮时变综合啮合刚度变化曲线(如图10)，其单齿啮合刚度最大值为15.65 N/mm·μm，相比本文方法的计算结果，相对误差为3.7%。

(28)

式中：rb1，rb2分别为主、从动齿轮的基圆半径；θ1(t)，θ2(t)分别为主、从动齿轮的瞬时相对转角。

2.4 变厚齿轮基本参数对啮合刚度的影响

时变啮合刚度是齿轮系统动力学研究的重要参数之一，分析时变啮合刚度的影响因素及其变化规律，对改善变厚齿轮的啮合特性，提高变厚齿轮的传动平稳性具有十分重要的意义。在变厚齿轮的基本参数中，法向压力角、节锥角、齿顶高系数、齿宽等因素均能较好地反映其啮合性能；另外，实际工作中的变厚齿轮通常采用齿向修形的方式改善啮合性能来提高其承载能力[17]。因此，本文采用集中参数法，分别研究上述参数对变厚齿轮啮合刚度的影响规律，为将来的变厚齿轮结构优化设计以及系统动力学研究奠定基础。

(1)法向压力角对变厚齿轮啮合刚度的影响

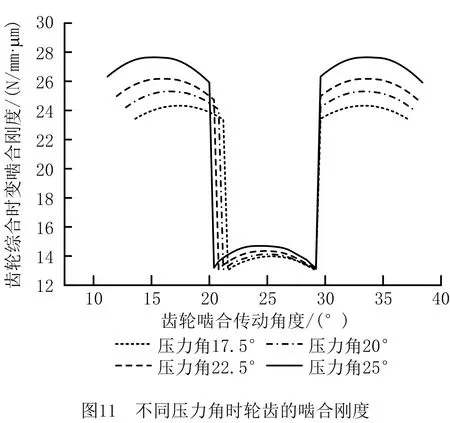
齿轮参数如表1所示，保持其他参数不变，将齿轮副法向压力角的变化范围设置为17.5°～25°。不同法向压力角时轮齿的综合啮合刚度如图11所示，可见当压力角增大时，齿轮齿根处齿厚增大，齿顶处齿厚减小，轮齿齿面曲率半径增大，从而提高了轮齿的综合啮合刚度。然而，随着齿轮法向压力角的增大，齿轮啮合重合度降低，最大差值达到0.19，影响了齿轮传动的平稳性。

(2)齿宽对变厚齿轮啮合刚度的影响

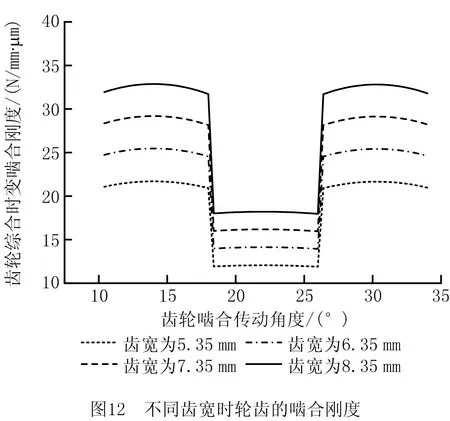
图12所示为齿宽分别为5.35 mm，6.35 mm，7.35 mm，8.35 mm时的变厚齿轮综合啮合刚度曲线，可见变厚齿轮轮齿综合啮合刚度随齿宽的增加而增大，这是由于增加齿宽会减少恒定扭矩下的单位荷载，降低齿轮轮齿的挠曲，从而使变厚齿轮单齿啮合刚度增大，轮齿综合啮合刚度波动值和均值均增大，增大齿宽虽然不影响齿轮的横向接触比，但会增大轴向接触比，使总接触比增大，啮合更加光滑。

(3)节锥角对变厚齿轮啮合刚度的影响

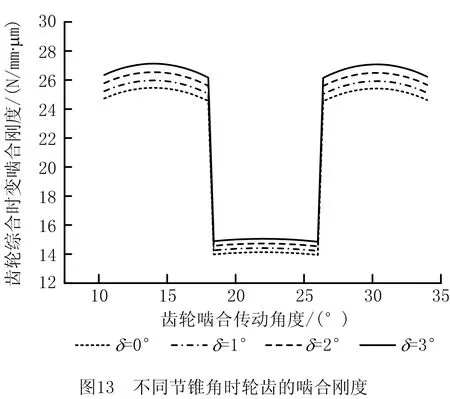
节锥角即变厚齿轮轴线与节锥母线之间的夹角，本文选取节锥角的范围为0～3°，节锥角取不同值时轮齿的综合啮合刚度如图13所示。可见变厚齿轮节锥角对其啮合刚度的影响较小，时变啮合刚度数值随节锥角的增加而增大，节锥角每增加1°，变厚齿轮时变啮合刚度的均值增大2.2%。这是由于增加变厚齿轮节锥角会增大啮合主方向角，从而增大接触比和啮合面积，导致变厚齿轮的单齿啮合刚度增大，啮合刚度均值也增大。

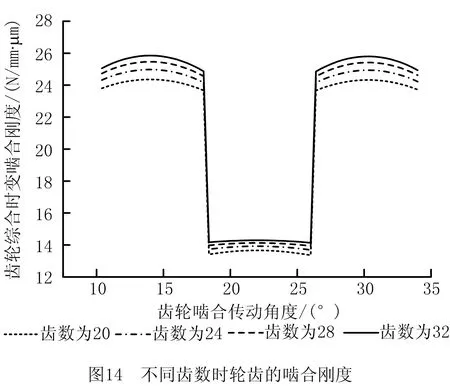
(4)齿数对变厚齿轮啮合刚度的影响

图14所示为主、从动齿轮齿数分别为20，24，28，32时变厚齿轮的综合啮合刚度曲线，可见随着齿轮齿数的增加，齿轮啮合频率增加，其综合时变啮合刚度随之增大。

(5)齿顶高系数对变厚齿轮啮合刚度的影响

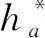
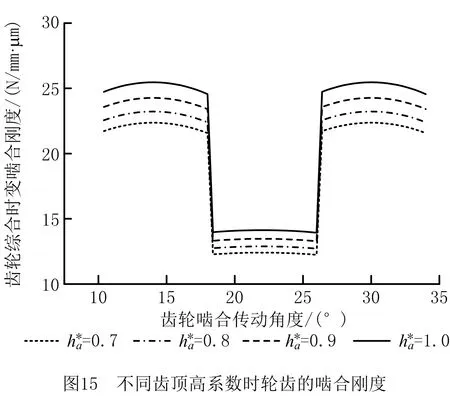
(6)修形量对变厚齿轮啮合刚度的影响

采用表1的齿轮参数，分别计算未修形和齿向修形量为0.5 μm，1 μm，1.5 μm的时变啮合刚度。4种不同齿向修形量时的轮齿啮合刚度对比分析如图16所示，可见随着齿向修形量的增加，轮齿的时变啮合综合刚度随之降低，变厚齿轮传动单齿/双齿交替啮合区的啮合刚度波动逐渐减小。

3 结束语

本文通过对渐开线变厚齿轮沿齿宽方向进行离散化处理，基于切片法建立了一种考虑齿向修形的变厚齿轮时变啮合刚度求解方法，并对传统Weber能量法进行改进，分析讨论了齿轮基圆与齿根圆大小关系对轮齿啮合刚度的影响，增加了齿轮基圆与齿根圆之间的部分变形，提高了齿轮时变啮合刚度的计算精度。在此基础上，研究了变厚齿轮的几何参数和齿向修形量对啮合刚度的影响，得出以下结论：

(1)变厚齿轮的法向压力角、齿宽、修行量对其时变啮合刚度均有明显影响。变厚齿轮时变啮合刚度随法向压力角的增加而增大，但随法向压力角的增加齿轮副重合率降低，将影响变厚齿轮传动的平稳性；增加齿宽会减少恒定扭矩下的单位荷载，降低齿轮轮齿的挠曲，从而使变厚齿轮单齿啮合刚度，以及轮齿综合啮合刚度波动值和均值增大；随着齿向修形量的增加，轮齿的时变啮合综合刚度降低，变厚齿轮传动单齿/双齿交替啮合区啮合刚度波动逐渐减小。

(2)变厚齿轮的节锥角、齿顶高系数、齿数对其时变啮合刚度影响较小。时变啮合刚度数值随节锥角的增加而增大，节锥角每增加1°，变厚齿轮时变啮合刚度的均值增大2.2%。这是由于增大变厚齿轮节锥角会增加啮合主方向角，使接触比和啮合面积增大，导致变厚齿轮的单齿啮合刚度和啮合刚度均值增大；随着齿顶高系数的增加，齿高和接触比增大，使得单齿啮合刚度和综合啮合刚度在一个啮合周期内增大。