考虑客流分布的动车组部件预防性维护决策
王 红,杨国军,何 勇,熊 律
(兰州交通大学 机电工程学院,甘肃 兰州 730070)
0 引言
受节假日等因素影响,我国高速铁路客流在全年不同时段呈现较大波动,例如春运、暑运等客流高峰期常一票难求,客流淡季动车组上座率却明显不足[1-2]。客流量时间序列分布的差异性导致动车组运行工况不同,而且客流分布不均导致动车组运营收益不同,进而使不同时刻的停机维护成本呈现较大差异,如何在不同运行工况下保证动车组可靠运行的同时有效提升维护策略经济性,已经成为铁路运营部门全面推进降本增效的首要问题。
建立时变工况与设备衰退规律的集成模型是研究不同工况下设备维护策略的前提。XIA等[3]基于环境调整因子建立了不同环境工况下的部件失效率演化模型,YOU等[4]通过比例失效模型研究了不同工况水平下的失效率变化规律,然而二者忽略了历史工况对设备失效率函数的影响,不同于比例失效模型,加速失效模型则将不同工况下的服役时间进行等效转化,可以量化历史工况对设备衰退过程的影响[5]。同时,时域范围内的客流分布不均会影响动车组上线需求,从而影响动车组维修计划的制定。以往研究多从运用角度出发对动车组运维计划进行优化[6-8],付建军等[9]为适应客流需求,在优化运维计划时考虑动车组重联和解编;LIN等[10]在优化动车组高级修计划时,通过设定不同时域范围内的维修率来满足不同客流需求下的运用计划。文献[6-10]从客流分布角度出发,对动车组运用计划进行了优化,但未能考虑客流分布对动车组部件维修经济性的影响。
由于动车组不同时段的盈利能力不同(上座率不同),目前动态客流量影响下的动车组运行计划编制方法的研究成果相当丰富[11-13],但针对维护策略的研究鲜有报道。同时,已有的其他生产和维护优化策略也较少考虑局部客流高峰引起的运维冲突,不能适应动车组因客流变化而对维护计划进行的调整。因此从维护经济性的角度出发,对客流分布不均下的维护策略调整方法进行研究十分必要。
本文基于加速失效模型建立了客流分布不均下的动车组部件可靠度演化模型,以维护成本为优化目标,建立了不同客流分布下的动车组部件维护调整策略,并将所提维护模型与不考虑客流分布不均的维护模型进行对比分析,以验证其合理性和有效性。
1 问题描述与假设
动车组客流在时域范围内分布不均使动车组客流工况存在差异,影响动车组部件可靠度衰退速率;同时由于动车组上线率要求随客流需求动态变化,当在客流高峰期对动车组进行维护时将产生较大的经济损失。为减少运维冲突,需对动车组维护计划进行局部修正。因为提前送修会增大维护成本,延迟维护又会有较大的失效风险,所以以客流工况下的部件可靠度模型为基础,在客流高峰期权衡可靠性和经济性要求对维护计划进行修正是必要的。结合动车组现场检修制度及本文研究内容,做出如下假设:
(1)部件从全新状态开始投入运营,初始役龄为0。
(2)部件在不同客流量作用下的失效机理不发生改变,服从加速失效模型。
(3)动车组部件备件不足的情况较少,因此不考虑由备件不足引起的维修等待,各种故障能被及时修复。
(4)部件基准故障率服从形状参数为m、尺度参数为η的两参数威布尔分布。
(5)假设短期内客流突变不影响部件可靠度和故障率衰退过程,客流区间内的平均客流量λi可以表征其客流水平。
2 维护模型的建立
2.1 客流分布下的故障率模型
文献[2]统计了京沪高铁全年的客流分布,其时间序列呈现离散分布。因此借鉴可靠性分析中对离散环境应力的等效处理方法[14-15],将客流数据作分段等效处理,以获得不同客流区间内的等效平均客流量。定义不同客流区间的客流因子εi来反映其客流量变化规律,
εi=λi/λ0。
(1)
式中:λi为第i个客流区间的等效平均客流量;λ0为部件基准运量。
可靠性分析通常采用加速失效模型对不同工况下的等效役龄进行转换[5],不同客流量作用下的部件等效服役寿命不同,将其换算到基准运量下的等效役龄
l0i=liεi。
(2)
式中li为客流区间长度。
不同客流量作用下动车组部件的有效役龄不同,可通过加速失效模型进行转换[5]。如图1所示,部件经历n个客流区间后的等效役龄为
(3)

当部件经历n个客流区间后,根据可靠性理论中可靠度函数与故障率函数间的关系,部件的可靠度
(4)

根据可靠性知识,部件故障率函数与可靠度函数存在如下数学关系:
h(l,n)=(dR(l,n)/dl)/R(l,n)。
(5)
结合式(4)和式(5),执行预防性维护活动前第n个客流区间内部件的故障率函数为
(6)
维护活动虽然能改善设备当前的运行状态,但是修复后设备的衰退速率较维修前加快。为刻画维护活动对部件衰退过程的影响,基于失效率调整因子的修复非新模型[16-17]被广泛引用,根据其演化规则,第k次维护后设备的故障率函数
(7)
式中:ak为役龄回退因子;bk为故障率递增因子;Lk为第k个预防性维护周期。
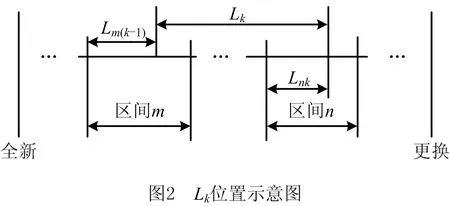
如图2所示,假设维护周期Lk位于客流区间m和n之间,考虑动态客流变化对故障率函数的影响时,Lk内的故障率函数
(8)
式中L0k为维护周期Lk转换为基准客流工况下的等效维护周期,根据式(8)可知维护周期Lk的内部件故障率函数,由可靠度函数与故障率函数的数学关系知此时部件的可靠度函数可相应确定。
2.2 维护调整策略
由于我国高铁客流量在全年范围内分布不均,动车组在不同时段内进行停机维护造成的盈利损失不同。多数文献计算停机成本时仅考虑了停机时间,对于动车组列车来说,其停机成本应随客流需求动态变化,则动车组部件第k次预防性维护的单次停机损失成本
Csk=tk×λi×r。
(9)
式中:tk为维护停机时间,包括故障维修用时和预防性维护用时;λi为第i个客流区间内的等效平均客流量;r为单位客流量收益。总停机损失成本CS为每次停机损失成本Csk的总和。根据假设(3),维护活动及时开展,因此每次维护的停机时间相同。
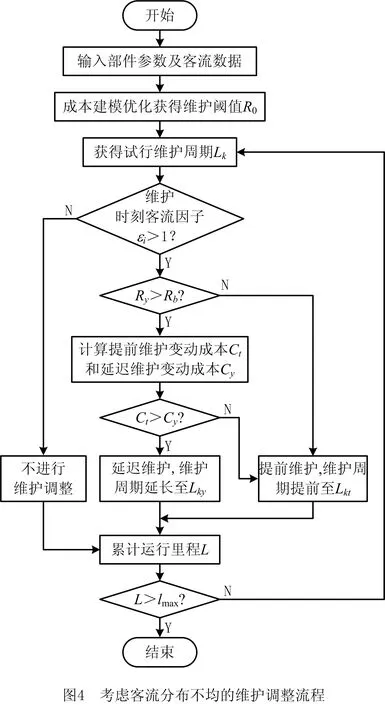
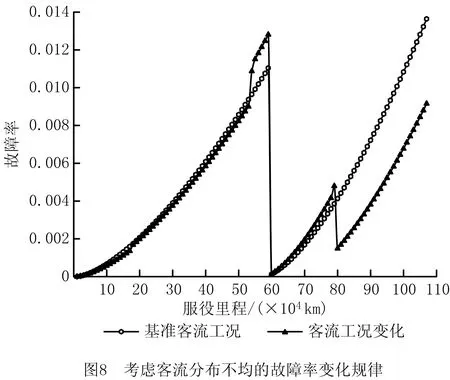
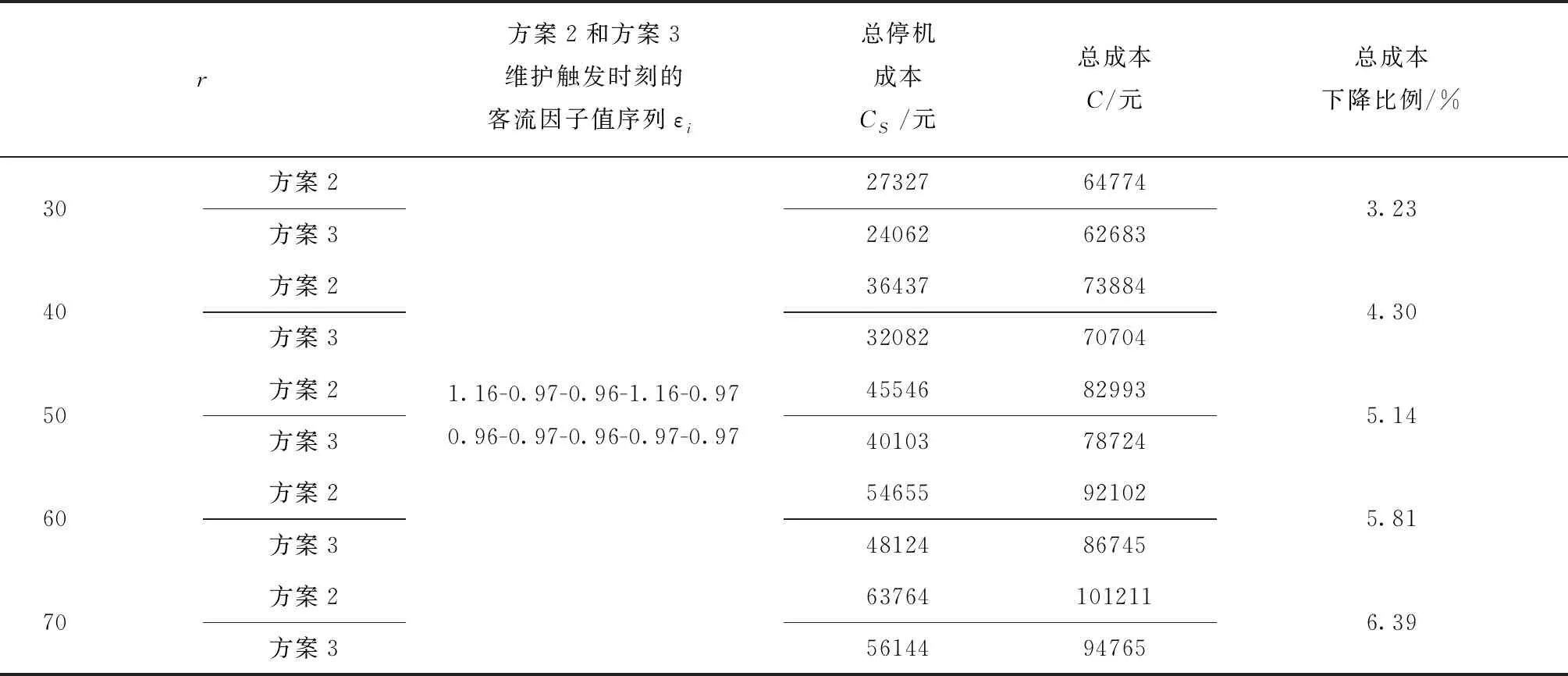
图3所示为维护时刻调整示意图,其中PM1,PM2,PM3分别为不考虑维护调整时第1,2,3次预防性维护时刻,PM2t为维护提前时第2次预防性维护时刻,同理PM2y为延迟维护时第2次预防性维护时刻。为避免较大的停机损失,客流高峰期时需要对动车组部件进行提前/延迟维护。提前对动车组部件进行维护将浪费其使用价值,而延迟进行维护则承担一定失效风险,为保障安全,延迟维护必须在可靠度限制范围内进行。文献[18]将不可容忍阈值Rb作为延迟维护的可靠度约束,当Rb≤R≤R0时,设备允许延迟维护。根据文献[18],为保证行车安全,R CY=cy(R0-Ry)/(R0-Rb)。 (10) 式中:cy为延迟维修的基本惩罚成本;Ry为延迟维护后动车组部件的可靠度值;R0为部件预防性维护阈值。 维护提前可以充分保证设备在客流区间n内的服役可靠性,但会浪费设备的使用价值,造成经济损失,浪费成本CL的计算公式为 CL=cr(Rt-R0)/(1-R0)。 (11) 式中:cr为每次维护的可靠度利用价值;Rt为预防性维护提前后部件的可靠度。 动态维护调整会使部件在不同周期内的失效概率发生变动,由此引起的故障维修变动成本为 (12) 式中:cd为单次故障维修成本;Δl为动态调整时动车组部件维护周期调整量。 结合式(11)和式(12),部件提前维护变动成本Ct与延迟维护变动成本Cy分别为: Ct=CL-ΔCd; (13) Cy=CY+ΔCd。 (14) 假设动车组部件在生命周期lmax内因客流需求影响而进行了j次维护调整,则其由动态维护调整引起的变动成本为 (15) 式中γ的取值由两种调整成本的大小来决策,提前维护时γ=1,延迟维护时γ=0。 由上文所述,客流分布不均下部件的维护调整策略流程如图4所示。 假设动车组部件在更换周期内进行了k次预防性维护,则动车组部件运行过程中的总成本C包括总停机损失成本CS、维护调整引起的变动成本ΔC、预防性维护成本Cp和故障维修成本Cd。由2.1节和2.2节建模得到优化模型如下: min(C)=CS+ΔC+Cp+Cd。 (16) s.t. 0≤L≤lmax; Rb≤R。 通过求解约束条件下设备总成本的最优值min(C),可以获得动车组部件在更换周期内的最优维护计划。 为验证上述模型的有效性,以动车组四级修时更换的某部件为例进行实例分析。根据假设(4),动车组部件在基准客流工况下的故障率函数为 (17) 以文献[2]中京沪高铁客流量数据为基础,借鉴可靠性分析中对离散环境应力等效时的多项式拟合和动态应力等效方法[15-16]对客流数据进行近似等效,结果如图5和图6所示。 由图5可见,全年的客流数据存在4个变化趋势比较明显的波峰,为体现客流量的分阶段变化,将全年划分为波动比较明显的4个客流区间。文献[2]中的数据以自然年为统计范围,而生产实际中动车组维护周期主要以走行公里数为依据,因此将其时间序列与日走行公里数相乘得到具体的客流分布区间和因子值(京沪高铁对发里程为2 636 km,近似处理取日走行公里数3 000 km)。等效后的客流变化如表1所示。 表1 客流区间及客流因子值 不同客流分布下的设备可靠度和故障率函数变化规律与恒定客流相比有一定差异。设恒定客流下的客流因子为1,则考虑客流分布下的可靠度和故障率函数变化如图7和图8所示。 结合表1、图7和图8可知,维护周期1内的客流因子(0.85~0.96)较小,而周期2内的客流因子(1.16~0.97)略大,同时可得客流分布不均时动车组部件的可靠度和故障率与恒定客流时相比差别较大。因此,建立可靠度和故障率模型时充分考虑客流分布不均造成的影响,有利于科学评估其衰退过程。 对动车组维护周期进行决策通常以可靠度为约束条件,为探究动车组部件的最优可靠度阈值,本文对可靠度—维护成本进行数值仿真分析,设定可靠度优化范围为0~0.97,步长为0.01,优化结果如图9所示。 由图9可见,可靠度阈值过低时维护总成本较高,表明可靠度阈值较低时的维护次数虽然较少,但是失效风险较大,因此障维修成本较高;可靠度阈值过高时,设备需频繁维护以保证可靠度要求,预防性维护成本急剧增大,因此维护总成本也较高。图9中3条C-R曲线r的取值依次为50,40,30,由优化结果可知,r值越大,优化得到的可靠度阈值越低,表明设备需要维护的次数越少,即随着客流需求的增大,设备应减少维护次数,避免停机维护对设备运用的干扰,这与生产实际相符。为了避免可靠度阈值过低引起的维修不足与可靠度阈值过高时引起的维修过度,本文取3种r取值下的最优可靠度阈值之一R0=0.8为例进行计算,此时r=40。 表2所示为3种不同维护方案的对比。其中,方案1维护模型未考虑客流分布对动车组部件可靠度的影响,方案2维护模型仅考虑了客流分布不均对部件可靠度的影响,而方案3维护模型综合考虑了客流分布不均对部件可靠度和维护策略经济性的双重影响。通过比较分析3种维护方案,得出以下结论: (1)对比方案1和方案2,考虑客流分布时动车组部件更换周期内的成本会小幅下降,这是因为考虑客流分布时的可靠度和失效率评估更加准确,欠维护的情况较少,更能保障动车组部件的可靠性,使其故障成本下降进而降低维护总成本。可见方案2对可靠性的评估更加准确,能够避免故障维修成本上升。 (2)对比方案2和方案3,方案3较方案2的设备维护总停机成本下降了11.9%,虽然由部分区间维护延迟/提前引起成本变动,导致维护成本上升,但是总成本呈下降趋势,下降值为4%。即使有部分周期(周期2和周期4)为了避免在停机成本较大的区间内维护而延迟维护,降低了一定的可靠度,但是均在Rb限制范围内。 表2 不同方案下的维护计划结果对比 综上所述,与不考虑客流分布的维修方案相比,方案3不仅能够准确评估动车组部件的可靠度,还能通过维护调整不同客流分布下的动车组部件,从而有效降低维修成本,提升维修经济性。 不可容忍阈值Rb是影响设备维护调整策略的重要指标,其量化了设备的可靠度调整范围。为探究不同不可容忍阈值下的成本变动情况,在方案3中取Rb=0.75。进一步对方案3进行分析,保持维护阈值R0=0.8,分别取Rb=0.70,0.73,0.75,0.77,0.79,不同Rb下的维护变动成本如表3所示。 表3 不同Rb下的维护变动成本 由表3可知,当Rb过低或过高时,变动成本均较大;Rb过低时,设备维护调整范围增大,相应的故障风险上升,导致故障维修成本攀升;Rb=0.77,0.79时,过于接近预防性维护阈值,所有维护活动均提前,产生的设备使用价值浪费较大。因此,为保证一定的调整范围并减少故障成本,文中取Rb=0.75。 考虑客流需求影响,在客流高峰期对动车组部件维护计划进行调整可以有效避免运维活动冲突,降低维护总成本。上文分析中,部件在不同客流收益下的停机成本是进行维护调整的重要依据,而单位客流量收益r是量化部件停机成本的重要指标。为探讨不同停机成本对本文调整策略经济性的影响,保持其余参数不变,对方案2和方案3在不同单位客流收益r下的维护成本进行分析比较,结果如表4所示。 由表4可知,单位客流收益r变大时,方案2和方案3维护触发时刻的客流因子值序列不变,但方案3较方案2的总停机成本和总成本均呈现下降趋势,同时方案3较方案2的总成本下降比例也随r的增大而增大,表明部件停机成本较大时,对部件进行维护调整更能节省维护总成本,本文模型的经济性优化效果更好,因此本文所提策略在实际生产中更适用于停机成本较大的动车组部件。 表4 单位客流收益r不同取值下方案2和方案3的维护成本比较 考虑到客流分布不均对部件可靠度和维护经济性的影响,本文提出客流分布不均下的动车组部件动态维护调整策略,并与不考虑客流分布的维护方案进行了比较。研究结果表明,可靠度模型中考虑客流分布不均时对部件可靠度的评估更加准确;充分考虑客流需求对维护活动进行动态调整,避免在客流高峰期停机维护,能够有效降低动车组的停机成本,降低维修总成本。 作为维护动态调整策略的关键参数,部件的不可容忍阈值通过敏感性分析可以确定部件客流分布不均下的最佳调整方案。合理设定部件不可容忍阈值与维护阈值,能够使部件的停机维护时刻有效避开客流高峰期,从而提升动车组维修的经济性。 本文以客流分布为基础进行动车组部件动态维护决策,可为制定单设备维护计划提供参考。然而,不同部件的维修参数不同,对各设备进行维护时会导致频繁停机,考虑客流分布不均时的维修决策问题将会比较复杂,因此后续研究将进一步探究客流分布不均下的多设备维护决策问题。

2.3 目标函数
3 算例分析及比较




3.1 维护策略比较分析



3.2 参数敏感性分析
4 结束语

