考虑磨损与变形的谐波齿轮精度可靠性分析与优化设计

潘柏松,方 宽,文 娟,项涌涌，翁微妮

(1.浙江工业大学 机械工程学院，浙江 杭州 310014； 2.浙江工业大学 特种装备制造与先进加工技术教育部重点实验室，浙江 杭州 310014；3.博世电动工具(中国)有限公司，浙江 杭州 310052)

0 引言

谐波齿轮减速器广泛应用在航空航天、工业机器人、雷达系统、通信设备等诸多领域，相比其他齿轮减速器具有体积小、传动比高、载荷大等优点[1]，多用于低转速、高精度的情况，如人造卫星太阳能板展开、雷达系统转动、机械臂精准移动等[2]。工程实际中，谐波齿轮不可避免地存在制造加工、部件装配等产生的静态误差以及柔轮摩擦磨损[3]和变形[4]导致的动态误差。由于磨损和变形均为高度非线性动态因素，若不考虑影响因素进行谐波齿轮传动分析和设计，将极大影响齿轮的传动精度，从而直接影响装备整体寿命和可靠性。因此，综合考虑静态和动态影响因素对谐波齿轮进行传动精度可靠性分析和优化设计不但十分必要，而且具有重要的工程意义。

近年来，针对谐波齿轮传动误差问题，国内外学者开展了一系列研究。TUTTLE等[5]对谐波齿轮的传动误差来源进行数学分析，得出传动误差是由装配误差和3个主要部件的制造误差所造成的结论；国内学者辛洪兵[6]采用随机过程理论推导出较全面考虑误差因素的谐波齿轮传动误差计算公式。上述对传动误差的研究仅考虑了装配和加工制造因素，实际传动中还存在动态影响因素。针对柔轮内壁与柔性轴承外圈的磨损动态因素，郭宣瑾[7]研究了在不同负载和柔轮壁厚下的柔轮摩擦磨损情况，并通过实验分析了不同载荷和转速的磨损机制变化规律；张金洋等[8]研究了在制造、加工因素以及柔性、摩擦等动力学因素综合作用下的谐波齿轮传动精度；李俊阳等[9]对谐波齿轮进行磨损寿命试验，研究了磨损表面接触体的载荷比例与负载、转速等之间的关系；李俊阳[10]还构建了基于Archard模型的柔轮内壁与柔性轴承外圈间混合润滑磨损模型。上述文献对谐波齿轮的动态磨损进行分析与研究，但所构建的磨损模型未考虑减速器传动过程中波发生器对柔轮的冲击，以及柔轮传动过程中柔性变形的情况，难以准确反映谐波齿轮减速器的实际磨损情况。另外，在谐波齿轮正常工作中还伴随着柔轮的周期性柔性变形，柔轮变形是保证齿轮正常传动的必要条件之一[11]，为构建更符合实际的传动误差模型，需要对柔轮变形因素开展研究。GHORBEL等[12]对柔轮变形进行了实验，结果表明柔轮变形是传动误差中高频误差分量的主要影响因素；银国伟[13]对不同的柔轮材料进行径向变形试验，得到柔轮径向变形与所受径向力之间的关系；柴文杰[14]对谐波减速器柔轮变形特性展开研究，分析了柔轮在速度和载荷条件下的径向位移变化规律。上述文献研究了转速和负载对柔轮变形的影响，但未考虑柔轮变形对齿轮传动精度的影响。为此，本文在现有柔轮变形研究的基础上，研究柔轮变形对传动误差的影响，并综合考虑磨损和变形因素对谐波齿轮进行传动误差建模。

在谐波齿轮的可靠性分析方面，国内外学者也进行了比较多的研究。TAGHIRAD等[15]针对谐波齿轮的复杂动态特性，建立了考虑齿轮顺应性、滞后性以及各部件间摩擦的动力学模型，并对不同工况进行可靠性分析；JOHNSON等[16]考虑实际工作中谐波齿轮可靠性较低的问题，提出一种通过增强齿轮部件刚度来提升可靠性的方法，并进行了相关试验验证；LI等[17]针对谐波齿轮制造和工作过程中性能下降的问题，提出一种考虑多源不确定性和磨损的谐波齿轮性能裕度建模及可靠性分析，但该模型未考虑柔轮变形的影响因素；张乙[18]研究了在多失效模式相关下谐波减速器系统的时变可靠性，提出一种基于Copula函数的多失效模式相关下时变可靠性分析方法。在多种因素影响下，谐波齿轮的传动精度可靠性会随工作时间的增加而下降，即产生时变可靠性。张金洋等[8]考虑谐波齿轮动力学因素，并基于多项式混沌展开法(Polynomial Chaos Expansions, PCE)进行可靠性分析，但模型中未具体分析动态影响因素；王磊[3]研究了谐波齿轮的磨损因素，构建了考虑磨损的精度时变可靠性模型。上述国内外对谐波齿轮传动精度可靠性的研究未综合考虑磨损与变形这两个重要的动态影响因素，难以获得真实有效的减速器精度可靠性分析结果，以至于影响优化设计结果的准确性。

综上所述，本文综合考虑谐波齿轮的各类加工装配误差、磨损因素和变形因素，对齿轮开展传动精度可靠性分析及优化设计研究，通过综合分析传动误差的静态和动态影响因素建立了谐波齿轮传动误差模型。针对谐波齿轮中柔轮与柔性轴承间的磨损情况，基于磨损经验模型和磨损试验数据，应用贝叶斯修正方法建立动态磨损模型。在研究柔轮变形方面，根据获得的柔轮变形试验数据和高斯过程(Gaussian Process, GP)回归方法建立柔轮变形预测模型。综合获得的传动误差模型、动态磨损模型和变形模型建立谐波齿轮精度可靠性模型，应用基于拉丁超立方抽样(Latin Hypercube Sampling,LHS)的Kriging代理模型和蒙特卡洛法(Monte Carlo Simulations, MCS)求解谐波齿轮传动精度可靠度。对谐波齿轮误差参数进行灵敏度分析，确定设计变量，以加工成本最低为优化目标、传动精度可靠度和磨损量为约束条件建立公差优化设计模型，并使用序列二次规划法(Sequential Quadratic Programming, SQP)进行优化设计。

1 谐波齿轮减速器传动误差分析

谐波齿轮减速器主要由刚轮、柔轮、波发生器三大部件组成，其结构与原理图如图1所示。根据传动原理及传动方式，谐波齿轮的传动误差可分为刚轮和柔轮的加工误差、刚轮和柔轮的装配误差以及波发生器部件误差[11]。

谐波齿轮中，刚轮和柔轮的制造加工误差由齿轮周节累积误差和切向相邻齿综合误差构成，刚轮制造加工误差为

(1)

式中：ΔFp1为刚轮周节累积误差；ωWG为波发生器旋转角速度；Δff1为刚轮切向相邻齿综合误差；ZCS为刚轮的齿数。

柔轮制造加工误差为[8]

(2)

式中：ΔFp2为柔轮周节累积误差；ZFS为柔轮的齿数；Δff2为柔轮切向相邻齿综合误差。

由于谐波齿轮各个零件本身存在误差，在安装过程中必然会出现实际位置偏离理想位置的现象，产生装配误差[19]，其主要误差为刚轮安装孔、柔轮装配轴承、输出轴装配等各零件装配间的径向跳动、配合间隙和径向游隙，上述各类误差导致刚轮和柔轮出现偏心误差。以刚轮偏心矢量误差ΔEtCS为例，图2所示为ΔEtCS的几何简图，偏心矢量在τ-τ方向上不产生传动误差，在啮合线n-n方向上产生偏心误差ΔECS，同理可知柔轮的偏心误差ΔEFS。

在刚轮与柔轮之间，各项由装配引起的运动误差可以由刚轮固定不动偏心误差源所产生的运动误差ΔzCS和柔轮旋转偏心误差源所产生的运动误差ΔzFS表示，表达式分别为：

(3)

式中：ΔECS为影响刚轮安装精度的配合间隙和跳动的偏心误差值；φCS为相应的偏心误差向量相位角；αn为啮合角；eCS为影响刚轮安装精度的配合间隙和跳动误差，包括刚轮与安装孔间的径向跳动误差eCS11及刚轮和安装孔间的配合间隙误差eCS12。

(4)

式中：ΔEFS为柔轮配合间隙和跳动的偏心误差值；φFS为相应的误差相位角；eFS为柔轮配合间隙和跳动误差，包括柔轮与输出轴之间的配合间隙误差eFS11和输出轴的径向跳动误差eFS12。

波发生器部件的误差主要考虑径向误差和偏心误差，包括随波发生器转动与不随波发生器转动两部分误差。由文献[19]可知，波发生器部件误差中还包括由磨损和变形动态因素引起的传动误差，这两种因素所产生的传动误差对整个谐波齿轮的传动精度也有很大影响。

在传动过程中，柔轮内壁与柔性轴承外壁间存在摩擦磨损。根据文献[20]可知，柔轮与柔性轴承间的动态磨损量可等效为柔性轴承径向游隙与配合间隙的增加量，则波发生器径向动态误差Δxra可表示为动态磨损量所造成的误差与不随波发生器转动的误差之和，即

(5)

式中：ΔxWG1为不随波发生器转动的偏心运动误差；eV(T,v,t)为动态磨损量造成的误差，T为输出端负载，v为输入端转速，t为齿轮工作时间；eWG1为不随波发生器转动的配合间隙和跳动误差，包括柔性轴承径向间隙误差eWG11和柔性轴承径向跳动误差eWG12；φWG1为偏心向量的初始相位角；V(T,v,t)为动态磨损量。

波发生器的椭圆凸轮在谐波齿轮工作时进行转动，柔轮受椭圆凸轮长轴挤压产生径向变形，该变形量会对齿轮的传动精度产生影响[19]。因此，柔轮变形是波发生器转动中必须考虑的因素。波发生器动态偏心误差Δxec可表示为随波发生器转动的偏心误差与柔轮变形造成的误差之和，即

(6)

式中：ΔxWG2为随波发生器转动的偏心运动误差；eB(T,v)为柔轮变形径向位移造成的误差；eWG2为随波发生器转动的配合间隙误差，包括凸轮与柔性轴承的配合间隙误差eWG21和柔性轴承与柔轮的配合间隙误差eWG22；φWG2为偏心误差向量与初始设定轴的夹角；B(T,v)为柔轮变形的最大径向位移量。

由文献[11]可知，谐波齿轮传动误差的统计计算式为

(7)

式中ej为各项跳动和配合间隙。

将谐波齿轮传动误差Δxm转化为传动误差角Δθout[21]，

(8)

式中：kb为相关系数；N为同时啮合的轮齿对数；d1为从动齿轮节圆直径(单位：mm)。

通过综合分析谐波齿轮传动误差，结合式(5)～式(7)，得到考虑磨损与变形的谐波齿轮传动精度模型

(9)

式中ei为除波发生器径向动态误差和动态偏心误差以外的其他各项配合间隙和径向跳动误差。

2 磨损与变形模型的建立

在实际传动过程中，谐波齿轮受摩擦磨损和结构柔性变形影响，第1章建立了考虑磨损与变形的谐波齿轮传动精度模型，本节针对这两个影响因素展开研究。

2.1 柔轮磨损模型

磨损是影响传动精度最典型的因素之一，其随齿轮工作时间的增加而呈非线性变化。在谐波齿轮传动过程中，最主要的磨损位于柔轮内壁与柔性轴承外圈处[3]，因此本文主要分析柔轮与柔性轴承之间的摩擦磨损。由于谐波齿轮柔性轴承外圈材料GCr15的硬度高于柔轮材料40Cr的硬度，该处的摩擦磨损主要发生在柔轮内壁处，如图3所示。

2.1.1 柔轮动态磨损分析

谐波齿轮柔性轴承与柔轮之间采用脂润滑方式，其表现形式为混合润滑，主要失效形式为黏着与磨粒磨损。由文献[10，22]可知，谐波齿轮内壁在混合状态下的黏着磨损模型表示为

(10)

该磨损经验模型未考虑谐波齿轮传动过程中的冲击影响及柔轮的柔性变形，与实际的谐波齿轮传动磨损情况有一定偏差。为使模型更准确地表征齿轮实际工作中的磨损情况，本文采用贝叶斯模型修正方法[23]对原磨损模型进行修正。根据文献[23]可知，贝叶斯修正方法的表达式为

rre(s)=r(s)+Δδ(s)+ε。

(11)

式中：s为模型输入变量；rre(s)为修正后的模型；r(s)为原模型；Δδ(s)为误差项；ε为误差随机变量，ε～N(μ，σ2)。

在谐波齿轮传动过程中，柔轮内壁处的磨损量是一个与负载、转速、时间因素有关的时变动态磨损累积过程，本文将磨损量表示为V(T,v,t)，则贝叶斯修正方法中的输入变量为s=(T,v,t)，修正后柔轮内壁处的磨损模型表示为

Vre(T,v,t)=V(T,v,t)+ΔV(T,v,t)+ε。

(12)

2.1.2 柔轮磨损试验

为研究谐波齿轮柔轮在实际传动过程中的磨损情况，与国内某谐波减速机制造企业合作研究，根据谐波齿轮实际工况下的输出端负载和输入端转速，对该企业某型号谐波齿轮进行柔轮磨损试验。图4所示为不同工况下的柔轮内壁磨损图，图中可以明显看出不同工况下的柔轮磨损。

如图5与图6所示，为了准确测量柔轮内壁处的磨损量，采用线切割的方法从柔轮中切得磨损样品，再采用基恩士超景深显微镜测量样品的磨损量，本文取未磨损表面到磨损最深处的最大磨损量。谐波齿轮柔轮内壁磨损试验的各种工况参数如表1所示。

为研究磨损经验模型与实际传动磨损的偏差，对表1中不同工况的各谐波齿轮，采用磨损经验模型计算相应的磨损值，将其与实际磨损值相减的绝对值作为磨损偏差值。图7所示为各编号谐波齿轮柔轮的磨损偏差量，可见磨损经验模型的磨损计算值与柔轮试验磨损值存在较大偏差。

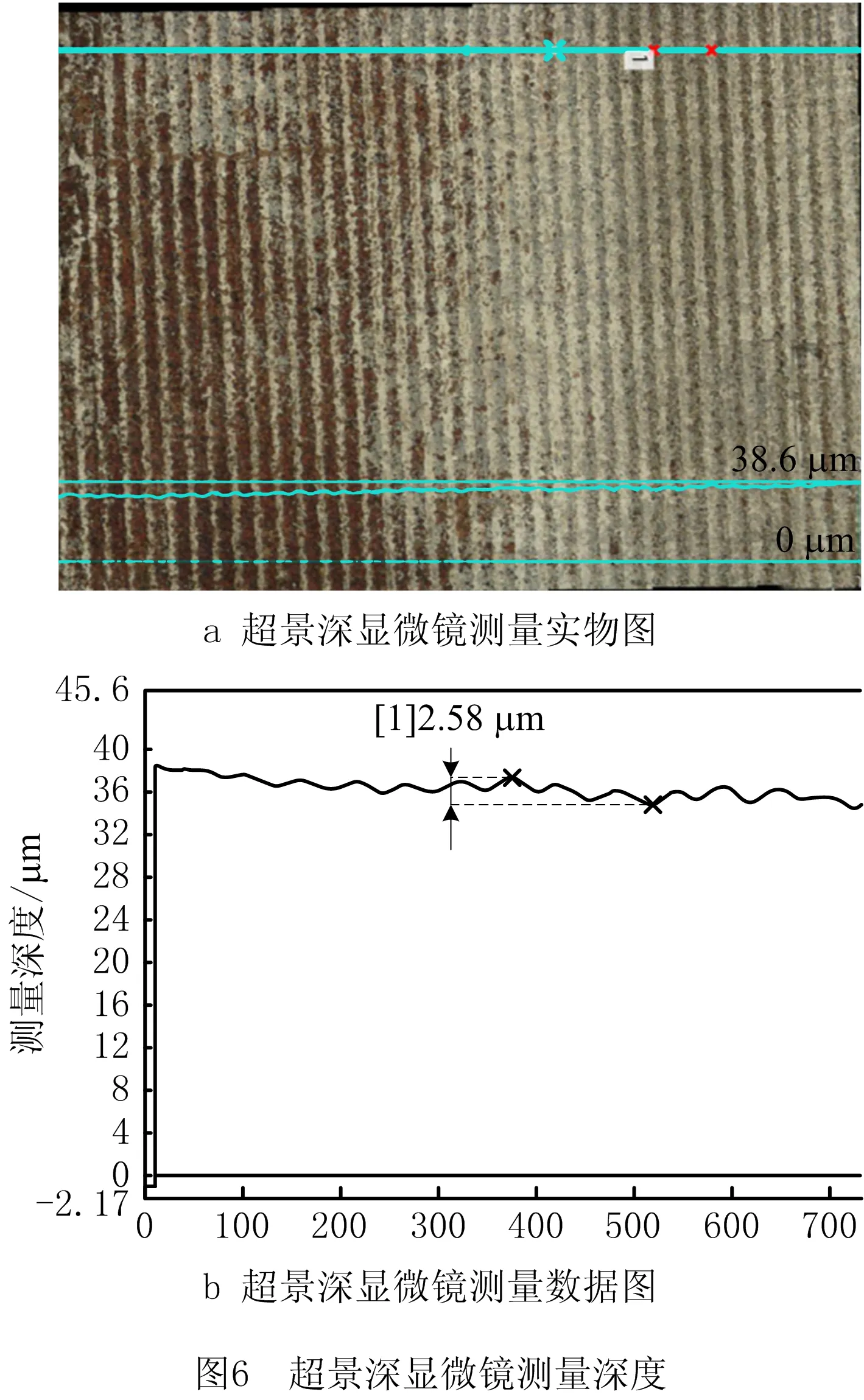
表1 不同工况下的谐波齿轮柔轮磨损量

2.1.3 修正后的柔轮磨损模型

磨损经验模型与实际柔轮磨损的偏差值随负载、转速和时间的变化是一个非线性随机过程，难以用公式表征。高斯过程回归是一种基于贝叶斯理论与统计学习理论发展而来的机器学习方法，对处理小样本、非线性问题具有很好适应性[24]，因此本文用该模型对柔轮磨损偏差量ΔV进行表征。对于噪声α～N(0，σ2)的GP模型可表示为

f(x)～GP(m(x),k(x,x′)+σ2E)。

(13)

式中：m(x)为均值函数；k(x,x′)为协方差函数；x和x′分别为训练样本和预测样本的输入值；E为b维单位矩阵，b表示样本数量。

通过贝叶斯估计得到训练样本输入值x和预测样本输入值x′的联合高斯分布

(14)

式中：y为训练样本输出值；y′为预测样本输出值；k(x,x)为训练样本的方差；k(x,x′)为训练样本与预测样本的协方差矩阵；k(x′,x)为预测样本与训练样本的协方差矩阵；k(x′,x′)为预测样本的方差。

在谐波齿轮工作过程中，工况参数为负载T、输入端转速v和工作时间t，将工况参数和对应的磨损偏差量ΔV作为训练样本，则谐波齿轮磨损偏差项预测模型可表示为

(15)

为验证采用GP建立的磨损偏差项预测模型的准确性，在工况参数(负载T=17.5 N·m，输入端转速v=100 r / min)下对预测模型进行验证，表2所示为该工况下不同时间的谐波齿轮柔轮内壁磨损量。

表2 某工况下的柔轮内壁磨损量

为了保证模型验证的准确性，本文设定95%置信区间来检验预测值和实测值的偏差度[25]。由图8可知，实测磨损偏差值均位于磨损偏差预测均值的95%置信区间内，该模型可用于预测谐波齿轮的磨损偏差项。

对于得到的磨损偏差项预测模型，将其与磨损经验模型相加得到谐波齿轮修正后的磨损模型

Vre(T′,v′,t′)=Vor(T′,v′,t′)+ΔV*(T′,v′,t′)

(16)

式中：Vor(T′,v′,t′)为磨损经验模型；εV为误差随机变量，εV～N(0.09，0.032)。

对于上述工况参数，根据式(10)和式(16)得到柔轮内壁随工作时间变化的磨损曲线，如图9所示。图中虚线为磨损经验模型计算值，实线为修正后的磨损模型计算值。

2.2 柔轮变形模型

柔轮在传动过程中发生着柔性变形，由文献[12]可知，谐波齿轮传动误差由纯分量和扭转柔性分量两部分组成，而且柔性分量是传动误差高频分量的主要来源。结构柔性是影响传动精度的重要原因之一，而柔轮变形是导致结构柔性变形的主要原因[14]。

2.2.1 柔轮变形传动试验

在谐波齿轮传动中，柔轮变形是一个多因素耦合影响的动态过程，目前还没有准确表达柔轮变形的公式。本文通过搭建谐波齿轮传动试验平台(如图10)，开展谐波齿轮传动试验来研究柔轮变形的规律，采用柔轮杯口处的最大径向位移量B(单位：mm)表征柔轮变形程度，最大径向位移量指柔轮在传动过程中的最大变形量减去柔轮与波发生器装配后的最大圆半径。柔轮变形试验中，采用基恩士型号IL-S065激光位移传感器对谐波齿轮柔轮杯口处的径向位移进行测量[26]，如图11所示。

结合谐波齿轮减速器实际传动的工况参数，采用均匀设计方法对柔轮变形试验进行设计，将额定转速(单位：r/min)划分为25，50，75，100，125，150，175，200，225，250，额定负载(单位：N·m)划分为5，10，15，20，25，30，并对每组方案进行3次重复试验。

根据设计试验方案改变工况参数负载T和输入端转速v，得到谐波齿轮柔轮的最大径向位移量B，如图12所示，可见谐波齿轮柔轮杯口处的最大径向位移会受工况参数影响。

2.2.2 柔轮变形预测模型

由于谐波齿轮传动试验成本高，不能全面获取柔轮变形数据。再次采用GP回归模型预测柔轮杯口处的最大径向位移量，将试验数据对应的负载T和输入端转速v作为输入量I=(T,v)，柔轮杯口处的最大径向位移量B作为输出量构建训练样本，得到训练样本输入值I和预测样本输入值I′=(T′,v′)的联合高斯分布

(17)

式中：B为训练样本输出值；B′为预测样本输出值；kB(I,I)为训练样本的方差；kB(I,I′)为训练样本与预测样本的协方差矩阵；kB(I′,I)为预测样本与训练样本的协方差矩阵；kB(I′,I′)为预测样本的方差。

同理得到柔轮动态变形预测模型

(18)

为验证所建立的柔轮动态变形预测模型的准确性，在谐波齿轮输出负载T=17.5 N·m时，对比最大径向位移量B的预测均值和实测值，如图13所示。图中，黑色线为最大径向位移量预测均值，阴影区域为95%置信区间， 3组点为相同工况下最大径向位移量的实测值，实测值均位于95%置信区间内，因此可以采用该模型预测柔轮变形的最大径向位移量。

3 传动精度可靠性分析与优化设计

3.1 传动精度可靠性分析

根据综合建立的柔轮磨损模型、柔轮变形模型和传动误差模型，本节将对谐波齿轮传动精度进行可靠性分析。根据式(9)，建立考虑磨损与变形的谐波齿轮传动精度可靠性的功能函数

(19)

当Δθout-θal>0时，谐波齿轮传动处于失效状态，其传动精度可靠性表示为

P=1-Pf=1-P(g(a,θal)>0)。

(20)

式中Pf为齿轮传动的失效概率。

各误差项、磨损因素和变形因素均为服从正态分布的不确定性随机变量[3，25]，其中磨损因素和变形因素通过模型可由参数a=(T,v,t)表征。结合式(9)，谐波齿轮传动误差的数据样本可表示为K(a,Δθ)，其中a为样本输入量，Δθ为样本输出量。本文采用LHS试验设计方法[27-28]选择训练样本，将样本中的设计变量t分为j个区间量，并将每个时间量中的工况参数划分为i个小区间，数据样本表示为

(21)

数据样本的每个量中有b个子样本。抽样过程简化为在每个小区间内的b个样本点中随机等概率抽取一个样本点，并对i个随机得到的样本再次进行随机排列，形成一个j×i的样本矩阵，根据样本量从中随机选取样本作为训练样本，记为K′(a,Δθ)。

Kriging模型为一种半参数化插值模型，其通过对目标点周围信息加权来预测该点的响应[29]，本文采用Kriging模型对谐波齿轮传动精度进行可靠性分析。采用训练样本对Kriging模型[30]进行训练，模型输出量

J(w)=Kriging(w,K′(a,Δθ))。

(22)

式中w=(Tx,vx,tx)为输入量。

针对每一时间点的谐波齿轮工作情况，采用蒙特卡洛法[31]对输入变量进行N次抽样，将抽样所得的样本代入模型输出结果，传动精度可靠度可表示为

(23)

式中：N为抽样样本量；n为样本中的失效次数。

以第2章的某型号谐波齿轮为例，其误差项及相关公差取值如表3所示，采用上述可靠性计算方法求解某工况下谐波齿轮减速器的可靠度。

设定工况参数(负载T=17.5 N·m，输入端转速v=100 r/min)，根据本节的可靠性计算方法计算得到谐波齿轮传动精度可靠度曲线，如图14所示。在谐波齿轮工作时间t=3 000 h时，传动精度可靠度下降到91.17%。

3.2 传动精度可靠性优化设计

针对3.1节中谐波齿轮传动精度可靠性偏低的问题，需要对其进行可靠性优化设计，以提高传动精度可靠度。在齿轮加工过程中，误差公差值的大小与加工成本相关，不同公差值对应不同的加工精度等级，误差参数公差值缩小表示齿轮加工成本增加。本文对各项误差参数进行灵敏度分析，选取合适的误差参数作为设计变量，以总加工成本最低为目标函数，将传动精度可靠性、磨损量作为约束条件进行谐波齿轮传动精度可靠性优化设计，通过合理分配各项误差参数的公差值，在满足可靠性要求的同时，使加工成本降到最低。

表3 误差项及其公差取值 μm

3.2.1 影响因素灵敏度分析

第1章综合分析了影响谐波齿轮传动精度的因素，各项误差参数如表3所示。考虑到误差参数的数量较多，为减少优化设计变量数，提升优化设计效率，需要对各误差参数进行传动精度灵敏度分析，选取合适的误差参数作为设计变量，影响谐波齿轮传动精度的各误差项表示为

Δe=(Δff1,Δff2,ΔFp1,ΔFp2,eCS11,
eCS12,eFS11,eFS12,eWG11,eWG12,eWG21,eWG22)。

(24)

对影响传动精度的各误差项进行灵敏度分析，并做如下归一化处理：

(25)

(26)

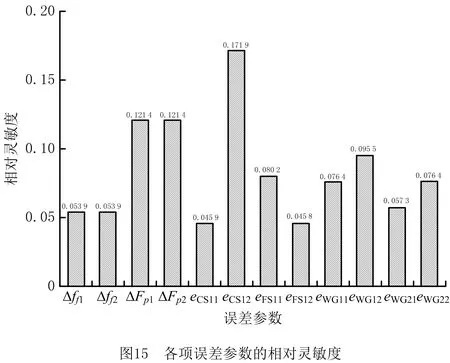
图15所示为谐波齿轮各项误差参数在传动精度的相对灵敏度分析结果。图中，ΔFp1，ΔFp2，eCS12对谐波齿轮的传动精度影响显著，Δff1,Δff2,eCS11,eFS12,eWG21对谐波齿轮的传动精度影响较小。

3.2.2 传动精度可靠性优化设计模型

(1)确定设计变量

通过分析影响谐波齿轮传动精度各误差项的灵敏度，得到3个灵敏度较大和5个灵敏度较小的影响因素，将影响因素ΔFp1,ΔFp2,eCS12,Δff1,Δff2,eCS11,eFS12,eWG21作为设计变量。

(2) 建立目标函数

在谐波齿轮的制造过程中，不同制造加工精度会产生不同的加工成本，本文将谐波齿轮中8个误差项的总加工成本C(Δe′)作为目标函数，

(27)

式中：j表示不同的成本函数；e′i表示某个优化设计变量。

尺寸公差成本函数C1、位置度公差成本函数C2和跳动公差成本函数C3[32]分别表示如下：

(28)

式中：Ze′i为某个优化设计变量的公差值；ae′i,be′i,ce′i,de′i,ee′i为对应函数的相对成本系数，ae′i=16.140,be′i=0.324,ce′i=0.217,de′i=0.013,ee′i=2.845。

(29)

式中:fe′i,ge′i,he′i,le′i为对应函数的相对成本系数，fe′i=4.862,ge′i=0.483,he′i=0.877,le′i=1.020。

C3(Δe′i)=me′ie-se′iZe′i。

(30)

式中:me′i,se′i为对应函数的相对成本系数，me′i=23.729,se′i=0.682。

(3) 建立约束条件

将谐波齿轮的传动精度可靠度作为约束条件，在齿轮工作到预期工作时间时可靠度仍符合规定，即

P=P(Δe′)(T, v, t)=
[1-P(g(K′(T,v,t))>0)]≥Pre。

(31)

式中：P(Δe′)(T,v,t)为对设计变量进行优化得到的对应的可靠度，Δe′为优化设计变量，(T,v,t)为工况参数；Pre为规定的最小传动精度可靠度。

将柔轮和柔性轴承的磨损量作为约束条件，即

V(Δe′,(T,v,t))=Vac-Vpre≤0。

(32)

式中：Vac为实际磨损量；Vpre为规定的最大磨损量。

综合目标函数和约束条件，得到谐波齿轮传动精度可靠性优化设计数学模型：

s.t.

(33)

式中:δmax，δmin为优化参数的最大值和最小值。

3.2.3 优化设计算例

以第2章的谐波齿轮减速器作为对象，采用序列二次规划法[33]求解3.2.2节得到的优化设计模型。设计变量误差项的公差取值范围如表4所示，取相同的工况参数，通过优化设计方法得到最终的设计变量，表5所示为优化前后的设计变量公差值。

表4 设计变量误差项的公差取值范围 μm

表5 设计变量公差优化前后的值 μm

谐波齿轮优化后，其加工成本从319.221 8元上升至324.654 7元，相对增加了1.70%。根据优化后的结果，获得谐波齿轮的传动精度可靠度，如图16所示。可见，优化后的谐波齿轮传动精度可靠性有显著提升，在工作时间t=3 000 h时传动精度可靠度达到99.02%，比优化前提升7.85%。经可靠性优化设计后，在加工成本小幅度增加的前提下，谐波齿轮的传动精度可靠性出现大幅提升，满足传动精度可靠性的要求，实现了可靠性优化设计。

4 结束语

本文针对谐波齿轮传动误差模型难以准确反映谐波齿轮实际工作情况的问题，分析了谐波齿轮存在的加工装配误差，并考虑柔轮磨损和变形带来的误差，建立了考虑磨损与变形的谐波齿轮传动误差模型。

通过对磨损和变形因素展开研究，在柔轮内壁和柔性轴承摩擦磨损方面，应用贝叶斯修正方法修正磨损经验模型，使修正后的模型更加符合实际磨损情况。针对柔轮变形因素，考虑柔轮变形随工况参数变化的情况，根据试验数据和高斯过程回归建立高精度的柔轮变形模型。

综合获得的谐波齿轮传动误差模型、磨损模型和变形模型构建精度可靠性模型，采用基于LHS方法的Kriging模型建立了可靠性分析代理模型，同时采用蒙特卡洛法求解谐波齿轮某工况下的传动精度可靠度。结果显示，齿轮传动精度可靠度前期下降平缓，当工作到一定时间时，可靠度下降明显，直到无法满足传动精度要求。

将误差项参数作为设计变量，建立了以加工成本最低为目标函数、传动精度可靠性和磨损量为约束条件的优化设计模型，并采用序列二次规划法进行优化。算例表明，优化后的谐波齿轮在加工成本小幅度增加1.70%的前提下，其传动精度可靠性大幅度提升，在工作时间为3 000 h时，可靠度相比优化前提升7.85%，达到99.02%。