基于可伸展变形的双稳态圆柱壳计算模型
张 征,虞筱琛,孙 敏,吴化平,姜少飞
(浙江工业大学 机械工程学院,浙江 杭州 310014)
0 引言
碳纤维复合材料层合结构有两种不需要外力维持的稳定构型,同时拥有力学性能优异、轻质、高强等一系列特性,在智能可变形、能量收集、仿生及其他领域具有广泛的应用前景[1]。
目前根据初始构型,国内外研究中的双稳态复合材料层合结构主要分为平板型和圆柱壳型。平板型复合材料层合结构主要由特殊正交铺设的层合板在平板型模具上经高温、高压固化后,自然冷却至室温得到[2];圆柱壳型复合材料层合结构主要由反对称铺设的层合板在圆柱形钢制模具中保压固化并冷却至室温后得到[3]。两种类型的双稳态复合材料层合结构呈现的双稳态特性均为比较规则的圆柱形,区别在于平板型非对称正交铺设层合板所示的两种稳态具有不同的曲率方向,而圆柱型反对称铺设圆柱壳所示的两种稳态具有相同的曲率方向。其中对平板型复合材料层合结构的研究比较集中,基于瑞利里兹法,DANO等[2]提出一个经典的14参数理论模型;PIRRERA等[4]建立了最高达11阶的高阶理论模型,通过无量纲化处理并采用路径跟随算法求解非对称铺设层合板的稳态构型。对于圆柱型复合材料层合结构,GUEST等[5]提出一种双参数模型,也称不可伸展变形均匀曲率模型(Inextensible Uniform Curvature Model,IUCM),用于复合材料圆柱壳的不同稳态构型;文献[6-8]在考虑温度、湿度等因素对圆柱壳双稳态特性的影响下,研究几何参数的影响,同时提出两点加载法探究两种稳态构型之间的突变载荷;吴耀鹏等[9]和杨留义[10]也对双稳态圆柱壳结构进行了相应研究。上述复合材料圆柱壳的理论模型均基于经典层合板理论和不可伸展变形假设,即假设层合圆柱壳各处变形一致且其第二稳态构型仍为圆柱形。SEFFEN[11]基于可伸展变形假设,综合考虑拉伸应变能和高斯曲率,提出可伸展变形均匀曲率理论模型(Extensible Uniform Curvature Model,EUCM),系统地探究初始曲率与材料属性对结构双稳态特性的影响;VIDOLI等[12]对SEFFEN的模型进行了改进,发现了第3种稳态构型,并进行了定性讨论。
除了理论模型,利用有限元模拟分析也能够有效预测复合材料圆柱壳的双稳态特性,然而当圆柱壳的材料参数或几何参数发生改变时,往往需要改变其有限元模型,重复的手工操作需花费大量时间,降低了仿真效率。同时,手工操作产生的模型可能存在差异,导致仿真结果出现误差。目前,双稳态圆柱壳主要通过手动建模的方法分析参数,尚无有关其参数化建模及后处理的文献报道。从软件开发的角度,有限元仿真工具的二次开发需考虑可扩展性和实用性[13]。
因此,面向复合材料圆柱壳提出基于可伸展变形均匀曲率模型的简化理论模型,并基于Abaqus二次开发功能建立了复合材料圆柱壳双稳态特性分析插件,实现了其快速、参数化建模与自动后处理;其次,利用理论和有限元模型对影响复合材料圆柱壳双稳态特性的因素进行分析;最后通过实验验证了所提设计模型的有效性和准确性。
1 理论模型
通过建立复合材料圆柱壳的理论模型求解稳态曲率来判断其是否具备双稳态特性,通常将圆柱壳的第二稳态主曲率作为评价圆柱壳双稳态特性的指标。为便于分析,在研究圆柱壳双稳态特性时作如下假设:①圆柱壳为薄壳结构,满足直法线假定;②圆柱壳处于平面应力状态,中面无应变,且任意时刻中面内各点的曲率均相同;③复合材料为理想线弹性材料;④圆柱壳曲率均匀变化。
基于可伸展变形假设,可将总势能U表示为仅与曲率相关的无量纲表达式,其为弯曲应变能(第1项)和拉伸应变能(第2项)之和[12],即
(1)
(2)

K=R0k,H=H0+Hi=R0(h0+hi)。
(3)
式中:k为计算的曲率矩阵;h为初始曲率矩阵,分为初始自然曲率h0和初始非弹性曲率hi,初始无量纲高斯曲率仅与初始自然曲率有关,初始非弹性曲率由温度、湿度等引起的非弹性变形产生;下标x,y,xy分别表示两个方向的曲率和扭曲率,壳结构的初始曲率和几何参数的定义如图1所示。R0为无量纲系数,
(4)
式中:S为壳体的俯视面面积;t1为壳体的等效厚度;ψ为拉弯系数,用于衡量拉伸应变能与弯曲应变能之间的比例,仅与拉伸刚度矩阵和俯视面形状有关,
(5)
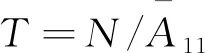
(6)
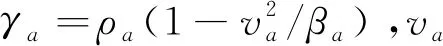
(7)
式中:div,curl分别为散度和旋度运算;n为边界处的法线,为二阶对称张量形式。偏微分方程(7)实际上是一个标准平面弹性问题,divTk和-Tkn分别表示平面受到的体力和剪切面力。采用自动求解偏微分方程的软件FEniCS[14]计算偏微分方程(7),可得Th,而Tk为满足偏微分方程的近似函数。

当不考虑初始非弹性曲率时,即圆柱壳的初始曲率为Hy=H0,代入式(1)后,根据最小势能原理可得方程组∂U/∂K=0,稳态曲率的平衡解通过求解下式获得:
(8)
所得平衡解还需要通过稳定性判断,即满足海塞矩阵∂2U/∂2K的正定性,代入圆柱壳后简化为:
2γd-KxKy>0。
(9)
当考虑初始非弹性曲率时,即圆柱壳的初始曲率为Hy=H0+Hi,首先通过经典层合板理论得到初始非弹性曲率[7]
(10)
式中:εi,ki,Ni,Mi表示由温度或湿度产生的应变、曲率、内力和内力矩。特别地,对于反对称铺设的壳结构,温度或湿度主要导致扭曲率发生变化,x,y方向的曲率的变化可以忽略不计。将得到的初始非弹性曲率代入式(3)进行无量纲化,随后将初始曲率代入式(1),因为其无法得到简便的数学表达式,所以根据上述过程直接采用数学计算软件(如MATLAB)得到稳态曲率。
2 仿真模型
本文所研究的复合材料圆柱壳二次开发分为两部分:①参数化建模,包括建立几何模型、赋予材料属性、装配模型、设置边界条件和接触条件、划分网格,其中参数化建模包括稳态突变的两个过程,snap-through表示初始构型至第二稳态构型,snap-back表示其逆过程;②自动后处理,包括稳态构型、稳态曲率和载荷位移曲线的输出。整体流程如图2所示。

2.1 参数化建模
本文基于两点加载法[7]建立复合材料圆柱壳的仿真模型(如图3),模型由圆柱壳、支撑平板和压头3部分组成,且与实际的实验环境相同。

图3中压头根据实际尺寸简化为半径为5 mm的半圆柱刚体,长L=100 mm,支撑平板简化为长、宽均为100 mm的刚性板,两平板之间的距离参照实际间距,压头与圆柱壳的初始间距为10 mm。圆柱壳有矩形和椭圆形两种,其中椭圆圆柱壳的俯视面为椭圆形,通过裁剪矩形圆柱壳得到,其几何参数由圆心角γ、纵向长度L和初始曲率h0定义,与理论模型的几何参数关系有b=2sin(γ/2)/h0,a=L/2。圆柱壳的材料属性和铺层设置采用一般复合材料设置方法,E1和E2为单层板在材料主方向上的弹性模量,G12为单层板在材料1-2平面的剪切弹性模量,v12和v21为泊松比,因为假设复合材料为横向各向同性,所以有G12=G13=G23。模型采用S4R单元对圆柱壳进行划分,通过设定线段数目(number)或网格尺寸(size)调整网格数目。整体的边界条件设置包括温度场变化、平板间距和压头位移。模型建立了3个静态分析步,求解方法为完全牛顿法,分析步设置如下:
(1)温度变化过程 分析温度对复合材料圆柱壳双稳态特性的影响,可以通过等效热膨胀系数分析湿度对复合材料圆柱壳双稳态特性的影响[7]。该步需要开启非线性大变形选项,同时开启自动稳定功能,按照默认的参数采用伪动态的非线性计算使结果更容易收敛。
(2)加载过程 对压头施加适当的位移载荷,支持平板完全约束,圆柱壳的中心点仅放松对z方向位移的限制。
(3)卸载过程 将压头移回原位而其余均不变,可得突变至第二稳态的复合材料圆柱壳。
根据以上步骤中的参数,设定用于Abaqus二次开发的关键词,如表1所示。
由此开发了相关的插件界面,如图4所示。通过输入相关参数,能够建立矩形或椭圆圆柱壳双稳态特性分析的snap-through有限元模型。经过设置重启动,可将突变至第二稳态的圆柱壳重新导入新的模型中,重复设置上述装配、边界条件和接触条件,得到snap-back有限元模型。

表1 关键词设定

2.2 自动后处理
当snap-through和snap-back有限元模型均计算完成后,通过Python脚本能够直接读取odb.文件中的数据。针对复合材料圆柱壳双稳态特性,需要得到其两个稳态构型、稳态曲率及两种稳态互相转化过程中的载荷信息,即载荷位移曲线,从而得到其突变载荷。其核心代码和程序如下:
for i in range(number_nodes): #根据节点数量循环得到坐标
808 Influencing factors of treatment compliance to automatic continuous positive airway pressure for obstructive sleep apneahypopnea syndrome
xyz0=nn[i].coordinates
initial_labels.append(nn[i].label) #得到节点编号
initial_xyz.append(list(xyz0))
#获得Step-3中的最后frame信息
frames=o.steps[o.steps.keys()[-1]].frames[-1]u=frames.fieldOutputs['U'] #获得位移信息
fsk=frames.fieldOutputs['SK'] #获得曲率信息
for i in range(number_element):
fsk1=fsk.values[i].data[0]
sumsk1=sumsk1+fsk1
finalsk1=sumsk1/number_element
…
for i in range(len(o.steps[stepname].frames)):
u2=o.steps[‘Step-2’].frames[i].fieldOutputs['U'].values[indentnumber].data[1] #获得压头位移信息
rf2=o.steps[‘Step-2’].frames[i].fieldOutputs['RF'].values[indentnumber].data[1] #获得压头支反力信息
…
3 参数分析
利用插件能够方便地进行参数分析,同时通过制备相应的试件验证上述理论模型中简化后的EUCM以及有限元仿真插件的准确性,本文进行了矩形及椭圆形双稳态复合材料圆柱壳的相关实验。实验所用复合材料的材料属性如表2所示,其中t为单层材料的厚度。实验样本如图5所示,具体参数如表3和表4所示。
表3中,字符串“C-h0-α-p-t-a-b-L-γ”描述不同规格试件,其中:C表示圆柱型层合结构;h0表示初始自然曲率,默认圆柱壳的初始曲率为hx=hxy=0,hy=h0,单位为m-1;α为铺设角度,单位为(°);p为铺层数,若p为奇数(如p=5),则铺层方式为[α/-α/0/α/-α],若p为偶数(如p=4),则铺层方式为[α/-α/α/-α];t表示单层复合材料的厚度,单位为10-2mm;a,b表示尺寸参数,单位分别为mm,10-2mm;L为纵向长度,单位为mm;γ为圆心角,单位为(°);样本编号中RP表示矩形试样,EP表示椭圆形试样。

表2 T700/3234单向层合板的材料属性
复合材料圆柱壳的双稳态特性与其几何参数、铺层方式和温度相关,下面通过对比IUCM与EU-CM的理论预测结果和模拟结果探究各参数对第二稳态主曲率kx2的影响,以及温度对第二稳态扭曲率kxy2和最大突变载荷的影响。


表3 双稳态复合材料矩形圆柱壳实验样本

表4 双稳态复合材料椭圆形圆柱壳实验样本
3.1 几何参数分析
复合材料圆柱壳的几何参数包括圆心角γ、纵向长度L和初始曲率h0。在保持铺层参数不变的同时,即p=5,α=45°,通过单变量控制研究几何参数对圆柱壳双稳态特性的影响。
圆心角对圆柱壳双稳态特性的影响如图6所示,保持不变的几何参数为L=100 mm,h0=0.04 mm-1;纵向长度对圆柱壳双稳态特性的影响如图7所示,保持不变的几何参数为γ=180°,h0=0.033 mm-1;初始曲率对圆柱壳双稳态特性的影响如图8所示,保持不变的几何参数为γ=180°,L=100 mm。图中分别展示了IUCM、EUCM、有限元仿真分析(Finite Element Analysis,FEA)以及Experiment(试验)的相应结果。
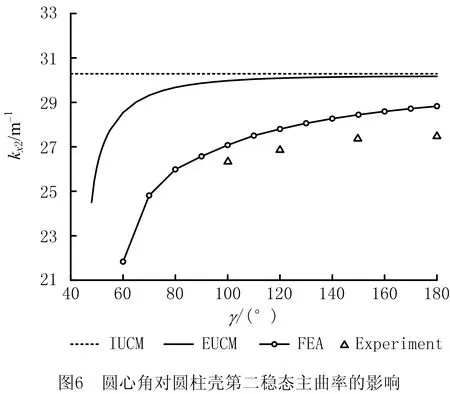
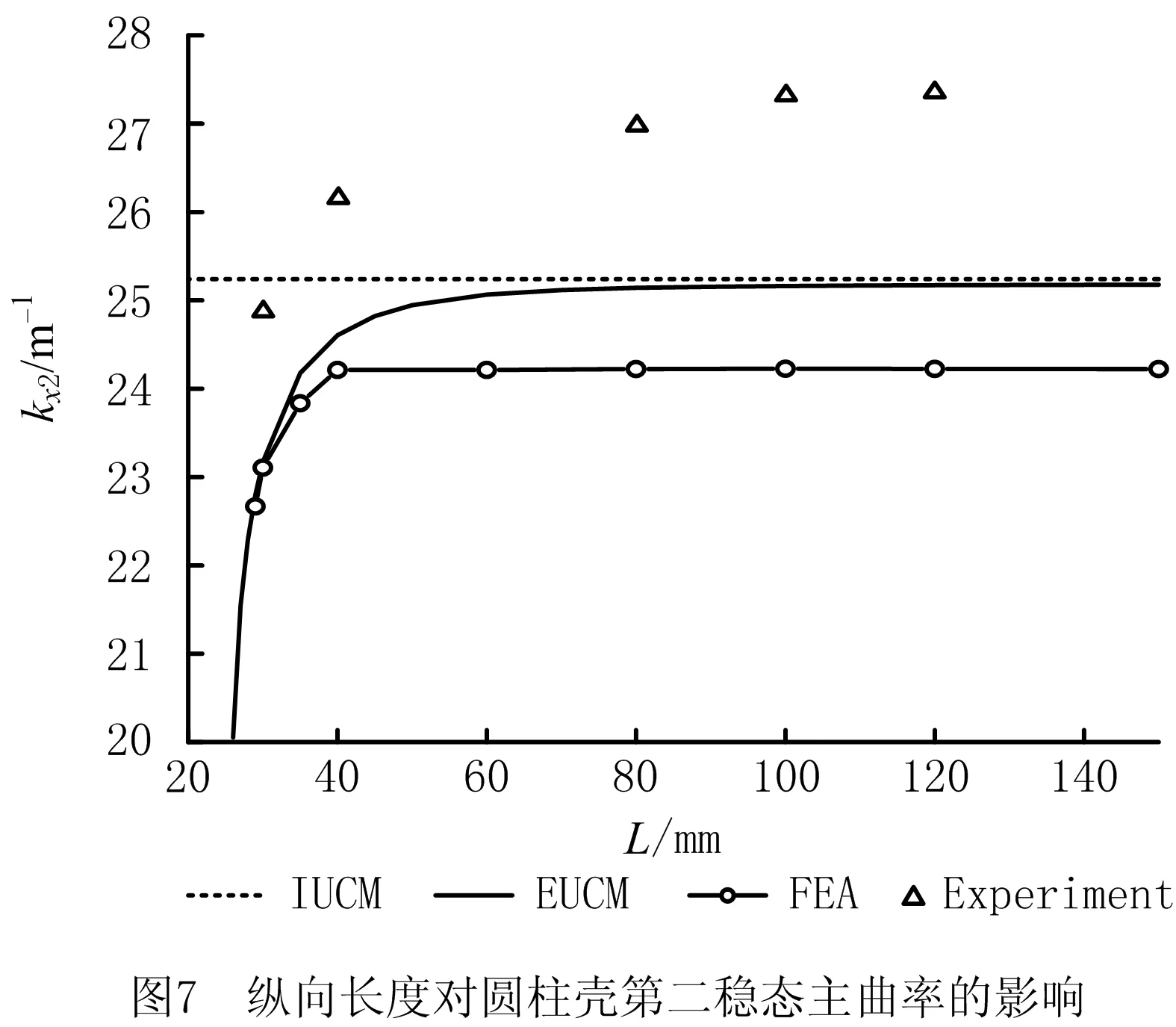
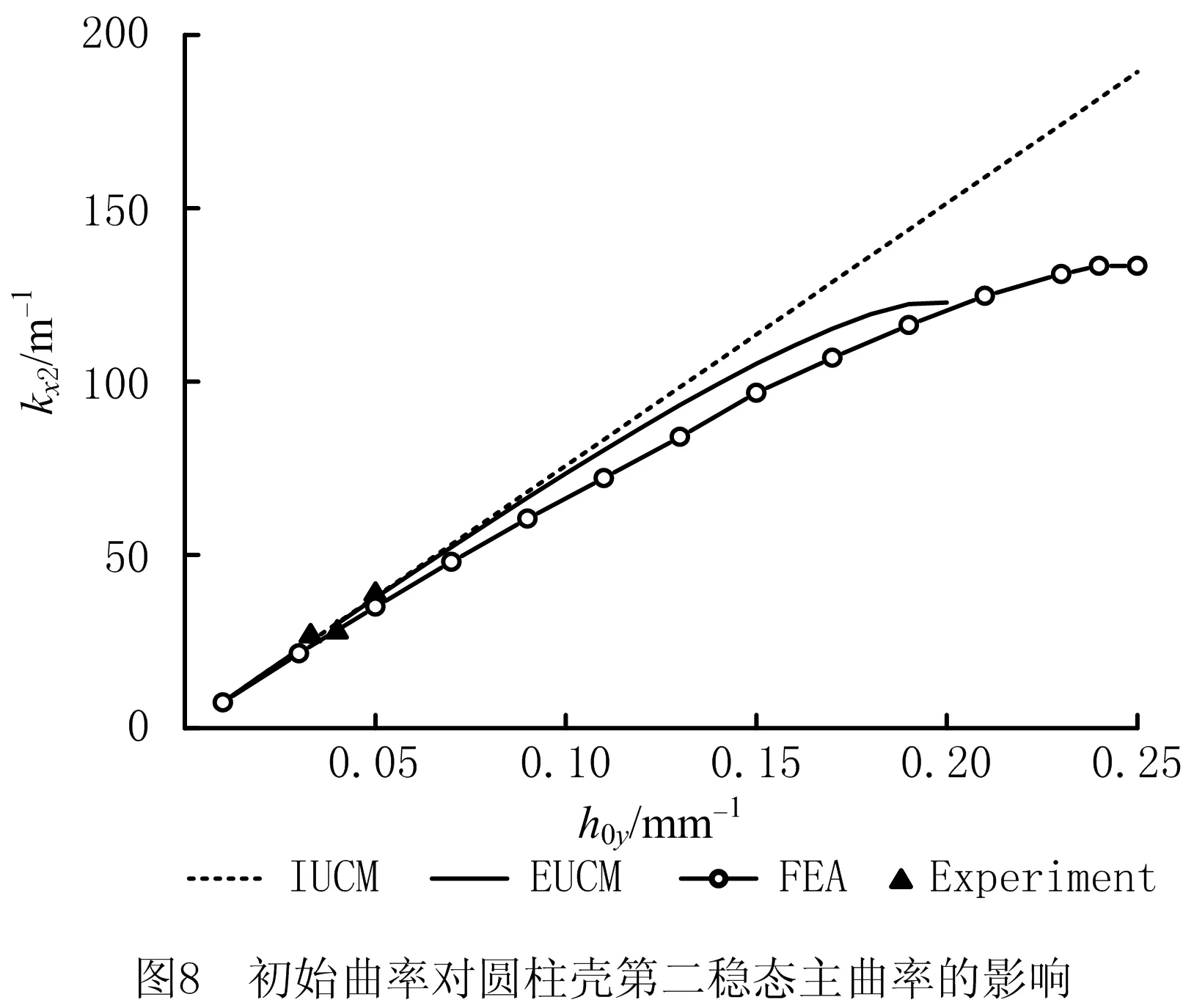
由图6~图8可知,IUCM预测第二稳态主曲率不随圆心角和纵向长度变化而变化,随初始曲率增加而线性增长。相反,简化EUCM能预测第二稳态主曲率随各参数变化的趋势,且与模拟结果吻合,即第二稳态主曲率均随圆心角、纵向长度和初始曲率的增加而增加,且其双稳态消失的趋势一致。但EUCM对双稳态临界值的预测结果与模拟结果有一定误差,图6~图8中EUCM预测的双稳态临界值为γ=50°,L=26 mm,h0=0.20 mm-1,而模拟所得的临界值为γ=60°,L=29 mm,h0=0.25 mm-1,误差来源于理论模型中的简化假设。除此之外,第二稳态主曲率的实验结果与模拟结果和EUCM理论预测结果吻合,误差在10%以内。
3.2 铺设参数分析
复合材料圆柱壳的铺设参数包括铺设角度α和铺层数p。在保持几何参数不变的同时,即γ=180°,L=100 mm,h0=0.04 mm-1,通过单变量控制研究铺设参数对圆柱壳双稳态特性的影响。铺设角度对圆柱壳双稳态特性的影响如图9所示,保持不变的铺设参数为p=4;铺层数对圆柱壳双稳态特性的影响如图10所示,保持不变的铺设参数为α=45°。

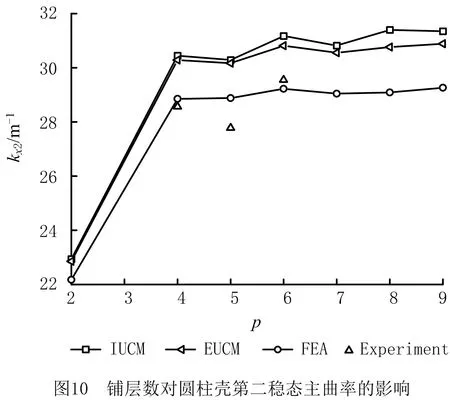
由图9和图10可知,IUCM和简化EUCM预测的第二稳态主曲率随铺设参数的变化趋势一致,其随铺设角度的增加而增加,而随着铺层数的增加,主曲率可能会减小或增加,展示出奇偶性变化。主要原因是不同铺层下的材料刚度矩阵不同,具体体现在其拉伸和弯曲刚度矩阵上。当铺层数为偶数时,所得无量纲化的拉伸和弯曲刚度矩阵不变;当铺层数为奇数时,所得无量纲化的拉伸和弯曲刚度矩阵比偶数时小,且随层数增加呈增大的趋势。因此,无论理论、模拟还是实验,所得结果随铺层数的改变均呈现一个交替变化的过程,实验结果、模拟结果和理论结果的误差在10%以内。
当圆柱壳的形状为椭圆时,理论、模拟、实验结果如表5所示,其中上标a,f,e分别表示理论、模拟、实验结果。对比表5中EP1~EP6的理论、模拟、实验结果可以发现,第二稳态主曲率随着圆心角、纵向长度、初始曲率和铺设角度的增大而增大,规律与矩形圆柱壳相同。

表5 双稳态复合材料椭圆形圆柱壳第二稳态主曲率结果
3.3 温度分析
考虑复合材料圆柱壳受温度的影响,同时材料属性与温度相关,根据测试数据[7]拟合可得材料属性与温度的关系:
E1=(-1.054×10-7e0.213 3T+110e-0.000 934 4T)×
106MPa;
E2=(31.54e-0.109T+3.73e-0.003 17T)×106MPa;
G12=-2.729×10-5T3+0.004 038T2-0.222 8T+8.23 MPa;
v12=0.31;
α1=(1.25×10-4T2+0.002 5T-2.2)×10-6;
α2=(1.077×10-4T3-0.015 51T2+0.457 7+60.52)×10-6。
(11)
试件的几何参数为圆心角180°,纵向长度100 mm,初始曲率0.04 mm-1;铺层方式为[45°/-45°/45°/-45°],单层厚度为0.12 mm。利用附带温控箱的拉伸试验机平台模拟环境温度,通过加载使圆柱壳发生稳态突变,从而得到其最大突变载荷,如图11所示。通过数字图像处理技术获得试件的曲率信息,具体参见文献[7]。

模拟中需输入的参数已在图4给出,最终得到的实验、模拟、理论结果如表6所示。结果表明,三者变化趋势一致,均随温度的增加而不断增加。主曲率的理论和模拟结果的相对误差在10%以内,然而测量所得实验结果偏大,可能的原因有:①实际测量误差;②实际材料属性与模拟和理论中输入的材料属性有一定误差。然而三者对扭曲率的预测结果比较吻合。
试件的最大稳态突变载荷模拟与实验结果对比如表7所示,其中下标t,b分别表示snap-through和snap-back模型。可知,snap-through的稳态突变载荷随温度上升而减小,snap-back则相反,实验

表6 圆柱壳第二稳态主曲率kx2与扭曲率kxy2随温度变化的情况
与模拟结果趋势相符。snap-through过程的实验和模拟结果误差较大,原因可能是模拟过程的加载位移远大于实验中所施加的位移,使模拟中压头受到的支反力偏大。snap-back过程的实验和模拟结果的误差相对较小。
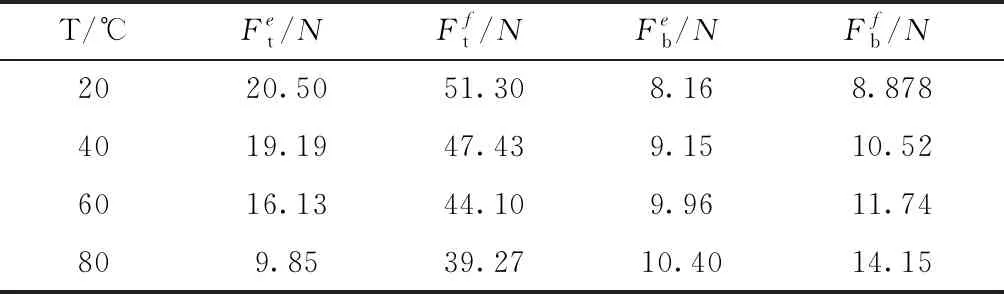
表7 圆柱壳最大稳态突变载荷对比
4 结束语
本文基于可伸展变形假设和均匀曲率模型,提出一种适用于复合材料圆柱壳双稳态特性分析的简化计算模型。该模型与现有IUCM相比适应性更好,预测精度更高,而且相比IUCM,能分析不局限于矩形的其他形状双稳态圆柱壳的稳态特性。同时利用Python语言,根据Abaqus二次开发功能建立了用于复合材料圆柱壳双稳态特性分析的参数化建模和自动后处理插件。最后,通过实验验证了理论和仿真结果的准确性,三者预测的稳态曲率和最大稳态突变载荷的变化规律相同,验证了所提计算模型的可行性。下一步将对更多不同形状的圆柱壳进行双稳态特性分析,并开展结构优化及其在仿生智能可变形结构中的工程应用研究。

