“长方形、正方形面积的计算”教学实践与思考

芦建章

[摘 要]“长方形、正方形面积的计算”是学生学习面积计算的起始课，需要在引导学生理解知识、掌握方法的同时，发展他们的空间观念。文章在对教材、学情、传统教法分析的基础上，通过创设有效的情境，引导学生操作、观察、思考、辨析，初步发展他们的空间观念。

[关键词]操作;空间观念;面积计算;长方形与正方形

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2022）02-0066-03

“长方形、正方形面积的计算”是人教版教材三年级下册的内容，也是学生系统学习面积计算的起始课。笔者在教学这一内容时，做了如下分析与尝试，取得了较好的教学效果。

一、对教材、学情与传统教学的解读

1.对教材的解读

关于“长方形、正方形面积的计算”，人教版教材中的例题分为三个层次：

层次一：通过画格子和摆面积单位测量长方形面积的活动，在“数面积”的基础上初步得到长的块数与宽的块数之积就是长方形的面积。

层次二：在提出猜想的基础上，通过用1平方厘米的正方形拼成不同的长方形，观察、思考长方形的面积与长、宽的关系，进而用不完全归纳法得出长方形面积的计算方法。

层次三：通过测量、计算长方形、正方形的面积，在进一步巩固长方形面积计算方法的同时，推导出正方形面积的计算方法。

通过对教材的分析，可以得出：由于学生是第一次学习面积的计算，之前没有面积计算的知识储备，因此借助“铺面积”的活动经验，引导学生通过摆一摆、数一数，得到长方形的面积，进而引导学生发现每行摆的个数乘摆的行数，正好是长方形的面积。在此基础上提出猜想并通过验证，进一步揭示长方形面积的计算公式。这样的编排体系，遵循了知识的发生、发展的逻辑过程。

2.对学情的解读

学生在学习本课之前，刚刚学习了面积的意义与常见的面积单位，但对如何计算面积没有知识方面的储备，不能像学习平行四边形、三角形等图形面积时，用“转化”的思想方法，把新知轉化成旧知，进而推导面积计算公式。因此，在学习方法上是“无法可依”的，完全是“零基础”。鉴于此，教师在教学时，只能立足于原始的摆面积单位的活动，帮助学生初步积累活动经验，以此为知识的生发点进行后续的学习。在此过程中，学生的观察、猜想、归纳、概括等能力得到了初步的培养与发展，为后续学习相关知识积累了非常重要的经验。

3.对传统教学的解读

在传统的教学中，教师往往引导学生用1平方厘米的小正方形铺长5厘米、宽3厘米的长方形，从而发现长边正好可以铺5个、宽边正好可以铺3个，5与3的乘积是15，正好是1平方厘米的小正方形的使用个数，说明长方形的面积是15平方厘米，从而猜想“长方形的面积=长×宽”，随后通过验证、练习来巩固这一公式。这样的教学，虽然可以让学生掌握长方形面积的计算方法，但也会带来以下弊端：

第一，重方法轻过程。传统的教学中，教师往往注重引导学生以掌握、应用公式，以及会计算面积为目标。在这样的教学思想的引领下，学生只记住了计算方法，到五年级再次学习平面图形的面积计算时，已经忘记了是如何推导长方形的面积计算公式的。

第二，忽视对学生空间观念的培养。本课内容属于“图形与几何”领域，因此，它在使学生理解和掌握知识、发展技能的同时，还承载了一个非常重要的隐性目标——培养与发展空间观念。传统的教学注重“双基”却忽略了这一目标，不利于学生空间观念的发展。

二、教学实践

基于以上思考，笔者在教学本课时做了如下尝试：

【教学片段一】初步感受面积的大小与长、宽有关。

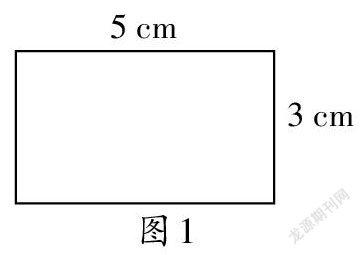
师（出示图1）：我们已经认识了面积，也知道了常用的面积单位。要知道这个长方形的面积是多少，你有什么办法？

生1：可以用1平方厘米的小正方形去摆摆看。

师：“摆摆看”是什么意思？

生1：就是用1平方厘米的小正方形铺在这个长方形里。

师：为什么你不用1平方分米或1平方米的正方形去摆呢？

生1：这个长方形太小了，用1平方分米的去摆就会把它盖住，更不要说用1平方米的了。

师：是啊，我们在选择正方形去摆的时候要考虑图形的大小。那就请大家用1平方厘米的小正方形去摆摆看它有多大。（学生动手操作，教师巡视）

师：你是怎么摆的？

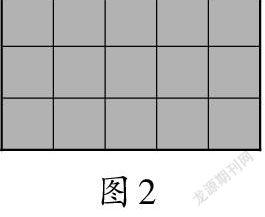
生2：一行摆了5个，摆了3行。（如图2）

师（追问）：一行为什么可以摆5个？为什么可以摆3行？

生2：长边长5厘米，小正方形的边长是1厘米，5厘米里面有5个1厘米，所以正好可以摆5个。宽边长3厘米，3厘米里面有3个1厘米，所以正好可以摆3个，也就是3行。

师：根据你的摆法，你知道这个长方形的面积是多少吗？你是怎样想的？

生2：是15平方厘米。我把这个长方形摆满正好用了15个小正方形，所以是15平方厘米。

师（小结）：像他这样摆的同学还有吗？（其他学生举手示意）像这样摆，正好用了15个1平方厘米的小正方形，所以得到这个长方形的面积是15平方厘米，真不错！

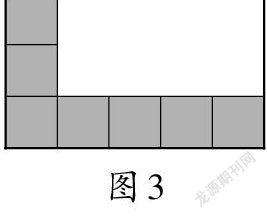
生3（举手）：老师，我还有不同的摆法。长边正好摆5个就是一行摆5个，宽边只摆了1列，是3个，说明可以摆3行。（如图3）不需要全部摆满，我也知道一共可以摆15个。

师：其他同学听明白了吗？

师（小结并用手势比画）：像他这样摆，一行摆了5个，一列摆3个，就可以知道整个长方形可以摆15个，真是个好办法！

【教学片段二】感悟长、宽的变化会引起面积的变化。

课件演示：

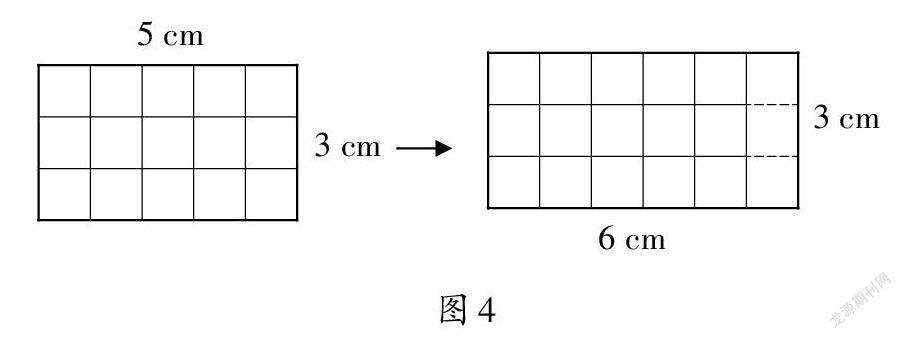
师：图4中，与原长方形面积比较，演变后的图形面积发生了什么变化？

生1：变大了。

师：为什么会发生这样的变化？大了多少？（学生观察）

生2：长变长了，所以面积变大了。大了3平方厘米。

师：明明长只增加了1厘米，为什么面积却增加了3平方厘米呢？

生3（指着图4）：宽是3厘米，虽然长只增加了1厘米，但对于长方形来说却增加了3个1平方厘米。

师：请想象一下，如果长方形的宽不变，面积要变小，要怎么办？（长缩短）

课件演示：

师：图5中，与原长方形面积比较，演变后的图形面积发生了什么变化？为什么会发生这样的变化？（长不变，宽增加1厘米，面积就增加5个1平方厘米）

师：请你想象一下，如果长方形的长不变，面积要变小，怎么办？（宽缩短）

【教学片段三】比较归纳，构建模型。

师：长方形面积的大小与什么有关？

生1：和它的长、宽都有关系。

师：你能根据刚才的学习说一说怎样计算长方形的面积吗？

生2：计算长方形的面积，只要用它的长乘宽就可以了。

（板书：长方形的面积=长×宽）

三、教学思考

“空间观念”是《义务教育数学课程标准（2011年版）》中的十个核心概念之一，同时也是数学素养的重要组成部分。课标中明确了其意义：根据物体特征抽象出几何图形，根据几何图形想象出所描述的实际物体;想象出物体的方位和相互之间的位置关系;描述图形的运动和变化;依据语言的描述画出图形;等等。如何在日常教学中，有效培养与发展学生的空间观念呢？笔者以为，空间观念的培养应贯穿“图形与几何”领域内容教学的始终。以本课为例，我们需要关注：

1.重视活动经验的积累与内化

从人的认知发展来看，要构建一个认知体系，其前提是需要有必备的知识与经验作为基础。借助已有的知识、经验并积累到一定“厚度”时，就能自然地生发新的知识点，获得全新的体验与认识，从而促使认知结构进行“自动化”重构，并为接下来的学习重构又积累了更高一级的基础，学习也就自然发生了。在这一过程中，经验的积累与内化是促进变化的关键因素。在本课中，笔者没有采用传统的“老师讲、学生练”的教学模式，而是设计了让学生“摆、想、说”等操作环节，从学生已有的知识尤其是经验入手，引导他们在摆的过程中初步感悟小正方形的块数与长方形面积之间的关系，以引发学生的思考。此外，通过对不同摆法的比较，学生在积累摆的活动经验的同时，也进一步明白了“面积”的意义。

2.引导学生从一维观念向二维观念过渡

在三年级上册，学生已经学习了长方形、正方形的周长，周长使用的是长度单位，属于一维观念。如何使学生的观念从一维进入二维呢？也就是要实现从“一维的线”到“二维的面”的突破。如果仅靠语言的描述是不可能达成目标的。因此，笔者把达成这一目标的任务渗透到了操作环节中。在初步感受面积的大小与长、宽有关的环节中，学生通过动手摆小正方形，逐步积累了经验。特别是第二种摆法，只摆一行和一列，就能计算出摆满整个长方形需要的小正方形的个数。通过强化这里的“行”与“列”，形成二维图像的雏形（横与纵），潜移默化地引导学生从一维观念到二维观念有效过渡。

3.引导学生认识面积的本质意义

在“计算面积”的教学中，学生往往只关注计算公式是否应用得当、计算结果是否正确，却不思考面积的本质意义。在本课中，结合摆小正方形的操作活动，使学生明白：用15个1平方厘米的小正方形正好可以把长方形摆满，长方形的面积就是15平方厘米，即长方形的面积是单位面积（1平方厘米）累积的结果，这才是面积的本质意义。在用小正方形去铺长方形时，学生通过调用已有的知识与经验发现：用1平方分米与1平方米的正方形都不合适。到此强化了学生对平面大小的判断能力，这也有助于学生空间观念的构建。

4.引导学生在变与不变中发展想象力

通过引导学生对图像“变”与“不变”的动态比较，发展学生的想象力，即在从物体中抽象出几何图形、想象图形的运动和位置的过程中发展空间观念。与静态图像相比，动态的图像更能引起学生的注意，刺激性更强，从而引发学生思考。因此，在初步感受长方形面积的基础上，笔者设计了长（宽）变、宽（长）不变的环节，让学生通过观察由于长度（一维）的变化而引起面积（二维）的变化，进一步认识面积的意义。同时引导学生想象“如果要使面积变小该怎么办”，以此促进学生空间观念的形成与发展。这一经验的积累，也有利于学生在后续学习体积的相关内容时，能够较好地从二维向三维过渡。

（责编 罗 艷）