多孔格栅均匀化模型平压仿真分析
盛亚鹏, 段玥晨, 谢 鑫
(郑州大学 机械与动力工程学院,郑州 450001)
1 引 言
格栅是一种轻型周期性结构,具有隔热、吸能和可设计性强等特点,在航空航天及高铁和汽车等领域有着广泛应用。王世勋等[1]对格栅的制备工艺、分析设计、性能测试及工程应用做了概述。李旌豪[2]对不同材料格栅结构进行了大量平压实验,探究了格栅夹芯板面内和面外的抗压性能。
在格栅力学性能研究中,常见的分析方法有实验分析和仿真分析两种。实验分析方法更加切合实际情况,但对某些大体积多层级格栅部件,实验分析难度大且成本高,往往需建立力学模型进行仿真分析[3]。对周期性格栅结构进行力学仿真分析时,为了减少运算量,可以从格栅周期性单胞尺度出发,推导其宏观性能[4,5]。现阶段的普遍方式是在单胞边界面建立绑定约束[6,7],但采用该方法会形成边界过约束。代表体元法(RVE)是一种在周期性结构中选取能代表整体特征的体积单元进行研究的方法。该方法过程简洁,但受限于宏观结构行为约束[8]。Whitcomb等[9]在研究织物性能时,提出了周期性边界理论。沿用该理论,张洁皓等[10]对复合材料编织板进行了多尺度性能研究。20世纪70年代,Bensousson等[11]提出了均匀化方法,该方法可将非均匀材料用一种等效的均匀材料来代替[12],马晓龙等[13]采用均匀化方法对平纹机织复合材料进行等效处理,并将均匀化模型损伤过程与试验结果对比,验证了该方法在机织材料仿真分析中的可靠性。
为此,本文以ABAQUS有限元软件作为分析平台,将周期性边界条件应用于多孔格栅周期性单胞,从单胞尺度建立格栅均匀化模型。通过不同模型的平压仿真结果,来分析该均匀化模型在格栅准静态力学性能仿真分析中的精度和效率。
2 多孔格栅周期性边界条件
2.1 三维周期性边界条件建立
本文研究的格栅结构是一种通过3D打印得到的新型三维周期性多孔格栅结构,该结构可作为夹芯层应用于轻型构件中。其沿坐标轴方向对称,格栅单胞面心处均有一方形通孔,图1展示了该格栅结构形态。M,N和K是沿坐标轴方向的单胞数量。周期性单胞长度为l,格栅单胞各分段长度为a和b,各方向壁厚均为t,材料是激光熔融的316L不锈钢。

图1 格栅形态及周期性单胞参数
首先对格栅单胞建立周期性边界约束。为满足三维格栅边界条件的建立,本文将编织板二维周期性边界条件[14]进行了拓展,探究了一种通用型的三维周期性格栅单胞边界约束方法。
本文围绕格栅单胞边界上的点、线和面分别建立节点型约束。首先将单胞外围虚拟出一个六面体外框,在外框顶部建立8个参考点A,B,C,D,E,F,G和H来虚拟单胞顶点位置。然后再对12条棱内的单胞节点和6个面所对应的单胞节点建立节点集L1~L12和F1~F6。其中L1~L4是与y轴平行的四条棱内节点,L5~L8是上表面四条棱内节点,L9~L12是下表面四条棱内节点;F1是单胞上表面不包含棱的面内节点,F2是单胞下表面不包含棱的面内节点,F3~F6是单胞侧面不包含棱的面内节点。

图2 单胞六面体外框各参数
格栅六面体外框的8个顶点不在图2所示周期性单胞上,所以对于复合材料编织板常采用的顶点约束方式不适用该类型单胞。本文采用面约束的方式,其约束方程可表示为
(1)
式中λ,ξ和ν分别为坐标系x,y和z三个方向的位移,下标为对应的面。
以式(1)的面F5,F2和F3作为主面,棱L4,L11和L12作为主棱,参考点A,C,D和H作为主顶点。单胞的其他边界面内节点和棱内节点以此为基础进行三维周期边界约束方程的建立。
面内节点的约束方程为
WF 1-WF 2-WH=0
(2)
WF 4-WF 3-WH=0
(3)
WF 6-WF 5-WC=0
(4)
式中W为节点位移,下标是对应的面内节点和主顶点。
式(2~4)建立了单胞六个外表面节点之间的约束关系,该约束方程保证了单胞相对边界面内节点运动的一致性。由于需保证节点位移沿坐标轴三个方向上均一致,所以W=λ,ξ,ν。
对于一个六面体来说,棱是两个面的交集。如果将12条棱包含在6个面内一起建立约束,就会产生过约束。所以需要将单胞外围12条棱单独建立约束。其棱内节点约束方程为式(5~13)。
对于棱L1,L3,L7,L8,L9和L10内节点,只需一个主顶点与其对应建立节点位移约束方程,就可实现其棱内节点约束。
WL 1-WL 4-WA=0
(5)
WL 9-WL 11-WA=0
(6)
WL 10-WL 12-WC=0
(7)
WL 3-WL 4-WC=0
(8)
WL 8-WL 12-WH=0
(9)
WL 7-WL 11-WH=0
(10)
棱L2,L5和L6与主棱不相邻,分别与主棱L4,L11和L12沿对角线共面,需两个主顶点位移约束才能使方程位移差为0。
WL 2-WL 4-WA-WC=0
(11)
WL 5-WL 11-WA-WH=0
(12)
WL 6-WL 12-WH-WC=0
(13)
参考点之间约束关系可表示为
WB-WA-WC=0
(14)
WG-WC-WH=0
(15)
WE-WH-WA=0
(16)
WF-WH-WA-WC=0
(17)
将式(2~17)通过编程输入ABAQUS中,可建立任意三维对称模型的周期性边界条件。
2.2 三维周期边界条件可靠性验证
对格栅单胞做准静态平压分析,并与文献实验结果[15]对比来验证所建立的周期性边界条件是否可靠。在面F4内任一节点处施加集中力Fz来求z方向位移变化量ΔL,通过式(18)进行名义应力和名义应变数值转换。
(18)
式中SA B F E是指参考点ABFE围成的面积,LD A是DA之间的距离。


图3 三类单胞的应力应变曲线

表1 三类单胞平压数据对比
3 均匀化模型建立及验证
3.1 弹性阶段数值分析
本文将格栅单胞的等效力学性能分为弹性和塑性两部分研究,均匀化模型的建立过程围绕这两个阶段进行。其弹性阶段的工程弹性常数可用格栅柔度矩阵(19)表示。
(19)
式中E为弹性模量,μ为泊松比,G为剪切模量。1,2和3对应x,y和z轴的方向。该格栅单胞是各向同性结构,其沿坐标轴各方向的等效弹性模量、泊松比和剪切模量数值相等。对单胞y方向进行剪切分析,对z方向进行平压分析,施加载荷均为20 N,其结果如图4所示。

图4 周期性边界条件下的单胞准静态位移云图
利用变形量和施加载荷之间的关系[14]可得到格栅α的等效弹性参数。采用同样的方法分析格栅单胞β和γ,三个模型的等效弹性参数列入表2。

表2 三类格栅等效弹性参数
3.2 塑性阶段数值分析及结果验证
塑性阶段应力应变数值通过式(20)求得。将图3应力应变数据代入,可得到均匀化模型塑性阶段应力应变值。
(20)
式中σm为塑性阶段应力值,σn为弹性阶段应力值,σt为模型总应力值。
将等效弹性参数输入ABAQUS建立的六面体均匀化模型的弹性栏,将塑性参数以样本点的形式输入塑性栏。再将格栅密度通过式(21)做等效处理。即为本文求得的均匀化模型。
(21)
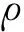
采用式(1~17)对均匀化模型建立周期性边界约束,并对均匀化模型平压,可得到图5所示的力位移曲线。对比格栅单胞模型和单胞层面的均匀化模型的平压仿真结果,两种分析方法的曲线近乎重叠,表明该方法在单胞尺度具有良好的准确性。

图5 格栅单胞与均匀化模型力位移曲线
4 均匀化模型平压性能分析
均匀化模型的建立过程是从格栅单胞出发,然后由单胞尺度向宏观层面延伸。这一过程会有误差产生。为避免模型误差对后文结论造成影响,首先对宏观层面的格栅均匀化模型精确度进行判定。
选用格栅β作为精细模型,单胞数M*N*K设定为3*5*3。将均匀化模型在尺寸上拓展,保证与精细模型外轮廓尺寸一致。采用准静态平压对两类模型均匀下压10 mm,将平压过程中压板对模型的作用力和模型变形量通过式(18)转换成名义应力和名义应变,可得到图6所示曲线。对比发现,两种模型的名义应力和名义应变曲线表现出一致性,两类模型最大误差不到2.8%。说明本文所建的均匀化模型精确度较高,不会因模型初始误差对后文推导出的结论产生较大影响。

图6 均匀化模型和精细模型应力对比
同条件下对两类格栅模型下压10 mm,得到图7所示的精细模型和均匀化模型Mises应力云图。由于格栅均匀化模型的结构和材料属性在均匀化处理之后均发生了改变,所以图示均匀化模型反映的应力情况和精细模型所展示的实际内部应力情况不符。说明本文所建的均匀化模型不适用于研究模型内部应力情况。
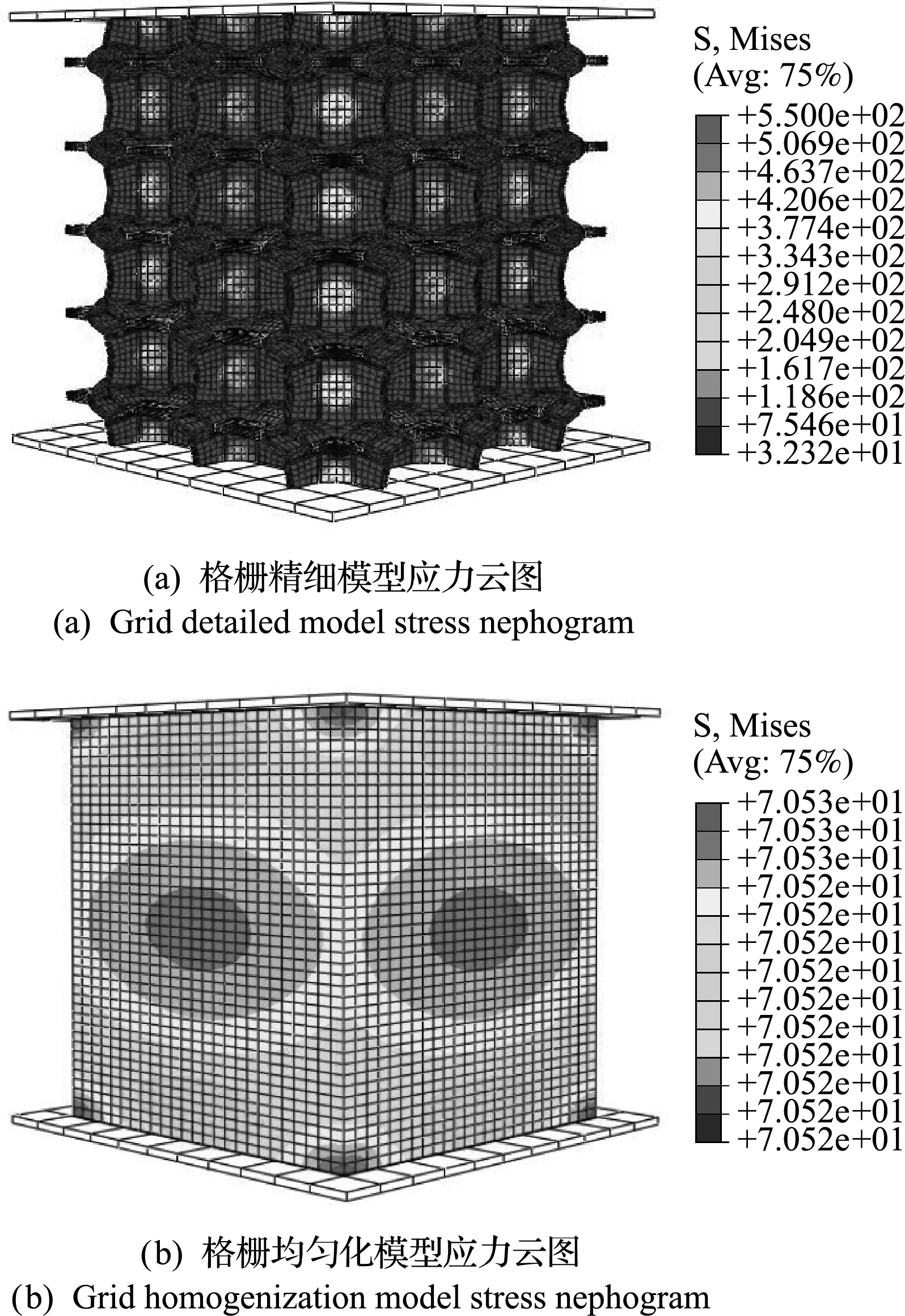
图7 精细模型与均匀化模型应力结果对比
本文着重对比分析不同格栅层数下精细模型和均匀化模型的外部受力和整体吸能情况。同样选用格栅β进行准静态平压分析,单胞数M*K设为定值3*3,格栅层数N分别设为1层、3层、5层和7层,平压位移和层数对应,分别为1 mm,3 mm,5 mm和7 mm。记录模型受力情况和开始分析到分析结束所消耗的时间。
格栅精细模型和均匀化模型平压受力情况如图8所示,两种模型在3*1*3芯层时的平压分析误差为24.8%,说明该均匀化模型处理1层格栅芯层时效果偏差。到3*3*3时误差迅速降低至3.1%,层数继续增加,两种分析方法计算结果趋于一致。这说明均匀化模型对多层级格栅,尤其是芯层达到5层以后的格栅结构,整体受力分析时的效果很理想。

图8 均匀化模型和精细模型平压受力对比
模型分析时间如图9所示。随着格栅层数不断增加,模型分析时间也不断递增。M*N*K从 3*1*3到3*7*3,精细模型分析时间分别是均匀化模型的0.67倍,2.5倍,4.29倍和5.37倍,并且这种趋势在扩大。这表明格栅层数越多,均匀化模型比精细模型处理得越快,相比精细模型,均匀化模型计算优势会随芯层数增加而越发明显。

图9 均匀化模型和精细模型平压分析时间对比
均匀化模型和精细模型的吸能情况列入表3。表中,S表示平压位移,Dm表示格栅精细模型吸能值,Hm表示格栅均匀化模型吸能值。格栅选用3*3*3,3*5*3和3*7*3三种类别,均从 1 mm 平压到7 mm,对比不同芯层和不同平压位移下的吸能值,发现均匀化模型吸能值和精细模型吸能值最大误差均未超过6%。说明本文建立的均匀化模型可很好地代替精细模型进行吸能性能分析。

表3 精细模型和均匀化模型吸能对比Tab.3 Comparison of energy absorption between detailed model and homogenization model
5 结 论
本文针对多孔格栅结构,开展了格栅周期性边界条件与均匀化模型的研究工作。通过有限元方法,对周期性边界条件下的格栅单胞弹塑性性能进行仿真分析,建立了具有等效弹塑性性能的格栅均匀化模型。将格栅均匀化模型与精细模型平压性能对比,得出以下结论。
(1) 格栅层数增加,精细模型的计算时间随之成倍增加,而均匀化模型的计算成本低,所以不会随格栅层数增加而消耗大量计算时间。且层数越多,均匀化模型相比精细模型的计算速率越高。
(2) 格栅均匀化模型可替代精细模型进行平压整体受力和吸能分析。
(3) 均匀化方法可作为周期性结构仿真分析时节省计算量而采取的一种手段。

