滑坡冲击铲刮变量的计算方法研究
高 杨, 高浩源, 李 滨,, 赵志男
(1.中国地质科学院 地质力学研究所 新构造运动与地质灾害重点实验室,北京 100081;2.长安大学 地质工程与测绘学院,西安 710054)
1 引 言
高速远程滑坡的冲击铲刮效应是指滑坡从高位山体失稳剪出后凌空加速坠落运动过程中,滑坡在较大的势动能转换时运动速度大幅度增加,形成了巨大的冲击动能并铲刮下部地表岩土体,导致滑体体积放大。该类滑坡通常剪出口和地面高差大于100 m,最大运动速度达到20 m/s以上[1-3]。高速滑坡动力学作用过程中,滑体同周围山体发生动力接触,导致次级滑坡发生或侵蚀其他岩土体,使滑坡体积成倍增加至初始滑体体积的1~4倍[4-7],形成灾害连锁反应,灾害规模和成灾范围放大明显,导致群死群伤灾害事件发生。
近些年来,国内外许多研究者对滑坡灾害的动力侵蚀相关领域开展了研究,为揭示滑坡铲刮机理提供了指导[8-14],但关于铲刮理论的计算方法仍存在以下三点问题。
(1) 基于铲刮率计算方法。目前大量的研究成果聚焦于泥石流运动过程中的侵蚀裹挟效应,大多数是基于侵蚀率和铲刮范围进行评估,采用浅水方程计算得出铲刮体积,主要是根据经验分析和数学方法得出铲刮变量(铲刮体积、铲刮范围和铲刮深度)。
铲刮率计算分为四步。
① 根据滑前体积V0、滑后体积Vf和铲刮路径长度S,给出经验铲刮率Es为
Es=ln(Vf/V0)/S
(1)
② 根据铲刮率Es、滑体厚度h和运动速度v,计算滑体对运动路径基底的铲刮速率Et为
Et=Eshv
(2)
③ 将铲刮速率Et代入流体动量方程(x方向)计算铲刮体积为
(3)
式中ρ为滑体密度,h为滑体厚度,t为时间,gx为重力加速度在x方向上的分量,σz为z方向上的正应力,vx为x方向上的速度,b为基底铲刮深度,kx=σx/σz,τz x为基底剪应力。
④ 根据增加的铲刮体积和铲刮区面积对铲刮深度进行求解。
该计算方法中铲刮率和铲刮范围的确定大多依靠地质工作者的野外实地调查经验,虽然该方法具有计算效率高的实用价值,但也存在力学分析较弱和评估精度较差等问题。
(2) 基于冲击屈服计算。基于力学机理的冲击铲刮效应研究大多集中于撞击力和屈服破坏准则之间的临界作用关系[15,16]。撞击力的计算多以Hertz接触力学为基础(式(4)),采用材料的弹塑性屈服理论(式(5)),给出了滚石撞击地面的临界屈服速度和屈服力(式(6))[14]。该研究方向为冲击铲刮定量化计算提供了很好的求解思路,但是只解决了滚石的正向碰撞屈服和临界速度vy的问题,对于滑坡铲刮全过程的主动冲击力、剪切力、被动屈服破坏范围和体积等铲刮变量的计算问题,仍需进一步深入研究。
(4)
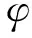
(5)
(6)

(3) 冲击铲刮分析模型。Iverson等[17,18]建立了经典三层式的铲刮二维模型,三层材料自上而下分为滑体层、铲刮层和基底层,从动量和质量交换的角度求解铲刮变量,但该分析模型采用滑体同铲刮层平行接触进行研究,未考虑滑体前缘或侧缘空间尺度的冲击情况,也未考虑不同几何尺度下边界力求解的问题。因此,滑坡冲击铲刮过程在不同接触几何形态下的计算方法需进一步完善。
综合目前研究存在的问题,本文在前人研究的基础上开展研究,求解过程分为以下四个步骤。(1) 基于Hertz准静态接触理论,进行撞击力求解; (2) 基于弹性力学应力传递,计算撞击力对受铲刮层产生的附加应力和总应力; (3) 选取适用的岩土体屈服破坏准则; (4) 对铲刮层的屈服破坏边界进行求解,对滑坡冲击过程中的最大铲刮深度和铲刮范围等铲刮变量进行定量化计算。研究结果对高位滑坡动力学研究与风险预测评估工作具有重要意义。
2 冲击铲刮地质力学模型
滑坡失稳后经历了高位剪出-凌空飞行-冲击铲刮-碎屑堆积四个运动阶段,往往会形成高速远程滑坡灾害,影响范围广,对人类的生产生活带来极大的威胁。
(1) 高位剪出阶段。高位远程滑坡往往发育在地形地貌陡峻、岩体结构面切割强烈和地层岩性为硬岩的山体,滑坡剪出口和地面高差大于100 m,滑前灾害调查难度较大,一旦失稳会对周围人类生命财产造成毁灭性的伤害。
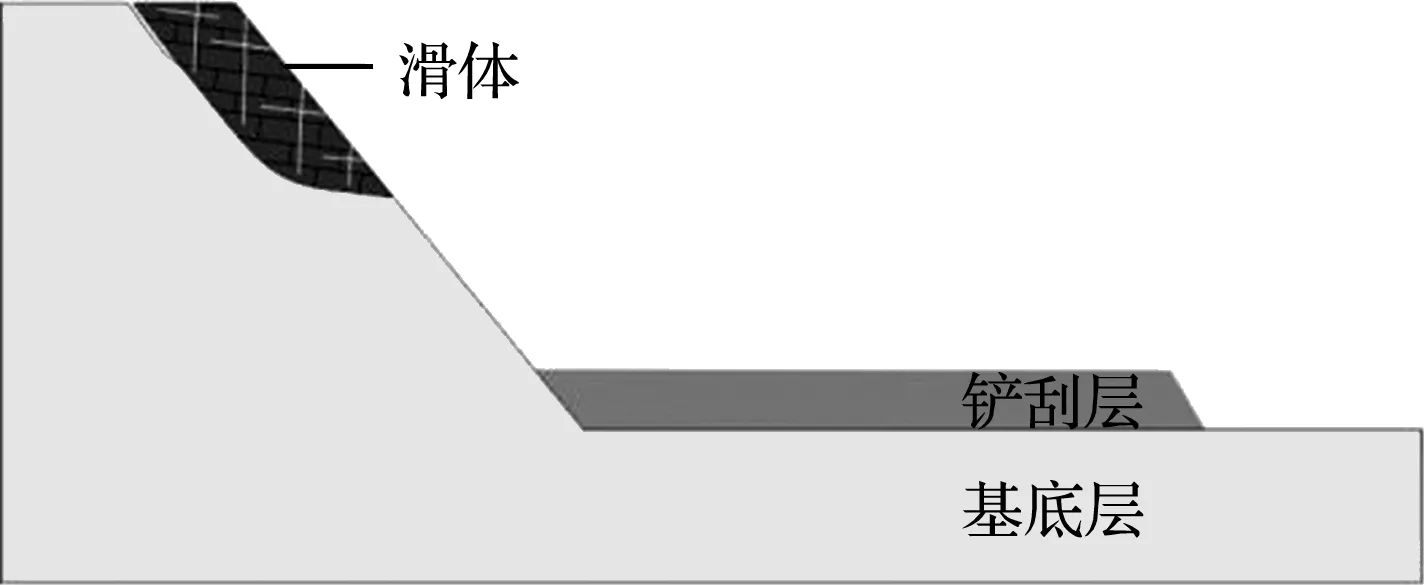
图1 滑坡运动过程高位剪出阶段
(2) 凌空飞行阶段。较大的地形落差为滑体提供了较好的势动能转换空间,使滑体具有巨大的冲击动能和运动速度,最大速度通常可以超过20 m/s。在运动过程中,由于结构面的存在和运动速度的差异性分布,滑体逐渐解体散开,并带着巨大动能进入铲刮区,冲击铲刮周围岩土体。
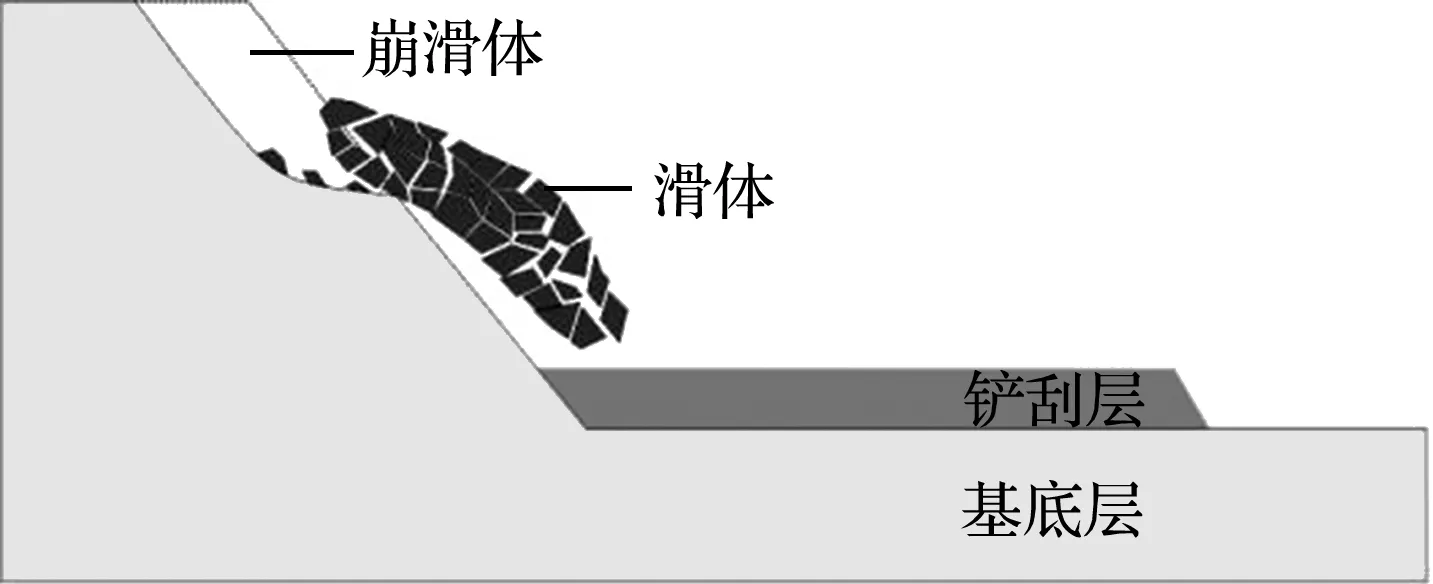
图2 滑坡运动过程凌空加速阶段
(3) 冲击铲刮阶段。滑体前缘以较高的速度冲击铲刮层,导致铲刮层材料屈服破坏,铲起后经过能量传递获取一定的动能,并汇入滑体一起运动,使滑体体积明显增加,并容易在边界层形成一层颗粒滚动摩擦带,使滑坡运动距离和成灾范围有所增加,直至滑体动能无法导致铲刮层破坏,铲刮作用即消失,滑坡运动进入碎屑堆积阶段。
图3 滑坡运动过程冲击铲刮阶段
(4) 碎屑堆积阶段。滑体经过铲刮阶段后,滑体不断解体,颗粒粒径进一步减小,且磨圆度相对增加,堆积体基本呈现坡脚为大块体,前缘为小块体,上层为大块体,下层为小块体的堆积形态。在摩擦阻力作用下,滑体动能逐渐消耗殆尽,滑坡停止运动。
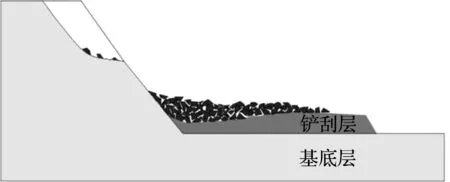
图4 滑坡运动过程碎屑堆积阶段
3 冲击铲刮计算方法
根据高速远程滑坡运动过程的定性分析,对滑体冲击铲刮的力学作用过程进行定量计算。
3.1 基本假定
(1) 在分析中采用准静态方式进行计算,系统的作用时间T与作用于系统的力脉冲周期2t*相比很短,碰撞中接触力的变化主要按照准静态方式来进行分析[16]。
(2) 假设撞击体为不转动的均匀质量球体,不考虑Hertz接触导致土体的塑性屈服,仅考虑接触力的计算。
(3) 假设铲刮层为理想弹塑性体,且不考虑瞬时加载导致的土强度增加。
(4) 假设在笛卡尔直角坐标系XOZ进行计算分析,接触点为坐标原点。
(5) 假设土层原有自重应力场的侧向土压力系数为K0=1,具有静水压力性质,不改变附加应力场的主应力大小和方向。
(6) 采用二维分析方法分析,假设在y方向存在无限长的均布荷载,认为荷载长度≥5B(B为所受荷载宽度)时,应力分布与无限长时分布相差较小,则可用每延米的平面应变状态求解。
3.2 冲击力计算
高位滑坡的滑体运动过程往往具有一定的凌空飞行阶段,经历了较大的势动能转换空间。滑体斜向冲击铲刮层,冲击力可以分为竖向冲击力和切向冲击力,采用Hertz弹性接触理论计算竖向力,采用基底摩擦阻力理论计算切向力。具体理论公式如下。
(1) 竖向冲击荷载
接触压力与接触深度的关系为
(7)


图5 Hertz接触理论的概化模型
接触压应力与接触半径之间的关系为
(8)
式中a为最大接触半径;r为接触半径变量,取值为0~a;P(r)为随半径变量的压应力,当r=0时为最大压应力。
接触半径与接触深度之间的关系为
a2=Rδn
(9)
(10)

最大竖向接触力为
(11)
(2) 切向剪切荷载
对于基底阻力模型,根据竖向荷载得到基底切向阻力,切向阻力模型为同摩擦系数相关的牛顿摩擦模型。计算中需用到正压力数值,正压力值由Hertz力或者滑体自重提供,当存在竖向速度时由Hertz力提供;当竖向速度为0时,正压力值由滑体自重提供。

(12)
式中Pt为正应力,μ为摩擦系数,Pn为切应力。
3.3 屈服准则选取
下垫层受铲刮破坏主要体现在岩土体的物理力学性质上,受铲刮材料的应力状态和屈服准则成为了判断下垫层屈服的关键条件。高位滑坡冲击铲刮作用大多是在地表,不存在高围压条件,可以选取较为常用的抗剪强度q与平均应力p之间为直线关系的屈服准则,通常可以选用莫尔-库仑强度准则(MC准则)和广义Mises准则(DP准则)。莫尔-库仑强度准则是描述剪切面上剪应力τ与该面上正应力σ间关系,表明岩土材料引起材料破坏不是由于最大剪应力,而是由于某个平面上τ-σ的最危险组合;广义Mises准则在应力空间的曲面和在π平面上的轨迹都是光滑的,因而作为屈服准则进行数值计算是比较方便的[19]。本文解析选用经典MC屈服准则进行分析,可表示为
τ=c+σtanφ
(13)
式中c为粘聚力,φ为内摩擦角。
用主应力可以表示为
sinφ=(σ1-σ3)/(σ1+σ3+2ccotφ)
(14)
式中σ1和σ3分别为大小主应力,c为粘聚力,φ为内摩擦角。
3.4 点荷载塑性边界计算
理论解析在二维的XOZ直角坐标系平面内进行,由于线荷载沿y方向均匀分布且无限延伸,因此与y轴垂直的任何平面上的应力状态都完全相同,属于弹性力学的平面应变问题,只需求解σz,σx和τx z三个量。
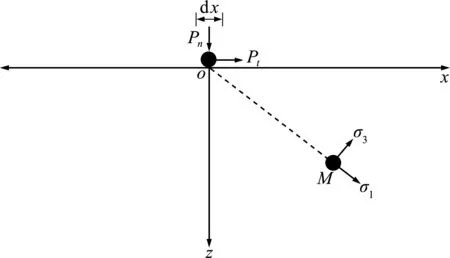
图6 附加荷载对点M处的附加应力概化
基本的计算思路是根据地表撞击荷载应力P(竖向和切向)求得铲刮层半无限空间中任意点M处的附加应力状态[20],进而求得该点处的主应力,再根据莫尔库仑屈服准则作为塑性临界范围的判定条件,将大小主应力代入到极限平衡条件,得出塑性区的轨迹方程。
(1) 某点M的附加应力状态求解
① 竖向荷载导致点M的应力状态,根据弹性力学Boussinesq解,求得点M附加应力状态如下,
(15)
(16)
(17)
② 切向荷载导致点M的应力状态,根据弹性力学Cerruti解,求得点M切向附加应力状态如下,
(18)
(19)
(20)
竖向和切向共同导致点M的总附加应力状态为
σz=σz,n+σz,t
(21)
σx=σx,n+σx,t
(22)
τx z=τx z,n+τx z,t
(23)
(2) 某点M的大小主应力计算
附加荷载导致铲刮层中某点M的附加主应力为
(24)
(25)
假设土层原有自重应力场的侧向土压力系数为K0=1,具有静水压力性质,不改变附加应力场的大小主应力大小和方向,则点M大小主应力计算公式为
(26,27)
式中γ为土的重度,z为点M的深度。
根据求得大小主应力σ1和σ3,代入到MC极限平衡条件求解(式(14)),得到塑性区的轨迹方程,并根据竖向和切向荷载的大小关系,塑性滑移线可以分为表层滑动面和深层滑动面,即竖向冲击为主的铲刮为深层滑移线,切向裹挟为主的铲刮为浅层滑移线。
塑性区边界方程为

(28)
4 实例计算
由于公式较为复杂,在计算过程中采用Matlab解方程编程软件进行计算和成图,公式求解共分为两个部分。第一部分为撞击力求解,首先定义公式的变量参数(如质量m和速度v等),然后根据实际案例给参数赋值,将定义的参数编制撞击力计算公式;第二部分为破坏区求解,首先定义公式的变量参数(粘聚力c、内摩擦角φ和重度γ等),然后根据实际案例给参数赋值,将定义参数根破坏区边界方程编制公式,最后将第一部分撞击力计算公式代入求解成图。以下主要分为仅竖向加载及竖向和切向共同加载两种计算工况进行分析,具体计算参数和铲刮层塑性区边界轨迹线结果如下。
4.1 材料参数
铲刮层材料为第四纪残坡积土,其粘聚力为15 kPa,内摩擦角为25°,泊松比为0.32,弹性模量为24 MPa,密度为1.8 g/cm3;撞击块石为灰岩,直径为0.5 m,弹性模量为4×104MPa,泊松比为0.2,半径为0.5 m,质量为1400 kg。
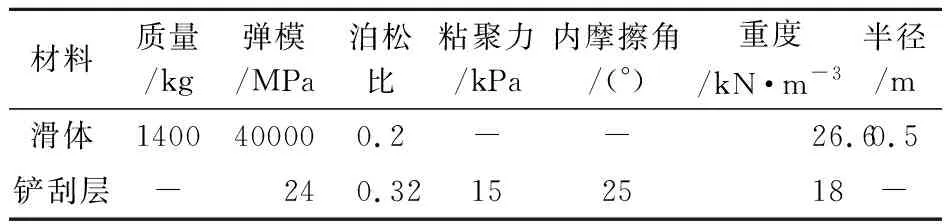
表1 灰岩滑体冲击地面的计算参数
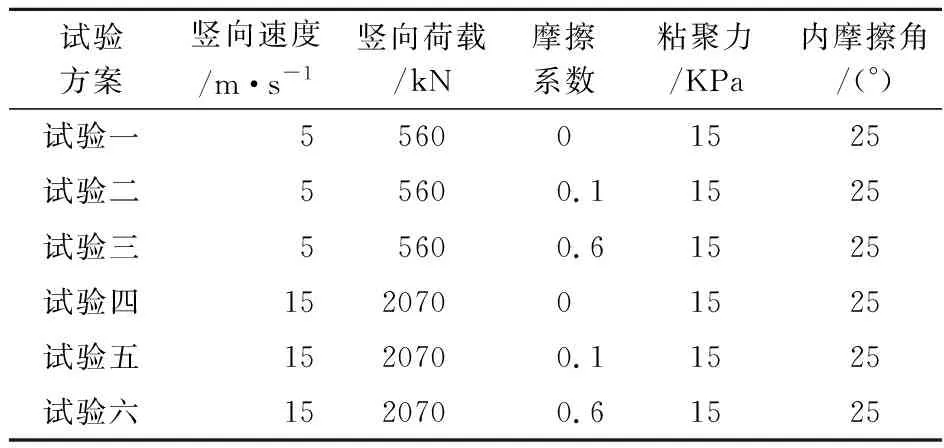
表2 可铲刮层塑性区计算参数
4.2 计算结果
根据竖向速度,可以计算出瞬时Hertz接触力,切向牛顿摩擦模型主要取决于正应力与摩擦系数,与水平速度分量无关。为体现高位远程滑坡运动过程具有的明显冲击铲刮特性和对比特征,滑体的竖向冲击速度分别取5 m/s和15 m/s,切向摩擦系数分别取0(仅竖向冲击),0.1和0.6。通过公式编程可得x对z的方程轨迹线,即塑性区边界线。同附加荷载导致的可铲刮层塑性区边界范围如图7所示。在不考虑切向荷载时,铲刮层塑性区主要以竖向发展为主;在考虑切向荷载时,铲刮层塑性区沿切向力方向迁移,当切向力足够大时,塑性边界贯通至地面。计算结果体现了滑体冲击铲刮作用后地面塑性区的几何形态。

图7 施加附加点荷载后可铲刮层塑性区边界轨迹
5 动力学解析方法
以上介绍了滑体同铲刮层动力接触边界层中,某点某一时刻的冲击荷载的解析计算方法,关于整体和动态求解做以下讨论。
5.1 整体求解
针对整个滑体对铲刮层塑性区的求解,同理点荷载的附加应力的求解,考虑滑体同铲刮层边界的多点接触,对铲刮层中某一点的附加应力状态和大小主应力求和,进而算得铲刮层的塑性区边界轨迹线,但是由于计算公式较为复杂,需要借助计算机编程来方便计算。
受到P1,P2…Pi…Pm荷载作用,作用点横坐标分别为x1,x2…xi…xm。
第i个竖向荷载引起M附加应力状态为
(29)
(30)
(31)
第i个切向荷载引起M附加应力状态为
(32)
(33)
(34)
则第i个荷载在点M处引起的附加应力状态大小为
(σz)i=(σz ,n)i+(σz ,t)i
(35)
(σx)i=(σx ,n)i+(σx ,t)i
(36)
(τx z)i=(τx z ,n)i+(τx z ,t)i
(37)
则P1,P2…Pi…Pm所有荷载在点M引起的附加应力状态大小为
(38,39)
(40)
重复式(24~27)求得点M的主应力,在代入屈服准则中对临界深度z的轨迹线进行求解,得到塑性边界轨迹。
5.2 动态求解
动态求解大多运用在数值模拟计算中,数值模拟方法也是将算法有效实现的一种方法,解决了算法迭代带来的计算困难问题[21,22]。在滑坡运动过程中,在求得某一时刻的滑体整体轨迹线的同时,需要增加时间尺度,计算过程采用滑体运动数据和铲刮层塑性轨迹线数据耦合互馈计算的方法。前期滑坡动力学研究中,研究视角往往是聚焦在滑体运动,但是在滑坡的冲击铲刮研究中还需要增加铲刮塑性区计算的视角,也就是说在某一时步计算完滑坡的运动状态后,需要记录接触边界上滑体对铲刮附加荷载的接触力数据,进而求得该时步情况下,铲刮层塑性区的分布情况,接触边界为上一时步的塑性区边界。随后根据实际的作用力进行不断的迭代计算,直至作用力不足以引起铲刮层的屈服破坏。
具体理论计算过程步骤如下(图8)。
(1) 初始计算参数赋值。给出滑坡运动的初始参数(包括滑体材料参数和运动边界条件等)。
(2) 获取滑体运动参数。根据运动方程,计算滑体运动的运动学参数(滑体厚度和滑体运动速度等数据),时刻设为ti。
(3) 继续或停止运动判别。若此时刻滑体内的最大运动速度vmax=0,则计算结束;若最大运动速度vmax>0,则进入步骤(4)。
(4) 搜索边界力。根据滑体运动参数计算滑体与运动路径之间的边界力。
(5) 应力求解。根据边界力计算铲刮层某一点处的附加应力和总应力。
(6) 屈服破坏准则判别。根据屈服破坏准则,判别边界力作用下,铲刮层表层是否达到破坏条件。若未发生破坏,则进入步骤(9);若发生破坏,则到步骤(10)。
(7) 铲刮变量计算。根据附加应力和总应力,计算ti时刻的铲刮变量(破坏区深度、破坏区范围和破坏区体积等)。
(8) 受破坏材料汇入滑体。破坏区材料汇入滑体中,接收滑体的能量传递获取动能后,随滑体一起继续运动。
(9) 下一时刻循环计算。开始新一轮ti + 1时刻的滑体运动参数和铲刮变量的计算,直至滑体动能减小至无法引起底部的铲刮破坏,最终经过步骤(3)判别,运动停止。
(10) 计算结果。得到滑体运动堆积结果(运动速度和堆积厚度等)和铲刮屈服破坏结果(铲刮区几何形态和铲刮体积等)。

图8 计算流程
6 结 论
高位滑坡的冲击铲刮效应往往导致滑坡体积成倍放大,增加了灾害的成灾规模和危害性。本文采用力学理论解析方法,解析了高位滑坡冲击荷载下铲刮层塑性区域的计算过程。
(1) 采用Hertz接触力学、岩土力学和弹性力学附加应力求解理论,推导了铲刮层中某一点处附加竖向和切向荷载导致附加应力状态求解过程,并根据主应力和塑性区判识准则确定了铲刮层塑性边界轨迹线。
(2) 结合实际岩土体材料计算了冲击荷载下,铲刮层的塑性边界轨迹线,可以看出,在不考虑切向荷载时,塑性区主要以竖向发展为主;在考虑切向荷载时,铲刮层塑性区具有沿切向方向迁移的趋势,直至塑性边界贯通至地面,以此可以对铲刮层的铲刮变量进行计算。
(3) 基于点荷载铲刮层塑性区的理论解析,对滑体整体和运动过程中动态求解进行了相关讨论,为进一步分析高速滑坡动力学过程提供了计算思路。
——以牛儿湾滑坡为例

