基于应变模态和稀疏贝叶斯学习的网架结构损伤识别

仇树茂， 杨海峰， 吴子燕， 李梦莹， 悦 峰

(西北工业大学 力学与土木建筑学院，西安 710129)

1 引 言

随着服役周期的增长，工程结构必然会有结构性能和功能的退化，并且大多表现在局部区域[1,2]。结构的模态参数是其固有属性，而损伤就意味着模态参数的改变。相较于频率和位移模态，应变模态对局部损伤更加敏感[3]，具有更好的损伤识别能力。Cui等[4]利用从实际结构中获取的应变模态构建了三种指标，识别出梁式结构的裂纹和腐蚀损伤位置。Zhao等[5]采用损伤前后的应变模态差对桥梁结构进行损伤识别，并结合统计趋势分析和置信概率来提高方法的鲁棒性。上述方法充分发挥了应变模态计算简单且损伤定位能力强的特点，但是构造的损伤检测指标不含任何结构性意义，难以定量计算损伤程度。

通过用表征结构单元损伤程度的损伤系数对刚度矩阵进行折减，结合相关模态参数，可以对损伤程度进行定量分析[6-9]。在实际应用中，模态数据的测量受到环境和传感器布置等因素的影响，存在很多不确定因素，可以采用贝叶斯方法来准确和恰当地量化参数的不确定性[10,11]。结构损伤识别的稀疏贝叶斯学习方法主要思路是，首先将单元刚度损伤系数作为目标参数，利用结构损伤通常具有空间分布稀疏性的特点，建立多层次稀疏贝叶斯学习模型。通过贝叶斯网络建立实测数据和损伤系数之间的关系，利用贝叶斯推理方法求解损伤系数关于实测数据的后验概率密度分布，最后利用迭代优化算法估算出最大后验概率(Maximum a posteriori)密度处的损伤系数值，从而实现单元级别的损伤定量识别。Huang等[1]将其应用于含有16个子结构的钢支撑框架结构，取得了满意的效果。崔健[12]将该方法应用于含有24个单元的6层框架结构，并利用吉布斯采样的方法提高了算法的鲁棒性。

由于稀疏贝叶斯学习算法需要对结构每个单元进行迭代计算，对于大型复杂结构而言，存在计算时间长、效率低和对振型完备性要求高等问题，现有研究也主要针对结构单元较少或者简化模型的情况。本文针对一个128杆的空间网架结构，首先利用单元应变模态差进行初步损伤定位，找出疑似损伤单元，只对这些单元进行稀疏贝叶斯学习迭代计算。在发挥应变模态计算简单和损伤定位能力强等特点的同时，仅利用一个方向的振型信息成功识别出了损伤的位置以及程度。本文所提损伤定位及损伤程度识别两步法的流程如图1所示。

图1 损伤定位及损伤程度识别两步法流程

2 基于单元应变模态差的损伤定位

应变模态能反映结构的固有特征，且对损伤较为敏感，利用结构损伤前后单元应变模态的差值，便可以判断损伤位置。为了方便比较，将单元应变模态差按最大值归一化，定义单元应变模态差指标，

(1)

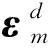
3 含损伤系数的有限元模型及贝叶斯网络构建

对于拥有n个单元，d个自由度的目标结构，其具有已知质量矩阵M和基于子结构单元刚度矩阵线性组合的整体刚度矩阵K。使用低振幅振动进行结构的模态识别，采用经典的线性动力学模型，则无需对阻尼矩阵进行建模。

假设质量矩阵M在损伤前后不发生改变，主要考虑结构的刚度损伤，使用刚度损伤系数θ=[θ1,…,θn]来表征各单元的损伤程度。此时结构的整体刚度矩阵可以表示为

(2)

对于多自由度系统，在不考虑阻尼矩阵时，特征方程为

(3)

式中i=1,…,m。通过特征方程可以建立刚度损伤系数与系统模态参数的关系。

特征方程是一种理想模型，实际问题中，存在不可避免的模型误差，该等式并不能完全满足。针对这种情况，对每一阶模态的特征方程右边加入一个误差变量ei(i=1,…,m)。定义该变量服从均值为0，方差为β-1的高斯分布，则式(3)可改写为

(4)

右端项ei∈d(i=1,…,m)。

图2 各参数的贝叶斯网络

4 贝叶斯推理模型

4.1 刚度损伤系数和模态参数的先验密度分布函数

由式(4)可得目标参数θ,ω2和φ基于β的联合先验概率密度分布函数为

p(ω2,φ,θ|β)=c0(2πβ-1)-d m /2exp

(5)

式中c0为归一化常数，m为实测模态阶数，d为模型自由度数。因为β：Gamma(a,b)，所以有

(6)

为了方便处理式(5)，引入矩阵H,F,b,c和G，可表示为

(7a)

(7b)

(7c)

(7d)

(7e)

此时，会有

‖Fφ‖2=‖Hθ-b‖2

(8)

将式(8)代入式(5)，并对参数θ积分，可得关于ω2和φ的边缘先验概率函数

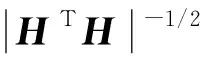
(9)

又由式p(θ|ω2,φ,β)=p(ω2,φ,θ|β)/p(ω2,φ|β)可得

(10)

4.2 系统模态参数的似然函数

(11)

(12)

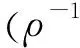
(i=1,…,m)(13)

(14)

这样，系统模态参数的似然函数可以写为

(15)

4.3 各参数的联合后验概率密度函数

将以上贝叶斯模型的各部分结合起来，由贝叶斯公式可以构造出以测量数据为条件的所有不确定参数的联合后验概率密度函数，如式(16)所示。其中p(τ)∝1，p(ν)∝1，故在此没有列出。

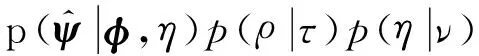
(16)

4.4 贝叶斯推理

(17)

(18)

(19)

(20)

(21)

(22)

(23)

θnew=(HTH)-1HTb

(24)

(25)

对于本文最关心的刚度损伤系数θ，其后验协方差由式(25)获得，当未对θ设置先验信息时，先验协方差矩阵A取为方差非常大的对角矩阵[1,11]。

(26)

在执行迭代步骤前，设置损伤单元的初始值θ0为1附近的随机数。最终各参数的MAP值按照式(18～25)的顺序不断迭代获得，当损伤系数θ前后两次迭代值之差的无穷范数足够小时(本文取10-3)，迭代终止。

5 算 例

5.1 空间网架模型

选取某空间网架结构验证本文所提方法的准确性。该结构的网架尺寸为2.12 m×2.12 m×0.33 m，下层三跨，上层四跨。具有40根上弦杆，24根下弦杆，64根腹杆，杆件为Φ10 mm×2 mm的空心杆，节点采用螺栓球节点。结构共计128根杆和41个节点。网架各部位均采用钢材制成，弹性模量206 GPa，密度7850 kg/m3，泊松比为0.3。网架上层四个角点处采用固定约束。

根据网架模型的设计方案加工构件，在实验室进行实体网架模型的组装。使用有限元软件ANSYS建立上述结构仿真模型，其中假定节点为铰接，采用Link180单元模拟杆件，Mass21单元模拟铰节点，该结构的总自由度数d=111。

将网架的每一根杆件视作一个单元。本文拟选取两种损伤工况，工况1为60号杆件发生100%损伤(θ60=0)；工况2为60号和68号杆件分别发生100%和50%损伤(θ60=0，θ68=0.5)。其中60号杆为下弦杆，68号杆为腹杆。网架结构实验模型、仿真模型以及定义损伤工况的杆件位置如图3所示。

图3 网架结构及损伤位置

5.2 结果和分析

实验测量了所有杆件的应变和所有节点竖直方向上的加速度数据，用实测数据对仿真模型进行了模型修正。在结构损伤阶段，用砂轮在杆件局部制造断口来模拟定量损伤，以截面切割程度大致刻画损伤程度，由于仅用于损伤位置的判断，所以无需深究切割的准确程度。根据前述方法用测量的应变数据构造应变模态差指标进行损伤位置的初判，结果如图4所示。

从图4可以看出，单损伤工况1时，在损伤单元60处，第一阶应变模态差指标明显高于未损伤单元；多损伤工况2时，在单元60处和68处，该指标同样高于未损伤单元。分别选取指标最大的前十个单元作为疑似损伤单元，其余单元则视为未损伤。对于工况1，选取31，50，59，60，61，63，74，108，115，124单元；对于工况2，选取31，57，59，60，61，63，68，92，95，127单元。

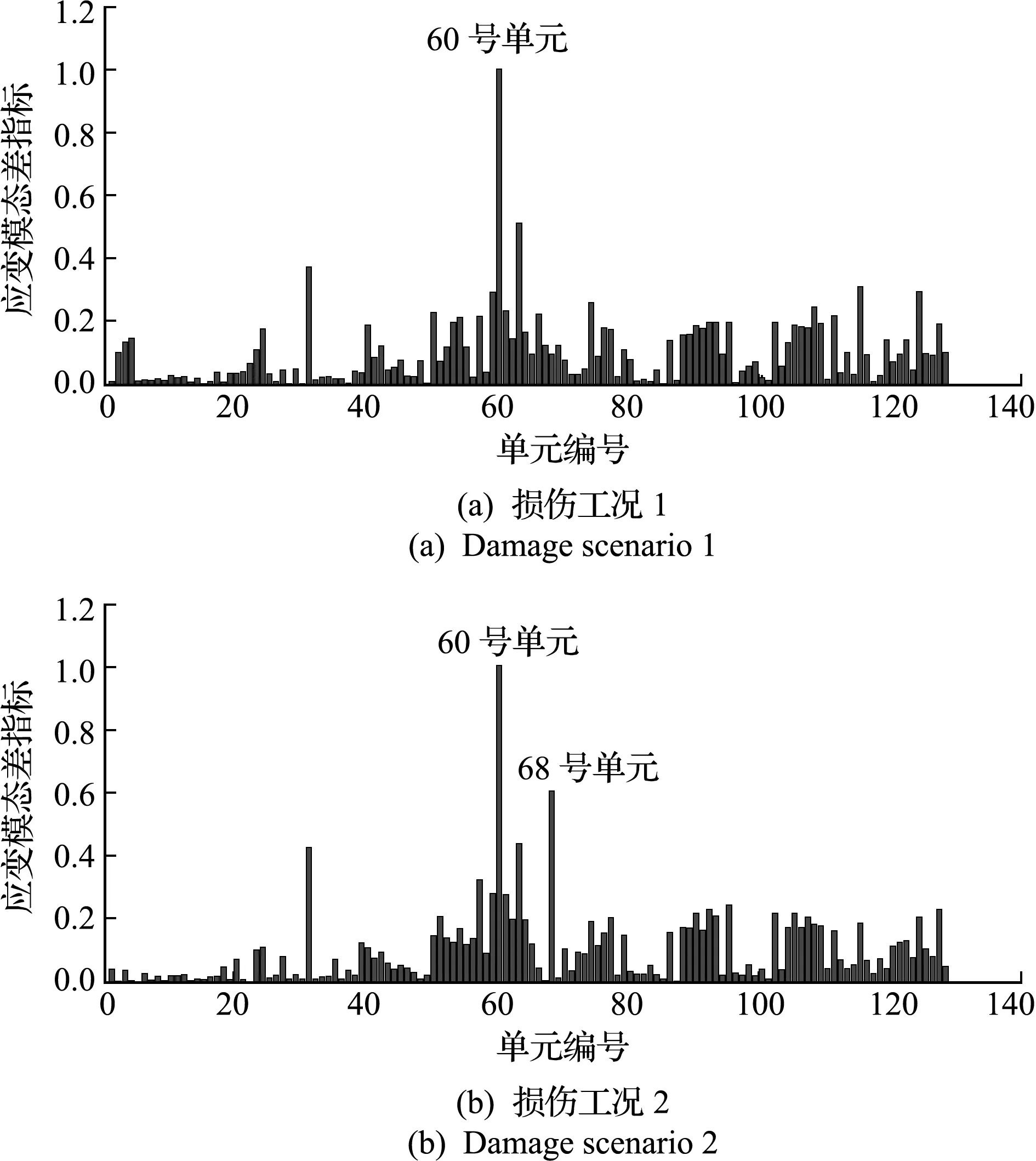
图4 不同工况下疑似杆件识别结果

为上述疑似杆件单元赋予刚度损伤系数，其余杆件对整体刚度矩阵的贡献记作K0。利用修正后的ANSYS有限元模型，以弹性模量的折减来反映单元损伤，提取损伤后前5阶竖直方向的质量归一化振型以及相应频率，利用稀疏贝叶斯学习算法在疑似杆件单元之间进行迭代计算，进一步判别损伤位置以及程度。为了模拟环境噪声的影响，为振型添加均值为0，标准差为振型测量值均方根3%的高斯噪声，以此来生成15组结构振动响应仿真数据。最终识别结果如图5和图6所示。

图5 工况1疑似杆件识别结果

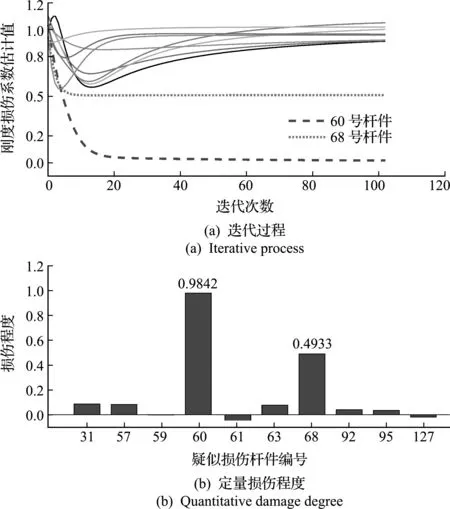
图6 工况2疑似杆件识别结果

对于损伤工况1，从图5可以看出，在60号杆件完全截断时，其刚度损伤系数从初始值逐渐趋向于0，其余疑似杆件趋于1附近，60号杆件损伤程度识别结果为98.62%，与实际较为符合。

对于损伤工况2，从图6可以看出，60号和68号杆件单元的刚度损伤系数分别收敛于0和0.5附近，其余疑似杆件收敛于1附近，60号和68号相应的损伤程度最终识别结果分别为98.42%和49.33%，其余杆件认为没有损伤。未损伤杆件的θ值最终收敛于1附近，有可能产生θ略大于1的情况，从而损伤程度1-θ的识别结果为负数，当损伤杆件的识别结果远大于其余杆件时，可以认为本文所提方法能有效识别损伤的位置以及程度。

如图7所示，若不事先对疑似损伤杆件进行预判，仅基于前五阶竖向振型及相应的频率值对每个单元计算，会使迭代次数显著增加，计算效率降低，出现大量损伤误判甚至是不收敛的情况，并不能有效识别损伤。在这种情况下，需要更多其他方向的振型测量数据，对于网架结构来说，在节点处布置多个方向的传感器并不是一件容易的事情，工程中难以实现。

图7 不同工况下所有杆件识别结果

由以上结果可知，无论是单损伤还是涉及网架不同杆件种类的多损伤，基于一阶应变模态差指标完成初步损伤定位，再者利用稀疏贝叶斯学习算法对疑似杆件进一步验证，可以精确识别结构的损伤位置以及程度。

6 结 论

针对传统稀疏贝叶斯学习算法在复杂结构损伤检测中存在的计算效率低和振型完备性要求高等问题，提出了损伤识别的两步法，首先利用损伤前后应变模态差初步判定损伤范围，然后利用稀疏贝叶斯学习算法，以单一方向振型值作为输入进行精确的损伤定位定量分析。以一个空间网架结构为对象，分别针对单位置损伤和多位置损伤进行了验证。结果表明，在振型测量数据量减少2/3的情况下仍能成功识别损伤的位置以及程度，所需总计算时间约为不采用两步法的1/12。本文研究结果为大型复杂结构损伤识别方法的实用化提供了一种新思路。

后续工作将探寻仅使用一次测量数据来完成损伤的定位以及精确识别的可行性。