基于坐标映射的类周期电磁金属阵列布局设计的灵敏度分析方法

王 奇， 袁 坷， 高仁璟， 刘书田

(大连理工大学 工业装备结构分析国家重点实验室，大连 116024)

1 引 言

类周期电磁金属阵列已成功应用于多种类型的电磁器件中，以实现其电磁辐射或散射性能的提升设计，如电磁超表面、反射板天线和光学透镜等[1-4]。类周期电磁金属阵列可描述为由多个相似形状的电磁金属单元按照特定的布局参数排列组成。布局参数通常包括各单元的尺寸、转角以及布置位置。对于类周期阵列，其布局参数往往规模较大且相互独立。根据特定的功能需求，如何设计和发现满足性能要求的类周期电磁金属阵列布局形式是关键。典型的例子是异质电磁超表面的设计问题，其基本思想是通过优化设计类周期电磁金属阵列的布局形式，使其等效阻抗特性随空间位置合理变化，进而实现表面波抑制、场传输或电磁辐射性能的进一步提升[5]。与周期性电磁金属阵列相比，类周期阵列不再局限于周期性布局形式的限制，设计自由度大幅增加，但也导致用以描述类周期阵列布局形式的参数规模更大，优化设计问题的求解更为复杂。

利用进化类算法可以优化类周期电磁金属阵列的布局形式[6,7]，但是这种方法没有用到优化问题的灵敏度信息，需要耗费较大的计算成本[8]。另一种设计方法是基于均匀化思想，将类周期电磁金属阵列等效为阻抗渐变的超表面，但这种等效仅适用于阵列单元尺寸远小于入射电磁波长的情况[9]。并且，由于趋肤效应导致的电磁金属结构的边界敏感性问题[10]，等效后优化结果的性能与实际物理结构的性能存在偏差，仍然需要借助电磁场全波分析方法对优化结果的物理布局形式进行再次修正设计，而这种设计同样受制于计算成本问题[11]。

通常，认为优化问题的灵敏度信息是高效优化算法的基础。有限差分法是求解灵敏度信息的最直接方法。虽然这种方法易于实现，但它有两个缺点。首先，有限差分法在处理大规模问题时需要耗费相当大的计算成本。即若要计算目标函数对m个独立设计变量的灵敏度，至少需要进行m+1次电磁场全波分析。这一问题对于类周期电磁金属阵列布局设计问题来说尤为严重。另一个问题是，利用差分法计算得到的灵敏度依赖于在各设计变量中设置的微小扰动值。王奇等[12]提出了一种基于阵列单元转角设计的强耦合阵列天线布局优化设计方法。该方法以电磁场全波矩量法为基础[13]，通过构造合理的坐标变换形式，利用伴随法解析推导了阵列域电磁辐射场对于阵列单元的转角变量的灵敏度信息。刘书田等[14]提出了一种面向类周期复合材料单元尺寸设计的灵敏度分析的映射方法，尽管这种映射方法最初是针对弹性力学均匀化问题而发展的，但它在处理类周期电磁金属阵列方面也表现出了应用潜力。

本文针对类周期电磁金属阵列的布局设计问题，提出一种基于坐标映射的灵敏度分析方法。通过构造基于坐标映射的电流场基函数模型，由虚拟的阵列单元映射出参数化的类周期电磁金属阵列布局形式，将阵列域的电磁性能变换为在虚拟的单元域内进行求解，以实现类周期电磁金属阵列的快速参数化建模及阵列布局设计的灵敏度分析。数值算例结果表明，该方法能够实现准确且快速的灵敏度信息求解计算。

2 参数化模型

2.1 映射变换

(1a)

(1b)

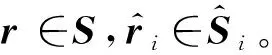
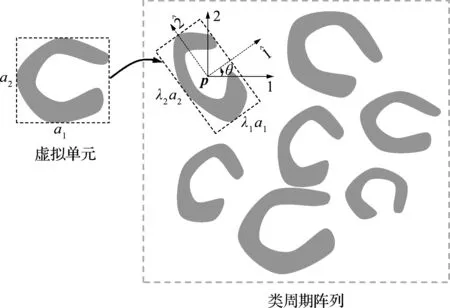
图1 坐标映射法示意图

2.2 参数化控制方程

基于矩量法体系框架[13]，根据映射变换，构建参数化的电场积分方程,

(2)

(3)

基于伽辽金方法[15]，结合理想电边界条件，N元类周期电磁金属阵列的参数化控制方程可用矩阵形式表示为

(4a)

(4b)

(5a)

(5b)

(5c)

文献[16]表明，采用插值法能够有效计算相似形状单元域内各点之间的距离，此处本文仍然将其表示为向量形式，以便于后续的灵敏度推导。采用式(5)计算出Zi i ′和Vi后，通过求解式(4)就可以得到类周期电磁金属阵列的未知表面电流J。

2.3 计算辐射电磁场

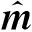
(6)

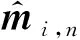
(7a)

(7b)

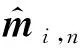
(7c)

式中Nl为虚拟单元域内的边元总数。值得注意的是，对于远场辐射问题，式(7)可以根据远场假设进行简化以加速求解[13]。

3 灵敏度分析

鉴于雷达散射面积σ是类周期电磁金属阵列布局设计的重要指标，以该指标作为目标函数对布局参数的灵敏度进行推导。

(8)

根据链式法则，σ相对于μ={λ,θ,p}的导数为

(9)

采用伴随法[18]进行灵敏度分析，有

(10a)

Z†γ=-(∂σ/∂J)†

(10b)

式中†为共轭转置算子，γ定义为待求解的伴随向量。∂σ/∂μ和∂σ/∂J计算如下,

(11)

根据式(6,7)定义的E和Ji ,n之间的线性关系，∂E/∂J可简化为

∂Ei ,n/∂Ji ,n=Ei ,n/Ji ,n

(12)

计算出∂E/∂J后，可通过求解式(10b)的伴随方程得到伴随向量γ。

至此，还需要推导出∂E/∂μ，∂Z/∂μ和∂V/∂μ以完成灵敏度分析。根据式(6，7)，有

(13)

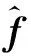
(14a)

(14b)

(14c)

(14d)

(14e)

(14f)

式中diag(*)定义为以向量*为对角元的矩阵，I为单位矩阵，0为零矩阵。对于二维问题,

(15)

提出的基于坐标映射的类周期电磁金属阵列布局设计的灵敏度分析的求解步骤总结如下。

(1) 定义虚拟单元域，并对其进行网格剖分。

(2) 定义式(1)的映射变换矩阵。

(4) 集成参数化控制方程(4)，求解得到J。

(5) 根据式(6，7)计算辐射电磁场。

(6) 根据式(8)计算目标函数。

(7) 根据式(10b)求解伴随向量γ。

(9) 计算由式(10a)定义的灵敏度信息。

4 数值结果

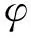
图2 类周期电磁金属阵列布局形式

分别采用提出的映射法和差分法对类周期阵列的布局参数进行灵敏度分析，对比结果如图3所示。结果表明，采用两种方法得到的结果具有很好的一致性。在计算成本方面，差分法需要进行m+1次全波分析以完成灵敏度分析计算，其中m为布局参数数目(对于此数值算例m=500)。而所提出的方法仅需要两次全波分析，一次用于求解控制方程，另一次用于求解伴随方程。差分法计算所需时间为140.32 min，而映射法仅需要2.52 min。验证了所提出的方法比差分法更加有效，尤其是对于具有大规模独立设计变量的类周期阵列布局设计问题。

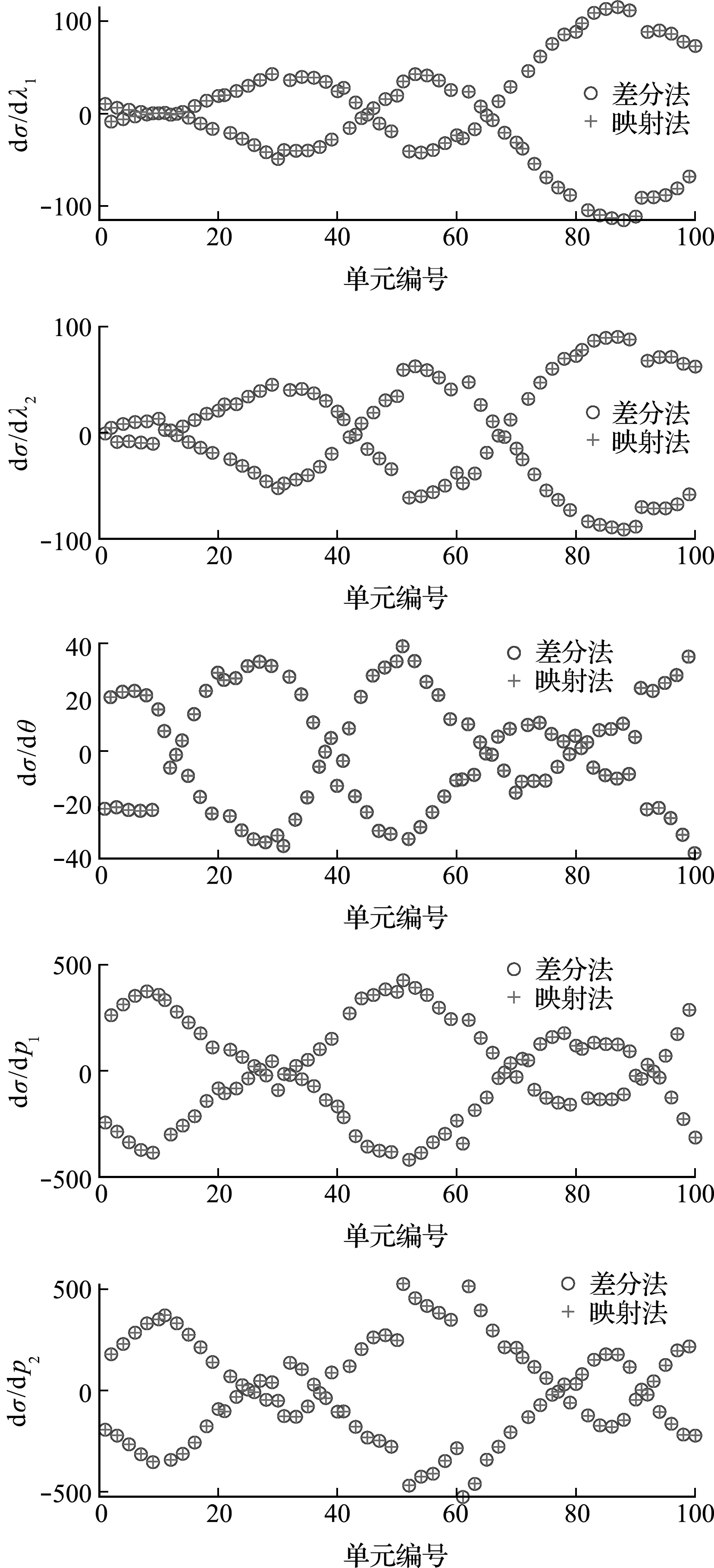
图3 映射法与差分法灵敏度分析数据对比

5 结 论

本文提出了一种基于坐标映射的类周期电磁金属阵列布局设计的灵敏度分析方法。通过构建合理的坐标映射模型，将阵列域的电磁性能变换为在虚拟的单元域内进行求解，实现了类周期电磁金属阵列的快速参数化建模及阵列布局设计的灵敏度分析。数值结果表明，与差分法相比，所提出的方法能够得到准确的灵敏度分析结果，且计算成本大幅降低。该方法可应用于求解类周期电磁金属阵列布局设计问题，以提升优化问题的求解效率。