基于边界位移的复合材料力学参数无损反演方法

赵冬梅， 邓建伟， 孙 直， 梅 跃

(大连理工大学 工程力学系 工业装备结构分析国家重点实验室，大连 116024)

1 引 言

非均质材料的反演已经在很多领域有重要应用。如在临床医学领域[1]，可实现肿块的诊断以及治疗，因为肿块通常比周围的生物组织更硬，所以通过对生物组织的材料参数反演，可对肿块定性表征。在生物力学领域中，细胞内部的不均匀材料分布能直接反映细胞的力学行为，而细胞的力学行为对于细胞的分化与迁移有着重要的影响[2]。

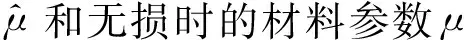
目前求解反问题的方法主要有两种，一是基于优化的有限元更新法[4,5]，通过全场测量技术获得在某种载荷情况下的测量位移场，根据经验设置初始假设的材料力学参数值，利用有限元法模拟获得模拟测量位移场，优化离散有限元模型中每一结点的力学参数，并不断迭代，直到含有全场测量位移的目标函数最小化。二是虚场法[4,6]，利用全场测量技术获得结构的变形信息，将人为构造满足运动许可的虚场和测量位移场代入虚功方程，对反问题进行求解，不需要迭代，求解十分迅速。这两种方法可用于多种本构，不仅可以反演线性材料参数，也可以反演非线性、超弹性[7]和各向异性材料参数。现在可通过全场位移反演出正交各向异性独立的四个材料参数[7-10]。

上述两种方法都需要获取结构的变形信息，因此实际测量位移的精度会影响反问题的求解精度，实际测量位移的误差越大，反问题的求解难度也随之加大。全场测量技术的高速发展[11-13]为精确测量位移值提供了技术支持，从而提高了反问题求解结果的精度。上述方法依赖精确的全场测量位移，但全场位移较难获取且结构内部的位移测量精度低。因此，本文提出基于边界位移的反演方法求解反问题[14,15]，此方法仅利用结构表面位移信息，就能够重建结构的材料参数分布。相对于测量全场位移，边界位移的测量精度高且测量方式丰富。

2 研究方法

2.1 有限元更新法

本文采用的主要研究方法是基于边界位移的有限元更新法。该反演算法的主要思想是将反问题转化为带有约束的优化问题来进行求解。其优化列式为

(1)

给定n组测量边界位移数据场，使目标函数最小化，求解得到剪切模量的分布。

本文采用几种不同的优化方法对其目标函数进行求解，一是结点优化，即对离散模型的每一结点的材料参数都进行优化；二是厚度方向上优化，即已知在轴向上的材料均匀分布，优化厚度方向上的材料参数；三是已知各层材料厚度后，优化各层的材料参数。本文研究方法流程如图1所示。

2.2 伴随法

本文利用基于梯度的Limited-BFGS Method(Limited Broyden-Fletcher -Goldfarb -Shanno Method)求解约束优化问题[16]。基于梯度的优化方法在每次迭代过程中都需要目标函数的值及目标函数关于未知材料参数的梯度。对于离散问题域，必须在每个结点处计算出目标函数的梯度。

图1 反演算法流程

将式(1)简写为

(2)

式中Reg(βm)为总变差递减正则化(TVD)，βm为未知材料参数。求目标函数对每一个未知材料参数的梯度,

(3)

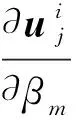
(4)

式中K，U和F分别为整体刚度矩阵、位移矢量以及外力。直接求解目标函数对材料参数的梯度需要对每一结点的目标函数都进行梯度求解，需求解大量的正问题，计算量非常大。因此，本文采用伴随方法高效求解目标函数的梯度。将式(4)代入式(3)得

(5)

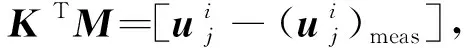
(6)

由式(6)可得，伴随法只需要在每次迭代时求解两次正问题，即可得到目标函数的梯度，计算效率显著提高。

3 算例分析

以复合材料层合板为研究对象，选用双层板作为分析对象，并假设每一层材料为均匀材料，且结构为可压缩材料，处于平面应变状态情况下。图2为该结构模型，在两层交界面上，材料是光滑过度，上层材料的剪切模量为6 MPa，下层材料的剪切模量为1 MPa，泊松比均为0.3。该模型在水平方向有81个结点，竖直方向上有41个结点，总共采用6400个线性三角形单元。

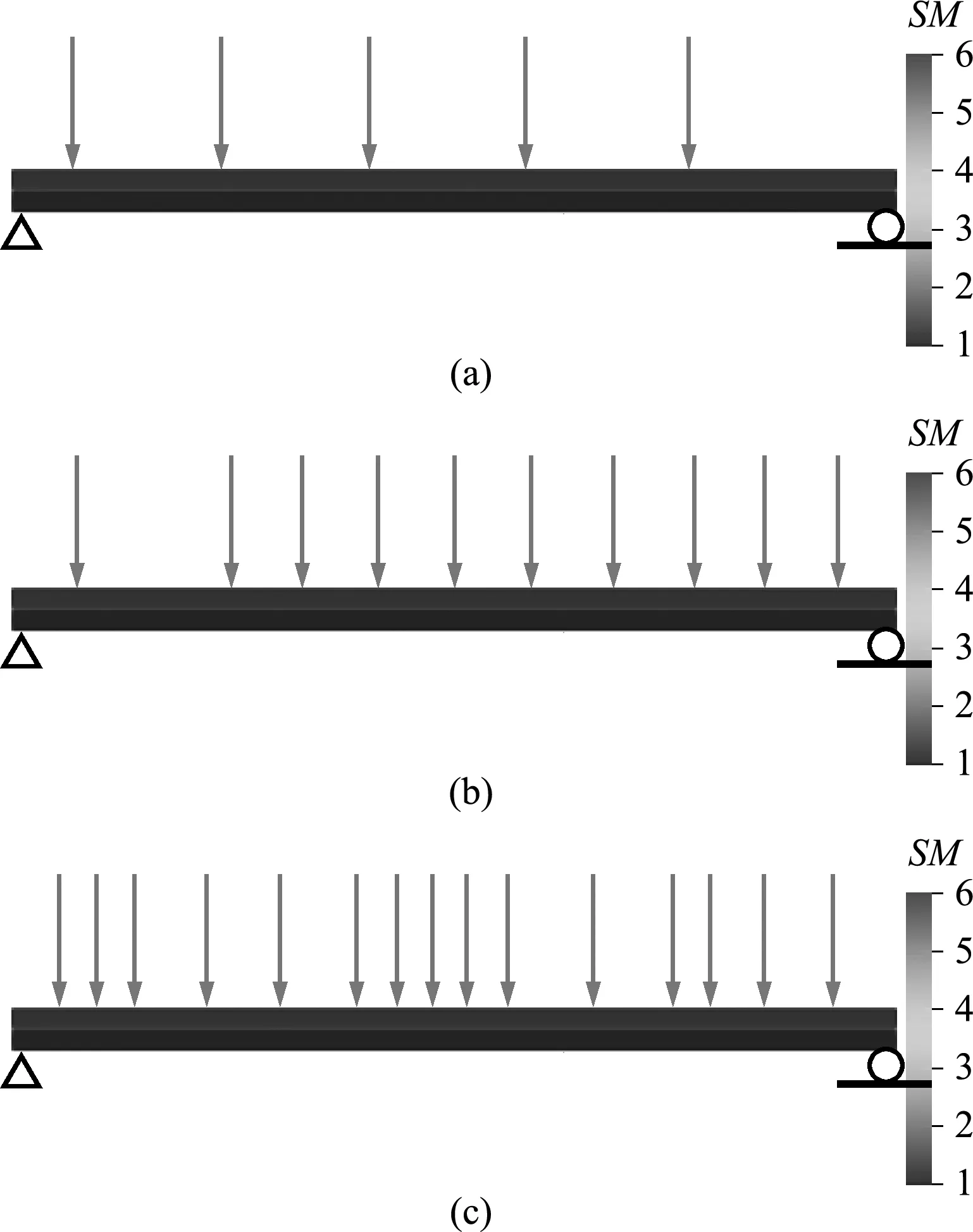
图2 目标剪切模量分布及施加载荷位置

图2分别采用了5个、10个和15个不同的边界位移组；图中SM为剪切模量，单位为MPa。本文通过有限元法求解正问题获取模拟的测量位移数据。在求解正问题时，模型底部左端为固定铰支，右端为可移动铰支；在模型顶部施加力载荷，一个箭头代表一个工况，即求解一次正问题可获取一组边界位移场。

考虑在实际情况下，测量位移不可避免地存在噪声。为了更好地模拟实际情况，在本文求解正问题所得的位移场数据中分别加入0.1%，1%以及5%的高斯白噪声，噪声水平的定义为

(7)

本文分别利用5组、10组和15组边界位移场进行反问题求解。图3是对每一结点优化，非均质剪切模量分布的重建结果。图4显示在已知轴向上的材料均匀分布，在厚度方向上优化反演的剪切模量分布。图5是已知材料厚度后，材料剪切模量的重建结果。图3～图5中，第1行～第4行分别为无噪声、0.1%，1%和5%噪声水平的重建结果。

利用式(8)定义剪切模量的相对误差为

(8)

表1～表3分别为图3～图5的误差分析。

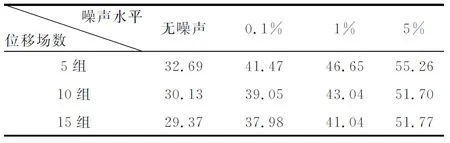
表1 结点优化的重建剪切模量相对误差 (单位：%)

从图3和表1可以看出，在同一位移场下，随着噪声水平的增加，反演的剪切模量值远离目标剪切模量分布，反演的分层界面处也越来越不光滑。在没有噪声的情况下，随着位移场数的增加，反演剪切模量值与目标值相差不大，材料交界处趋于目标分布。在5%噪声水平情况下，5组位移场下反演结果分层并不明显，10组和15组位移场下的反演结果分层情况更为明显，但整体的反演剪切模量值都偏大，这可能是噪声过大造成的。

图3 结点优化的剪切模量重建结果

图4中，在无噪声和0.1%噪声水平情况下，整体来看，分层情况与目标分层非常接近，反演剪切模量值也比较接近目标的剪切模量分布。在1%和5%噪声水平情况下，反演结果的层数可得到是两层，但每层材料的厚度反演结果恶化。从表2误差分析可以看出，厚度方向上优化较结点优化误差值明显降低。

图4 厚度方向上优化的剪切模量重建结果

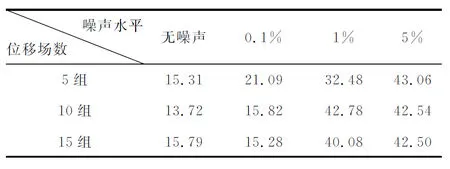
表2 厚度方向上优化的重建剪切模量相对误差 (单位：%)

图5中，在1%和5%噪声水平情况下，反演剪切模量的最大值与目标值有微小差异。但在所有噪声水平情况下，整体来看分层情况与目标分层非常接近，反演剪切模量值也比较接近目标的剪切模量分布。由表3可知，所有噪声水平下的误差明显降低很多。

从图3～图5可以看出，反演结果均出现了分层现象，图3的分层不如图4和图5明显；并且在 图3 左右两端边界位置反演的分层情况较差，反演的剪切模量值也存在较大误差；图5的反演结果分层情况是最接近目标分布的。在已知材料厚度的情况下，反演的剪切模量值和分层情况最为精确。在同一噪声水平下，随着位移场数的增加，重建的剪切模量值愈接近目标值；随着噪声水平的增大，反演结果中的材料界面分层处变得越来越不光滑，重建的剪切模量值远离目标值。

图5 已知各层材料厚度的剪切模量重建结果

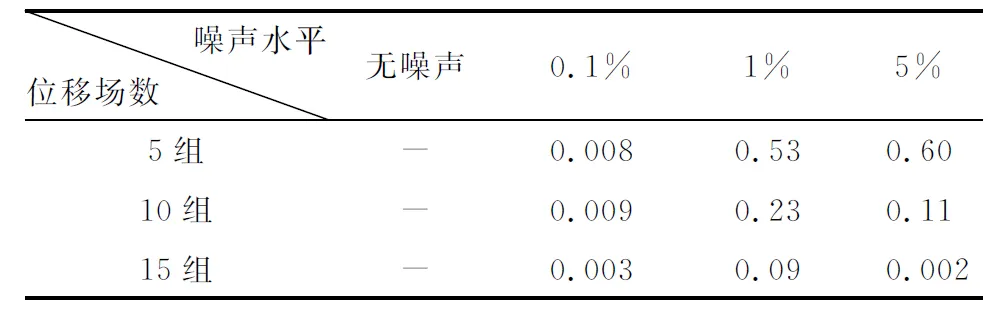
表3 已知各层材料厚度的重建剪切模量相对误差 (单位：%)

4 结 论

首先，本文仅利用边界位移场即可较为精确地反演复合材料的非均质材料参数分布，且随着位移场数的增加，反演结果会越来越接近目标值。其次，在分析的三种情况下，结点优化的误差整体最大；已知材料各层厚度的优化方法误差最小。综上，本文方法可以在结构全场位移难以测得时为复合层合板材料参数识别提供新的参考方法。

基于复合材料的力学参数识别，可进一步对其进行损伤识别及结构安全性评价。本文的研究结果对复合材料的无损检测以及损伤识别提供了新的思路。未来将通过实验测得的边界位移场数据对算法进一步测试。