基于模态参数灵敏度的损伤方程组求解正则化方法研究

孙健敏， 李 丹*， 颜王吉

(1.合肥工业大学 土木与水利工程学院，合肥 230009;2.澳门大学 智慧城市物联网国家重点实验室，澳门 999078)

1 引 言

损伤识别是结构健康监测的关键问题之一，近年来，基于振动的结构损伤识别一直受到广泛的关注[1-3]。由于频率和振型测试简单便捷，基于模态参数的损伤识别方法应用最为普遍。这些方法按照是否需要有限元模型可以分为无模型和基于模型的结构损伤识别方法。无模型的损伤识别方法通过结构损伤前后不同状态下的模态参数或相关衍生量构造损伤指标，进行损伤识别[4,5]。这类方法通常只能确定结构是否发生损伤和损伤位置，不能用于结构损伤程度量化。

基于模型的结构损伤识别方法，往往需要基于模态参数及其衍生量灵敏度建立结构损伤方程组，通过求解损伤方程组识别结构损伤位置和损伤程度[6,7]。由于实际工程中模态参数不完备性和噪声的影响，结构损伤方程易出现病态问题，对这一问题直接求解可能产生错误的结果[8]。为了解决这一问题，正则化方法引入到结构损伤方程组的求解过程，以确保识别结果的正确性。Ren[9]提出了基于模态参数的损伤方程组求解的奇异值截断算法，并用简支梁进行了验证。Weber等[10]将Tikhonov正则化(或称L2范数正则化)方法用于两层框架结构的损伤识别中，证明了该方法可以有效地解决结构损伤识别中的病态问题。这一方法在无噪声或噪声很小时才能达到较好的效果。为了进一步提高抗噪能力，Li等[11]在此基础上对Tikhonov正则化方法进行改进，验证了不同噪声水平下的结构损伤识别结果优于Weber的方法。正则化参数控制了正则化问题的数据保真度与解之间的平衡，对识别结果具有重要影响。一些学者提出了偏差准则、L曲线和广义交叉验证(GCV)等方法[12]，这些方法依据穷举思想，计算耗时且难以选择最优参数。近年来，Bayes系统识别理论框架受到了广泛关注[13]。Jin等[14,15]基于分层贝叶斯推理提出了自适应确定正则化参数的贝叶斯正则化方法，并证明该方法与Tikhonov方法引入了相同的正则化项。Chen等[16]将贝叶斯正则化方法用于结构模型修正中，对基于模态参数的结构损伤方程组进行了求解，结果表明，该方法具有较高的计算效率和较好的鲁棒性。

Tikhonov正则化方法倾向于产生超光滑解，导致损伤识别结果分布在许多结构单元上。实际工程结构的损伤通常只发生在几个单元或构件上，即损伤具有稀疏性。周述美等[17]提出了使用L1范数正则化方法求解结构损伤方程组，利用频率和振型数据对空间桁架结构进行了有效的损伤识别。骆紫薇等[18]对灵敏度矩阵各列进行范数归一化，进一步提高了L1范数正则化求解结构损伤方程组的计算效率和鲁棒性。然而，由于没有闭合解，L1正则化参数的选择十分受限。针对该问题，一些学者对L1正则化参数的选择进行了相关研究，提出了结合L曲线与偏差原理的方法[19]和摩擦模型启发式方法[20]。除以上常用方法外，Sarmad等[21]提出用LSMR-Tikhonov混合方法求解基于柔度灵敏度的损伤识别问题，该方法在迭代过程中选择一个最优正则化参数，而不需要先验参数。文献[22，23]对稀疏贝叶斯学习在损伤识别中的应用进行了详细的研究，证明了该方法在求解损伤识别反问题中的优势。此外，还有列主元QR分解[24]，L1/2范数正则化[25]和改进的加权迹稀疏正则化[26]等方法均用于结构损伤识别。

虽然各种正则化方法在结构损伤识别中得到广泛应用，但是其原理、区别和联系及其在结构损伤识别中的适用性没有系统的研究和对比。本文从基于模态参数灵敏度的损伤方程组出发，梳理奇异值截断算法、L2范数正则化、贝叶斯正则化及L1范数正则化方法的基本原理、区别和联系。通过连续梁和框架结构数值算例，讨论损伤程度、噪声水平和测点数目对几类方法识别结果的影响，对比几类正则化方法在结构损伤识别应用中的适用性。

2 基于模态参数的结构损伤方程组

对于一个具有N个单元的无阻尼线性系统，其结构特征方程可以表示为

KΦr=λrMΦr

(1)

在实际工程中，通常假定结构发生损伤时质量矩阵不发生变化，即损伤仅引起结构刚度变化。基于结构有限元模型，损伤结构的刚度矩阵可表示为

(2)

式中Kd为结构损伤后的整体刚度矩阵，Ki为i单元对整体刚度矩阵的贡献，Δαi为单元损伤指数，表征i单元的刚度损失。

根据特征灵敏度的代数表达式[27]，不考虑质量变化时，特征值和振型关于设计参数pi的灵敏度为

(3)

由一阶泰勒级数展开，可得第r阶特征值和振型的改变量为

(4)

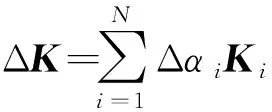
(5)

使用结构的m阶特征值和振型进行计算，可将式(5)写成矩阵形式

SΔα=ΔR

(6)

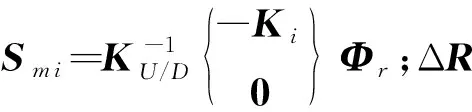
3 正则化方法理论基础

3.1 奇异值截断算法

奇异值截断算法可以减少式(6)的参数空间，使结构损伤方程组变得数值稳定。根据矩阵的奇异值分解，灵敏度矩阵S可以分解成两个正交矩阵U，V和奇异值矩阵Σ的乘积，

(7)

(8)

由式(7，8)可以看出，小奇异值对灵敏度矩阵S贡献较小，而对最小二乘解Δα影响较大。因此，可以去除小奇异值，从而提高解的稳定性。截去第k个奇异值得到方程的解，

(9)

3.2 L2范数正则化方法

正则化技术可以通过在反问题中引入先验信息，对病态问题进行鲁棒逼近。这一方法通过添加解的范数项引入先验信息，L2范数正则化方法通过惩罚项(或称为正则化项)对目标函数进行限制,

(10)

式中第一项表示残差范数，第二项表示解的范数。γ为正则化参数，用于控制残差范数和解的范数之间的平衡。当γ=0时，上述问题即为最小二乘问题。该最小化问题具有解析解，

Δα=(SST+γI)-1STΔR

(11)

式中I为单位矩阵。根据灵敏度矩阵的奇异值分解，将式(7)代入式(11)可得

Δα=V(Σ2+γI)-1ΣUTΔR=

(12)

3.3 贝叶斯正则化方法

L2范数正则化参数的选择通常采用GCV和L曲线等方法，计算耗时且难以选择最优参数。为了避免正则化参数选择的问题，基于分层贝叶斯思想提出了贝叶斯正则化。对于本文线性方程组求解问题，假设噪声误差为ε，即ΔR=SΔα+ε，引入分层贝叶斯推理,

(13)

(14)

(15)

式中Ns为用于计算的每阶振型元素个数。

(16)

(17)

(18)

(19)

图1 贝叶斯正则化流程

3.4 L1范数正则化方法

L2范数正则化方法对不适定问题的求解往往过于平滑，这意味着预测的损伤通常可能分布在附近的结构单元上，与实际的结构损伤情况不相符。因此，对解加入具有稀疏性的限制更符合损伤识别的应用，式(10)的最小化问题可以转化为

(20)

当0≤p≤1，这类问题的解具有稀疏性质。当p=0时，L0范数表示非零解的个数，这保证了问题的稀疏性。然而，L0范数是不连续的，求解该问题需要进行大规模的组合搜索，通常在计算上不可行[28]。当0≤p<1时，这类问题是非凸问题，而p=1时，该问题可以转化为凸优化问题，因此在引入稀疏性的应用中最为广泛。这一方法称为L1范数正则化方法，其形式为

(21)

3.5 几类正则化方法的联系与区别

对比式(9,12)可知，奇异值截断算法与L2范数正则化方法在本质上是统一的，其采取了不同的措施以减少灵敏度矩阵的小奇异值对应项对病态方程组解的影响。奇异值截断法完全消除了小奇异值对应项对解的影响，而L2范数正则化将奇异值对应项乘以小于1的系数，对小奇异值项的影响进行较大程度的折减。由式(10,16)可知，L2范数正则化和贝叶斯正则化对解的限制在本质上都是加入L2范数正则化项，但贝叶斯正则化可以通过迭代自适应求解正则化参数，避免了传统正则化参数选择方法耗时和易产生局部最优的问题。

L2和L1范数正则化加入不同形式的正则项，L1范数正则化能产生更稀疏的解，可以从几何角度解释。如图2所示，假设Δα含有两个分量，即Δα1和Δα2，式(20)第一项的解集是在(Δα1,Δα2)空间上的一组等值线，如图中阴影区域所示。第二项为加入的L2范数或L1范数约束集，分别为图2圆形和菱形等值线。式(20)的解需要在残差范数项和正则项之间平衡，即解出现在两项的等值线相交处，交点的位置通过正则化参数γ控制。采用L2范数时，图2中两项等值线的交点通常在某个象限内，即Δα1和Δα2均非零，而采用L1范数时，两者的交点通常在坐标轴上，即Δα1或Δα2为零，这就导致L1范数正则化相比于L2范数正则化易产生更稀疏的解。另外，L1和L2范数正则化易方法可以嵌入贝叶斯框架，即在进行最大后验概率估计时，L1范数正则化假设未知参数Δα服从拉普拉斯先验分布[29]，而L2范数正则化假设其服从高斯先验分布。在零值点，拉普拉斯分布曲线更陡，而高斯分布更平坦。因此，L1范数正则化期望许多解为零，而L2范数正则化假设解随机分布在零左右[30]。

图2 L2和L1正则化原理

4 数值模拟及对比研究

4.1 连续梁

4.1.1 模型简介

图3 连续梁有限元模型

4.1.2 无噪声损伤识别结果

取连续梁的前三阶竖向振动频率和振型对不同损伤工况进行识别，无噪声的损伤识别结果如 图4 所示。可以看出，在无噪声条件下，几类正则化方法均能准确地识别结构损伤位置，L2范数正则化和贝叶斯正则化在损伤识别中易产生假阳性单元，奇异值截断算法次之，而L1范数正则化仅产生少量假阳性单元(指实际无损伤却判断为发生损伤的单元)。随着损伤单元的增加，几类方法识别的假阳性单元数量增加，且程度增大。

4.1.3 噪声的影响

为了分析噪声对结构损伤识别的影响，本文将参与计算的频率和振型按如下方式添加噪声[18]，

(22)

图4 无噪声条件下连续梁损伤识别结果

本文考虑了5%,10%和15%噪声水平的影响，不同噪声水平下，工况3的损伤识别结果如 图5 所示。随着噪声的增加，几类方法识别结果中出现的假阳性单元数量和损伤程度增加。噪声水平达到15%时，L2范数正则化识别结果中出现超过实际损伤的假阳性单元，其他几类方法仍能准确识别损伤位置。

为了衡量几类方法对损伤程度识别效果的优劣，引入以下相对误差,

(23)

为了避免仅根据一组加噪后的观测数据进行识别的随机性，在每一噪声水平下对工况3采用50组加噪数据分别进行损伤程度识别，取其最大相对误差的均值，结果如图6所示。可以看出，奇异值截断算法、L2范数正则化和贝叶斯正则化识别结果误差均随噪声水平的增加而增大，其中L2范数正则化增大最快，贝叶斯正则化次之，奇异值截断算法相对较慢，而L1范数正则化方法识别结果最大相对误差变化不大，具有更好的鲁棒性。需要指出的是，本文鲁棒性是指正则化方法在噪声变化和测点数目改变等影响下识别损伤能力的好坏，通过识别损伤位置的偏差、产生假阳性单元的数量和损伤程度的误差大小进行评价。

图5 噪声影响下连续梁工况3的损伤识别结果

4.1.4 测点数目的影响

实际工程结构通常受到传感器数目的限制，测试的自由度不完整，为了研究测点数目对识别结果的影响，对连续梁选择不同的测点数目[28,26,…,10]进行损伤识别。在28个测点的基础上，每次在连续梁的两跨上对称位置减少2个测点，由支座向跨中位置依次间隔1个测点进行减少。首先在连续梁(图3)上除支座外的28个节点(节点2～节点15和节点17～节点30)上布置测点，在此基础上减少对称的2个测点(节点15和节点17)，得到26个测点，继续去除节点2和节点30得到24个测点。依此类推，得到22个测点(去除节点13和节点19)和20个测点(去除节点4和28)等测点布置情况。无噪声条件下，几类方法在不同测点数目下识别结果的最大相对误差如图7所示。可以看出，当测点数目减少时，L1范数正则化识别结果的最大相对误差稳定在20%左右，L2范数正则化和贝叶斯正则化识别结果的最大相对误差逐渐增大并出现错误。而本文选取奇异值截断的阈值为σi/σmax=0.005，奇异值截断算法受截断误差限取值影响较大，鲁棒性最差。

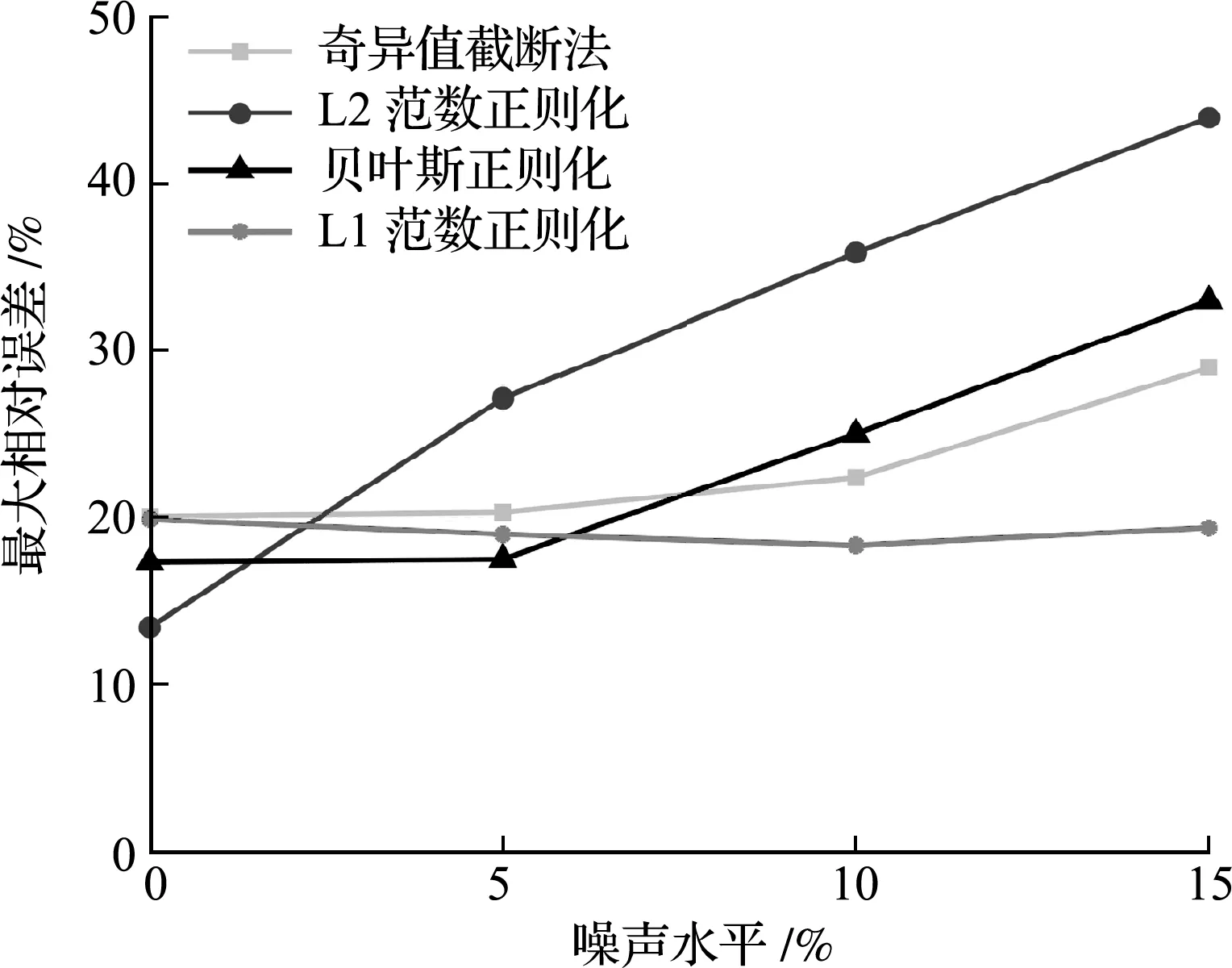
图6 连续梁工况3识别结果最大相对误差

图7 测点数目对连续梁识别结果的影响(工况3)

4.2 平面刚架

4.2.1 模型简介

为了进一步对比正则化方法在不同结构中损伤识别应用的效果，模拟如图8所示的平面刚架结构。每层刚架高1.5 m,宽3 m，共划分45个单元，其参数列入表2。假设该刚架单元8、单元32和单元43分别发生10%，15%和20%的损伤，取前六阶弯曲模态频率和振型作为输入进行损伤识别。

图8 平面刚架有限元模型

表2 平面刚架参数

4.2.2 损伤方程归一化的影响

由于频率和各阶振型的量级范围不同，直接采用式(6)进行求解，可能使得频率和各阶振型所占权重差别过大，从而影响识别结果。为了平衡计算过程中频率与各阶振型的权重，可以对结构损伤方程进行归一化处理，

(24)

图9给出了平面刚架结构归一化前后采用几类正则化方法的识别结果。可以看出，各方法求解未归一的损伤方程出现了明显的识别错误，而经过归一化处理的方程识别结果有了明显的改善。因此，对损伤方程进行归一化处理能够有效地提高损伤识别的准确性。此外，归一化处理能够有效地提高贝叶斯正则化和L1范数正则化方法的计算效率。这一处理对连续梁结构同样适用。

图9 归一化前后平面刚架损伤识别结果

4.2.3 损伤识别结果

不同噪声水平下，刚架结构的损伤识别结果如图10所示。无噪声条件下，几类正则化方法能够准确识别损伤的位置，但L2范数正则化对损伤程度的识别效果稍差。随着噪声的增加，各方法识别的假阳性单元逐渐增多。当噪声水平达到5%时，奇异值截断算法对损伤位置的识别出现错误；噪声水平达到10%时，L2范数正则化识别结果出现超过实际损伤的假阳性单元，贝叶斯正则化识别结果也出现较多接近实际损伤的假阳性单元。当噪声水平达到15%时，几类方法都出现了不同程度的识别错误，损伤程度较小的单元难以得到识别。

图10 平面刚架损伤识别结果

无噪声条件下改变测点数目，对平面刚架结构进行损伤识别，发现奇异值截断算法首先出现识别错误，L2范数正则化和贝叶斯正则化方法随着测点减少误差逐渐增大，而L1范数正则化方法在测点数目较少时，识别误差也稳定在20%以下，这与连续梁的结果一致。综合连续梁和平面刚架结构在噪声水平和测点数目变化等方面的分析，可得几类方法的对比结果(表3)。

表3 几类正则化方法的对比结果Tab.3 Comparison of several regularization methods

5 结 论

本文系统地梳理了几类正则化方法的原理、区别和联系，利用连续梁和平面刚架结构数值算例对几类方法在基于模态参数灵敏度的损伤方程组求解中的适用性进行了对比分析。主要结论包括：

(1) 无噪声条件下，L2范数正则化和贝叶斯正则化在损伤识别中易产生假阳性单元。随着损伤单元的增加，几类方法识别的假阳性单元数量增加、程度增大。

(2) 随着噪声水平的增加，几类方法识别结果产生的假阳性单元数目和程度增加；奇异值截断算法和L2范数正则化方法易出现识别错误，而贝叶斯正则化稍好，L1范数正则化在噪声水平较高时仍能够准确地识别损伤位置，且产生少量假阳性单元，抗噪效果最好。

(3) 随着测点数目的减少，L1范数正则化能够较准确地识别损伤位置和程度，贝叶斯正则化次之，而L2范数正则化较早出现明显的误差，奇异值截断算法受截断误差限的影响最易出现识别错误，鲁棒性最差。

(4) 损伤方程的归一化处理能够有效地改善频率和各阶振型所占权重不同对识别结果的影响，提高损伤识别的准确性。