地震作用下水库坝体与水体相互作用数值模拟

许 栋, 梁心雅， 许航维, 李健增, 及春宁

(天津大学 水利工程仿真与安全国家重点实验室，天津 300072)

1 引 言

中国是世界上水坝数量最多的国家，也是环太平洋火山地震带上地震多发国家。地震不仅引起水坝坝体振动，还会进一步诱发坝后水体波动，形成作用于坝体的动水压力和坝-水耦合作用[1-2]，影响坝体安全。

水中结构物在地震激励下的动力响应属于流固耦合力学问题，相关应用多集中于水库坝体和跨海桥梁工程等。在桥梁动水作用方面，柳春光等[3]综述了近年来跨海桥梁的地震动水效应的研究进展；李忠献等[4，5]通过辐射波浪理论求解地震动水压力，结合波浪绕射理论分析了桥梁在地震和波浪联合作用下的动力响应；江辉等[6]利用波、流和地震共同作用双向流固耦合计算模型研究了不同波流参数下跨海桥梁深水桥墩的地震响应特征；郭庆康等[7]比较了势流理论和粘性流体理论下地震不同输入方式对有限元模拟的影响；林曾等[8]基于波浪力的Morison分析发现动水压力明显增大了深水桥墩的地震响应幅度；吴安杰等[9]研究了地震激励下桩柱震动引起的水面波动时程，认为波流作用对深水桥墩地震响应的影响范围可达 -31.6%～63.5%。对于水库大坝的地震动水作用，相关研究主要集中于水体对坝体表面的动水压强分布[10-12]和水体加速引起的附加质量力(Added Mass Force)[13-15]，对于超高坝体还需考虑水体的压缩性[1,15]。研究方法主要包括模型实验[13,16]、时域和频域理论分析[17-19]及数值模拟[20-23]。王铭明等[24]以某重力坝为原型建立坝体-水体系统模型试验，并将结果与附加质量模型和流固耦合有限元模型结果比较，发现附加质量法夸大了水体对坝体结构的动力响应；Zhou等[13]的模型试验动水压强的分布与Westergaard[14]的理论模式基本符合；宫必宁[25]在大型地震模拟振动台施加人造地震波和El.Centro地震波，研究重力坝的动力响应；Zhou等[26]利用能量变分原理，通过Rayleigh-Ritz方法推导出系统的本征频率方程，在数值水槽中研究了垂直矩形板一侧与水接触时振动受水深和密度比等因素的影响；陈怀海等[17]利用级数展开和线性叠加原理 ,给出了一种求取弹性坝面动水压力影响系数矩阵的数值算法；Demirel等[21]基于虚网格浸入边界法(Ghost-cell immersed boundary method)、Behroozi等[18]采用无网格(mesh-free method)法模拟了坝体振动激励下的水动力过程，为揭示坝-水耦合作用机制提供了依据。

坝体振动引起的水波和动水荷载问题，本质上与推波板造波原理类似，这方面的研究可借鉴数值波浪水槽的相关成果。在数值波浪水槽推波板造波方面，Romate[27]通过吸收开边界条件以及高阶边界元方法模拟非线性波；周斌珍等[28-30]基于势流理论和时域高阶边界元方法建立非线性数值波浪水槽模型实时模拟造波板运动生成波浪；Wu等[31]利用一端可以造波的有限三维水池模拟波浪与浮体之间的非线性相互作用。水库床面振动引起的上层水体剪切运动与波浪边界层发展类似，相关分析可以借鉴有关波浪边界层的理论研究成果[32，33]。

目前对大坝受地震激励下动力响应特征，多集中在水体压力和结构响应方面，对于坝体振动引起的水体波动，以及波动对水体压力荷载和库区地面振动影响等认识还不全面，已有相关理论分析多忽略水体的非恒定波动过程。本文建立坝体动边界条件下的二维数值波浪水槽，利用数值模拟研究坝体振动诱发的水面波高、波能以及动荷载等问题，探究地震波能量和水深改变对坝-水相互作用的影响规律，分析库区地面振动对近底水体的影响强度。

2 动边界水体运动数学模型

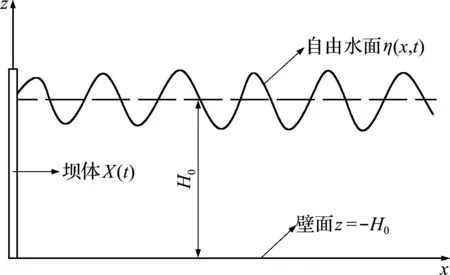
图1 动边界水体运动模拟的数值波浪水槽

基于计算流体力学软件FLUENT建立模拟模型，其中水流运动的连续性方程为

(1)

式中ux为水平方向速度，uz为竖直方向速度。

水流运动的动量方程为

(2)

(3)

坝体处水体运动与坝体振动速度相同，

X(x,t)=X(t)|x=0

(4)

水库底边界为不可滑移固壁边界,

ux=0,uz=0

(5)

自由水面模拟采用VOF(Volume of Fraction)方法[14-16]。根据对比粘性项的不同处理方法选用紊流模型。

3 数值模拟验证

水库坝体在地震波激励下振动所引起水体运动和水槽造波过程类似，为了验证数值模拟对水体运动、尤其是动边界引起自由水面波动的模拟能力，采用波浪水槽实测波高数据[26]验证数值模拟结果，水槽断面如图2所示，共设置线性波和非线性波两组模拟工况，模拟参数列入表1。

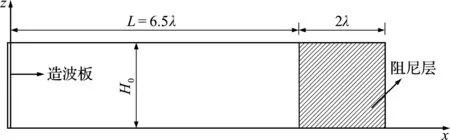
图2 造波水槽试验模型

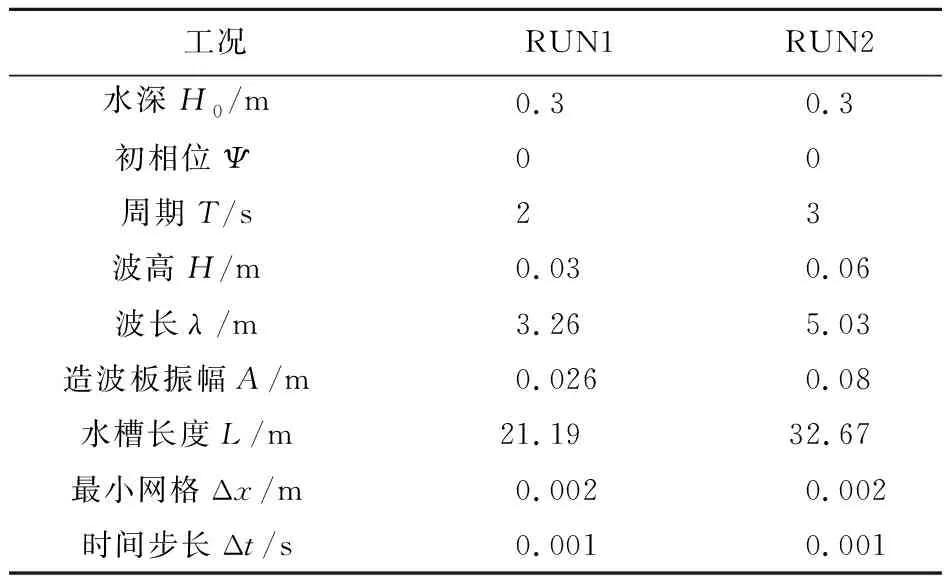
表1 验证工况模拟参数设置

造波板处采用动网格模拟坝体运动形成的动边界。对于粘性项处理，分别采用inviscid模型、Standardk-ε模型和Reynolds Stress模型，并根据模拟结果进行优选。

从模拟结果来看(图3)，波浪周期为2 s的线性波模拟，在x=7 m处，inviscid模型与Reynolds Stress模型和实验测量值最接近，波高误差在5%以内；Standardk-ε模型误差最大，达21.7%，如 图3 所示，波浪波高衰减显著，与该模型引入过大的紊动粘性有关。对周期为3 s的非线性波浪模拟工况也有类似的结果(图4)。Inviscid模型与Reynolds Stress模型波浪误差相差不大，为方便壁面切应力的计算，采用Reynolds Stress模型对地震波激励下的水库坝体周围水体运动进行模拟。

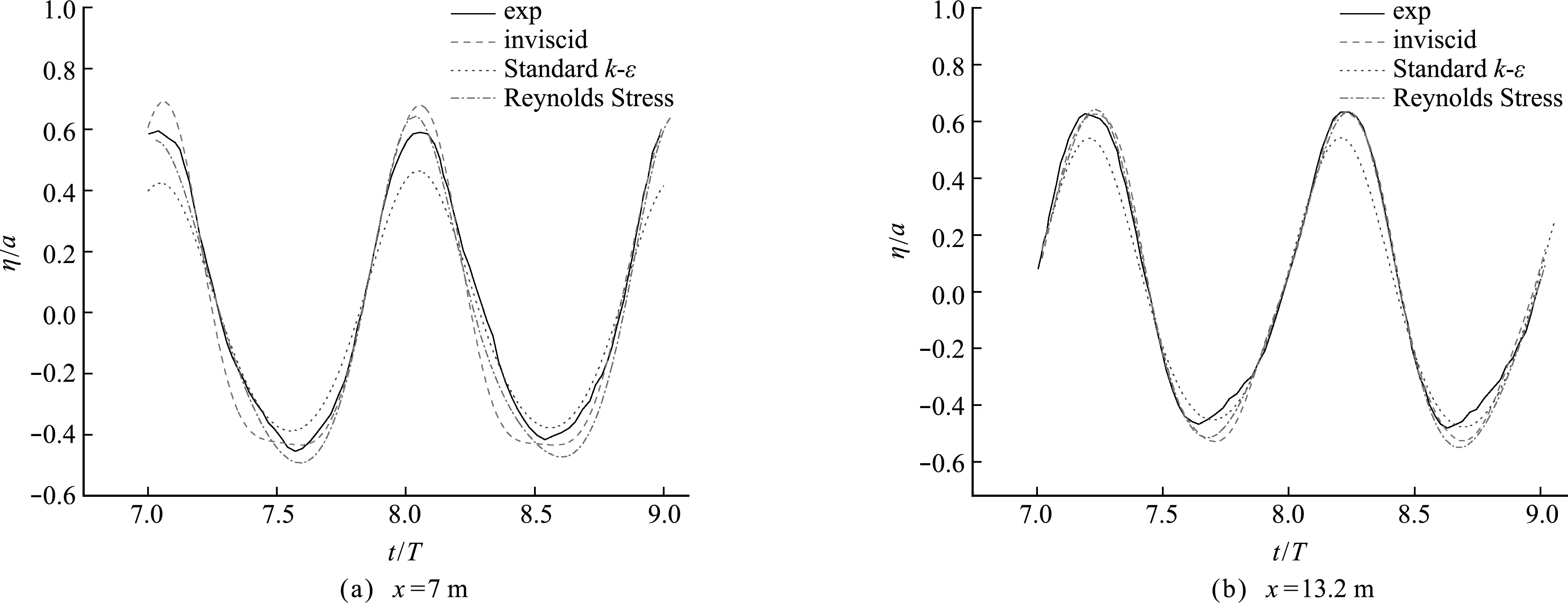
图3 工况RUN1不同位置波面历时曲线

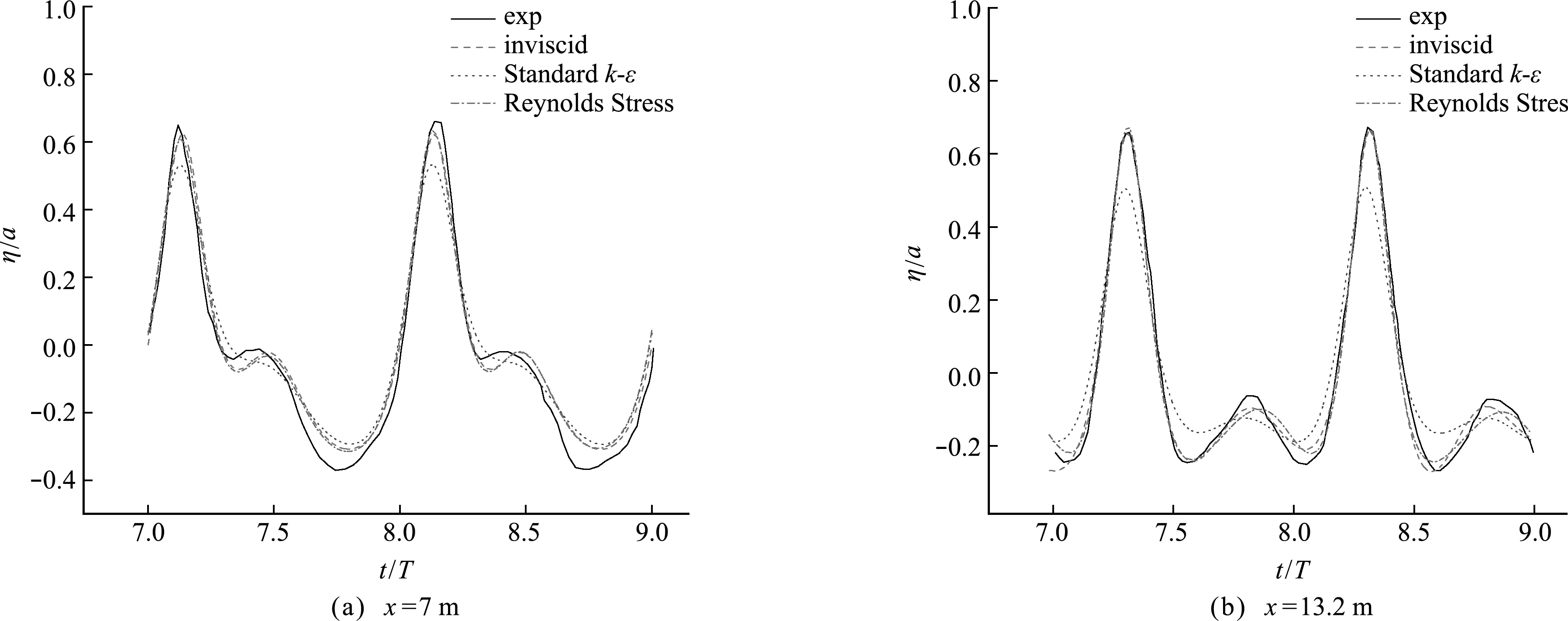
图4 工况RUN2不同位置波面历时曲线

3 地震激励下的坝后水动力模拟

3.1 计算模型和参数

建立立面二维数值水槽长为100 m，水深1 m～100 m，采用结构化网格，最小网格尺寸0.005 m，水面附加局部加密，最大细长比为10，如图5所示。

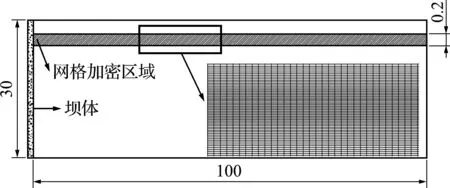
图5 计算区域及局部网格划分(单位：m)

为了模拟真实地震作用，选用Kobe地震波振动速度时程，将高频部分滤波处理后，施加在动边界上，如图6所示。

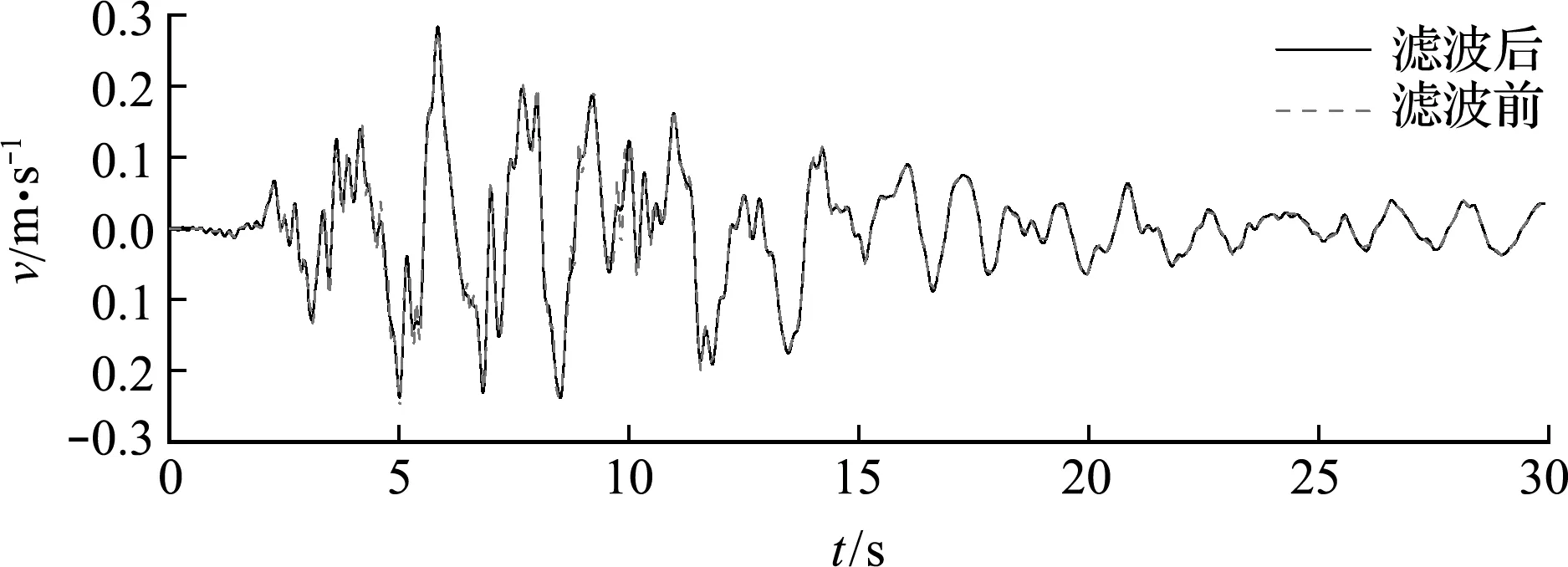
图6 动边界处Kobe地震波速度时程

3.2 模拟工况

根据水深H0、地震波相对振幅A/A0(A0为Kobe地震波原波幅)以及是否考虑地面运动三个要素组合，共设置11个模拟工况，参数设置列入表2。

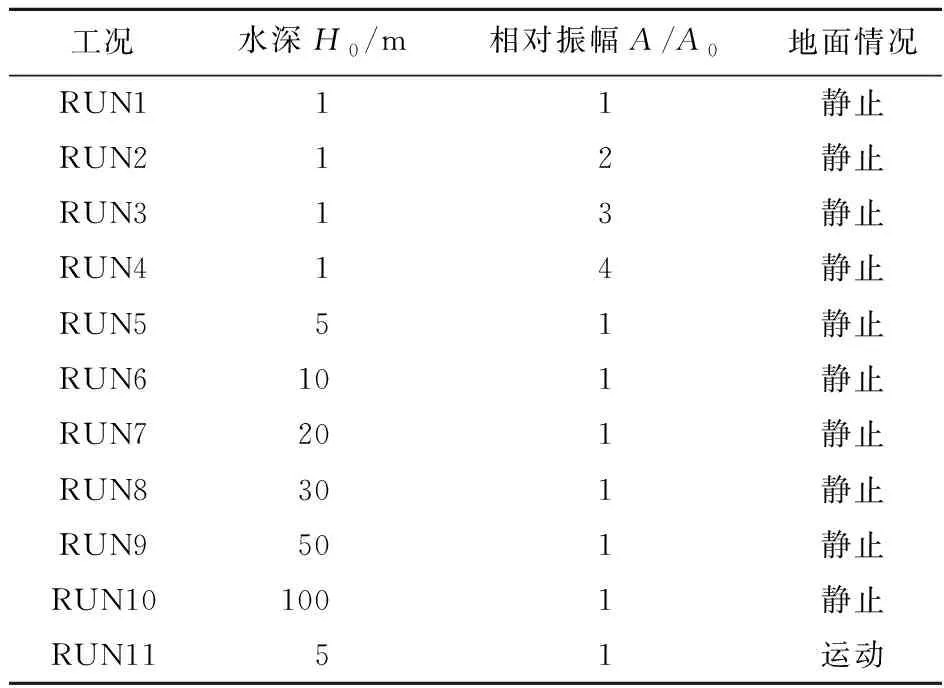
表2 数值模拟工况参数设置

4 模拟结果及分析

4.1 地震波振幅对坝后水体响应的影响

在坝体振动过程中，会引起坝后水体水位波动，并把部分能量传递给水体。为了探究地震波振幅变化对能量传递及最大波高的影响，分别取 Kobe 地震波以及将地震波波幅放大2倍、3倍和4倍，进行一系列数值模拟，获得不同时刻水面波动和速度剖面的变化过程。以工况RUN1为例，典型时刻的波面及部分波峰波谷处的流速矢量如图7所示。可以看出，坝体振动开始后，在坝后激发约6～8个较大幅度的水面波浪，波高历时和地震波引起的坝体振动周期基本吻合。在此之后，坝体振幅减小，所激发波高也逐步衰减，坝后水面恢复平静，而初始激发的大幅度波浪向水库方向继续传播。这意味着地震发生后，因坝体运动造成的动水作用会随着坝体振动的结束在近坝区域快速消失，其影响向水库深处持续传播。

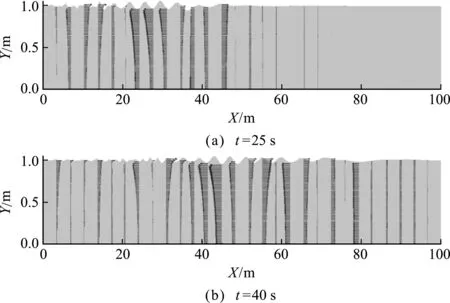
图7 工况RUN1不同时刻波面及波峰波谷流速剖面

利用平均波浪能量表征坝体传递给水体的能量，平均波浪能量指单位面积内的波浪能量，可计算为

(6)

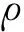
在相同水深条件下，不同振幅地震波激励下，坝体附近(x=0.5 m)和水库中间(x=50 m)处波面历时如图8所示。可以看出，不同地震波波幅激发的水面波动周期过程基本相同，这说明尽管实际地震波频率成分复杂，但激发的波浪要素仍然服从经典线性波的色散关系，波浪周期和波高无关。

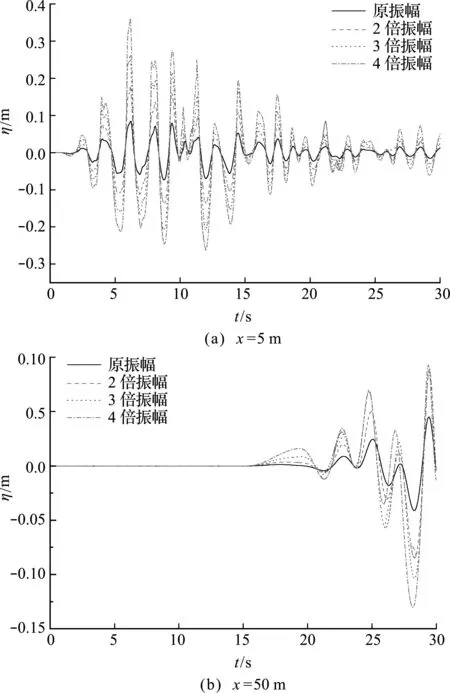
图8 相同水深不同振幅地震波激励下波面历时

随着地震波振幅增大，由坝体振动产生的波高变大。原始Kobe地震波在1 m深水池内激发的最大波高为0.084 m，为水深的8.4%；当地震波波幅增大至4倍时，激发的波浪波幅增大至0.36 m，为水深的36%。波能密度也存在类似的增长趋势，列入表3。综合模拟结果可以看出，坝体振动激发的波高与地震波振幅近似呈线性增长关系，如图9所示；坝体传递给水体的能量增长率略高于地震波振幅，如图9所示。考虑到在地震动历时不变的前提下，地震诱发坝体振动的速度变化幅度和坝体位移变化幅度趋势相同，可以认为波浪波高和波能与坝体振动幅度呈近似线性关系。

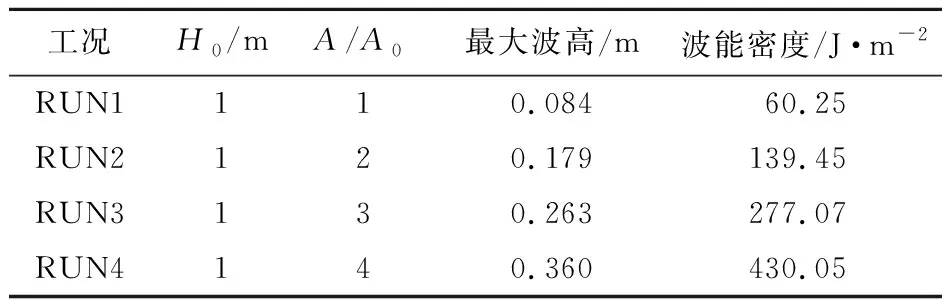
表3 相同水深不同振幅地震波激励下辐射波最大波高和平均波浪能量

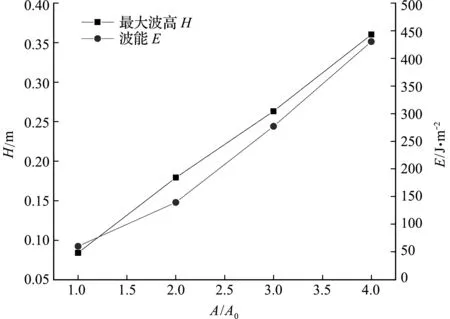
图9 地震波振幅对激发波浪最大波高和波能的影响

4.2 库区水深对坝-水相互作用的影响

设置7组不同水深的工况进行一系列数值模拟，研究水深对坝-水间相互作用的影响。模拟结果表明，当输入的地震波信息不变时，随着水深增大，由坝体振动产生的水面波高也会变大，最大波高随水深增长过程如图10所示。可以看出，当水深超过20 m之后，水深对地震激发水面波波高的影响明显减弱。在同样的地震波激励下，水深为100 m的水体产生的波高比20 m水深大25.5%，波高增长率随水深变深增大越来越缓。这说明波高和水深之间存在非线性变化关系。实际工程中的大坝一般高度较大，在地震-大坝-水动力综合模拟实验中，往往需要采用缩尺模型，在根据试验测量水面波高换算实际波高时，不能简单地采用几何相似比尺，需要考虑到波高随水深的非线性变化规律。从坝体-水体能量传输方面来看，随着坝高或库区水深增大，相同的地震动能够向水体输入更多能量，坝体振动激发的波能随水深变化呈近似线性变化。

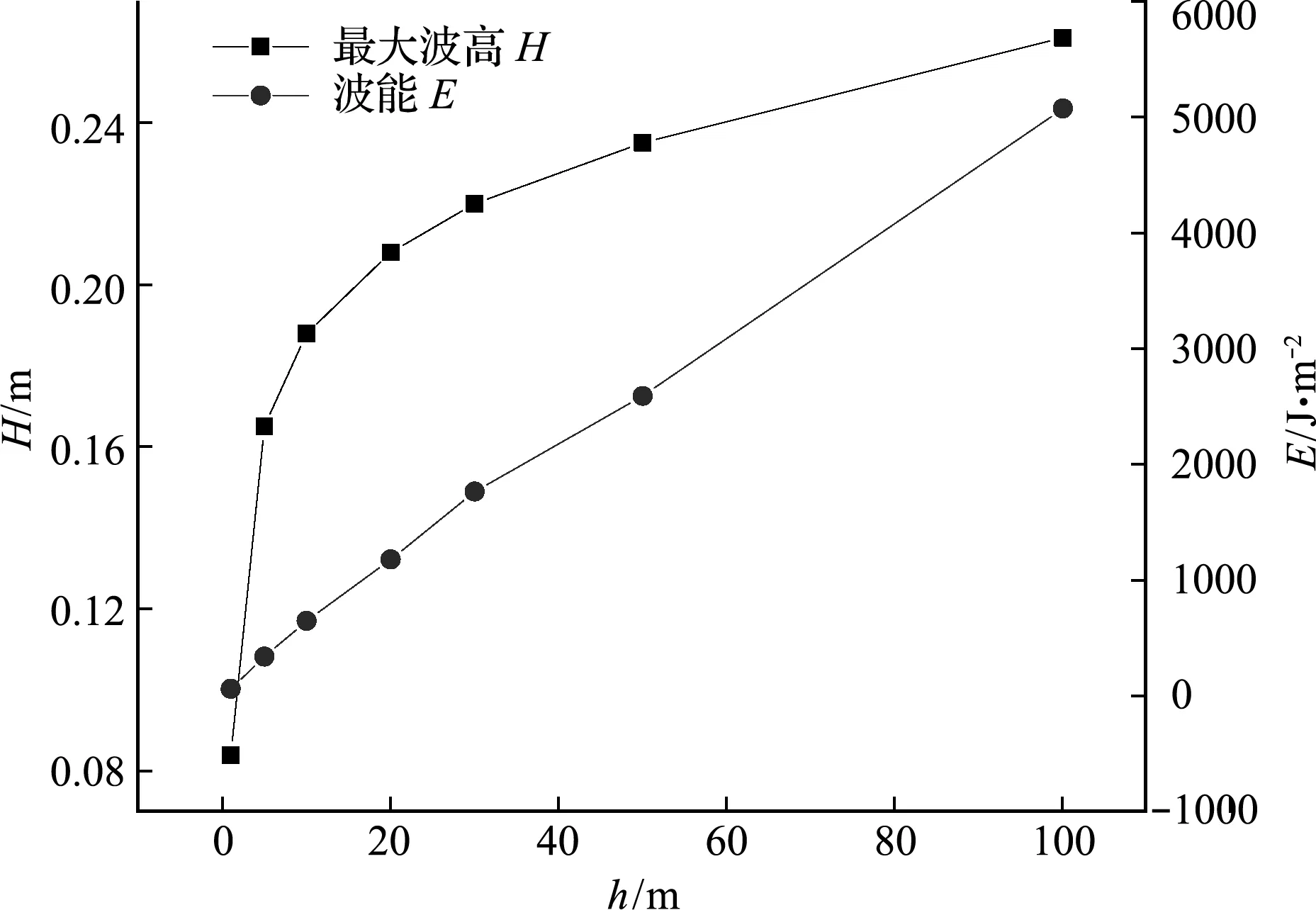
图10 水深对地震激发波浪最大波高和波能的影响

在不同水深条件下，相同地震动激励下坝体附近(x=0.5 m)和水库中间(x=50 m)处波面历时如图11所示。可以看出，水深越大，坝体振动激发的水体波动传播越快，这点与线性波理论中的波浪色散关系一致。当水深达到50 m后，水深继续增大对波动传播速度影响明显降低，这种情况类似于海洋的深水短波，波浪传播速度基本不受水深影响。

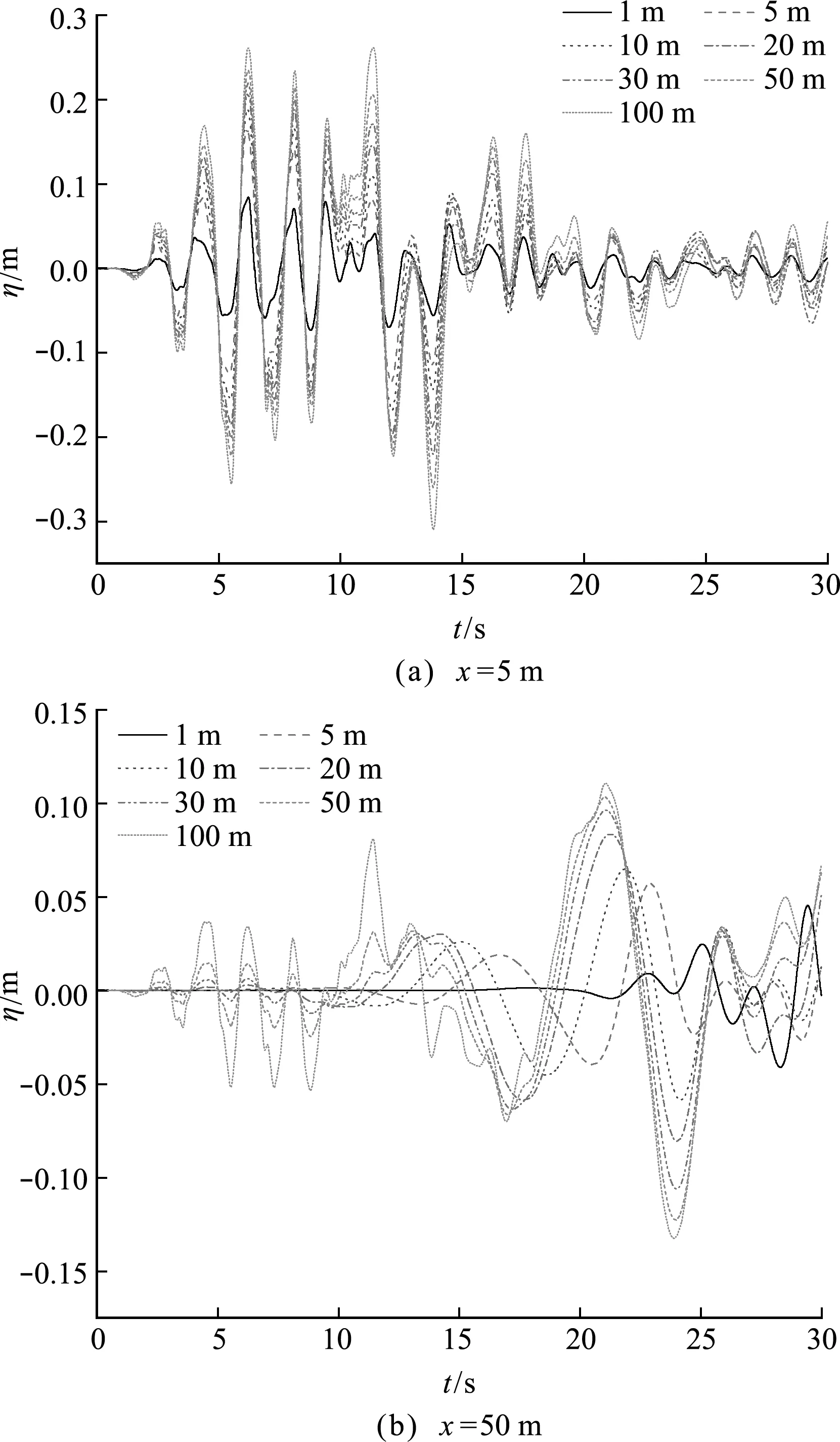
图11 水深对地震激发水体波面历时的影响

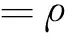
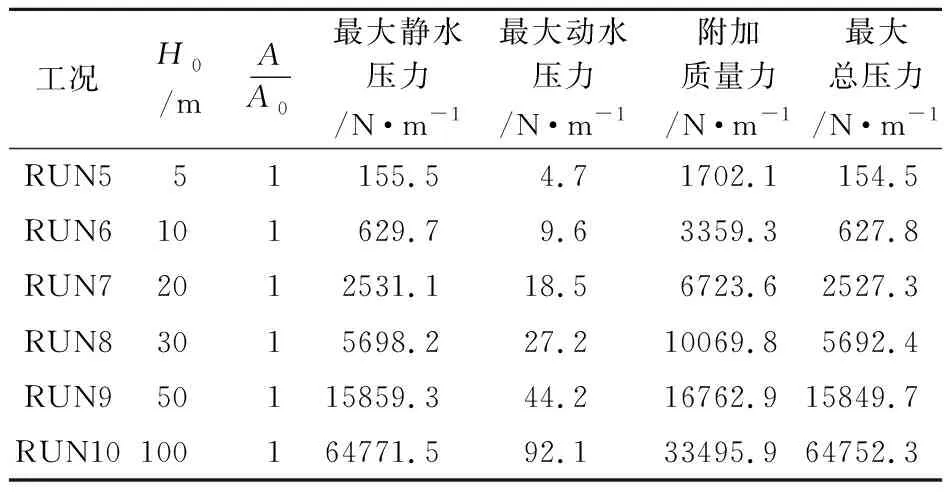
表4 不同水深相同振幅地震波激励下坝体受力情况

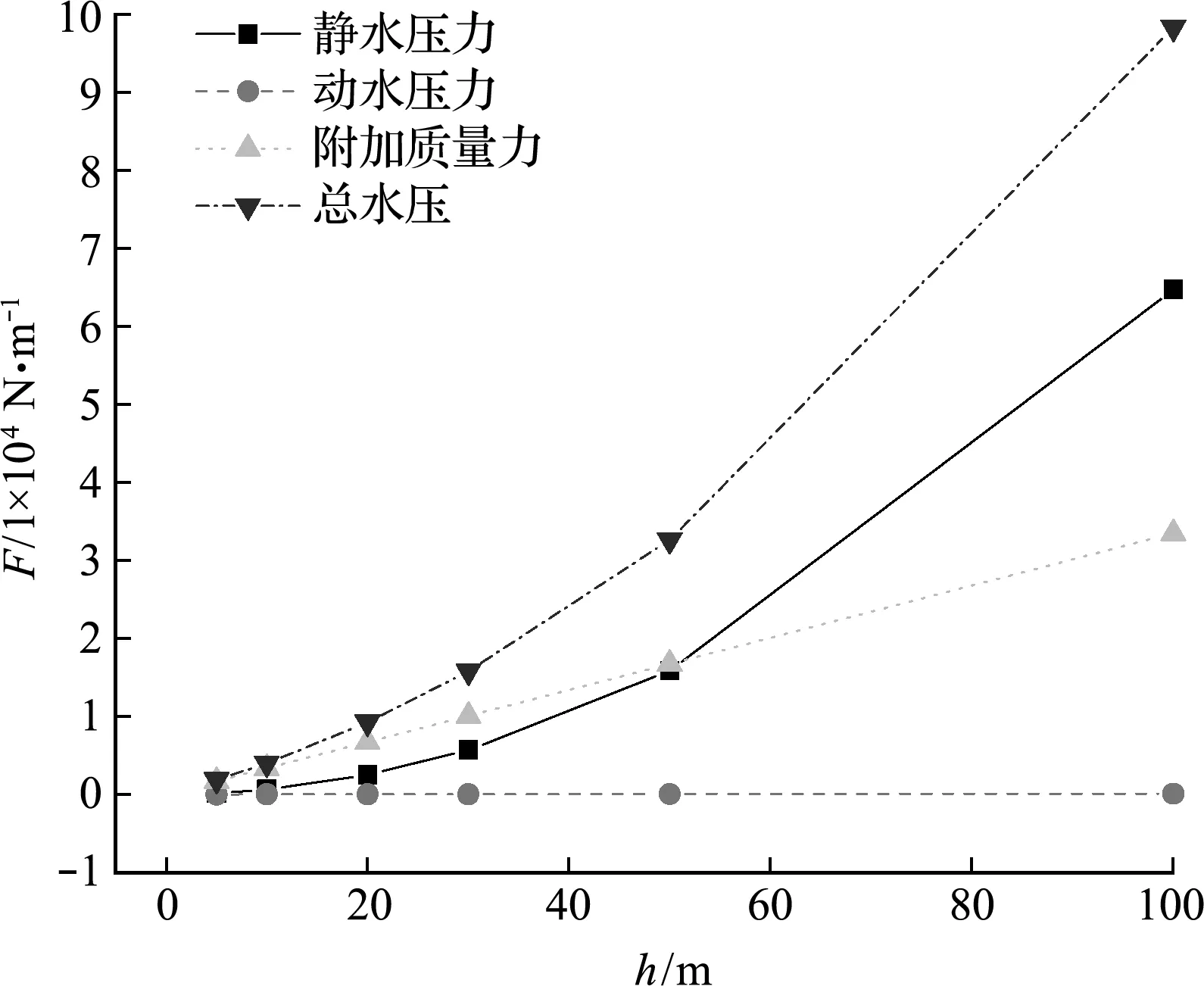
图12 坝体所受水压力与水深关系

4.3 库区水深对坝-水相互作用的影响

在实际的地震过程中，地震动不但引起坝体振动，库区地面也会发生水平晃动，形成对水体的周期性剪切动边界作用。为了弄清该剪切作用对水体运动的影响，模拟水深为5 m时地面受地震波激励条件下的水体，得到不同时刻水体流速剖面如图13所示。模拟结果表明，地面运动开始时，由于水体受到地面剪切力的作用，底层水体产生较大的水平速度，近底最大水流流速和地震动速度相当；在距地面 0.05 m 范围内，产生较大的流速梯度，尤其是距地面0.007 m范围内；距离地面0.5 m以上的上层水体几乎不受底部运动的影响，流速基本保持为0；距离地面0.05 m～0.5 m范围内的水体，流速梯度逐渐减小，流速逐渐降低为0，近底水体的剪切运动不会传递到上层水体。和水体运动相比，地震引起的地面震荡主要是高频运动，在近底产生类似震荡流边界层的结构，仅在底部非常薄的区域内存在较大的剪切速度。以本文Kobe地震波为例，产生的影响主要集中在距离地面约2%的底层区域，该区域的平均速率为v0=0.78 cm/s。其他大部分水体区域受地面振动影响微弱。

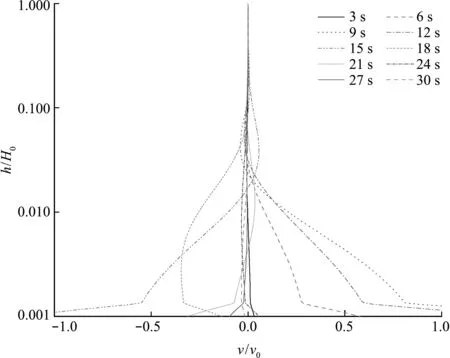
图13 地震引起地面运动形成的近底水体流速剖面

5 结 论

通过坝体动边界条件下的数值波浪水槽模拟，研究了在忽略坝体自身弹性变化的条件下地震波激励下的坝体-水体相互作用，结论如下。

(1) 地震发生后，坝体振动激发坝后水体波动，波动随着地震动结束在近坝区域快速消失，其影响向水库持续传播，部分振动能量向水体传递。

(2) 不同地震波波幅所激发的水面波动周期过程基本相同，波浪周期和波高无关。波高和波能与地震波振幅近似呈线性关系。

(3) 地震激发的水面波高和水深之间存在非线性变化关系，波高和水深呈增函数关系，当水深超过20 m后，水深对地震激发水面波波高的影响明显减弱。波能随水深变化呈近似线性变化。

(4) 坝体在振动过程中，受到水体静水压力、水体运动速度对应的动压和运动水体的附加质量力三部分作用力。其中速度水头对应的动水压力占比较小；随着水深增大，附加质量力呈线性增长，而静水压力呈非线性增长。水深50 m时，附加质量力和静水压力基本相同。

(5) 库区地面振动在水库底部引起震荡边界层，引起的水体运动主要局限在近底约0.05 m的范围内，对上层水体及水面波动影响微弱。