某通用飞机试飞中的长周期模态发散问题研究

李康孛

（中航通飞华南飞机工业有限公司研发中心总体部，广东 珠海 519040）

长周期模态本质上是空速和高度的振荡，其特征是飞机交替进行爬升和俯冲运动。在振荡过程中动能与势能相互转换[1]。由于这个模态的振荡周期通常很长，即使是轻微不稳定的，也不会显著增加驾驶员的操纵负担，因而常常在飞机研制中不受关注。

本文首先分析了23 部飞机的长周期模态特性的适航要求。对一种发动机安装在机身上方的高置发动机布局飞机的长周期模态开展了试飞研究，然而试飞结果中却显示出该飞机的长周期模态特性受动力影响显著，与常规飞机存在明显差异，因此对该问题进行了深入研究并找到的原因。该研究结论为解决长周期模态试飞出现的发散问题提供了解决思路，对类似高置发动机布局飞机的长周期模态稳定性设计具有借鉴意义。

1 设计要求

1.1 适航要求

适航规章CCAR-23-R3[2]第23.181(d)条款关于纵向长周期模态的要求是“考虑第23.175 条规定的状态，当保持飞机在偏离配平速度至少±15%的速度需要的纵向操纵力突然解除，飞机不得表现出任何危险特性或与解除的操纵力大小有关的过度响应。飞行航迹的任何长周期振荡不得出现不稳定导致驾驶员的工作负荷增加或危及飞机”。

咨询通告AC23-8B[3]对23.181(d)条的解释是：长周期模态通常是轻阻尼，有时甚至是不稳定的。只要不影响诸如在期望的速度配平、高度保持或者下滑跟踪等正常的飞行任务，适度的不稳定是可以接受的。有用的准则包括：如果周期不小于15 秒，则倍幅期应大于55 秒，否则振荡应该是接近中立稳定的。

1.2 军标要求

GJB 185-86《有人驾驶飞机（固定翼）飞行品质》[4]对长周期模态的要求是驾驶杆固持和松浮时，飞机的长周期速度振荡应满足下列要求：

标准1：阻尼比>0.04；

标准2：阻尼比>0；

标准3：倍幅时间至少为55s。

1.3 验证判据

通过长周期模态的适航要求和军标要求的对比分析可以确定适航要求与军标中的标准3 要求基本一致。由于长周期模态轻微不稳定对于飞行员操纵飞机的影响较小，适航规章对其要求较为宽松。因此，对于通用飞机，长周期模态试飞验证判据采用咨询通告量化准则：如果周期不小于15 秒，则倍幅期应大于55 秒，否则振荡应该是接近中立稳定的。

2 试飞状态和方法

2.1 试飞方法

对于长周期模态的试验，恰当的操纵控制输入应是一个相对缓慢的升降舵脉冲，使飞机在配平点的基础上增加或者减小速度。一旦速度产生偏离，操纵就要回复到初始位置并且松浮。因此试验按照如下程序进行：

（1）按要求的构形和状态下，配平飞机在稳定的直线飞行状态；

（2）缓慢拉杆改变空速至偏离配平速度约10%～15%的速度，然后纵向操纵力突然解除，激励飞机的长周期振荡；

（3）除非飞行速度和载荷系数或者其他限制有超出限制的危险，松浮操纵应保持足够长时间，并能够建立一条能确定半衰时（倍增时）的迹线。

2.2 试飞状态

按照适航要求，应该在所有检查过纵向静稳定性的形态和状态下对长周期模态稳定性进行检查，应该检查足够的状态以确定所有操作速度下都有可接受的特性。飞机长周期模态选取如下状态进行：

（1）爬升，速度1.3VS1，最大连续功率；

（2）低速巡航，速度1.3VS1，平飞功率；（3）高速巡航，速度VH，平飞功率；

（4）下降，速度1.3VS1，3°下滑功率；

（5）无动力着陆，速度VREF，慢车功率；

（6）带动力着陆，速度VREF，3°下滑功率。

3 试飞结果及分析

3.1 试飞结果

针对选定的6 种试飞状态开展长周期模态试飞，试飞结果如表1 所示。

表1 长周期模态试飞结果

试飞结果分析表明，在所有试飞状态下，长周期模态振荡周期均大于15 秒，倍幅时间均大于55 秒，符合适航要求。其中，高速巡航、无动力着陆和带动力着陆阶段长周期模态均是收敛的，低速巡航时近似中性稳定，爬升阶段呈发散现象。爬升阶段长周期模态振荡周期短且阻尼比最小，为临界状态。振荡周期和阻尼比随着空速的增大而增大，符合一般理论规律。

3.2 速度影响

取所有平飞状态的长周期模态测试点，绘制长周期模态振荡周期和阻尼比随飞行速度变化的散点图，并用最小二乘线性拟合，见图1。从图中可以看出，长周期模态的振荡周期和阻尼比均随着飞行速度的增大而增大，符合理论规律。

图1 长周期振荡周期和阻尼比随平飞速度的变化

3.3 动力影响

从表1 试飞结果对比中可以观察到，爬升状态、低速巡航状态和下降状态，仅发动机功率存在差异，导致长周期模态特性差异甚大。可以判断，飞机长周期模态的振荡周期和阻尼比，与发动机功率状态存在明显的关联性。

选取爬升、低速巡航、下降状态的不同功率状态的长周期模态试飞点样本，绘制振荡周期和阻尼比随油门位置的散点图见图2。从图中可以看出，振荡周期和阻尼比均随着油门位置（发动机功率）的增大而减小。

图2 长周期振荡周期和阻尼比随油门角度的变化

4 理论分析

该飞机的长周期模态受动力影响的现象与常规飞机相比有更加显著且是不利的[5]。有必要从飞行动力学原理上寻找到问题的原因。

基于小扰动理论，对飞机纵向运动方程进行线性化，然后忽略状态量导数α˙和q˙，得到长周期模态振荡频率和阻尼的近似计算公式，见公式（1）和公式（2）。过程详见文献[6]。

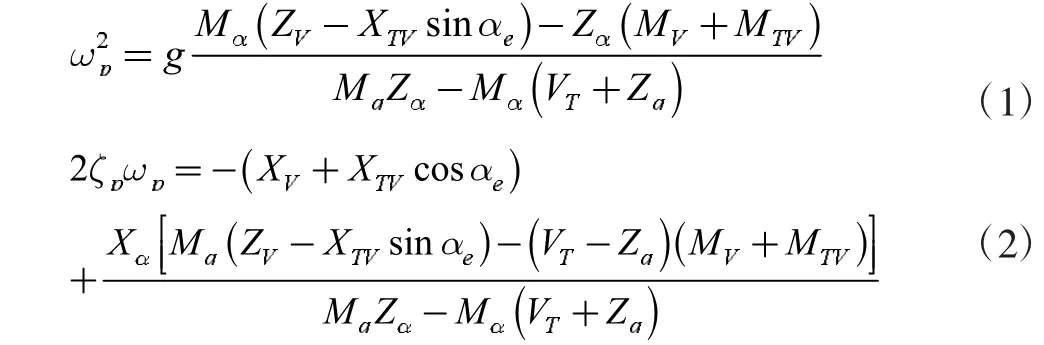
基于常规飞机的气动导数的符号和量级对上述公式进行参数影响分析如下：

（1）公式（1）中导数Mq、Zα、Mα是负值，VT是正值且VT>>Zq。因此，公式（1）和公式（1）中分母项MqZα-Mα（VT+Zq）为正；飞行时由于平衡迎角αe很小，因此可忽略XTVsinαe项。因此，基于公式（1）中可以判断长周期模态振荡频率将随参数（MV+MTV）的增大而增大。

（2）公式（2）中导数XV、XTV为负，且XV>>XTV；导数Xα为正，导数Mq、ZV为负值，VT是正值且VT>>Zq。结合公式（1）的部分分析结果，可以从公式（2）中判断长周期模态的阻尼将随（MV+MTV）增大而减小。

公式（3）和（4）是MV和MTV的表达式。对于低速通用飞机，导数CmV通常可以忽略，则MV的大小和正负取决于稳定平衡飞行时的气动俯仰力矩系数Cm；发动机螺旋桨拉力T通常随空速增加而减小，则MTV的大小和正负取决于拉力线的到重心的距离h。

该飞机为高置发动机布局（见下图3 所示），距离h 是负值且较大。在稳定飞行状态下，为了维持俯仰力矩平衡，需要一个较大的抬头力矩系数Cm去平衡发动机拉力产生的低头力矩，这就导致MV为正值。

图3 某通用飞机侧视图

另外，由于发动机和螺旋桨推力随空速的增加而减小（见图4），所以距离h 是负值也导致MTV是一个正值。并且导数（MV+MTV）随发动机功率或拉力增大而增大。最终导致飞机长周期模态特性受发动机功率影响显著，在大功率爬升状态时，长周期模态振荡频率更高且阻尼更小。

图4 螺旋桨拉力随空速的变化

因此，经过上述理论研究和分析，飞机的长周期模态在爬升阶段频率更高、阻尼更低的问题原因已经确定。对这种飞行动力学特性的更加直观的过程描述是：

（1）当飞机保持配平状态飞行时，为了维持平衡迎角和升力，由于发动机拉力产生了显著的低头力矩，需要与之相等气动抬头力矩维持俯仰平衡。

（2）当飞机受到扰动进入俯冲空速增加时，气动抬头力矩增大而发动机拉力减小致使飞机产生的抬头力矩，抬头力矩使飞机迎角和升力系数增大，再加上动压增大，使得升力大于重力，最终导致飞机抬头进入爬升减速。

（3）飞机爬升过程中空速逐渐减小时，气动抬头力矩减小而发动机拉力增大致使产生的低头力矩，低头力矩使得飞机迎角升力系数减小，再加上动压减小，使得飞机升力小于重力，最终导致飞机低头进入俯冲加速。

（4）上述俯冲加速和爬升减速过程随着长周期速度振荡周而复始。

对于拉力线经过重心附近的常规飞机，长周期速度振荡过程中迎角基本为常数，即升力系数不变，升力因动压变化而变化。但对于高置发动机布局的飞机，长周期速度振荡时，飞机迎角随俯仰力矩周期性变化的影响不可忽略迎角和升力系数的周期性变化产生了额外的升力变化，这种激励使得长周期速度振荡更加趋于发散。该分析结论得到图5 的爬升阶段试飞数据的证明。

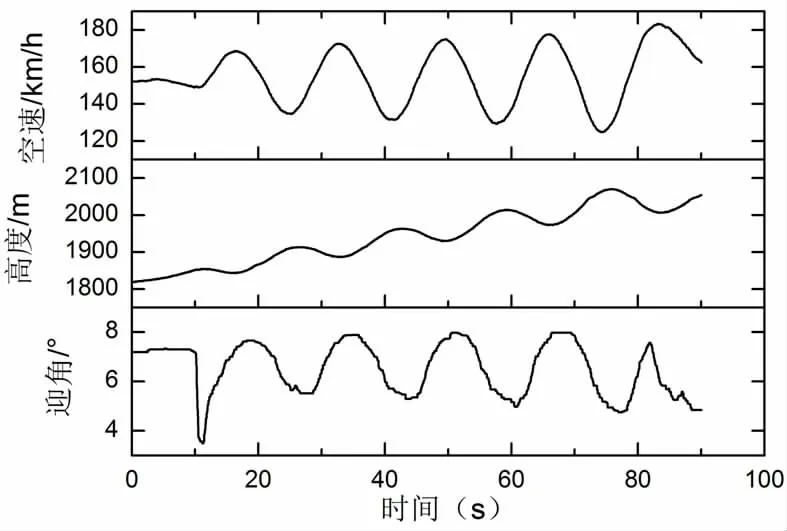
图5 爬升阶段长周期振荡时间历程

事实上，由于该飞机螺旋桨滑流会影响平尾的气动效能，且螺旋桨法向力起稳定作用，导致纵向静稳定性随拉力系数Tc增大而增强（见图6）。即导数CmV的为正值。也对长周期模态也同样产生一定的不利影响。

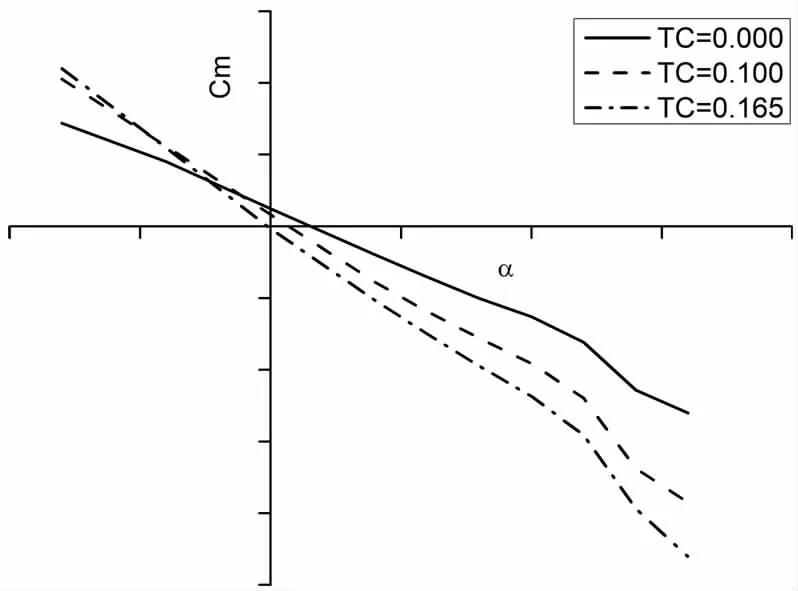
图6 俯仰力矩系数随迎角的变化（风洞试验）

基于上述研究结论我们可以合理地解释为什么临界状态在小速度且大功率的爬升状态。也可以进一步推断，飞机在后重心时由于纵向静稳定性更低，俯仰力矩的扰动影响将更加剧烈。因此，长周期模态会变得更差。这也得到了试飞证实。

5 结论

对于高置发动机布局的飞机，发动机拉力会产生显著的低头俯仰力矩，需要气动抬头力矩平衡，再加上拉力随速度的变化特性，使得飞机迎角随速度周期性变化，对长周期模态起到激励作用，导致其更加的不稳定趋势。

该飞机出现的爬升状态长周期模态，虽然最终通过调整重心后限符合了适航规章的倍幅时间不小于55 秒的要求。但从飞行员的角度，长周期响应在无意或注意力分散的操作中很重要，振荡发散特性并不是一个良好的设计，飞机设计时应该尽力避免。对于同类高置发动机布局的通用飞机，本文研究的长周期模态特性受动力影响而恶化问题值得关注和借鉴。