采用U型谐振器的小型化带阻滤波器设计

许 晗

(黎明职业大学 信息与电子工程学院，福建 泉州 362000)

随着通信技术的飞速发展，关于平面滤波器的研究逐渐受到国内外学者的广泛关注，其中，带阻滤波器作为一种能滤除干扰信号、提升电路性能的器件，在电路中的作用日益凸显，各种结构的带阻滤波器被不断提出。常用设计带阻滤波器的方法有增加缺陷地结构[1-3]、加载谐振器结构[4-6]、信号差分技术[7]、交叉耦合技术[8]、信号干涉技术[9-10]等。文献[3]提出了一种由3个W型缺陷地结构级联的带阻滤波器，该滤波器的工作频率范围在2.6～3.4 GHz，相比于传统的缺陷地带阻滤波器具有更宽的阻带带宽和较小的带内插入损耗，滤波器的尺寸为0.25λg×0.67λg。文献[4]中利用方形谐振器设计出一款中心频率为5.7 GHz的带阻滤波器，该滤波器带有3个传输零点和4个传输极点，相对带宽为46.11%且具有较好的带内插入损耗，但通带内的回波损耗还有待优化，且滤波器尺寸较大，为0.49λg×0.41λg。文献[10]提出了一种基于槽线结构的信号干涉带阻滤波器设计，此滤波器阻带内有两个传输零点，具有较好的带阻抑制性能，过渡带的陡峭程度也得到了一定的优化，但滤波器的尺寸为0.149λg×0.574λg。上述的滤波器设计都各有各的优势和特点，但可以看出，滤波器的尺寸普遍偏大。本文通过增加U型微带谐振器设计了一款小型化的带阻滤波器。

1 带阻滤波器的仿真与分析

本文所设计的带阻滤波器结构如图1所示。

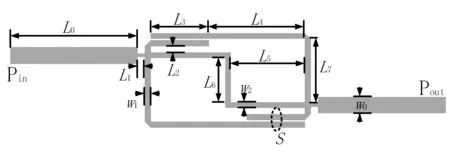
图1 滤波器结构示意图

该滤波器可以简单分解成两个结构，即中间的1/4波长传输线，以及两个相互耦合的U型微带谐振器，这两部分通过阶跃阻抗与输入端口、输出端口相连接。图1中，Pin和Pout为输入和输出端口，L0和w0分别为输入及输出传输线的长度和宽度，L1为阶跃阻抗传输线的长度，L2、L3、L4、L7为U型微带谐振器的枝节长度，L5、L6为1/4波长传输线的长度，w1和w2分别为U型谐振器和1/4波长传输线的宽度。

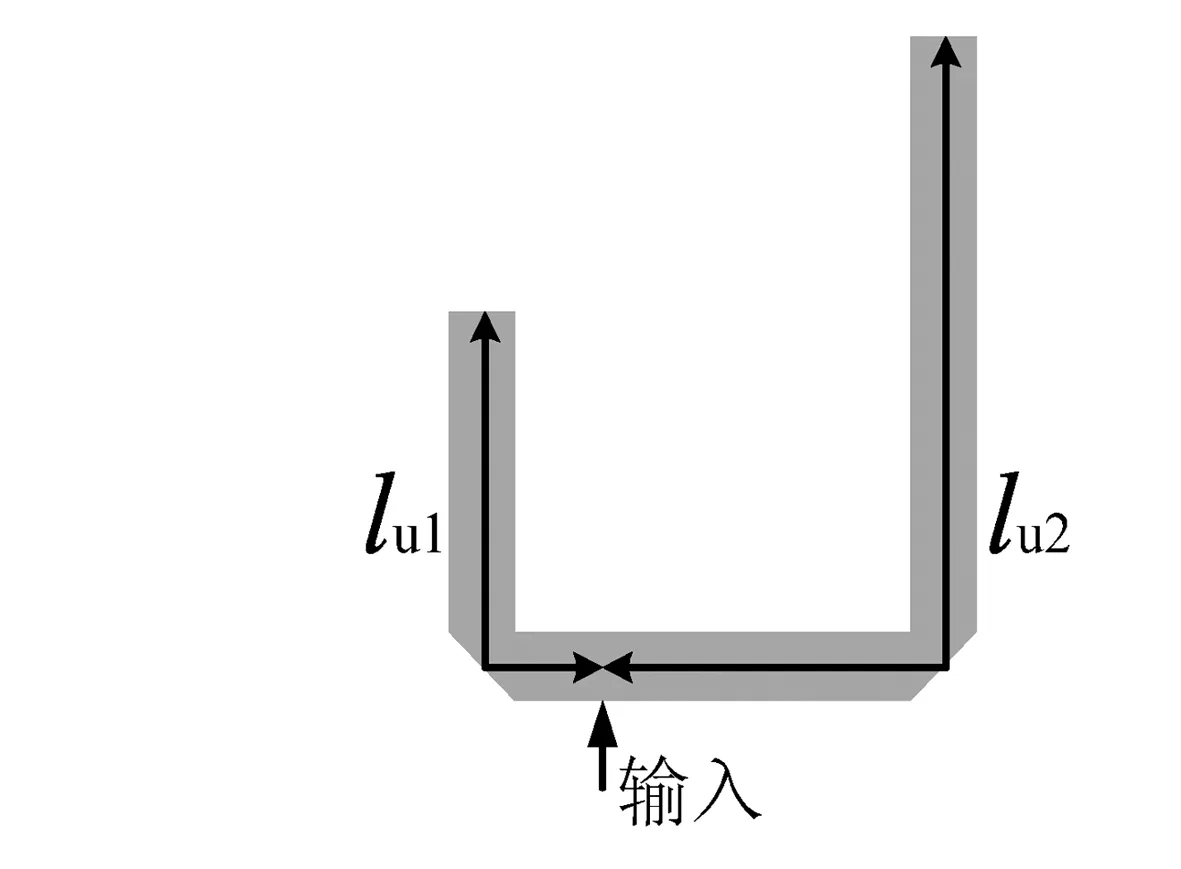
图2 U型谐振器的结构

为了讨论引入的U型谐振器对于滤波器性能的影响，本文先单独对U型谐振器进行分析，其结构如图2所示。

从图2中可看出，U型谐振器的两个枝节长度不一，分别记作lu1和lu2。U型谐振器通过对传输线的折叠，减小了滤波器的尺寸，实现了小型化的设计。

图3是增加U型谐振器前后滤波器的仿真结果对比。

从图3中可以看出，当仅有1/4波长传输线而没有U型谐振器时，滤波器几乎为全通滤波器，此时滤波器存在两个传输极点，分别位于0 GHz附近和5.55 GHz附近。当加入U型谐振器之后，带阻滤波器明显增加了2个传输极点和2个传输零点，分别在1.12、2.42、2.84和3.53 GHz附近。显然，这些传输零点和传输极点是由U型谐振器带来的，它们的存在优化了滤波器的滤波特性：两个传输零点相互靠近，形成了一个传输阻带，可以滤除不必要的噪音信号；而位于阻带左右两边的传输极点，则能优化滤波器过渡带的陡峭程度。

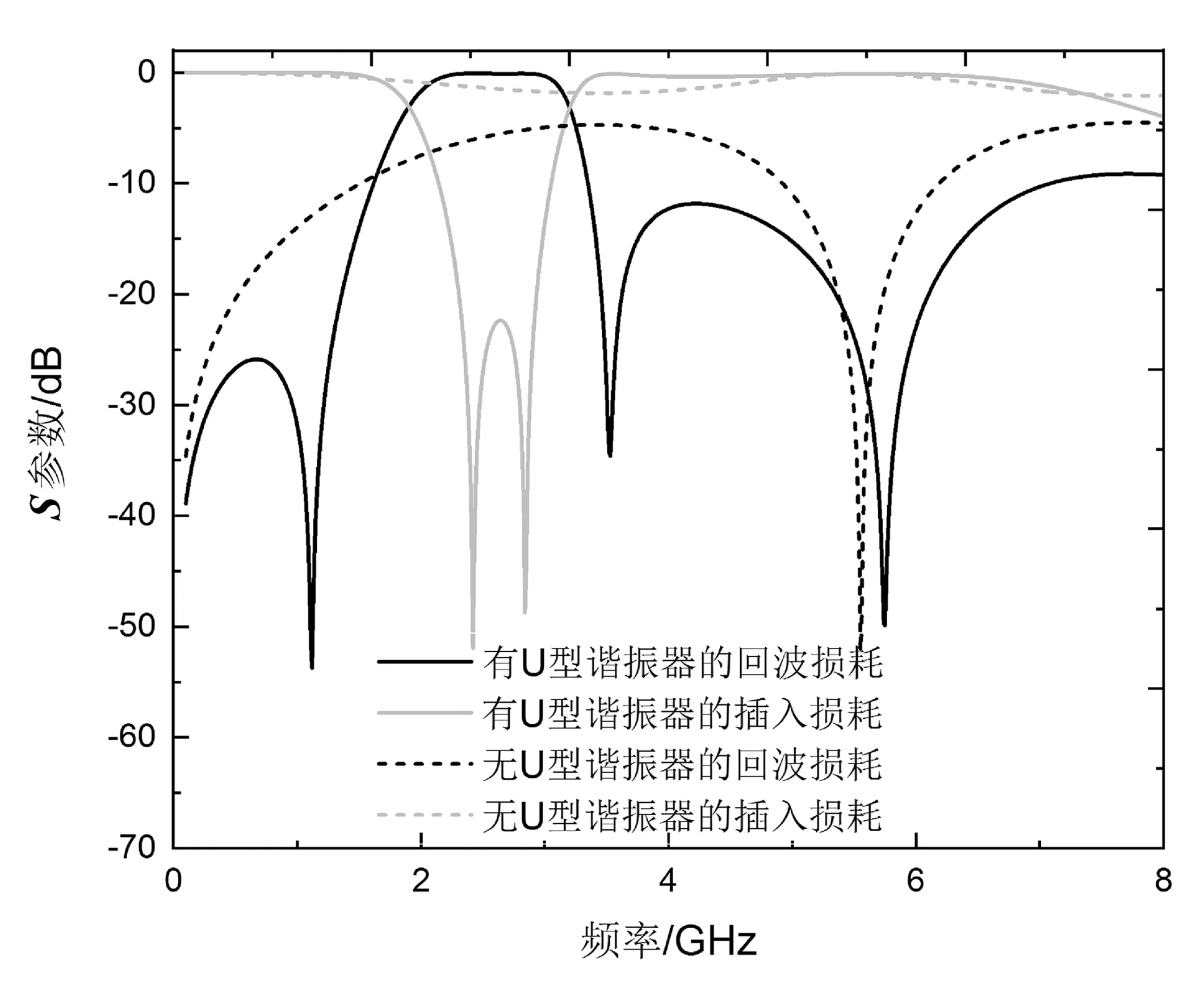
图3 有无U型谐振器的S参数仿真结果对比

1.1 U型谐振器的分析

U型谐振器一共会带来两个传输零点和两个传输极点。对于U型谐振器，根据滤波器的S参数公式可以得到其插入损耗。二端口网络的S参数矩阵与Y参数矩阵的转换公式为：

(1)

其中：Z0为U型谐振器的特征阻抗；β=2π/λg，而λg为电波在传输线上的传输波长；lu为U型谐振器的总长度，即lu=lu1+lu2，ω为角频率；Cs1为电磁耦合系数。

要求传输零点的频率，可以令S21=0，此时由式(1)转换得到：

(2)

该等式即为传输零点需要满足的条件。由于U型谐振器的电磁耦合系数Cs1很小，因此由式(2)可以得到：

cos (βlu1)cos (βlu2)=0

(3)

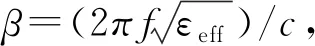
(4)

(5)

式(4)、(5)中，n为自然数，n=0,1,2,…。从式(4)、(5)中可看出，两个传输零点的频率会受到U型谐振器的两个枝节长度所影响，U型谐振器枝节长度越长，所对应的传输零点频率越小。同时，当式(4)和式(5)中的n取相同阶级时，fz1和fz2的数值会相互接近，可形成一个阻带。同理，令U型谐振器的回波损耗为零，根据二端口网络的S参数矩阵与Y参数矩阵的转换公式可得：

(6)

经计算可以得到，U型谐振器的传输极点应满足条件

cos (βlu1)cos (βlu2)=∞

(7)

由此可以得到U型谐振器的传输极点为：

(8)

(9)

显然，两个传输极点的频率也会受到U型谐振器的两个枝节长度所影响，U型谐振器枝节长度越长，所对应的传输极点频率越小。

综上所述，U型谐振器的两个枝节长度分别会影响滤波器的传输零点和传输极点的频率，调整合适的枝节长度即可以得到所需要的频率；反之，根据所需要的频率也可以计算出对应的U型谐振器枝节长度。因此，在设计带阻滤波器时，可以先根据中心频率推断出形成阻带的两个传输零点的值，再利用式(4)和式(5)计算出对应的U型枝节长度，最后根据传输极点对枝节长度进行调整，即可得到满足设计要求的滤波器。

1.2 滤波器的仿真分析

采用三维电磁软件高频结构仿真器(high frequency structure simulator, HFSS)对U型谐振器进行仿真，进一步分析U型谐振器对于带阻滤波器的传输零点和传输极点的影响，其仿真结果如图4所示。

从图4中可以看出，U型谐振器产生两个谐振零点和两个谐振极点，其中谐振极点fm1的频率最小，谐振极点fm2的频率最大，而两个谐振零点fz1和fz2的频率介于两个谐振极点之间形成阻带。U型谐振器的枝节长度L3、L4、L7对于滤波器的传输零点和传输极点都有影响。当L3、L4或L7的长度增加时，fz1、fz2、fm1和fm2的频率都会随之减小，带阻滤波器的中心频率也会随之减小，但带宽的变化不明显。另外，这几个参数对于滤波器性能的影响不是单一的，这是因为U型谐振器并不是简单的级联，而是通过谐振器的长枝节与短枝节耦合而串联起来。因此，在设计滤波器时，需要结合各个参数一同调整，才能获得最好的滤波器性能。

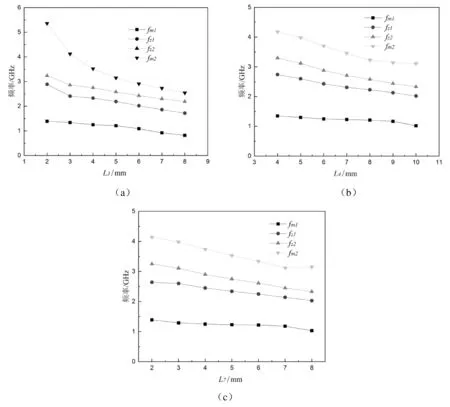
图4 U型谐振器各枝节长度对传输零点、传输极点的影响

总而言之，要设计带有U型结构的带阻滤波器，只需要根据设计要求的中心频率，确定所需要的传输零点和传输极点的频率，便可依据式(4)、(5)、(8)和(9)计算出合适的U型谐振器枝节长度，之后再对各个枝节的长度进行微调以调整带阻滤波器的性能。

2 滤波器的加工与测量

设计了一款中心频率为2.45 GHz的带阻滤波器。首先，根据设计的中心频率计算出1/4波长传输线的长度，即图1中的L5+L5+L6。其次，通过中心频率推断出传输零点和传输极点的频率，代入上文中的式(4)、(5)、(8)和(9)即可计算出U型结构的枝节长度，即图1中的L2+L3和L3+L4+L7。在得出各枝节的长度后，根据所设计的带阻滤波器的结构确认适合L2～L7的数值，并利用HFSS建模仿真。由于公式计算是在理想条件下建立的，所以在仿真过程中必须对滤波器及输入、输出传输线的参数进行微调以获取最佳的工作性能。

带阻滤波器的最终电路参数为：L0=8.2 mm、L1=0.47 mm、L2=0.4 mm，L3=4.36 mm、L4=7.0 mm、L5=5.47 mm、L6=3.1 mm、L7=4.52 mm、w0=1.36 mm、w1=0.53 mm、w2=0.38 mm、s=0.1 mm。带阻滤波器的实物图如图5所示。

图5 带阻滤波器的实物图

该滤波器加工使用的电路板介质材料是罗杰斯4350，厚度为0.508 mm，相对介电常数为3.48。滤波器位于介质板的正面，介质板背面是整片的金属地。

带阻滤波器的实物测试结果如图6所示。

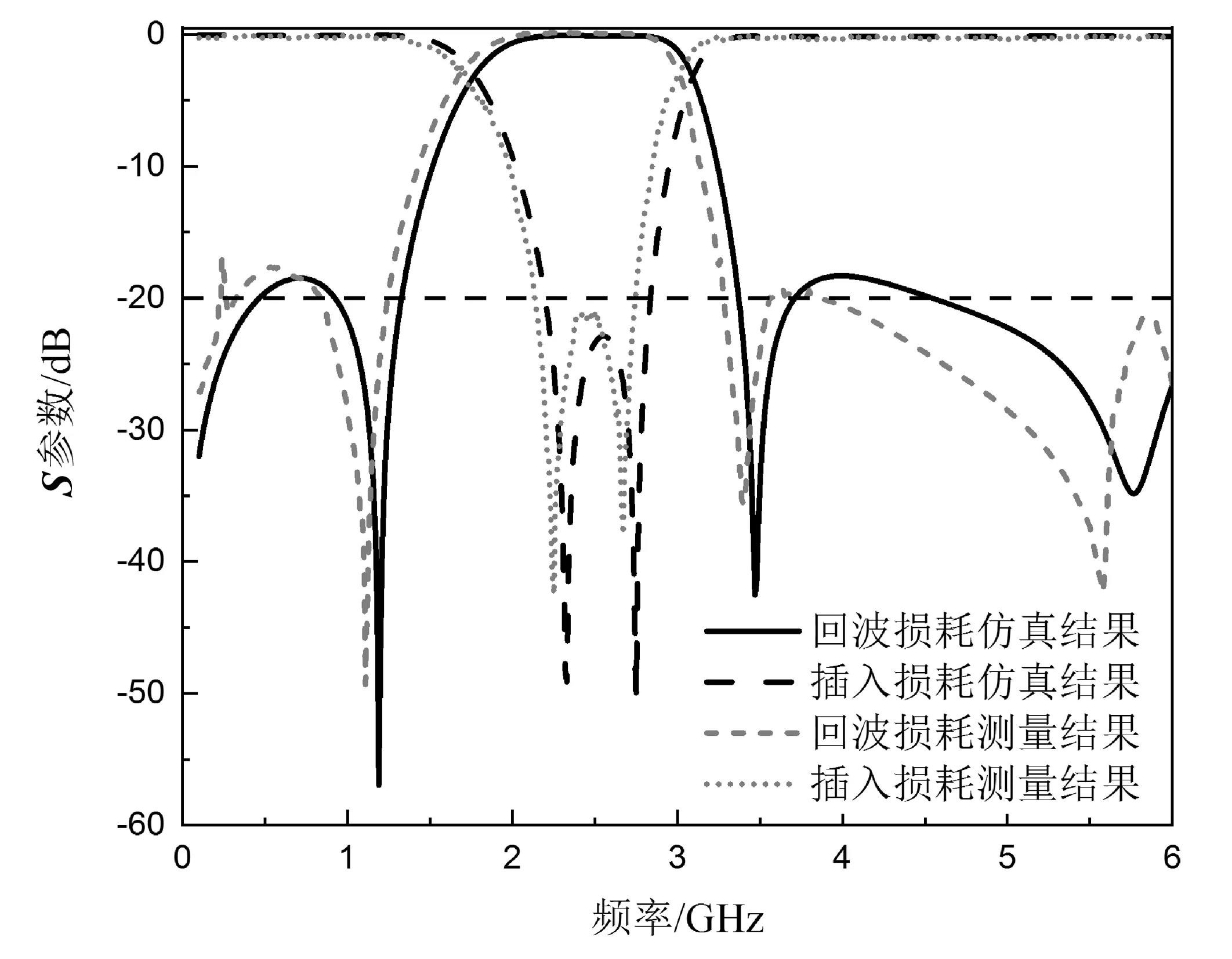
图6 滤波器的仿真与测试结果

根据测试结果可知，带阻滤波器实际测量的中心频率为2.44 GHz，20 dB带宽为0.62 GHz，两个零点分别位于2.67和2.65 GHz。滤波器的通带回波损耗大于17 dB，4个传输极点分别位于0、1.11、3.4和5.58 GHz。从图6可以看出，测量结果和仿真结果具有较好的一致性，两者之间的误差可能来源于加工误差、测量误差等。

表1为本文设计的带阻滤波器与已发表的文献中提出的带阻滤波器特点的比较。

从表1中可以看出，本文设计的滤波器相较于其他文献提出的滤波器具有较好的通带内回波损耗，且一个最明显的优势就是尺寸小于其他文献中提出的滤波器，实现了带阻滤波器的小型化设计。

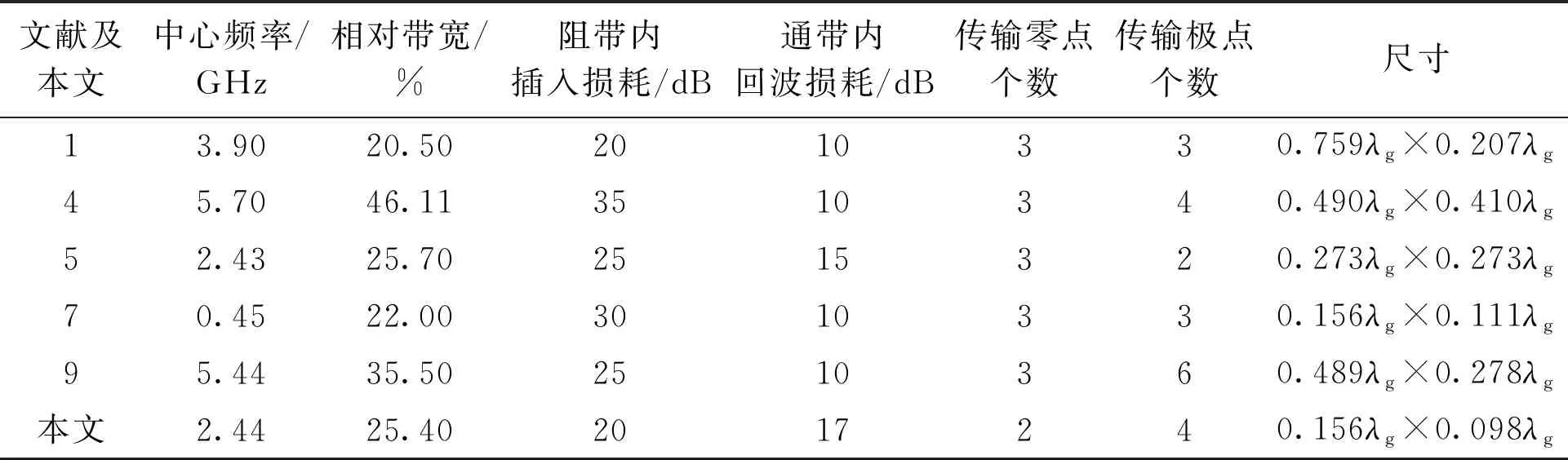
表1 本文滤波器与其他文献滤波器的比较

3 结 论

本文基于U型谐振器设计了一款结构简单、具有2个传输零点和4个传输极点的小型化微带带阻滤波器。通过对U型谐振器的分析，归纳出了U型谐振器的枝节长度对于其所带来的谐振零点、谐振极点的影响。因此，可以根据设计要求计算得到所需要的U型谐振器的枝节长度，从而设计出符合要求的带阻滤波器。最终设计的带阻滤波器使用厚度为0.508 mm、相对介电常数为3.48的介质材料进行加工，中心频率在2.44 GHz，测试结果和仿真结果较为一致，具有良好的工作性能，且滤波器的尺寸仅有0.156λg×0.098λg，实现了滤波器的小型化设计。