基于HJI的移动机器人轨迹跟踪控制

刘 鑫，陈昌忠，王 蓉，唐荣嘉

（1.四川轻化工大学自动化与信息工程学院，四川 宜宾 644000；2.人工智能四川省重点实验室，四川 宜宾 644000）

引 言

移动机器人由于其灵活性高和实用性强，现已广泛应用于工业领域和社会场所[1]。但是，由于其本身具有非完整约束、强非线性、强耦合性等不确定因素，要对其进行良好的控制具有一定困难。文献[2]对跟踪误差进行泰勒处理，利用Lyapunov 理论设计了具有局部渐进稳定的跟踪控制器。文献[3]采用动态线性化反馈，提出了具有指数收敛的全局跟踪控制器。虽然以上研究实现了轨迹跟踪，但是忽略了非线性因素的影响。文献[4]利用反演法设计了具有全局指数渐进稳定的跟踪控制器。针对传统滑模控制的缺点，文献[5]将全局稳定定理与指数趋近率相结合，文献[6]将模糊控制与滑模控制进行结合，文献[7]通过自适应技术与滑模控制相结合，均有效地减少了滑模抖振。文献[8]针对重复运动的移动机器人系统，提出了一种基于数据驱动的高阶迭代学习控制算法。文献[9]针对移动机器人左右轮驱动控制系统，把双输入双输出控制系统解耦成单输入单输出的控制系统，并对单输入单输出系统分别设计控制器。以上控制方法虽然都能够对移动机器人进行良好的轨迹跟踪控制，但是并未考虑移动机器人的动力学模型。文献[10]结合动力学模型提出了基于惯性检测单元的跟踪控制方法。在具有外部扰动的情况下，文献[11]设计了具有干扰观测器补偿的力矩控制器，文献[12]设计了一种直接模糊自适应输出反馈控制器，都取得了良好的跟踪效果。

本文针对动力学具有外部扰动的移动机器人运动学模型，采用反步法设计了辅助速度控制率；针对其动力学模型，基于哈密顿-雅可比不等式（Hamilton-Jacobi Inequality，HJI）设计了前馈控制和反馈控制相结合的控制方法，最后利用MATLAB将计算力矩控制与本文提出的控制方法进行数值仿真对比。

1 移动机器人运动学及其模型

考虑一类受非完整约束的三轮移动机器人，它有两个驱动轮和一个万向轮，如图1 所示。万向轮无动力装置，仅起支撑作用。两驱动轮轴距为2a，驱动轮半径为r，S为两驱动轮的轴心。XOY表示笛卡尔坐标系，X0SY0表示机器人坐标系，用向量q=[x y θ]T，V=[v ω]T来表示移动机器人的状态，[x y]表示移动机器人在笛卡尔坐标系中的位置，θ表示其运动方向与笛卡尔坐标系X轴正方向的夹角。v和ω分别表示移动机器人的线速度和角速度。

图1 移动机器人结构示意图

移动机器人在纯滚动、无滑动条件下的非完整约束[13]为：

将其改写成如下形式：

选择一满秩转换矩阵S(q)，满足

通过矩阵S(q)把机器人坐标系下的速度V转换为笛卡尔坐标系下的速度q̇，即

则移动机器人的运动学方程为：

移动机器人动力学方程[14]通常可以表示为：

其 中：M(q)∈R3×3为 系 统 正 定 惯 性 矩 阵；C(q,q̇ )∈R3×3为 与 位 置 和 速 度 有 关 的 矩 阵；G(q)∈R3×1为重力矩阵；F(q̇ )∈R3×1为摩擦力项；τd∈R3×1为有界的未知扰动；B(q)∈R3×2为输入变换矩阵；τ∈R2×1为控制力矩；A(q)为约束矩阵；λ为约束力。

对式（4）进行求导得：

将式（4）和式（7）代入移动机器人的动力学方程式（6），左乘ST( )q，整理后得：

其中：

假设机器人在水平面上运动，且不考虑摩擦因素。即G(q)= 0，F(q̇ )= 0，则式（8）可写为：

式（10）为变形后的移动机器人一阶动力学模型，根据文献[16]，可知其具有以下性质：

性质1：对于任意的q，参数矩阵( )q为对称矩阵。

2 哈密顿-雅可比不等式理论

在模有界条件下，非线性不确定奇异系统的鲁棒可镇定性与一个扩展的HJI理论微分不等式存在正解等价[17]。本文基于HJI 来设计动力学反馈控制器，并用HJI 理论证明动力学系统的稳定性。假设一非线性系统如下：

其中：d为外界干扰，z为系统的评判指标。

为了评判系统的抗干扰能力，定义如下性能指标：

其中J为系统的L2增益，它与系统的鲁棒性负相关。J越小，系统的鲁棒性能越好。

根据文献[18]，HJI 理论描述为：对任意给定一个正数γ，如果存在一个正定且可微的函数L(x)≥0，并且

则J≤γ。

3 控制器设计

为了实现移动机器人对参考轨迹的跟踪，设计如下控制方案：

（1）为了实现移动机器人运动学位置跟踪，基于反步法设计运动学辅助速度控制器。

（2）为了实现移动机器人动力学速度跟踪，基于HJI设计动力学前馈控制器和反馈控制器。

3.1 运动学控制器设计

假设移动机器人在笛卡尔坐标系中的参考位姿为qr=[xr yr θr]T，根据参考机器人和移动机器人在笛卡尔坐标系中的位置关系，可以得到位姿跟踪误差：

其中：ex为移动机器人坐标系X0方向的偏差；ey为移动机器人坐标系Y0方向的偏差；eθ为移动机器人转向角的偏差。

对式（14）求导，得跟踪误差变化率为：

其中：vr≥0、ωr≥0 分别为给定的线速度和角速度。参照文献[19-20]，采用反步法设计辅助速度控制率为：

其中：β1、β2、β3均为大于零的可调节的控制器参数。

3.2 动力学控制器设计

定义速度跟踪误差：

根据式（10），设计前馈控制率为：

其中u为反馈控制率。

将式（18）代入式（10）得动力学误差模型：

设动力学系统的评判指标z=ec，则式（19）可写为：

为了保证动力学控制系统的稳定，基于HJI 理论设计反馈控制器为：

根据以上分析，设计出移动机器人的控制结构如图2所示。

图2 移动机器人运动学和动力学系统控制结构图

4 系统稳定性

定义移动机器人运动学系统和动力学系统的Lyapunov函数分别为L1和L2：

显然，L1≥0，L2≥0。只有当e1、e2、e3都为0 时，L1= 0；当ec= 0时，L2= 0。

对L1求导，结合式（14）～（15）可得：

显然，L̇1≤0。

对L2进行求导，可得：

结合式（19）可得：

定义

将式（26）代入式（27）可得：

结合式（27）可知：

由HJI 理论可知，动力学系统的L2增益J≤γ，结合式（12）可知‖ ‖z满足性能指标，即速度跟踪误差ec收敛，动力学系统稳定，且γ越小，误差ec越小，系统的鲁棒性越好。

5 仿真验证

采用MATLAB 软件，以图1所示的机器人为例，运动学控制系统采用相同的控制器，且动力学控制系统采用计算力矩控制法与本文所设计的控制方法进行对比仿真实验。

移动机器人的质量m为10 kg，转动惯量I为5 kg·m2，轴距2a为0.40 m，驱动轮半径r为0.05 m，设参考轨迹为圆心在原点、半径为2 m 的圆，参考速度vr= 1 m/s，ωr= 0.5 rad/s。参考机器人的初始位姿为qr0=[2 0 π/2]T，受控移动机器人的初始位姿为q0=[1 0.5 π/6]T。选择辅助速度控制器参数β1= 4.0、β2= 6.0、β3= 5.5，根据文献[21]，采用计算力矩控制法设计力矩控制器为:

其中kp为2 × 2的参数矩阵，选取kp=。选取本文所设计的力矩控制器参数γ= 0.06。仿真时，设外界不确定干扰为采样时间（0.02 s）的随机高斯白噪声，如图3所示。

图3 外界白噪声干扰曲线

图4(a)所示为移动机器人在两种方法下的轨迹跟踪仿真曲线图，图4(b)所示为两种方法下的位姿跟踪误差曲线图。由图4 可知，传统的计算力矩控制下的移动机器人在5 s以后逐渐跟踪上参考轨迹，但是轨迹跟踪误差始终不能收敛到0，存在抖动。而在本文方法下的移动机器人在2 s 以后便能够逐渐跟踪上参考轨迹，并且轨迹跟踪误差几乎为0。这说明本文所设计的控制方法控制性能好，系统具有良好的抗扰性。

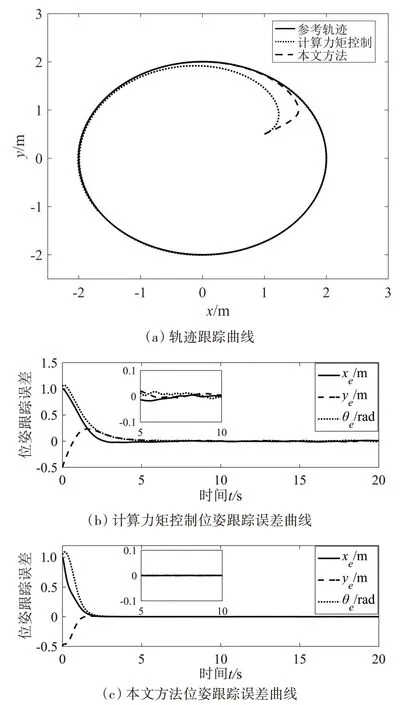
图4 不同方法下轨迹跟踪仿真与位姿跟踪误差曲线

图5所示为采用计算力矩控制法和采用本文控制方法时，移动机器人动力学系统实际速度输出对辅助速度控制输入的跟踪曲线图。由图5(a)可知，计算力矩控制下的移动机器人的线速度和角速度在将近5 s时跟踪上运动学辅助速度输入，跟踪效果较差；而图5(b)中本文方法下的移动机器人的线速度和角速度在0.5 s以内就能跟踪上运动学辅助速度输入，跟踪效果良好。图6 所示为两种方法的速度跟踪误差图。由图6 可以看出，采用本文的控制方法时，移动机器人速度跟踪误差的收敛速度很快，能够在0.5 s之前迅速收敛到几乎为0。而采用计算力矩控制时移动机器人的速度跟踪误差在5 s 左右收敛，且收敛误差始终在0 附近来回抖动。根据仿真的结果可知，计算力矩控制由于抗干扰能力弱，在面对外界干扰时，移动机器人的跟踪性能差。而本文基于HJI理论所设计前馈控制加反馈控制的方法，在面对外界干扰时，移动机器人能够在极短的时间内实现速度的完美跟踪，且误差几乎无抖动。这说明本文所设计的动力学控制方法具有良好的跟踪性能，控制系统具有良好的抗扰性。

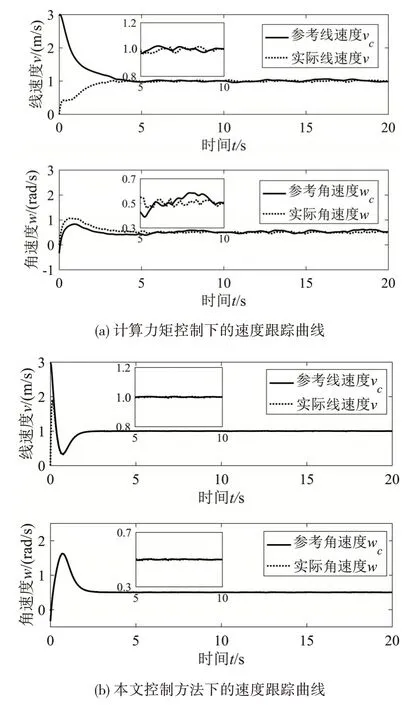
图5 不同方法下速度跟踪曲线

图6 速度跟踪误差曲线

图7 所示为本文方法下的力矩控制器输出的左、右力矩曲线图。由图7 可知，移动机器人左、右轮控制力矩输出均在2 s之后逐渐稳定。

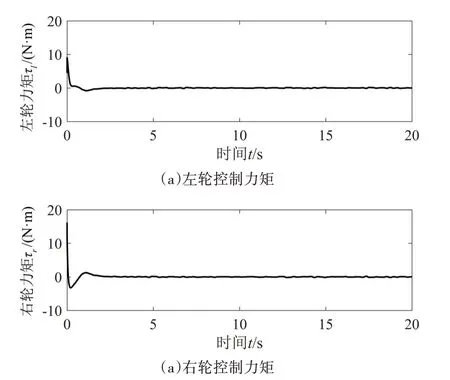
图7 左右轮控制力矩曲线

6 结束语

通过考虑一类受外界干扰的非完整移动机器人，针对其运动学模型基于反步法设计了运动学控制器。针对其动力学模型设计了前馈控制器，并把动力学误差模型转换为HJI 所需的非线性模型，在此基础上设计了反馈控制器。该控制方法设计简单，需调节的参数少。仿真结果证明本文所提出的控制方法是有效的，在具有外部不确定干扰的情况下，移动机器人能够快速、准确、稳定地跟踪上参考轨迹，控制系统具有良好的抗扰性。