基于随机差分进化算法的最优PID参数整定方法

杨茂华，谭 飞,2，尹宋麟

（1.四川轻化工大学自动化与信息工程学院，四川 宜宾 644000;2.人工智能四川省重点实验室，四川 宜宾 644000）

引 言

PID 控制由于其控制适应性能好，有较强的鲁棒性，算法结构简单，成为工业中最常见的一种控制技术，广泛用于各大控制行业中[1]。同时根据不同工况的要求，也对PID 进行了一系列改进。国内外学者在PID 控制参数整定方面进行了深入研究，目前已有很多种PID参数整定方法。文献[2]采用了模糊控制的方式对控制参数进行整定，用超前控制与迭代PID 型学习律相结合的方法有效地提高了控制的精准度，改善了控制的效果。文献[3]选取一阶时延系统进行研究，总共引用了6 种PID 整定技术并分析了它们的性能。文献[4]设计了一种递阶预测控制优化算法，基于时间分解，将优化时域长度增加所引起的大规模参数优化问题分解成独立的小规模参数优化问题，得出显式优化解，并通过Matlab 仿真验证，取得了较优的控制效果。文献[5]将改进动态变异差分进化（DMDE）算法用于最优PID 控制中，通过灵敏度分析，提高了系统稳定性，缩短了响应时间。文献[6]介绍了一种基于PID的最优控制策略，采用改进版的爬山算法和Firefly算法，在性能和鲁棒性方面进行了4种控制器之间的比较分析，并通过仿真证明了即使存在干扰的情况下，仍能保持良好性能。文献[7]将一种预测自动耦合PID（PAC-PID）控制算法应用于设计烟草温度和水分含量的控制，并通过仿真结果表明，该方法能够平滑、快速、高精度地跟踪目标信号。文献[8]提出了一种离散时间的分数阶PID 控制，通过在真实的三阶单输入单输出系统上进行评估，将分数阶PID与经典整数阶PID 进行比较，得到了更好的最终响应。模糊控制及神经元控制近些年发展成果不断。引入模糊和神经元这两种模块对控制器进行改进，使控制系统具备学习功能，此类控制器不依赖于具体的模型因而鲁棒性很强[9]。邢鹏飞[10]将神经网络与继电振荡法相结合，研制出了一种新型的PID 调节器。汤赵建等[11]将内模PID 控制应用到多变量时滞系统并取得了良好的性能。李瑶瑶[12]将模糊控制与内模控制相结合开展研究，并将研究结果用到高压共轨柴油机进行仿真，最终取得了较好的成果。

本文针对一阶时滞系统和三阶系统，提出了一种基于随机差分进化算法（SDE）的PID 参数整定方法，通过大量数据的拟合计算，最终得出一个PID 参数整定公式，该公式能够大大提高参数整定效率，并且整定效果良好。其中的随机差分进化算法（SDE），将原有差分进化算法进行改进，不仅保证了差分算法种群多样性，还能确保收敛速度快。

1 PID参数整定

1.1 PID参数整定方法

PID 控制器作为一种线性控制器，将给定值与实际值的差构成偏差，再将偏差的比例（P）、积分（I）和微分（D）通过线性组合构成控制量来对受控对象进行控制，最终转变为对Kp、Ki、Kd3 个参数的调节。其中：Kp为比例系数；Ki=Kp/Ti，为积分系数；Kd=Kp×Td，为微分系数。而Ti为积分时间常数，Td为微分时间常数。

目前主流的PID 参数整定方法有5 种：第一种是经验法，这种方法需要工程技术人员了解控制对象和控制系统的工作机理和工作情况，该方法较粗糙，具有随机性；第二种是等幅振荡法，通过观察振幅进行调参，先调Kp，取较小值，观察到等幅振荡后，再根据周期和控制类型调节Ki和Kd；第三种是衰减系数法，先调节积分环节，将积分时间放大，微分环节调为0，调节Kp使波动情况达到4∶1 衰减，再根据控制规律进行调节；第四种是响应曲线法，也是较普遍的方法，手动状态下，改变控制器的Kp、Ki、Kd，记录被控对象的响应曲线，可参考Ziegler-Nichols 参数整定方法的计算公式进行调参，最终获得较好的响应曲线，记录Kp、Ki、Kd；最后一种便是通过智能算法，如遗传算法[13-14]、差分进化算法[15-16]、神经网络[17]等进行PID 参数整定，该方法整定效果最好，具有稳定性和快速性，是目前最有效的PID 参数整定方法。本文采用的PID 参数整定便是基于随机差分进化算法（SDE）的PID 参数整定，通过随机产生的Kp、Ki、Kd，将时间与误差绝对值乘积积分（ITAE）性能指标作为目标函数，不断优化迭代进化，找到最优的控制PID 参数。其差分进化算法进行PID参数整定的流程图如图1所示。

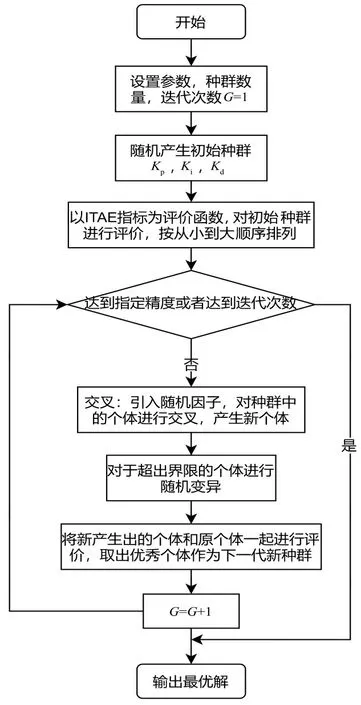
图1 差分算法PID参数整定流程图

1.2 随机差分进化算法

与传统差分算法不同，随机差分算法引入随机因子，产生一个种群维度的0～1 列向量替换缩放因子，使种群多样性得以提升，避免因种群趋同陷入局部最优解的情况，同时交叉方式选用适应度好的精英个体进行交叉，有效地加快了种群的收敛速度。

2 PID参数整定方法

2.1 内模控制原理

若对系统采用普通闭环的PID 控制，其PID 控制的系统框图如图2 所示。其中，Gc(s)为控制器的传递函数，G(s)为被控对象，E(s)为偏差，R(s)为输入，Y(s)为输出，s为复频率。

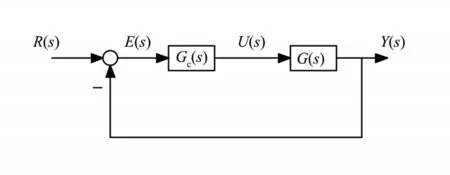
图2 普通闭环控制图

而内模控制（Internal Model Control，简称IMC）和普通闭环控制不同，内模控制的控制器的输出不仅输出到控制对象，也输出到模型内部，反馈环节为系统的实际输出值和内部模型的输出值之差。内模控制的结构如图3 所示，其主要特点便是具有很高的鲁棒性和很强的抗干扰能力。图3 中，GIMC为内模控制器，D(s)为干扰信号，、̂分别为对应的估计值，C代表控制模块，U为控制输入模块。

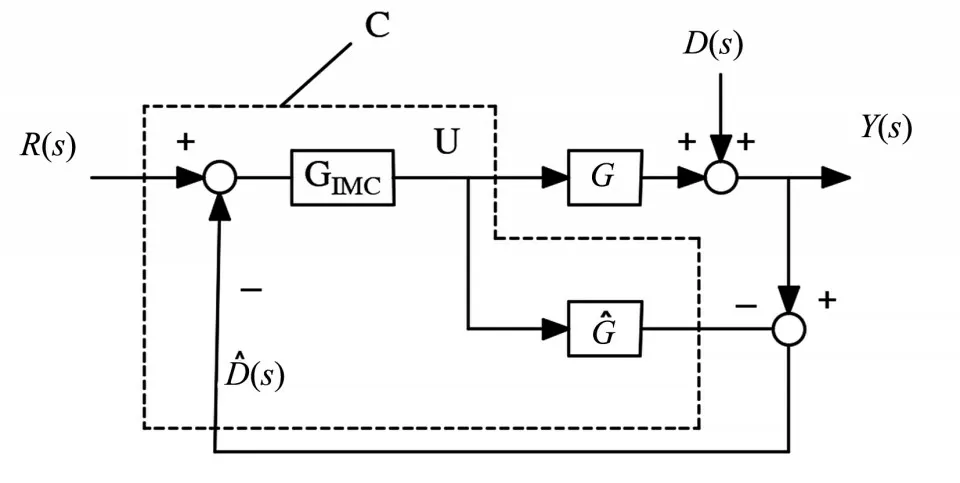
图3 内模控制结构图

2.2 基于内模控制的PID控制器

由于绝大部分的传递函数皆可用一阶时滞模型来代替（对于高阶模型，可通过一阶时滞模型进行降阶），所以，本文以三阶模型为例，将一阶时滞模型进行整定方法提取。

当过程模型为三阶模型，则有：

式中K、A、B、C为三阶模型传统函数参数。通过模型转换，可将其近似为一阶时滞模型：

再将纯滞后模型通过一阶Pade逼近：

式中Km、Tm、τ为一阶时滞模型参数，则采用一阶滤波器得到内模控制器的传递函数为：

式中λ为时间常数。

对于三阶系统来说，基于内模控制器原理所得的最优PID参数整定方法为[18]：

2.3 一阶时滞系统最优PID参数方法

考虑到文献[18]中的参数不是最优参数，现将式(5)～(7)进行一般化处理，提取出一种新的针对三阶系统的PID 参数整定公式。通过对一阶时滞系统的参数整定规律可知，一阶时滞系统参数整定跟τ与Tm的比值，即时滞大小的参数[19]有关，所以对式(5)～(7)进行以下变换。

将式(5)分母提出Km，得式(8)：

将式(8)进行一般化处理，引入未知参数α和β，得式(9)：

将式(6)左右同时除以τ得式(10)：

将式(10)进行一般化处理，得式(11)：

将式(7)化简为式(12)：

对式(12)右边分子分母同时除以τ，得式(13)：

将式(13)进行一般化处理，引入未知参数μ,得式(14)：

最终得到PID 参数整定方法公式为式(9)、(11)、(14)。

根据文献[4]，ITAE指标较其他误差指标具有快速、稳定性好的优点，所以选用ITAE 指标进行参数整定。经过多次高阶系统降阶为一阶时滞系统的程序运行结果统计，发现大部分高阶系统近似为一阶时滞模型后的参数中的τ在0.5～1 之间，Tm在1～2之间，故选用表1 中参数，采用差分进化算法进行PID参数整定。

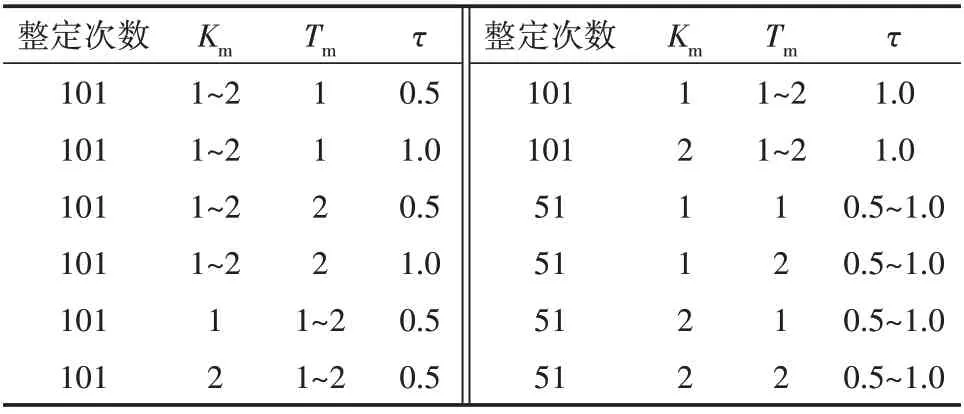
表1 寻优的最优PID的各参数及其评价指标值列表

通过基于差分优化算法及ITAE 最优1000 多次的PID 参数整定，得到大量的数据，将数据用Matlab的Curve Fitting工具箱进行函数拟合，最后得到了一系列未知系数优化值分别为：

通过工具箱拟合的图像如图4（已删掉误差大的点）所示。

图4 公式拟合图

图4 中，X、Y分别为和，X1、Y1 分别为和，Z为。

从图4 可以看出采集点和设定曲线拟合度较高，说明了该公式模型的正确性。将以上参数代入式(9)、(11)、(14)便可得到针对一阶时滞系统最优的PID参数方法：

最终便得出以上基于差分进化算法对三阶系统和一阶时滞系统最优PID参数方法的研究结果。

3 仿真实验验证

3.1 高阶模型降阶

取文献[18]中的三阶系统被控对象：

通过随机差分进化算法进行低阶等效，获得一阶时滞模型：

Matlab 程序运行结果如图5～7 所示。对比文献[18]，可以看出本文的近似模型与实际模型拟合度更高，偏差和适应度更小。

图5 阶跃响应偏差图

图6 适应度变化图

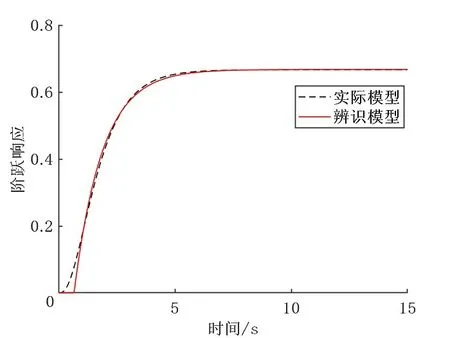
图7 辨识模型输出与实际输出对比图

3.2 公式法和差分算法整定对比

通过PID参数整定公式方法计算得：

采用差分算法PID参数整定的结果为：

采用文献[18]内模PID参数整定的结果为：

阶跃响应信号曲线如图8 所示，从图中可以看出，前两种PID 参数整定结果存在差异，但整定方法得出的曲线达到了稳定，且控制效果较好，均没有超调量，说明了该整定公式的可行性。

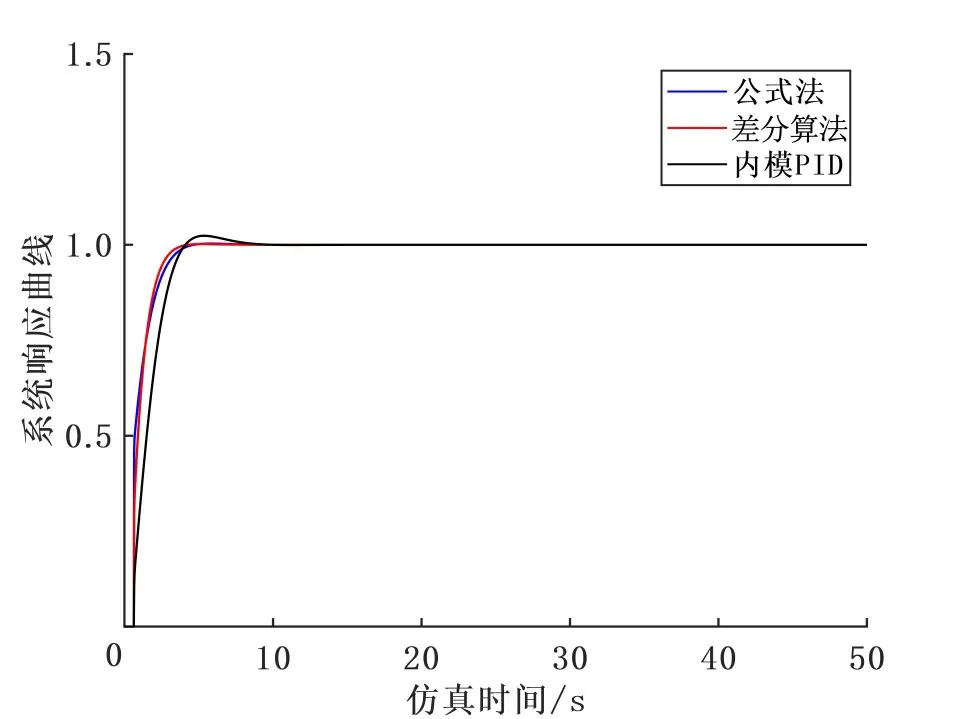
图8 响应曲线对比图

3.3 PID参数方法评估

通过随机差分算法进行PID 参数整定，最终得出一个基于一阶时滞系统的PID 参数整定公式。该公式能快速计算出PID 各参数的值，且不需要手动调整和估计控制参数的初始值。

4 结束语

通过智能优化算法中的差分进化算法，首先将高阶系统近似为一阶时滞系统，并以ITAE作为评价函数对一阶时滞进行PID 参数整定，得到最优PID参数；其次将得到的PID 参数进行函数拟合，得到一个PID 参数整定公式；最后将公式得到的PID 参数结果进行对比，通过Matlab 仿真实验验证了该公式的有效性和可行性。