Two-level optimization approach to tree-level forest planning

Yusen Sun ,Xingji Jin,＊ ,Timo Pukkl,b,＊＊ ,Fengri Li

a Key Laboratory of Sustainable Forest Ecosystem Management -Ministry of Education,School of Forestry,Northeast Forestry University,Harbin,150040,Heilongjiang,China

b University of Eastern Finland,P.O.Box 111,80101,Joensuu,Finland

Keywords:Differential evolution Heuristic-optimization Individual-tree detection Multi-objective optimization Simulated annealing

ABSTRACT Background: Laser scanning and individual-tree detection are used increasingly in forest inventories.As a consequence,methods that optimize forest management at the level of individual trees will be gradually developed and adopted.Results: The current study proposed a hierarchical two-level optimization method for tree-level planning where the cutting years are optimized at the higher level.The lower-level optimization allocates the trees to the cutting events in an optimal way.The higher-level optimization employed differential evolution whereas the lower-level problem was solved with the simulated annealing metaheuristic.The method was demonstrated with a 30 m ×30 m sample plot of planted Larix olgensis.The baseline case maximized the net present value as the only management objective.The solution suggested heavy thinning from above and a rotation length of 62 years.The baseline problem was enhanced to mixed stands where species diversity was used as another management objective.The method was also demonstrated in a problem that considered the complexity of stand structure,in addition to net present value.The objective variables that were used to measure complexity were the Shannon index (species diversity),Gini index (tree size diversity),and the index of Clark and Evans,which was used to describe the spatial distribution of trees.The article also presents a method to include natural advance regeneration in the optimization problem and optimize the parameters of simulated annealing simultaneously with the cutting years.Conclusions:The study showed that optimization approaches developed for forest-level planning can be adapted to problems where treatment prescriptions are required for individual trees.

1.Background

Increased use of laser scanning has made it possible to detect individual trees in forest inventories(Vauhkonen et al.,2011;Contreras and Chung,2013;Wing et al.,2019).The laser scanning data include the locations and intensities of the return pulses of laser beams.These data may be processed into a canopy height model,which typically is a raster showing the canopy height in small raster cells.The local maxima of the canopy height model show the approximate locations of the trees,which can be found more accurately from the original return pulse data(point cloud).The perimeters of tree crowns can be interpreted by using segmentation methods (Pascual,2021a,b),and the tree diameter can be predicted with allometric models,using tree height and crown area as predictors(Packalen et al.,2020;Pascual,2021a,b).If the tree species is unknown,it may be predicted using auxiliary data (for instance digital aerial photos),or the point cloud data and advanced interpretation methods(Vauhkonen,2010).

It seems likely that forest inventories will increasingly produce treelevel data.A logical consequential aim is to use these data in forest management planning(Wing et al.,2019;Packalen et al.,2020;Pascual,2021a,b),which calls for the development and adoption of new forest planning approaches.There are already several studies on methodologies that optimize forest management at the tree level (Pukkala and Miina,1998;Contreras and Chung,2013;Fransson et al.,2019).Two research lines can be seen in these studies.The first line is to optimize a tree selection rule,which helps to identify trees that should be removed in a thinning treatment(Pukkala and Miina,1998;Pukkala et al.,2015).The parameters of these rules can be optimized simultaneously with the cutting years.For example,Pukkala et al.(2015) used a rule where the decision to remove a tree depended on the stumpage value and relative value increment of the tree,and the effect of removing the tree on the growth of remaining trees.The idea was to find trees that are financially mature for cutting (low relative value increment),give much income(high stumpage values) and,if removed,would enhance the growth of the remaining trees.

The other research line seeks to optimize the removal decision separately for each tree(Contreras and Chung,2013;Wing et al.,2019;Fransson et al.,2019;Packalen et al.,2020;Pascual,2021a,b).In this approach,the decision space(number of possible decisions)is very large and the number of optimized variables is much higher than in the decision rule approach.If several cuttings are optimized,the number of possible combinations of tree-level decisions is huge even in a small stand.For example,if the stand has 100 trees and the length of the period during which an individual tree may be cut is 80 years,the number of different combinations of tree removals is 80100=2.04 × 10190.The studies conducted so far omit or mitigate this problem by optimizing only one thinning treatment(e.g.Contreras et al.,2013;Packalen et al.,2020;Pascual,2021a)or reducing the number of possible cutting years(Wing et al.,2019;Fransson et al.,2019;Pascual,2021b).

The latter approach to tree-level planning is comparable to those methods of modern forest planning that are based on tree stands.The basic difference is that the decision unit is a tree instead of a stand.Therefore,the same optimization methods that are used in stand-based forest planning can be used directly when cutting prescriptions are optimized for trees.The correspondence with stand-level planning is especially clear in those tree-level planning cases where the stand is divided into Voronoi polygons (also called Thiessen polygons),one for each tree.This partitioning of the growing space can be seen as a“stand”delineation where each stand has only one tree (Packalen et al.,2020).The same non-spatial or spatial optimization methods that are being used in stand-based forest planning can be used directly in the tree-level approach.For example,Packalen et al.(2020) used a cellular automaton to select the harvested trees and to aggregate or disperse them.The spatial distribution of harvested trees was affected by minimizing or maximizing the common border between the Voronoi polygons of harvested trees.The cellular automaton and the same approach to spatial optimization (maximizing or minimizing the common border of simultaneously harvested adjacent stands) have been used earlier in stand-based forest planning(Heinonen and Pukkala,2007).

Correspondingly,Fransson et al.(2019)used the genetic algorithm to select the optimal combination of cutting years for individual trees.Genetic algorithm has been used frequently also in such forest planning where the prescriptions are optimized for stands (e.g.,Bettinger et al.,2002).Other metaheuristics that could be used to optimize tree selection include simulated annealing,threshold accepting,great deluge,tabu search,and ant colony optimization(e.g.,Bettinger et al.,2002;Jin et al.,2016).Linear programming and integer programming can also be used to derive treatment descriptions either for stands or trees and to aggregate or disaggregate harvested stands or trees(Pascual,2021a,b).

Metaheuristics have been used successfully with very large decision spaces (Heinonen et al.,2018).For example,Pukkala (2019) used a cellular automaton in a spatial forest planning problem that included 140,000 calculation units (raster cells),and the non-spatial planning problem of Pukkala (2020) included nearly 50,000 stands with altogether almost two million alternative treatment schedules for 100 years.These experiences suggest that the existing methodologies could be used without any major problems also in such forest planning cases where the prescriptions are developed for individual trees.However,there is an important difference in the planning process when the prescription unit is a stand vs.a tree.In the former case,the planning process typically includes two steps (Kangas et al.,2015).First,alternative treatment schedules are simulated for the stands.Second,the optimal combination of the simulated schedules is found by using mathematical programming or metaheuristics.The two-step approach assumes that the development of a single stand does not depend on adjacent stands,which is a valid enough assumption in most cases.

In tree-level planning,however,it cannot be assumed that the development of an individual tree is independent of adjacent trees.As a consequence,all combinations of the cutting years of trees that are inspected during optimization must be simulated.This greatly increases the computing time compared to the two-step case.Therefore,the computational burden of tree-level planning is much higher although the planning problem may not be more complicated or larger than those that are based on forest stands.

This study developed and tested a hierarchical two-level optimization approach for mitigating the problem of the excessively high computational burden of long-term tree-level planning.In this approach,the cutting years are optimized at a higher level,and the allocation of trees to different cuttings is optimized at the lower level.This approach greatly reduces the number of possible combinations of tree-level decisions.For example,in the case of 100 trees and 3 cuttings during a rotation,the number of the combinations of tree-level decisions is 3100=5.15×1047in the two-level approach,whereas there would be 80100=2.04×10190combinations (3.95 × 10142times more) in the one-level approach if trees can be harvested during 80 years.

The article first describes the approach outlined above and then provides single-objective and multi-objective optimization examples.The optimizations were conducted for a larch plantation(Larix olgensis)located in the Heilongjiang Province of north-eastern China.

2.Methods

2.1.Outline of the method

The principle of the method is to optimize the cutting intervals at a higher level and the selection of removed trees at a lower level(Fig.1).The higher-level optimization tests several combinations of cutting years.Each combination of cutting years is passed to a lower-level optimization,which finds the optimal cutting event for every tree of the stand.All assignments of trees to the cutting events that are tested in the lowerlevel optimization are simulated.This simulation calculates the net present value,harvest removals,and other possible objective variables.The values of the management objectives are passed back to the higherlevel algorithm,which gets feedback on the worth of the cutting years when the trees are assigned optimally to the cutting events.The higherlevel optimization then makes changes in the cutting years according to the principles of the algorithm and the same process is repeated.

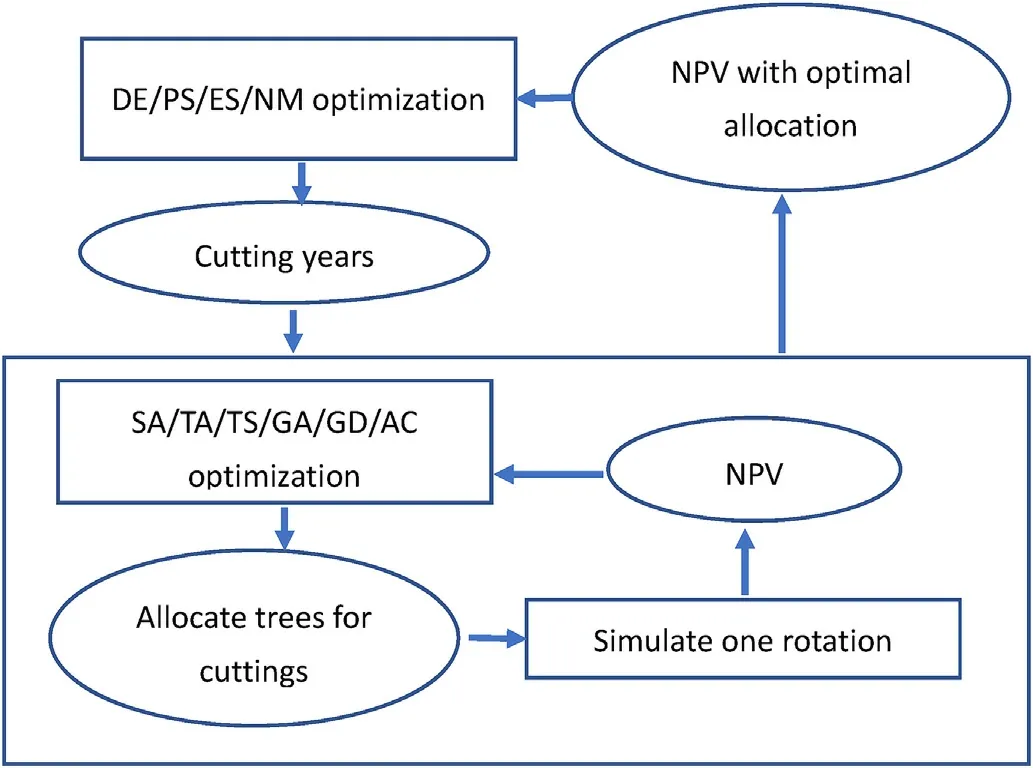
Fig.1.The layout of the two-level optimization method developed and demonstrated in this study.The methods that can be used to optimize cutting years include differential evolution (DE),particle swarm optimization (PS),evolution strategy optimization(ES)and the method of Nelder and Mead(NM).The metaheuristics that can be used to assign trees to different cutting events include simulated annealing (SA),threshold accepting (TA),tabu search (TS),genetic algorithm (GA),great deluge (GD) and ant colony optimization (AC).

2.2.Optimization methods

The variables that are optimized at the higher level(cutting intervals or cutting years)are continuous(real numbers)whereas integer variables are optimized at the lower level.The lower level problem is a typical combinatorial problem seeking the best combination of cuttings for individual trees.Therefore,the optimization algorithms that are the most suitable for the higher and lower levels are not the same.Fig.1 lists a few alternative methods that can be used at the two levels.All methods mentioned in Fig.1 have already been used in forestry planning,and there are studies on their performance (Bettinger et al.,2002;Pukkala and Heinonen,2006;Pukkala,2009;Arias-Rodil et al.,2015;Jin et al.,2016,2018).These studies show that differential evolution might be a good choice for the higher level,and simulated annealing has consistently performed well in combinatorial forest planning problems.Therefore,these two methods (differential evolution and simulated annealing)were used in the case study problems of this article,although all the methods of Fig.1 were programmed in the software that was used in this study.

Differential evolution is a population-based method for non-linear optimization (Storn and Price,1997;Pukkala,2009).It operates with several sets of decision variables(solution vectors).In the current study,the decision variables were cutting intervals (years to the first cutting,years from the first to the second cutting,etc.).The number of solution vectors was equal to ten times the number of optimized cutting intervals(e.g.,30 solution vectors with three cuttings during the rotation).The initial solution vectors were generated by drawing the cutting intervals randomly from the uniform distribution.The ranges were 0-30 for the first interval (years from the start to the first cutting) and 5-30 for the other cuttings (years from previous cutting).The allocation of trees to different cuttings was optimized for each solution vector to obtain the objective function values for the initial solutions.

After producing and evaluating the initial solutions the algorithm tries to improve each of them for several iterations.In this process,the values of the elements of the solution vectors are either maintained or taken from a so-called noise vector that is produced from three solution vectors as follows:

whereyiis elementiof the noise vector,xAi,xBiand xCiare the values of the same element in three,randomly selected solution vectors and λ is a parameter(0.5 used in this study).One randomly selected solution vector was replaced by the noise vector with certainty.For the other vectors,each element was replaced by the noise vector value with a probability of 0.5.This produced a modified candidate solution,in which some of the cutting intervals may the same as before and some other intervals may be different.The value of the modified solution vector (set of cutting intervals) was evaluated in the same way as the initial vectors.If the modification improved the solution,it was accepted,and otherwise,it was rejected.The process of modifying and evaluating the solution vectors was repeated for several iterations(30 in this study).The solution of the differential evolution algorithm is the best member of the population of solution vectors at the end of the last iteration.

The parameters of differential evolution are population size,i.e.,number of solution vectors(30 in this study),probability of drawing the element from the noise vector (0.5),parameter λ of Equation (1) (0.5),and number of iterations (30).The parameter values were based partly on the study of Jin et al.(2018)and partly on preliminary analyses where the aim was to find a compromise between computing time and quality of the optimization result.

The lower-level optimization algorithm was simulated annealing,which operates with one solution vector.The solution vector consisted of the cutting events of different trees(the values were 1,2,or 3 when there were three cuttings during the rotation).The initial solution was produced by assigning the cutting event randomly for each tree.The management schedule,consisting of the cutting intervals and the cutting events of trees,was simulated,and the simulation calculated the net present values and other possible objective variables for the schedule(examples given later).

Then,a random tree was selected and its cutting event was changed randomly.This kind of small change in the solution is called a move.The move produced a new candidate solution,which was evaluated by simulating the slightly different management schedule.The move was accepted if it improved the objective function value (for instance net present value).Otherwise,the move was accepted with the following probability(Jin et al.,2016):

whereOFCurrentis the objective function value of the solution before implementing the move,OFCandidateis the objective function value after the move,andTis“temperature”,which determines the probability of accepting inferior moves.The temperature was decreased toward the end of the search,which decreased the probability of accepting inferior moves.The search was stopped when the temperature reached a“freezing temperature”,which is one of the parameters of the method.The parameters of simulated annealing are starting temperature,cooling rate,freezing temperature,and search intensity.The cooling rate is a multiplier that produces the next temperature (next temperature=cooling rate × current temperature).Search intensity is the number of candidates(moves)that are produced at each temperature.In the current study,the cooling rate was 0.9,the freezing temperature was 0.001 times the initial temperature,and the search intensity was 0.3 times the number of trees in the plot.Previous studies (Pukkala and Heinonen,2006;Jin et al.,2018) show that the starting temperature should be of the same magnitude as the effect of a move on the objective function value.In this study,the starting temperature was set as follows

whereTStartis the starting temperature,OFis an estimate of a typical value of the objective function(based e.g.on preliminary optimizations),andNis the number of trees within the plot.

2.3.Case study data and models

The case study optimizations were conducted for larch(Larix olgensisA.Henry) plantations in the Heilongjiang Province of northeast China.One sample plot was randomly selected from the dataset that was used for growth modeling in the recent study of Dong et al.(2021).The size of the selected plot was 30 m by 30 m,and the age of the plantation was 22 years.No commercial cuttings had been conducted in the plot before the measurement.

The individual-tree models of Dong et al.(2021) for tree height,diameter increment,and survival were used to simulate the stand development under each of the management schedules that were evaluated during the optimization run.The assortment volumes of the removed trees were calculated with the taper models of Peng et al.(2018).The assortments into which the harvested stems were partitioned were:large log (minimum length 4 m,minimum top diameter 22 cm),medium log(4 m,18 cm),small log(4 m,12 cm),and pole(4 m,6 cm).The stumpage prices of these assortments were 1,100,950,800,and 600 RMB•m-3,respectively (one RMB was equal to 0.14 €or 0.16 USD in November 2021).These are the same assortment definitions and timber prices as used in Peng et al.(2018)except that a large log was taken as an additional assortment.

In simulations,the last cutting was clear-felling and the other cuttings were thinning treatments.In the examples of this study,the number of cuttings was three (two thinnings and clear felling).Earlier literature recommends using two or three thinning treatments before the final felling inLarix olgensisplantations(Peng et al.,2018).

The harvest incomes were discounted to the beginning of the rotation and summed.In addition,the stand establishment and tending costs at the beginning of the rotation were taken into account when calculating the net present value (NPV)of the simulated rotation.These costs were the same as in Peng et al.(2018):7000 RMB•ha-1in year zero,and 1500 RMB•ha-1in year 10.The NPV of the simulated rotation was converted to the NPV of an infinite sequence of similar rotations.NPV was calculated with a 3%discount rate.

The model for tree survival gives the probability that the tree survives for one year.A common way to apply this type of model in tree-level simulation is to compare the survival probability to a uniformly distributed random number [0,1] and assign the tree as a survivor if the random number is smaller than the survival probability.However,in optimization calculations,repeated runs with the same decision variables should preferably give the same value for the objective function,which means that stochastic simulation should be avoided.Therefore,the uniform random numbers,to which the survival probability was compared,were generated for each tree at the beginning of the optimization run.Consequently,repeated simulations with the same decision variables were identical.

3.Planning cases

3.1.Baseline run

The baseline run maximized the NPV with a 3%discount rate as the only management objective.The optimal thinning years were 30 and 57,and the optimal clear-felling year was 62 (Fig.2).Both thinnings removed mainly large trees,which means that the thinnings were from above.There was some mortality before the first thinning (Fig.2,top right) but very little mortality thereafter.The NPV of the optimized management schedule was 187,179 RMB•ha-1.

Fig.2.Tree map of the sample plot at the beginning of the simulation(top left),first thinning(top right),second thinning(bottom left),and final fellin（g bottom right)when NPV is maximized.The remaining live trees are indicated with green color,trees that are removed in a particular cutting with red color,trees removed in earlier cuttings with open circles,and dead trees with grey color.The diameter of the circle is proportional to the dbh of the tree.G=stand basal area,D=quadratic mean diameter.(For interpretation of the references to color in this figure legend,the reader is referred to the Web version of this article.)

The thinnings were heavy.The first thinning reduced the basal area from 31 to 9.9 m2•ha-1and the second from 32.8 to 8.8 m2•ha-1(Fig.2).The removed volume of the second thinning was higher than the clear-felling volume (Fig.3).The results suggest that optimal cuttings always remove all or almost all trees that give large and medium-sized logs,and all smaller trees should be left to continue growing.It seems that the years and intensities of cuttings mainly depend on the time points when a significant portion of trees reaches financial maturity and give large and medium-sized logs.This means that the optimal cutting years might be quite different for different stands.

3.2.Enhancement 1:Mixed stand

The method used above to maximize the NPV works also in mixed stands without any modifications.The models for simulating stand dynamics and calculating assortment volumes need to be available for all species present in the stand or plot.However,mixed stands may have management objectives concerning the species mixture.One such objective is species diversity,which can be described with the index of Shannon and Weaver(Shannon,1948).The index(henceforth referred to as Shannon index)is calculated as

wherenis the number of species present in the stand or plot,andpiis the proportion of speciesi(of the number of trees,stand basal area,stem volume,etc).In this study,the proportions of different species were calculated from their basal areas.To demonstrate the use of species diversity as a management objective,a part of the trees of the plot were assumed to be different species that survives better but grows slower thanLarix olgensis.The following utility function was maximized instead of NPV:

wherewiis the weight anduiis the sub-utility function of management objectiveiandSis the mean Shannon index of the rotation.The mean was calculated from the Shannon index values at the beginning,before and after each thinning treatment,and before the final felling.The subutility functions were linear,and they converted the values of the objective variables to range 0-1 as follows:

when the objective variable is maximized,and

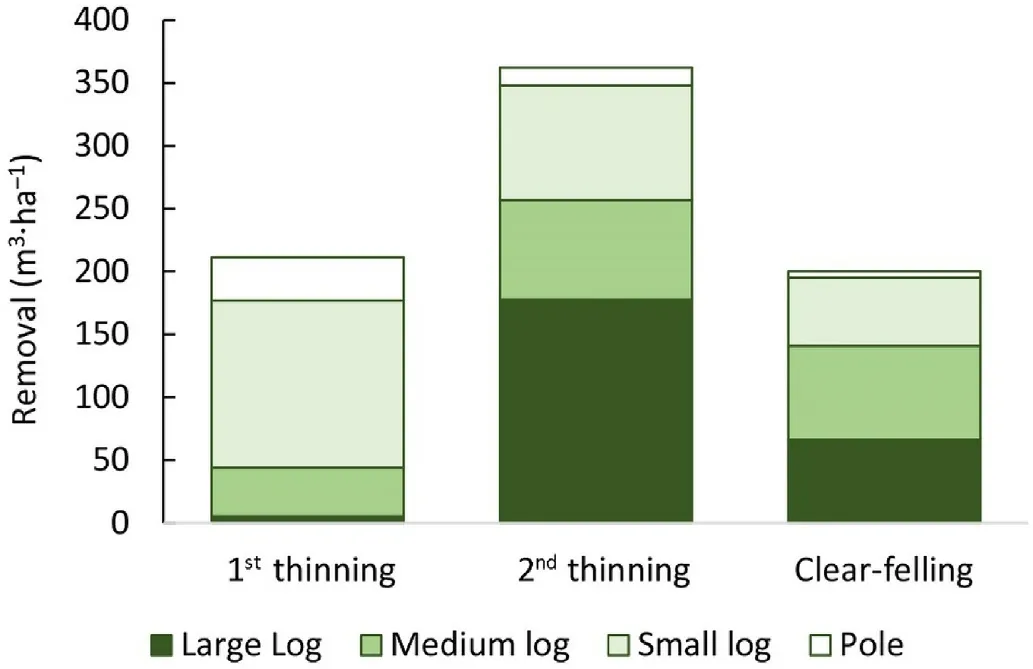
Fig.3.Removed volumes of different assortments when the net present value was maximized with a 3% discount rate.

when the objective variable is minimized.In Equations(6) and (7),qis the achieved amount of the objective variable,andqminandqmaxare,respectively its lowest and highest possible values.If the theoretical minimum and maximum are unknown,they can be found by using singleobjective optimization.In this study,the maximum NPV was obtained from the baseline run and the maximum Shannon index was calculated to be 0.693 for a mixture of two species (n=2).The minimum values of both objective variables were assumed to be zero.The weights of both objective variables(w1andw2in Equation(5)) were 0.5.

When the Shannon index was maximized simultaneously with the NPV,it was optimal to conduct the thinnings in such a way that the postthinning basal areas of both species were equal (Fig.4).When the Shannon index was minimized and NPV was maximized,the first thinning removed all trees of the secondary species with the consequence that the Shannon index decreased to zero (Fig.5).These results can be taken as proof that the optimization found the optimal tree selection in terms of the Shannon index since the optimizations produced solutions that are known to be optimal in terms of species diversity.

3.3.Enhancement 2:Managing the forest for complexity

Tree plantations are often monotonic monocultures where all diversity is minimal.It has been suggested that forest management should aim at more complex stand structures,which would increase the diversity and resilience of the forest(Thompson et al.,2009;Messier et al.,2019).To demonstrate the optimization of forest management for increased complexity,two additional objective variables were added to the utility function,namely the Gini index(Gini,1921)and the index of Clark and Evans (1954).The use of the Gini index has been recommended for describing the variability of tree size(Valbuena et al.,2012).The index of Clark and Evans describes the regularity of the spatial distribution of trees.

The Gini index was calculated as described in Valbuena et al.(2012).The trees were sorted into ascending order according to their diameter at breast height(dbh),after which the rate of basal area accumulation was calculated as a function of the accumulation rate of the number of trees resulting in the Lorenz curve (Valbuena et al.,2012).If both variables accumulate with the same rate,all trees are of equal size leading to a Gini index equal to zero and a straight Lorenz curve(the black line in Fig.6).If most of the stand basal area is concentrated in a few trees,the value of the Gini index is high,which indicates high size diversity(red line in Fig.6).The theoretical maximum of the Gini index is one.

The aggregation index of Clark and Evans(R) is

Calculation of the average distance from a tree to its nearest neighbor needs information on the surroundings of the plot.In this study,a temporary 5-m-wide buffer zone was generated around the plot by assuming that the plot is surrounded by similar plots on all sides.The buffer zone was removed immediately after calculating the Clark and Evans index.

The management of the mixed plot(the same plot as in the previous example) was optimized by either minimizing or maximizing the complexity of the stand structure,together with the maximization of the NPV.The utility function was

Fig.4.Tree map of the sample plot of a mixed stand at the first and second cutting when Shannon index is maximized (left) or minimized (right) and NPV is maximized.Remaining live trees are indicated with green (Larix olgensis) and blue (secondary species) color,trees that are removed in a particular cutting with red color (secondary species with darker tone),trees removed in earlier cuttings with open circles,and dead trees with grey color (all dead trees are Larix olgensis).The diameter of the circle is proportional to the dbh of the tree.(For interpretation of the references to color in this figure legend,the reader is referred to the Web version of this article.)

whereGis the Gini index.When complexity was maximized,S(species diversity) andG(size diversity) were maximized andRwas minimized(spatial aggregation was maximized).The sub-utility functions forGandRwere similar to Equations(6)and(7).All the weights(wi)of Equation(9) were 0.25.

Maximization of complexity led to management where a mixture of the two species was maintained in both cuttings (dashed red line in Figs.5 and 8).The thinning treatments removed both large and small trees,maintaining the Gini index at a reasonably high level(Fig.7,Fig.8 top).The spatial distribution of trees was converted towards a very aggregated spatial pattern,which can be seen from the lower-left map of Fig.7,and the decreasing value Clark and Evans index(red dashed line in Fig.8).

The stand development was quite different when the complexity was minimized (and NPV was maximized).The spatial distribution of trees developed toward a systematic pattern (Fig.8,bottom right),and the value of the Clark and Evans index increased (Fig.8).All trees of the secondary species were removed in the first cutting (Fig.7,top right),and the value of the Gini index decreased during the rotation,implying decreased size diversity(Fig.8).

The NPV of the management schedule was 150,722 RMB•ha-1when complexity was maximized and 174,628 RMB•ha-1when complexity was minimized.Therefore,aiming at a complex stand structure decreased economic profitability.This was most probably mainly because some large trees were left to continue growing beyond their economic maturity for cutting,and the admixture of the secondary tree species was kept high,although the growth rate of the secondary species was lower than that of the primary species(Larix olgensis).

3.4.Enhancement 3:Ingrowth

Fig.5.Development of the Shannon index when NPV is maximized while maximizing (max Shannon) or minimizing (min Shannon) species diversity.“max Complexity”is a case where NPV,Shannon index,and Gini index are maximized and the index of Clark and Evans is minimized.In the“min Complexity”case,NPV and the index of Clark and Evans are maximized,and Shannon and Gini indices are minimized.

Fig.6.Lorenz curves between basal area and number of trees for three plots.If all trees have the same diameter,the basal area and the number of trees accumulate at equal rates,resulting in a straight Lorenz curve and a Gini index equal to zero(black line).If most of the basal area is in a few trees,the Lorenz curve of very curvilinear and the Gini index is high (red line).(For interpretation of the references to color in this figure legend,the reader is referred to the Web version of this article.)

The optimization cases discussed so far represent rather simple forest structures and management systems because natural regeneration was ruled out.The optimization examples shown above apply only to evenaged rotation forestry where the possible advance regeneration(ingrowth) is ignored in forest management.However,earlier studies(e.g.,Pukkala et al.,2014)show that in cases where a planted forest gets natural advance regeneration,it may be optimal to let the advance regeneration develop,and gradually remove the planted trees.This makes it possible to postpone the next tree planting and the associated costs.Promoting advance regeneration also helps to create more complex and resilient forest structures.

Our next optimization example includes ingrowth.It is assumed that seedlings of a shade-tolerant species gradually appear in the stand.The number of ingrowth trees decreases with increasing basal area.The ingrowth trees are assumed to have a higher survival rate under severe competition but a lower growth rate,as compared toLarix olgensis.

Technically,the possibility of ingrowth was implemented in the optimization by using a tree list longer than the number of trees in the initial stand.Those places on the tree list that were not filled by the initial trees were empty (Fig.9).If new ingrowth trees appeared in the plot during a simulation,they occupied the empty places of the tree list.

The lower level combinatorial optimization algorithm (simulated annealing in our example) found the optimal cutting for all trees of the tree list(born and unborn).However,only those trees that were born at the moment of cutting contributed to harvest incomes and the indices that were used to describe species diversity,size diversity,and spatial aggregation.The same principle was also used to deal with mortality(Fig.9).If a tree died before its cutting year,it was ignored in the calculation of harvest removals and the index values of that year.

An optimization result where the optimal cutting year of an ingrowth tree is earlier than the year in which the tree appears to the plot means that the optimal management does not make use of the ingrowth tree.If the cutting years of ingrowth trees are later than the years of their appearance,the ingrowth trees may positively contribute to the management objectives.If there is mortality before the cuttings,it means that it is more optimal to let some trees die rather than thin the stand before the onset of self-thinning(see Fig.2,top right).

The rationale behind the tree list method described above is the fact that the management schedule is simulated after generating a candidate solution,i.e.,after assigning cutting years to the trees.Therefore,when trees are allocated to different cuttings,it is not known whether the tree will die before its cutting year,or whether the tree is born by the time of the cutting.

Two optimizations were conducted with the assumption of ingrowth.The first maximized the NPV and Gini index (with equal weights),and the second maximized NPV but minimized the Gini index.The tree list was two times longer than the initial number of trees in the plot.The ingrowth trees were placed in random locations (Fig.10) although in reality most of them might appear in canopy gaps and other places where the competition by existing trees is low(Pukkala et al.,2015).Since the locations of ingrowth trees are unknown,it is not reasonable to use the spatial index of Clark and Evans as an objective variable.

The maps of Fig.10 (left panel) show that larger trees were maintained in thinning when the Gini index was maximized.The NPV of the optimized schedule was 153,417 RMB•ha-1when the Gini index was maximized and 180,948 RMB•ha-1when the Gini index was minimized.The obvious reason for the lower NPV of the former schedule was that large financially mature trees were left unharvested when the Gini index was maximized.The average Gini index of the rotation was 0.401 when it was maximized,and 0.200 when it was minimized(while simultaneously maximizing NPV).

3.5.Enhancement 4:Optimizing the metaheuristic simultaneously with cutting years

The performance of a heuristic search method depends on its parameters,which for simulated annealing are starting temperature,freezing temperature,cooling rate,and the number of candidates produced and evaluated per temperature (search intensity).All these parameters can be optimized as shown in previous research (Pukkala and Heinonen,2006;Jin et al.,2016).The two-level planning approach suggested in this article can optimize the parameters of the metaheuristic simultaneously with the cutting years.

Previous studies show that the optimal parameter values of simulated annealing imply a slow cooling rate,low freezing temperature,and high search intensity,which would lead to very long computing times (Pukkala and Heinonen,2006).Therefore,studies that optimize the parameters of simulated annealing have used a time constraint,which sets the maximum time that can be used for the search(Jin et al.,2016).

In this study,we optimized only the starting temperature of simulated annealing with a fixed cooling rate (0.9) and search intensity (the number of candidates produced per temperature was 30%of the number of trees in the initial plot).The freezing temperature was always 0.001 times the initial temperature.Optimization was used to find a suitable starting temperature for the simulated annealing algorithm given that the other parameters are fixed or dependent on the starting temperature.The starting temperature is difficult to set,but it may have a significant influence on the efficiency of the algorithm.A too high starting temperature leads to a search process where all or most candidates (good and bad)are accepted at the beginning of the search,which means a waste of time.A too low starting temperature leads to runs where inferior solutions are never or seldom accepted,which increases the likelihood that the algorithm gets trapped in a local optimum.

Fig.7.Tree map of the sample plot of a mixed stand at the first and third cutting when complexity is maximized (left) or minimized (right) and NPV is maximized.Remaining live trees are indicated with green (Larix olgensis) and blue (secondary species) color,trees that are removed in a particular cutting with red color (secondary species with darker tone),trees removed in earlier cuttings with open circles,and dead trees with grey color(all dead trees are Larix olgensis).The diameter of the circle is proportional to the dbh of the tree.(For interpretation of the references to color in this figure legend,the reader is referred to the Web version of this article.)

The possibility to optimize the metaheuristic was demonstrated in the same plot that was used in the baseline run.The problem was the same,except that the starting temperature was optimized simultaneously with the cutting intervals.More exactly,the optimized variable was the multiplier of the following formula (see Pukkala and Heinonen,2006),which gives the starting temperature as a function of the magnitude of the objective function value(OF)and number of trees(N)

The optimization resulted in a multiplier value of 1.737,which is slightly lower than the value(2.0)used in the other optimizations of this article.The NPV of the optimized management schedule was 194,455 RMB•ha-1when the starting temperature was optimized whereas the NPV of the baseline run was 187,170 RMB•ha-1.The improvement in NPV was 3.9% when the starting temperature was optimized simultaneously with the cutting intervals.However,the management schedule was essentially similar to the baseline run(Fig.11).In both schedules,it was optimal to conduct heavy thinnings from above,where the trees that produced large and medium-sized trees were removed.The rotation length was 9 years longer(71 years instead of 62 years)when the starting temperature was optimized.In other respects,however,the management was very similar in both cases.

4.Discussion

The motivation behind this study was a vision of a new forest planning methodology,which is based on laser scanning data,individual-tree detection,and tree-level optimization.This methodology may consist of the following steps:

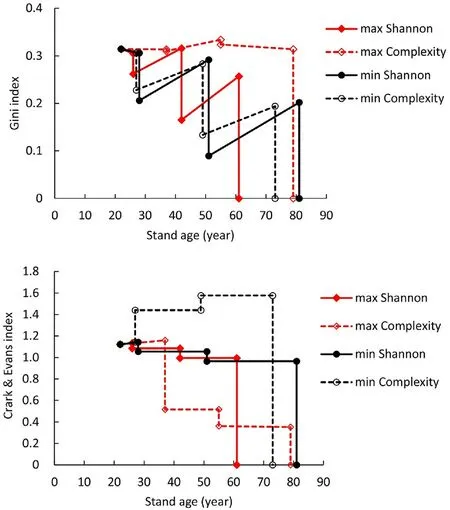
Fig.8.Development of Gini index (top) and the index of Clark and Evans(bottom) when NPV is maximized while maximizing (max Shannon) or minimizing (min Shannon) species diversity or maximizing (max Complexity) or minimizing (min Complexity) complexity.Maximizing complexity is equal to maximizing Shannon and Gini indices and minimizing the index of Clark and Evans.A low value of Clark and Evans indicates aggregated spatial distribution of trees.

(1) Laser scanning data are used to calculate the canopy height and other variables for raster cells

(2) The rasters of canopy height and other variables are used to automatically segment the forest into homogeneous stands (Jia et al.,2020;Sun et al.,2021)

(3) Individual trees are detected from the laser scanning data,separately for each stand(Vauhkonen et al.,2011)

(4) The method described in this study is used to optimize the cutting year of each tree

There are methodologies already for steps 1-3(Hyypp¨a et al.,2008;Wulder et al.,2008;Koch et al.,2009;Vauhkonen et al.,2014).The current and a few earlier studies show that Step 4 is also possible (Contreras and Chung,2013;Fransson et al.,2019;Wing et al.,2019).Our study demonstrated that methods that already exist and are in regular use can be successfully applied when the decision unit is a tree instead of a stand.The methodologies discussed in this article are the easiest in plantation forests but,as shown in this article,they can also be implemented in more complicated stand structures and silvicultural systems that rely on natural regeneration and aim at multi-layered multi-species stands.Spatial questions can be addressed by using aggregation indices like in this study,or aggregating or dispersing cut trees using methods developed in earlier studies(e.g.,Packalen et al.,2020).

However,it might be asked whether the approach discussed in this article is the most appropriate in all cases such as continuous cover forestry where the number of trees might be high and the locations of ingrowth trees are unknown.Instead of using the approach of the current study,it might make more sense to use the rule-based approaches described in earlier literature (Pukkala and Miina,1998;Pukkala et al.,2015).These approaches optimize a rule that is used to select the trees that are removed in a particular cutting.

The situation is the same in laser scanning inventories where only a part of the trees can be detected individually.Histogram matching and other methods can be used to predict the amount and size of those trees that are not detected from laser scanning data(Xu et al.,2014).However,the locations of trees that belong to the predicted or recovered part of the diameter distribution are unknown.If the proportion of non-detected trees is high,it might be more recommendable to use the rule-based approach to tree selection instead of the tree-level optimization discussed in this study.A further possibility is a hybrid method where tree-level optimization is used in the first cutting or for large trees,and a tree selection rule is used for small trees and later cuttings.

Forest planning problems may have objectives that make the optimal management schedules of different stands dependent on each other.Examples of these objectives are the cutting targets specified for the whole forest.Fortunately,there exist methods that make it possible to consider forest-level objectives and constraints while optimizing the management of individual stands.One of these methods is based on the concept of reduced costs and the dual prices of forest level constraints,which was first described by Hogason and Rose(1984)and later applied to spatial forest planning problems by Pukkala et al.(2008).The dual prices of the forest-level constraints depend on the difference between the realized values of the constraining variables and their target values in such a way that the absolute value of the dual price increases with increasing deviation from the target value.The use of the reduced cost approach requires that the optimization of the management schedules of stands is repeated several times and the dual prices are updated after every round based on the deviations of the constraining variables from their target values.This makes the method computationally demanding.

Fig.9.An example of the tree list used in optimizations where ingrowth is possible.The upper part of the diagram shows the status of each tree at the moment of cuttings(dead,living,not yet born,removed earlier)and the trees that are removed in different cuttings.The lower part is a summary showing trees that are never removed because they die before the cutting year(grey),are removed in cuttings (yellow),or are not removed because the tree is born after its cutting year (brown).(For interpretation of the references to color in this figure legend,the reader is referred to the Web version of this article.)

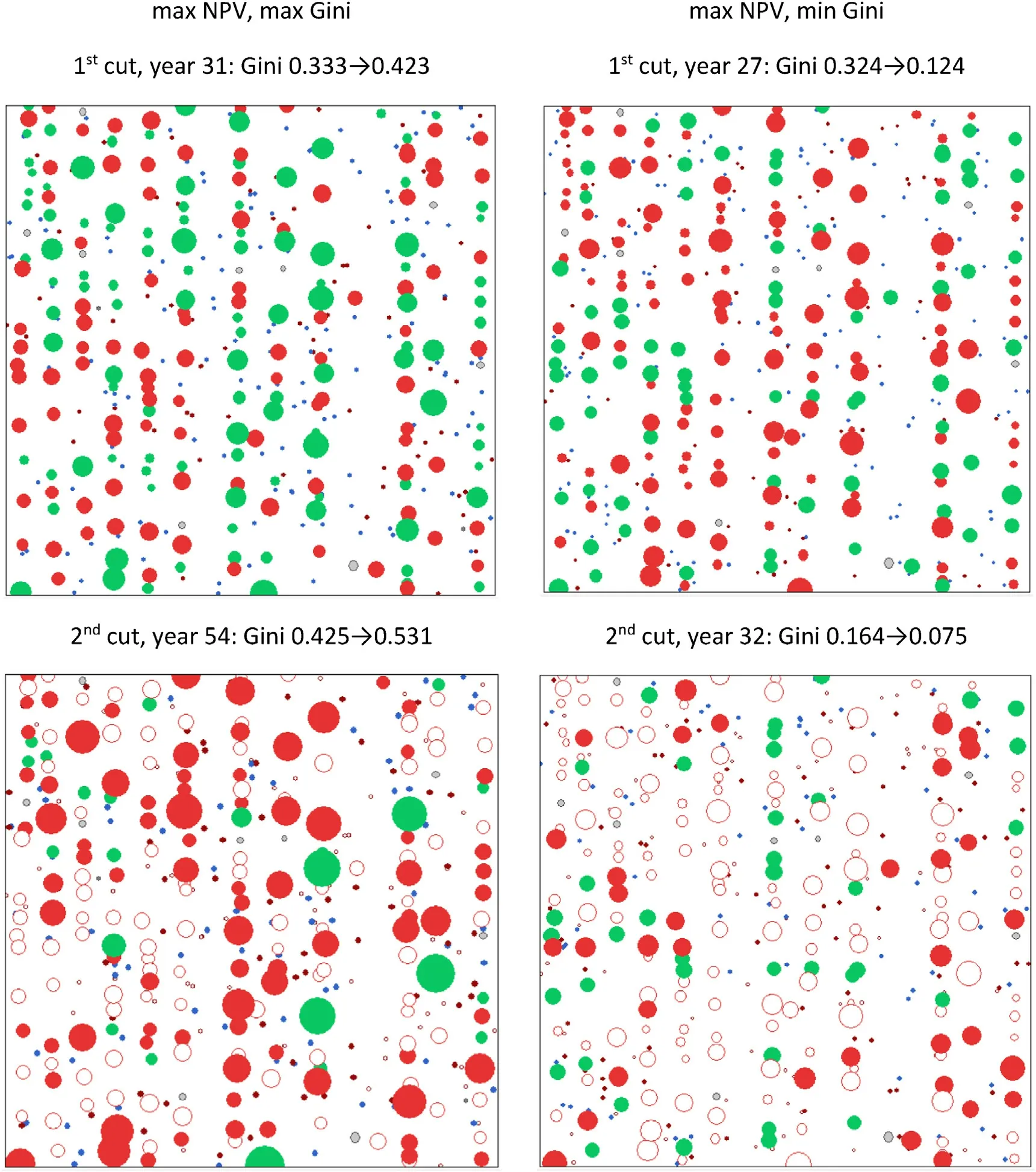
Fig.10.Tree map of the Larix olgensis sample plot at the first and second thinning when Gini index is maximized(left)or minimized(right)with the maximization of NPV.Remaining live trees are indicated with green(Larix olgensis)and blue(ingrowth of secondary species)color,trees that are removed in a particular cutting with red color(secondary species with darker tone),trees removed in earlier cuttings with open circles,and dead trees with grey color(secondary species with darker tone).The values of the Gini index before and after thinning are shown on top of the maps.(For interpretation of the references to color in this figure legend,the reader is referred to the Web version of this article.)

A common practical challenge in multi-functional forest planning is the difficulty to set the weights of the management objectives,which is necessary if the method described in this study is used for multi-objective optimization.There are methods to estimate the criteria weights(see for example Kangas et al.,2015) but the existence of a method does not guarantee that the weights reflect the true preferences of the decision-maker.A possible outcome is to solve the optimization problem with several different weights and use the results to draw trade-off curves between the objective variables (Selkim¨aki et al.,2020).By using the trade-off curves,the decision-maker can subjectively select the most satisfying combination of management objectives.

Forest plans are often developed for a certain planning period (for instance 10 or 20 years),and not for the entire rotation like in this study.Rotations do not even exist if the silvicultural system is continuous-cover forestry.When the management of an existing stand or forest is optimized for a certain fixed period,the NPV is calculated for the starting year of the planning period instead of the beginning of the rotation.The simulations cover only the period for which the management plan is developed.If the methods discussed in the current article are used in this type of forest planning,a model for the NPV of the ending growing stock is required if NPV is used as a management objective.This model predicts the net present value of all future management actions,implemented later than the last year of the planning horizon.

Fig.11.Development of basal area (top) and mean diameter (bottom) when NPV is maximized using a fixed starting temperature in simulated annealing(max NPV) or optimizing the starting temperature of simulated annealing simultaneously with the cutting years (max NPV,optimize SA).

Spatial or distance-dependent growth and survival models could be used in simulation instead of distance-independent models when the tree locations are known.For typical spatial distributions of tree locations,the predictions of distance-dependent models are not necessarily more accurate than those obtained from distance-independent models (Dong et al.,2021).However,if exceptionally irregular spatial patterns are targeted in forest management,or row or gap cuttings are used,the use of distance-dependent models is justified.Nevertheless,the simulation becomes more complicated with distance-dependent models,since the surroundings of the stands or plots need to be known to calculate the competition variables for trees near the stand edges.The simplest approach to overcome this problem is to assume that the surrounding forest is similar to the subject stand and to generate a temporary buffer zone of similar forest around the stand always when distance-dependent competition indices are calculated(Dong et al.,2021).

Stand-level growth models might be more reliable than individualtree models for predicting the yield of regular tree plantations.If this is the case,or there is a need to check the predictions against stand-level models,various calibration approaches such as the one described in Yue et al.(2008)can be used.

5.Conclusions

The study demonstrated that currently available optimization methods can be adapted to situations where treatment prescriptions are optimized for the individual trees of a stand.These methods can be used in economic optimization or multi-objective management.The approach demonstrated in this study is the most applicable to plantation forests.

Ethics approval and consent to participate

Not applicable.

Consent for publication

Not applicable.

Availability of data and material

The dataset used in the current study are available from the corresponding author on reasonable request.

Funding

This research was financially supported by the Natural Science Foundation of China (No.U21A20244 &No.32071758),and the Fundamental Research Funds for the Central Universities of China (No.2572020BA01).

Authors' contributions

YS and TP analysed the data and wrote the draft of the manuscript.XJ and FL acquired funding,supervised the work,and edited the manuscript.All authors read and approved the final manuscript.

Declaration of competing interest

The authors declare that they have no competing interests.

List of abbreviations

NPV Net present value