Radiative properties of alumina/aluminum particles and influence on radiative heat transfer in solid rocket motor

Xuefan HAO ,Hu ZHANG,* ,Xiao HOU ,Guihua TANG

a State Key Laboratory for Strength and Vibration of Mechanical Structures,Xi’an Jiaotong University,Xi’an 710049,China

b Shaanxi Key Laboratory of Environment and Control for Flight Vehicle,Xi’an Jiaotong University,Xi’an 710049,China

c College of Astronautics,Northwestern Polytechnical University,Xi’an 710072,China d Key Laboratory of Thermo-Fluid Science and Engineering,Ministry of Education,Xi’an Jiaotong University,Xi’an 710049,China

KEYWORDS Alumina;Aluminum;Condensed phase particle;Radiative heat transfer;Radiative properties;Solid rocket motor

Abstract The thermal radiation of micron-sized condensed phase particles plays a dominant role during the heat transfer process in aluminized Solid Rocket Motors(SRMs).Open research mainly focuses on the radiative properties of alumina particles while the study considering the presence of aluminum is lacking.In addition,the thermal radiation inside the SRM with consideration of the participating particles is seldom studied.In this work,the multiscale method of predicting the thermal environment inside SRMs is established from the particle radiation at microscale to the twophase flow and heat transfer at macroscale.The effective gray radiative properties of individual particles(alumina,aluminum,and hybrid alumina/aluminum)and particles cloud are investigated with the Mie theory and approximate method.Then a numerical method for predicting the thermal environment inside SRMs with considering particle radiation is established and applied in a subscale motor.The convective and radiative heat flux distributions along inner wall of motor are obtained,and it is found that the heat transfer in the combustion chamber is dominated by thermal radiation and the radiative heat flux is essentially a constant of 5.6-6.8 MW/m2.The convective heat transfer plays a dominant role in the nozzle and the heat flux reaches the maximum value of 11.2 MW/m2 near the throat.As the combustion efficiency of aluminum drops,the radiative heat flux remains unchanged in most regions and increases slightly along the diverging section wall of the nozzle.

1.Introduction

The specific impulse of Solid Rocket Motor (SRM) is usually improved by adding aluminum particles in the propellant due to their excellent calorific value and density.When the SRM is running,the combustion chamber undergoes severe thermal environment.For example,the interior temperature and pressure of the combustion chamber can be as high as 3800 K and 10 MPa,respectively.The micron-sized condensed phase particles generated from the combustion of aluminum have a significant impact on the internal flow and heat transfer process of the motor,including two-phase flow loss,slag formation,particles erosion and radiative heating.For aluminized SRM,the condensed phase particles play an important role in the total heat flux of thermal protection system of SRM and propellant combustion surface,as well as have a great influence on the radiative characteristics of plume.

To predict the thermal environment within SRM accurately,some efforts have been made to reveal the radiative properties of particles and the radiative heat transfer process inside the SRM by considering the thermal radiation of particles.Pearceproposed an approximate method to estimate the radiative heat flux between the two-phase combustion products and the wall of solid rocket nozzles.Der and Nelsoncalculated the emissivity of a cylindrical cloud of alumina particles using Monte Carlo method.Dombrovskiiinvestigated the radiative heat flux of the supersonic nozzle wall using one-dimensional flow model and two-dimensional radiation model.Duval et al.developed a numerical computational method for the prediction of radiative flux inside SRM with coupled solution between radiative heat transfer and multiphase turbulent flow,and applied it to the solid rocket boosters of the Ariane5.Jung and Brewsterdefined the effective gray radiative properties of alumina particles and performed a radiative heat transfer simulation on a subscale SRM with commercial computational fluid dynamics software Fluent.Furthermore,Crossinvestigated the radiative heat flux of two SRM nozzles with empirical model and numerical method.However,most of the existing studies were focused on the radiative characteristics and heat flux of plume,while the radiative heat transfer process inside SRM is scarcely reported,especially in the combustion chamber.

Another gap is that even though many studies that considering alumina particles have been conducted,the influence of the presence of alumina/aluminum particles(burning particles)in the motor was neglected.It is not only because of the complexity of combustion mechanism of aluminum particles,but also the expensive computational cost of simultaneously incorporating the combustion mechanism and radiative properties of alumina/aluminum particles.Some researchers have investigated the two-phase flow coupled with the combustion mechanism of alumina/aluminum particles,but the radiative heat transfer process considering participating particles in the SRM is not considered.For the radiative properties of alumina/aluminum particles,some approximate methods have been proposed.Harrison and Brewsterapplied the line-of-sight analysis to calculate the spectral radiative intensity distribution around the particle and compared it with the infrared radiation image of burning alumina/aluminum particle,and calculated the emissivity of alumina/aluminum particle.Besides,a method based on the assumptions of uniform and diffuse radiosity was also proposed for calculating the emissivity of alumina/aluminum particles.Based on Brewster and Harrison’s research on the emissivity of alumina/aluminum particles,Bityurin and Galaktionovsolved the radiative properties of alumina/aluminum particles with surface area weighted average method,and provided a convenient method for analyzing the effect of alumina/aluminum particles on the radiative heat transfer within aluminized SRM.

In summary,there is still lacking of research that focusing on the presence of condensed aluminum particles and investigating the flow and thermal environment inside the combustion chamber and the nozzle zone of SRM with considering the particle radiation.To overcome these deficiencies,the present work will study the radiative properties of alumina/aluminum particles and their influence on the radiative heat transfer process with considering the participating particles in an aluminized SRM.A multiscale method connected the radiative properties of condensed phase particles at microscale and the two-phase flow and heat transfer within SRMs at macroscale is established to predict the thermal environment inside solid rocket motors.Based on the Mie theory and the approximate method from Bityurin and Galaktionov,the radiative properties of individual alumina/aluminum particle is studied firstly.The influences of temperature,diameter and oxide cap thickness for an individual particle are investigated.For comparison,the radiative properties of alumina and aluminum particles will also be presented.Then,considering two diameter distributions of particles in the motor,the corresponding radiative properties of particles cloud and the impacts of temperature,diameter distribution and oxide cap thickness will be discussed.Finally,by considering the coupled thermal radiation and heat convection within SRM,the Eulerian-Lagrangian method for two-phase flow and discrete ordinates method for thermal radiation are adopted in the commercial software Fluent 17.0 to predict the thermal environment inside an SRM,and the influence of alumina/aluminum particles will be studied for the first time.

2.Methodology

The outline of methodology in this paper is illustrated in Fig.1.The Eulerian-Lagrangian method is adopted for the solution of two-phase flow field.The radiative properties of local particles cloud are calculated from the temperature and diameter distribution of particle phase obtained from twophase flow calculation and the radiative properties of individual particles obtained from Mie theory.The radiative properties of local particles cloud are input into the radiative transfer equation to obtain the distribution of radiation intensityand the heat source term by radiation in the energy equation.The solution of flow field and radiative heat transfer is coupled to get the flow and thermal environment considering radiation inside SRM,especially the radiative and convective heat fluxes at the wall.

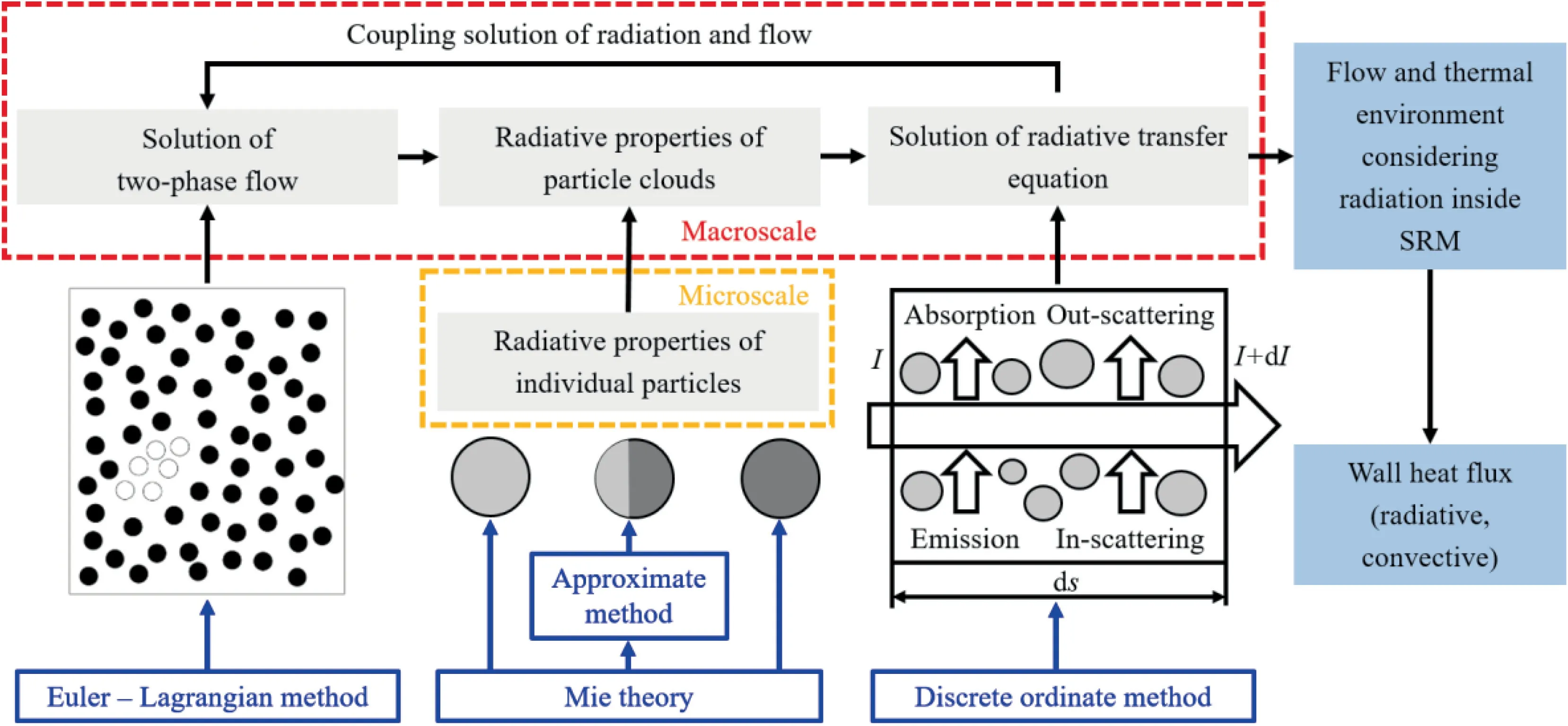
Fig.1 Methodology outline.

For the reliability verification of the methodology,at microscale the code of implementing Mie theory is validated with existing results from MIEV0while at macroscale the full-field radiative properties distribution (scattering and absorption coefficient)in the 75-lb(1 lb=0.4536 kg)BATES motor is calculated and compared with the results obtained by Jung and Brewster.Due to the complexity of the thermal environment in a real SRMs,the radiative properties and heat flux measurement inside SRMs are still lacking.

2.1.Radiative properties of individual particles

For an individual particle,the basic radiative properties include spectral scattering efficiency,spectral absorption efficiencyand spectral scattering phase function Φ.Many researcheshave proved that the alumina particles are nearly gray emitters for solid rocket motor with aluminized propellants.By using the gray body approximation,the calculation time for solving the radiative transfer equation with high resolution in spectral discretization can be reduced significantly.Therefore,the gray body approximation is adopted in this study and the effective gray radiative properties are analyzed in the simulation.The effective gray radiative properties can be obtained from the integration with respect to wavelength.

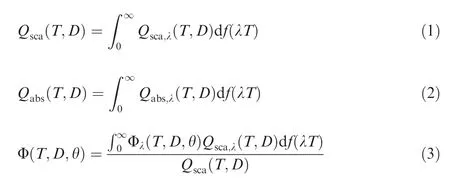
whereis the effective gray scattering efficiency,is the effective gray absorption efficiency,Φ is the effective gray scattering phase function,is the temperature of particle,is the diameter of particle,λ is the wavelength,θ is the scattering angle andis blackbody radiation function.

The radiative properties of alumina particles,aluminum particles and alumina/aluminum particles will be studied in present work.For an individual alumina particle and aluminum particle,their spectral radiative properties can be calculated by Mie theory.According to the Mie theory,the spectral scattering efficiency and spectral scattering phase function are calculated from the amplitude functionsand:

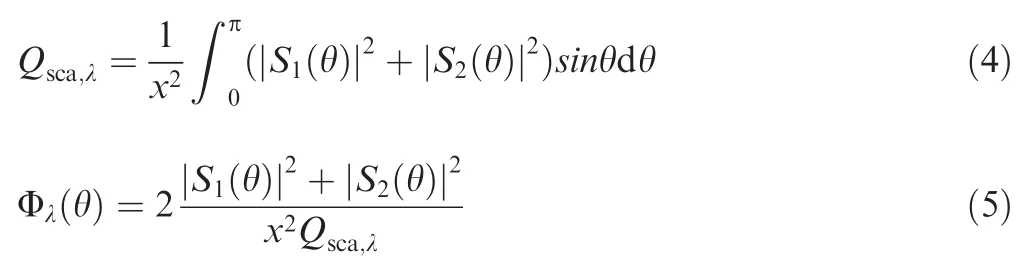
whereπλ is the size parameter.

The spectral extinction efficiency can also be calculated by the amplitude functionsand:

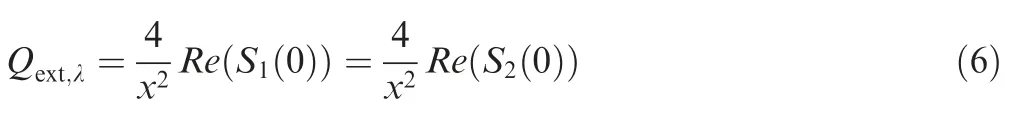
With the spectral extinction efficiency and the spectral scattering efficiency,the spectral absorption efficiency can be obtained by

In practical calculations,the amplitude functionsand,the spectral scattering efficiency and the spectral extinction efficiency are usually calculated from the following series:

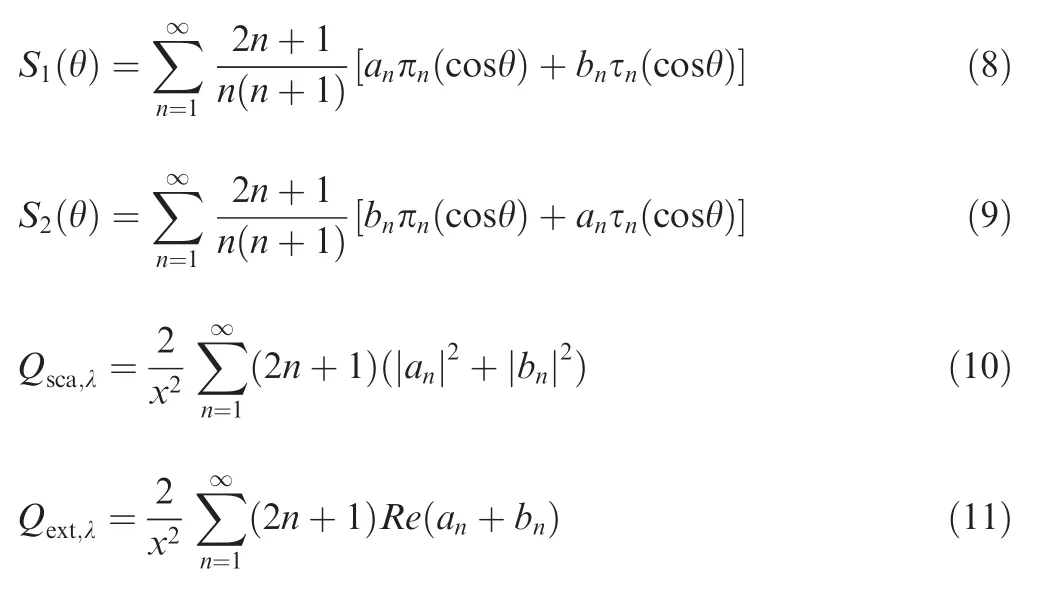
where aand bare Mie scattering coefficients,π(cos θ) and τ(cos θ)are scattering angle functions with cos θ as a variable and Re(a+ b) is real part of (a+ b).

Therefore,the spectral scattering efficiency,spectral extinction efficiency,spectral absorption efficiency,and spectral scattering phase function can be obtained by calculating the Mie scattering coefficients a,band scattering angle functions π(cos θ) and τ(cos θ).

The scattering angle functions π(cos θ)and τ(cos θ)can be calculated as follows.

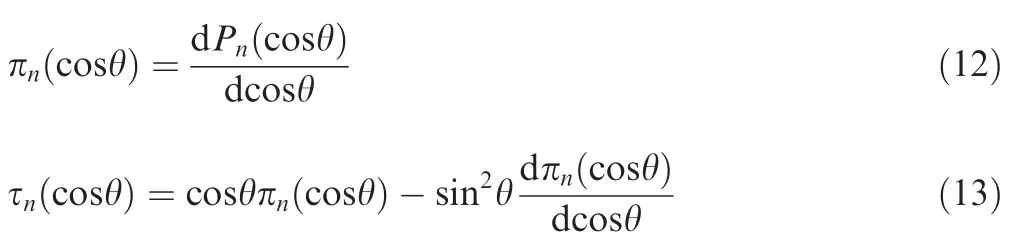
where P(cos θ)is the-order Legendre function with cos θ as a variable.

P(cos θ) is usually calculated from the following iterative formulas.

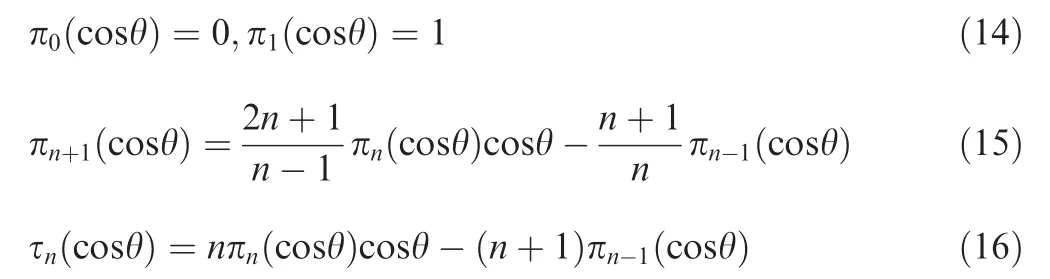
The calculation of Mie scattering coefficients aand badopts a continuous fractional algorithm with expressions of

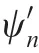
ψand ζcan be expressed as

where J() is+1/2 order Bessel function of the first kind,H()is+1/2 order Hankel function of the second kind,and Y()is+1/2 order Bessel function of the second kind.

In the calculation,the first kind and second kind of Bessel functions of the+1/2 order can be calculated by calling the‘‘besselj”and‘‘bessey”functions built in MATLAB,and the calculation of the first derivative of them can use the following iterative formulas.

The continuous fractional function D() is calculated from iterative formulas:

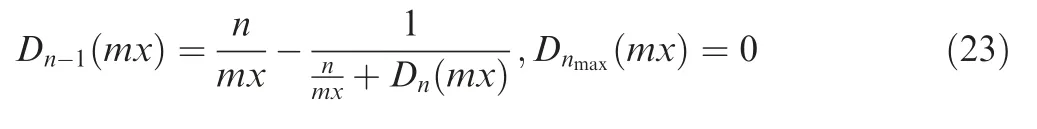
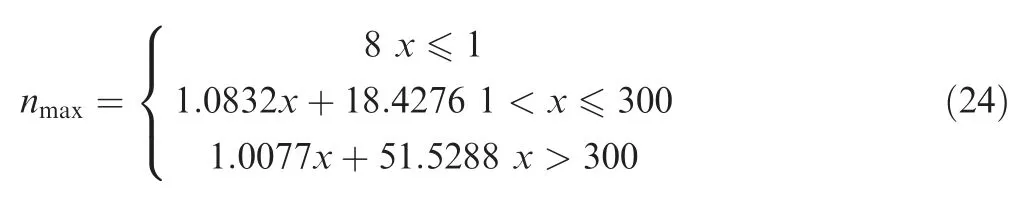
As shown in Fig.2,the calculation process of applying Mie theory is summarized.To obtain effective gray scattering efficiency,the effective gray absorption efficiencyand the effective gray scattering phase function Φ,the input parameters,including the particle diameter,temperatureand complex index of refractionshould be known beforehand.

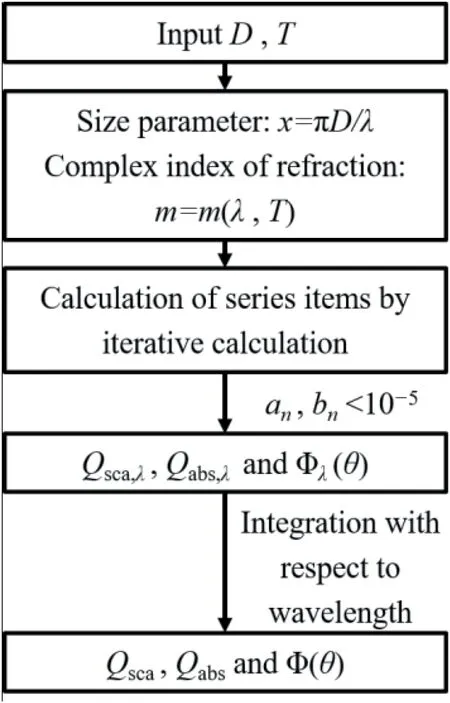
Fig.2 Calculation flow chart of applying Mie theory.

Therefore,for alumina and aluminum particles,the three main input parameters are the functions of particle diameter,temperatureand complex index of refraction-i(is the refractive index,is the absorption index and i is the imaginary unit).Besides,the complex index of refraction is also the function of wavelength λ and particle temperature.In this study,the refractive and absorption indexes of alumina are calculated using Dombrovsky correlation and Bakhir correlation,respectively.The complex refractive indexes of aluminum are calculated using the Drude model.

For the individual alumina/aluminum particle shown in Fig.3,an approximation method proposed by Bityurin and Galaktionov is adopted.The method assumes that the spectral radiative properties of individual alumina/aluminum particle can be obtained from the spectral radiative properties of the alumina and aluminum particles with the same size and temperature by weighted averaging the surface areas occupied by alumina and aluminum.For an alumina/aluminum particle with diameterand alumina cap thickness,the spectral radiative properties can be calculated by the following formulas.

Fig.3 Schematic diagram of calculation method for alumina/aluminum particle.

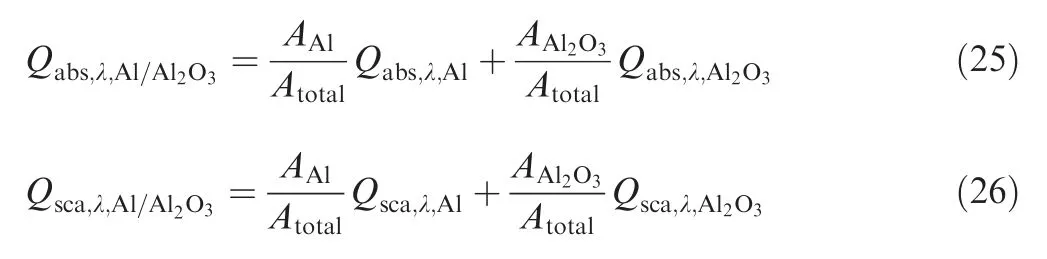
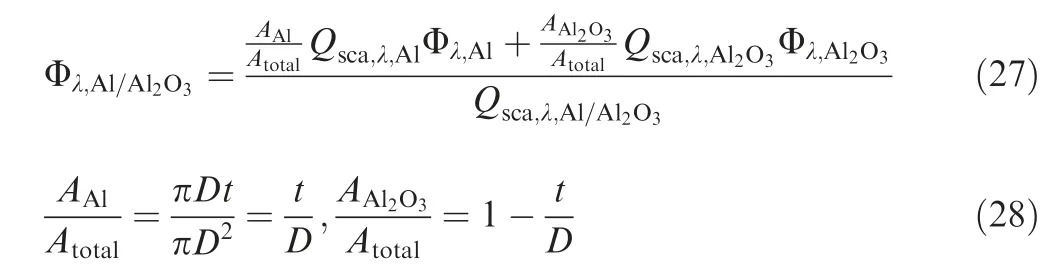
whereis the surface area of alumina/aluminum particle,andare the surface area occupied by alumina and aluminum in the alumina/aluminum particle,respectively,and the detailed derived process can be found in Ref.27.

The calculation of the radiative properties of alumina/aluminum particle is simplified to calculate the radiative properties of aluminum and alumina particles using the Mie theory.The reliability of the radiative calculation model of aluminum/alumina particle has been verified experimentallyand the Eqs.(25)-(27)are proposed based on these experiment results.Rigorous electrodynamics calculation could verify the model strictly,but the computational cost is huge and beyond the objective scope of this paper.So the reliability of developed MATLAB calculation code for implementing Mie theory is validated by comparing the results from MIEV0(see Appendix Table A1) and the maximum relative deviation (%) is below 5.8 × 10,indicating that the Mie theoretical calculation is reliable.

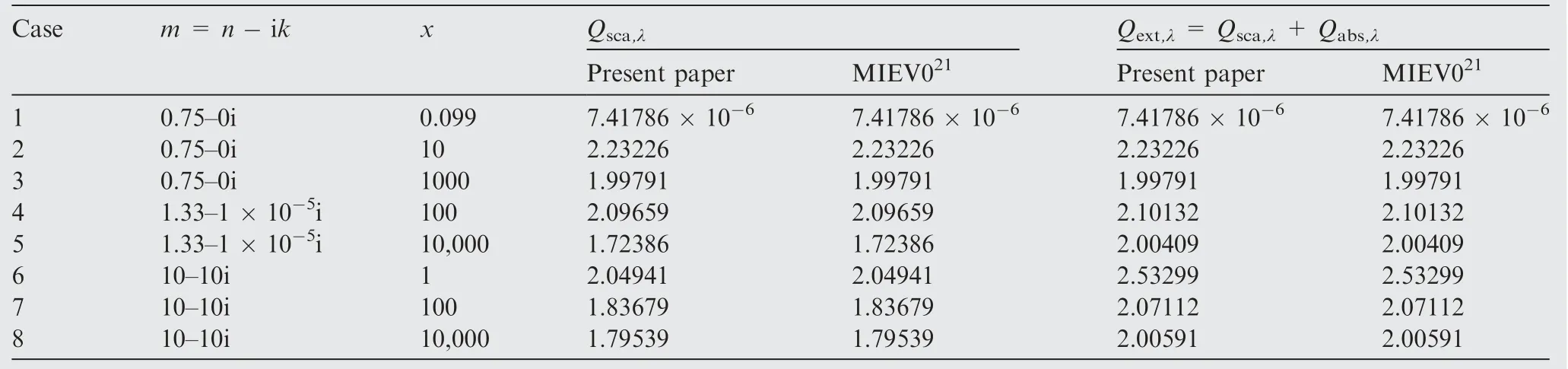
Table A1 Comparison of Mie theory algorithm.

2.2.Radiative properties of particle cloud

To calculate the radiative heat transfer within the combustion chamber and nozzle of solid rocket motor quantitatively,the radiative properties of particles cloud with specific particle number density and particle size distribution should be known and incorporated into the radiative transfer equation.In the radiative transfer equation for thermal radiation participating medium,the radiative parameters including effective gray absorption coefficient,effective gray scattering coefficientand effective gray scattering phase function of particles cloud Φcan be obtained from

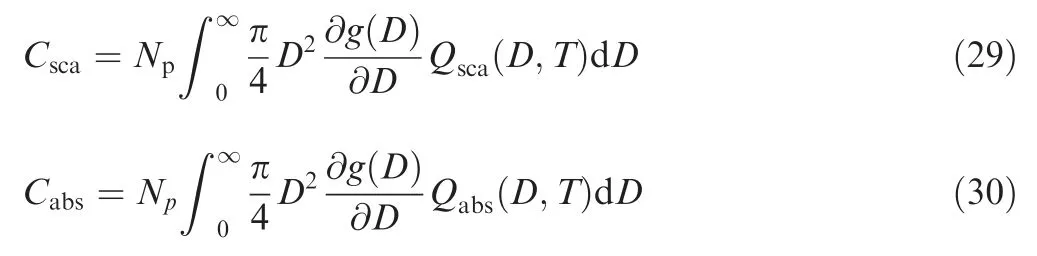
whereis the particle number density and()is the particle number fraction cumulative distribution function.

To obtain the effective gray radiative properties of particle cloud,the influences of individual particles,particle size distribution and particle number density are taken into account.In this section,two typical particle size distributions proposed by Crossis adopted.The corresponding particle size distributions and particle number densities are shown in Fig.4.Distribution A represents the particle size distribution at the nozzle outlet,and Distribution B represents the particle size distribution at the nozzle inlet.If ignoring the collision,fragmentation and coalescence of particles in the combustion chamber,Distribution B can also represent the particle size distribution in the combustion chamber.

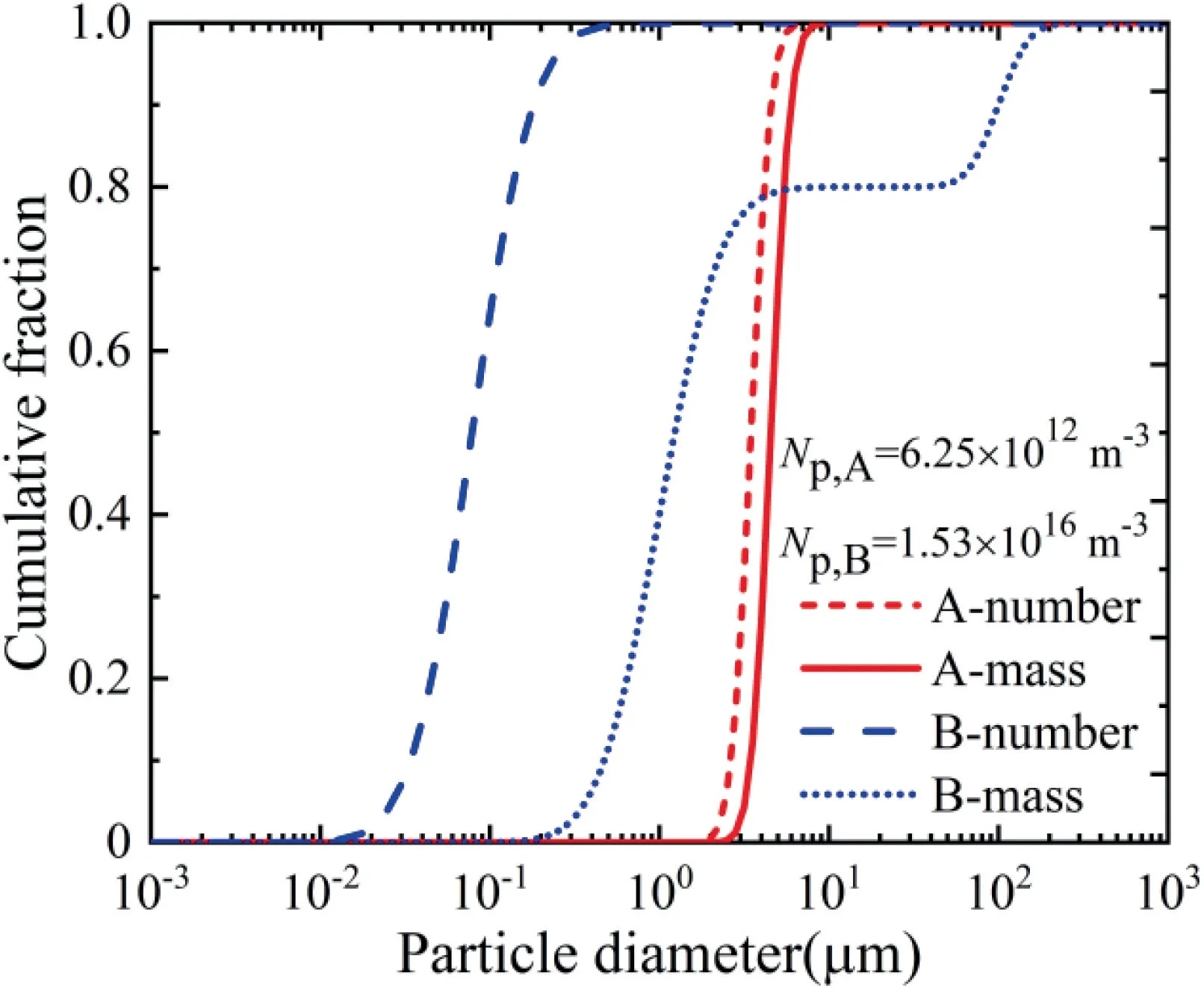
Fig.4 Mass and number cumulative fractions for two particle size distributions.11

The number density of particles is calculated from Eqs.(32)and (34).A typical temperature of 3000 K in the motor is taken to determine the density of condensed phase particles.The mixture density and particle mass fraction are taken from Ref.11,1.5 kg/m,0.3023 for Distribution A and 1.5 kg/m,0.2419 for Distribution B.Note that the particle number density of Distribution A is three orders of magnitude lower than that of Distribution B.The particles accelerate rapidly in the nozzle,and thus the particles become sparse in the downstream of the nozzle.

where ρis the density of particle-gas mixture,ρis the density of particle,is the mass fraction of particle,is the number averaged mean particle volume.

2.3.Two-phase flow and radiation modeling

The two-phase fluid field within SRM is calculated using the Eulerian-Lagrangian method,in which the governing equations for the gas phase are

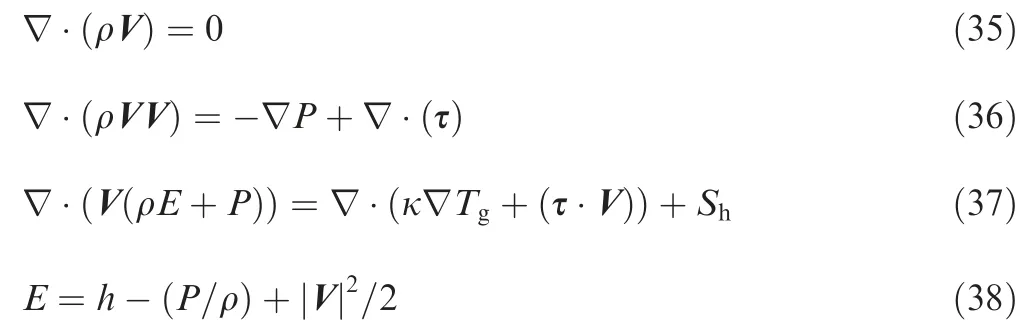
where ρ is the gas phase density,V is the gas phase velocity,is the pressure,τ is the shear stress,is the total energy,κ is the gas phase thermal conductivity,is the gas phase temperature,is the radiant heat source term andis the gas phase enthalpy.

The motion governing equations of the condensed phase particles in the fluid field are

where Vis the particle velocity, F(V-V) is the resistance per unit mass of particles,μ is the gas-phase dynamic viscosity,Cis the resistance coefficient andis the Reynolds number.

For the heat transfer of particles,the convection between particles and gas,and the radiative heat transfer among particles and the surfaces are considered

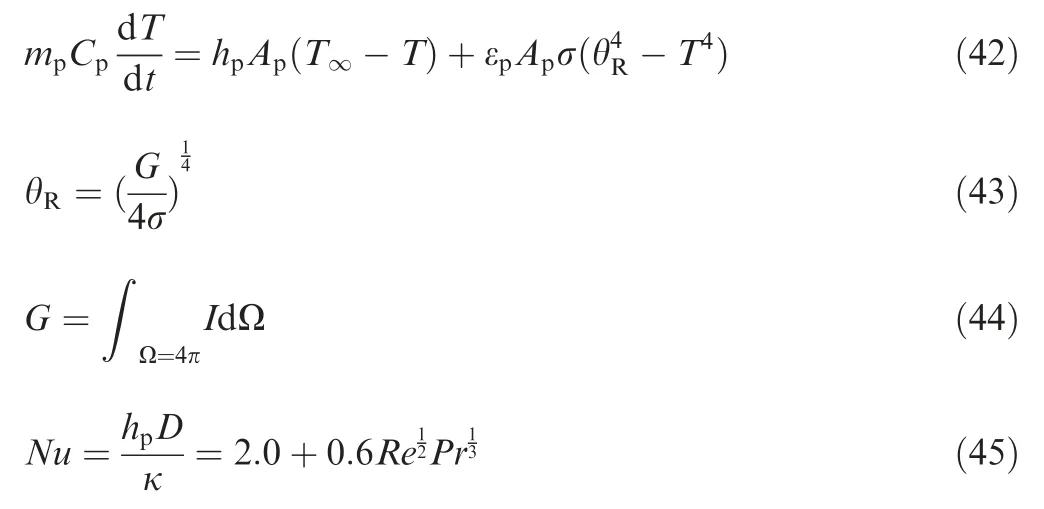
whereis the particle mass,is the particle specific heat,is the particle surface area,is the local gas phase temperature,is the particle convection heat transfer coefficient,εis the particle emissivity,σ is the Stefan Boltzmann constant,θis the radiant temperature,is the incident radiation,Ω is the solid angle,is the Nusselt number,andis the gas phase Prandtl number.

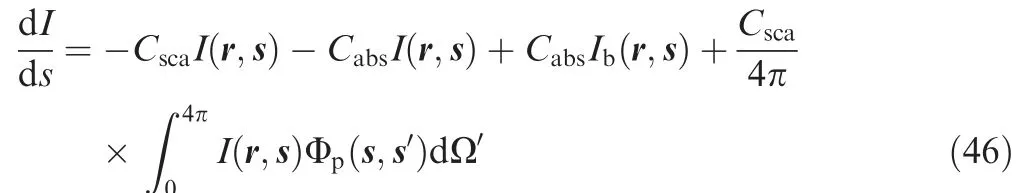
The Radiative Transfer Equation (RTE) of particle participating medium iswhere r is the position vector,s is the unit direction vector,sis the unit scattering direction vector,is the distance light travels in a unit direction vector s,Ωis the spatial angle andis the local blackbody radiation intensity.The method of solving RTE will be introduced in Section 2.5.

Some researchershave pointed out that the contribution of gas to the radiative heat flux can be neglected compared to the contribution of condensed phase particles in the aluminized solid rocket motor.In addition,the objective of this work is to study the radiative properties of alumina/aluminum particles and their influence on the radiative heat transfer in solid rocket motor,thus the contribution of gas is not considered in the simulation.

2.4.Simulated motor and computational grid

The calculated case is a 75-lb ballistic test and evaluation system motor (75-lb BATES).Its geometric parameters are shown in Fig.5.

Fig.5 Schematic diagram of 75-lb BATES.

The computational domain is meshed with quadrilateral structural grid and the refinement mesh is generated in localized areas.Five sets of grids are selected for meshindependence check.The grid numbers are 5000,10000,15000,25000,and 33000.The Mach numbers () along the symmetry axis obtained from five grids are compared in Fig.6.The result shows that the calculated Mach numbers with different grid numbers are almost the same in most areas except for the region around=0.8 m.The maximum relative difference of Mach number calculated from the 33000 grid and the 25000 grid is less than 1%,thus the 25000 grid as shown in Fig.7 is chosen in the following simulation.

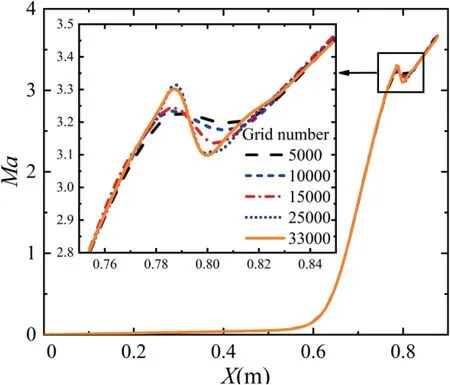
Fig.6 Mach number along symmetry axis.

2.5.Numerical method and boundary condition

The commercial software Fluent 17.0 is employed to simulate the two-phase flow and heat transfer in the motor by considering the particle thermal radiation.In terms of the model setting,the discrete phase model based on the Eulerian-Lagrangian method is adopted to solve the two-phase fluid field,and the discrete phase calculation is performed every 50 steps of the fluid field calculation.The RNG-ε turbulence model with the standard wall function treatment near the wall is selected.The discrete coordinate method with spatial angle discretization of 3 × 3 and wavelength range of 0.5-8 μm is chosen to solve the radiative transfer equation since it is suitable for both optical thick and optical thin medium.Radiative transfer equation is solved every 10 steps of the fluid field calculation.

The boundary condition is set as presented in Fig.7.According to the experimental dataand the numerical simulation settings,the gas phase mass flow rate is set as 6.77 kg/s.For the particle phase,five groups of particles are used to represent particles cloud with bimodal distribution.The particle sizes are set as 1.2,60,110,180,260,and 340 μm,and the corresponding mass flows are 2.48,0.25,0.05,0.15,0.1 and 0.2 kg/s,respectively.The temperature of gas phase and particle phase is set at 3655 K,the same as the temperature of combustion chamber.The motor head and the nozzle wall are set to be adiabatic,non-slip,and non-penetrating.When the particles reached the wall,they will be captured by the wall to simulate the deposition of particles on the wall.The central axis of the motor is the symmetry axis.When the particles arrived at the symmetry axis,they will be reflected.The outlet pressure of the nozzle is 101325 Pa and the temperature is 300 K.The temperature of the burning surface is set as 1000 K.For the calculation of thermal radiation,the emissivity of burning surface is set as 0.95,the motor head and the nozzle wall are opaque and diffuse gray surfaces,and their emissivity are 0.9.The plume at the outlet is considered to be opaque and nonreflective,and the emissivity at the nozzle outlet is 1.

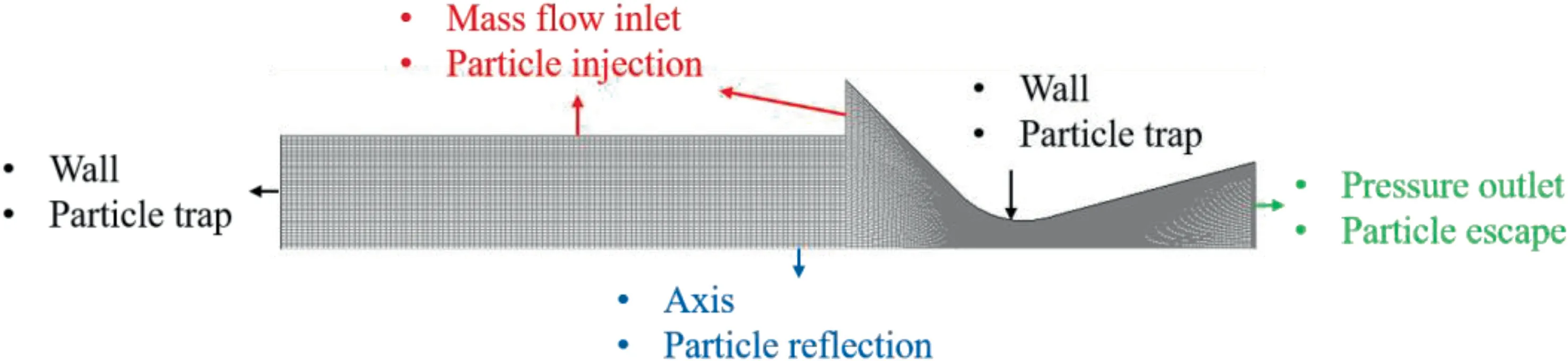
Fig.7 Schematic diagram of the grid and boundary conditions.

In terms of the material properties,the density of gas is calculated using the ideal gas model,while the other thermophysical properties are simulated using those of air.The density of alumina is 2800 kg/mand the specific heat capacity is 1525 J/(kg·K).When the influence of alumina/aluminum particles is taken into account,the density of aluminum is 1800 kg/mand the specific heat capacity is 1177 J/(kg·K).The thermophysical properties of alumina particles and alumina/aluminum particles are input into the Fluent software using User-Defined Function(UDF).The complex refractive indexes of alumina and aluminum are taken from the experimental dataand the Drude model,respectively.

The effective gray scattering coefficient and absorption coefficient of local particles cloud can be calculated using the effective gray scattering and absorption efficiency curves by the UDF and the temperature and particle size distributions are obtained from two-phase flow calculation.Up to now,the anisotropic scattering effect of particles is still not supported by mainstream commercial CFD software such as FLUENT,STAR-CCM+and CFX.Some researchershave studied the effect of anisotropic scattering of particles and found that small sizes particles(～1 μm),which accounting for the majority of the total mass flow and dominating the radiation heat transfer process of the solid rocket motor,behave more isotropically.Therefore,the isotropic scattering assumption is adopted in this work.

In terms of the solution setup,the pressure-based solver and the SIMPLE algorithm are adopted.The space is discretized with second-order upwind scheme.The hybrid initialization method is used to calculate the gas-phase fluid field and then the result is used as the initialized fluid field for the twophase flow calculation.The average pressure at the motor head is monitored during the calculation and the fluid field is converged when the residuals and pressure change are less than 10.

2.6.Validation case

To verify the present numerical simulation method,the distributions of scattering coefficient and absorption coefficient in the 75-lb BATES motor are calculated and compared with the results that obtained by Jung and Brewster.It is worth noticing that since the values at different nodes are not available in Jung and Brewster’s work,only the contours and the values at some typical regions in the solid rocket motor are compared.Generally,the comparison shows good agreement as shown in Figs.8 and 9,which implies that the numerical method used in this study is reliable.

Fig.8 Absorption coefficient distributions calculated by Jung and Brewster10 (left) and present simulation (right).

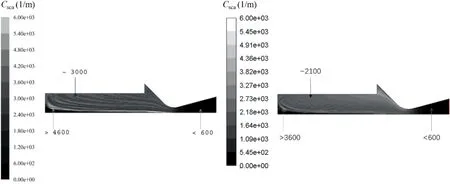
Fig.9 Scattering coefficient distributions calculated by Jung and Brewster10 (left) and present simulation (right).

To simulate a more realistic internal thermal environment of the SRM,the convective heat transfer at the motor head and the nozzle wall is considered while the wall was set as adiabatic by Jung and Brewsterto calculate the distribution of radiative properties.The head and nozzle wall are assumed to be isothermal with temperature of 1000 K.Owing to the limitation of commercial software,the convective heat transfer at the burning surface is not considered in this study.

After obtaining the internal fluid field and thermal environment of the motor with considering the convective heat transfer and particle thermal radiation,the influence of unburned aluminum ratio(the combustion efficiency of aluminum drops)on the radiative heat flux in the motor is investigated.For simplification,all the alumina/aluminum particles in the motor are assumed to have the same cap thickness ratio/.

3.Results and discussion

3.1.Radiative properties of individual particles

In Figs.10 and 11,the effective gray radiative properties of individual alumina particle at different temperatures and diameters are presented.

As shown in Fig.10,the scattering efficiency of individual alumina particle increases with temperature at small diameter(=0.1 μm).However,with the increase of particle diameter,the scattering efficiency increases firstly,and then decreases with temperature at a large size(=1 μm)and finally transits to a monotonically decreasing trend with temperature for even larger size particle(=10,100 μm).The absorption efficiency of individual alumina particle shows an increasing trend with temperature for different diameters (=0.1,1,10,100 μm).

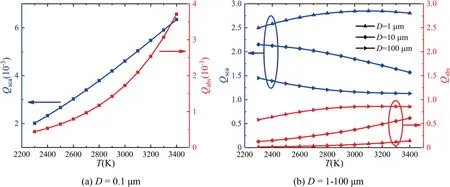
Fig.10 Effective gray scattering and absorption efficiencies of individual alumina particle.

As shown in Fig.11,the absorption efficiency of individual alumina particle increases with particle diameter at different temperatures except a slight decrease at=3400 K.The scattering efficiency of an individual alumina particle firstly increases and then decreases with diameter at different temperatures and reaches the peak value at～1 μm.For the scattering phase function,it hardly changes with temperature,but gradually shifts from anisotropic to isotropic with decreasing particle diameter.

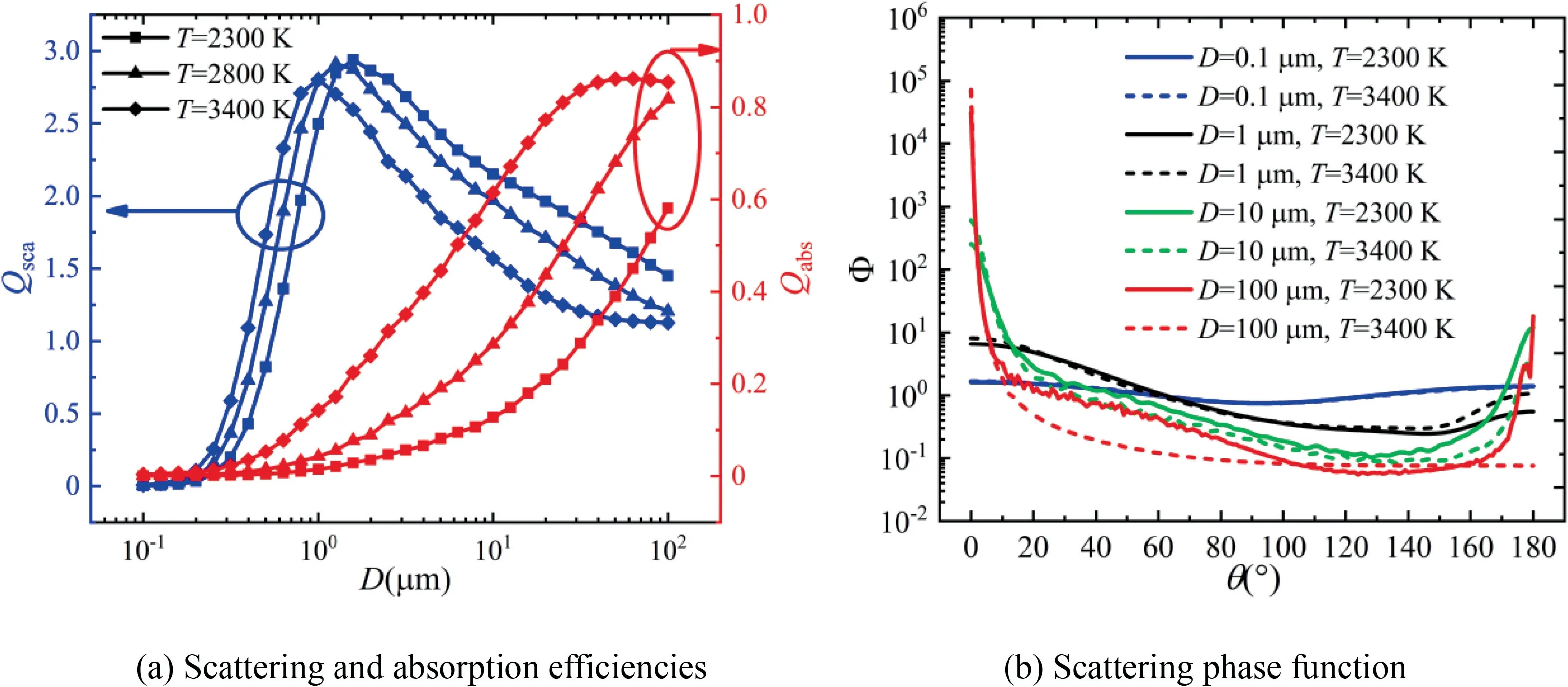
Fig.11 Effective gray radiative properties of individual alumina particle.

The variation of complex refractive index of alumina and aluminum is presented in Fig.12.The variations in Figs.10 and 11 can be explained by the variation of complex refractive index of alumina in Fig.12(a) and the scattering regimes in Fig.13.Although the radiative properties of particles are function of its complex refractive index according to the Mie theory,the scattering of particle is dominated by refractive index and weakly influenced by absorption index while absorption of particle is dominated by absorption index and weakly influenced by refractive index.As shown in Fig.12(a),the refractive index increases slightly with temperature while the absorption index increases drastically.In addition,the increments of refractive and absorption indexes directly affect the optical cross-section (πD,πD) instead of the optical efficiencies(,).Hence,the influence of temperature(or refractive index)is dominant at=0.1 μm.With the increase of πD,the scattering efficiency transits to decrease gradually in Fig.10(b),but the absorption efficiency is still increasing because of the increasing absorption index.In Fig.11(a),with the increment of diameter,πDincreases faster than πDwhen the diameter is no higher than 1 μm,thus the scattering efficiency maintains an increasing trend.Then the increase of πDis dominant and the scattering efficiency transits to decrease.The similar trend can be found in the variation of absorption efficiency in Fig.11(a) while the influence of πDis weaker than the increasing absorption index.

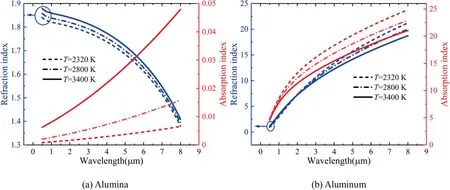
Fig.12 Complex refractive indexes of alumina and aluminum.

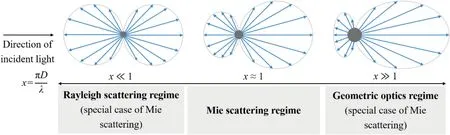
Fig.13 Three kinds of scattering regime for particles with different diameters.

The variation of scattering phase function in Fig.11(a)can be explained by the scattering mode of particles with different size diameter in Fig.13.When the size parameteris much less than 1 (e.g.=0.1 μm),the scattering is almost isotropic except the side direction and usually called Rayleigh scattering regime.When the magnitude ofis similar to 1 (e.g.=1 μm),the scattering is fully anisotropic due to the wave interference and usually called Mie scattering regime.Whenis much larger than 1 (e.g.=100 μm),the scattering is highly forward-anisotropic due to the stronger wave interference and usually called Geometric optics regime.Since the transition of scattering regime mainly depends on the size parameter,the scattering phase function varies with scattering mode and weakly influenced by temperature whenincreases from 0.1 μm to 100 μm.

In Figs.14 and 15,the effective gray radiative properties of individual aluminum particle at different temperatures and diameters are presented.

As shown in Fig.14,the scattering efficiency of aluminum particle shows a similar trend with the correspondent case of alumina particle.However,the absorption efficiencies of aluminum particles with different diameters all increase with temperature.As shown in Fig.15,both the scattering efficiency and absorption efficiency of aluminum particle increase firstly and then decrease with diameter at different temperatures,and the corresponding peaks are all around=1 μm for the scattering efficiency and=0.4 μm for the absorption efficiency.The scattering phase function of aluminum particle almost invariant with temperature,but gradually shifts from anisotropic(more specifically,dominated by forward scattering)to isotropic with the increment of particle diameter.

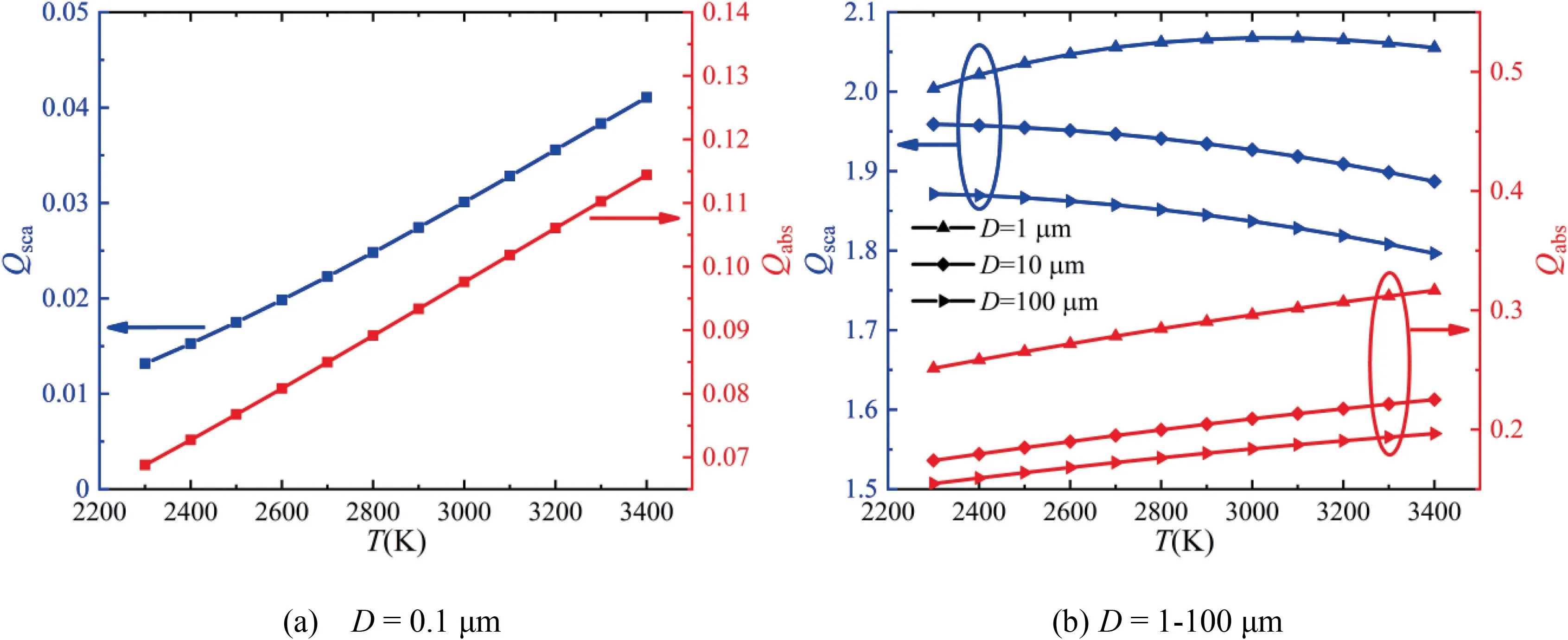
Fig.14 Effective gray scattering and absorption efficiencies of individual aluminum particle.

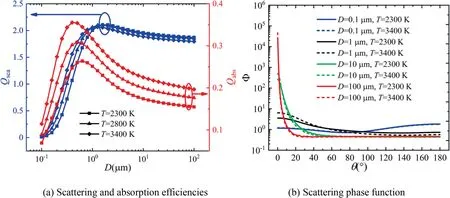
Fig.15 Effective gray radiative properties of individual aluminum particle.

In summary the scattering and absorption efficiencies of individual alumina and aluminum particles have a similar trend with temperature and diameter but possess a notable difference in quantity.As shown in Fig.12(b),both the refractive and absorption indexes of aluminum decrease slightly with temperature in most of the wavelength range.The variation of aluminum is opposite to that of alumina,but the variation of optical efficiency is very similar.This could be explained by the significant differences in the quantity of indexes (both the refractive and absorption indexes of aluminum are an order of magnitude higher than those of alumina).

As shown in Fig.16,the influence of temperature on the effective gray radiative properties of alumina/aluminum particle at different diameters and cap thickness ratios()are presented.The scattering phase function of alumina/aluminum particle is hardly affected by temperature and cap thickness ratio,and becomes more anisotropic with increasing particle diameter.This can be explained by the transition of scattering regime.The absorption efficiency increases with temperature for different diameters and cap thickness ratios while the scattering efficiency increases at small diameter firstly and then gradually transits to a decreasing trend at large diameter with temperature.From Eqs.(25)-(28),the optical efficiencies of alumina/aluminum particle are linear weighted superposition of the optical efficiencies of alumina particle and aluminum particle.Due to the similarity of alumina and aluminum particles in the variations of the scattering and absorption efficiencies with temperature,the alumina/aluminum particle also shows a similar trend.

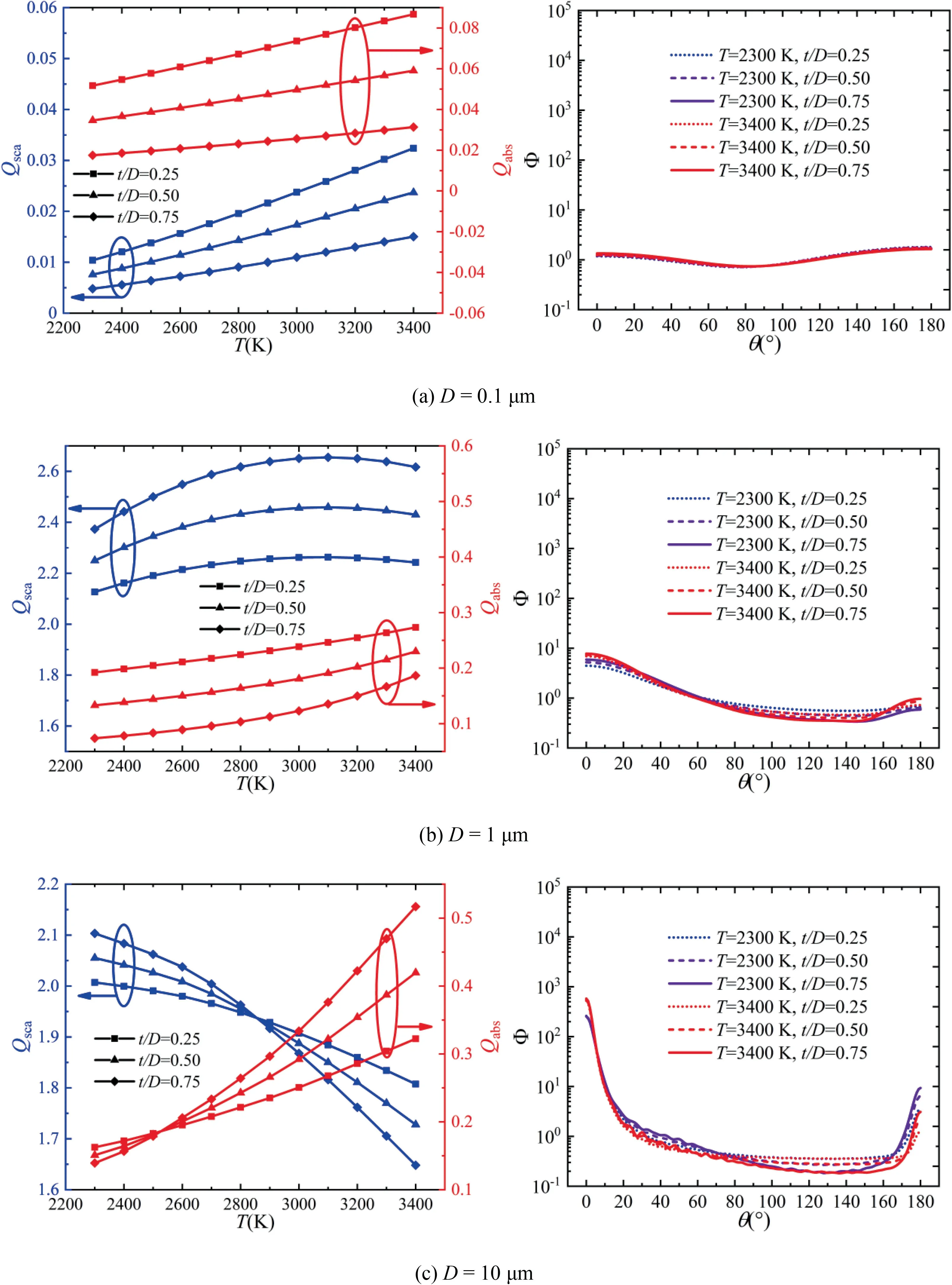
Fig.16 Influence of temperature on effective gray radiative properties of alumina/aluminum particle.

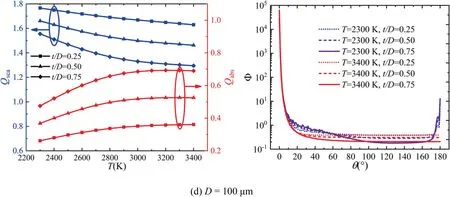
Fig.16 (continued)

As shown in Fig.17,the influences of diameter on the optical efficiencies of alumina/aluminum particle at different temperatures and cap thickness ratios () are presented.As the diameter increases from 0.1 to 100 μm,the scattering efficiency increases firstly and then decreases from about 1 μm at different temperatures and cap thickness ratios,which is similar to the individual aluminum and alumina particles.However,the absorption efficiency of alumina/aluminum particle shows a roughly increasing trend with diameter.This variation keeps consistent with the absorption efficiencies and scattering efficiencies of both individual aluminum and alumina particles.This phenomenon can also be explained by the linear weighted superposition.The similarity of alumina and aluminum particles in the variation of optical efficiencies with diameter leading to the similar behavior of alumina/aluminum particle.However,the influence of the cap thickness ratio () on the optical efficiencies of alumina/aluminum particle is not significant,as shown in Figs.16 and 17.This is caused by the close values of optical efficiencies for alumina and aluminum particles in Figs.10,11(a),14 and 15(a).

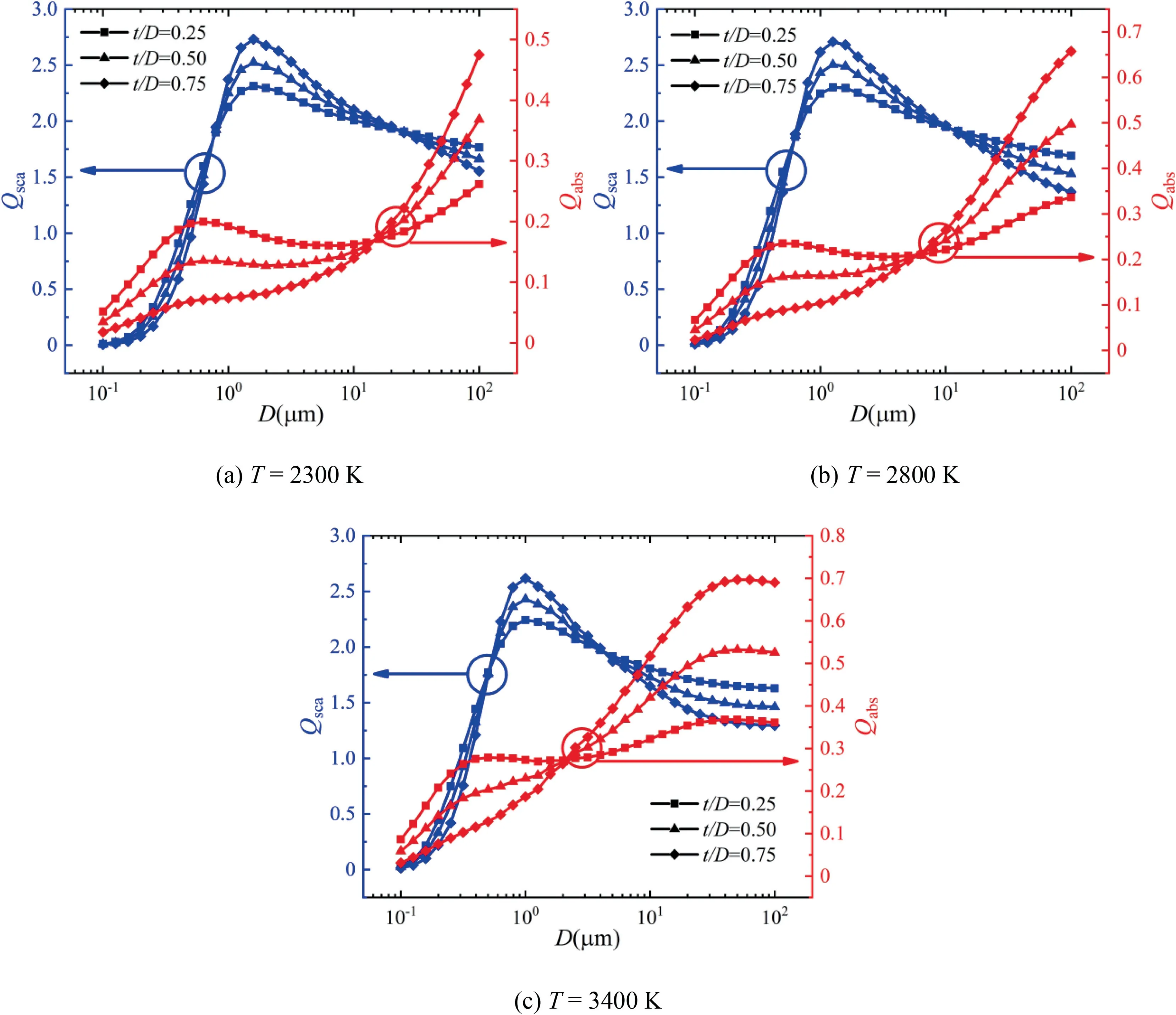
Fig.17 Influence of diameter on optical efficiencies of alumina/aluminum particle.

3.2.Radiative properties of particle cloud

The effective gray radiative properties of alumina particles cloud with different diameter distributions are presented at different temperatures in Fig.18.With the increase of temperature,the scattering coefficients of alumina particles cloud increase for Distribution B but decrease for Distribution A.The absorption coefficients increase with temperature for both Distributions A and B.This can be explained by the number distribution of particle diameter in Fig.4.The dominant particle size for Distributions A and B are～3 μm and～0.1 μm,respectively.As shown in Fig.10,the absorption efficiency of individual alumina particle shows an increasing trend with temperature for different diameters,thus the absorption coefficient increases for both distributions.The scattering efficiency of individual alumina particle increases with temperature for=0.1 μm and decreases with temperature for=10,100 μm,thus the scattering coefficient increases for Distribution B (～0.1 μm) but decreases for Distribution A (～3 μm).For the scattering phase function,it is essentially invariant with temperature and closer to isotropic scattering for Distribution B than Distribution A.Since the diameters of dominant particles in number Distribution B (～0.1 μm) is much less than that of A (～3 μm),the Distribution B is closer to isotropic scattering than Distribution A.

As shown in Fig.19,the effective gray radiative properties of aluminum particles cloud with different diameter distributions are presented at different temperatures.With the increase of temperature,the scattering coefficients of alumina particles cloud increase for Distribution B but decrease for Distribution A.Meanwhile,the absorption coefficients increase with temperature for both Distributions A and B.This phenomenon can also be explained by the number distribution of particle diameter in Fig.4 and the behavior of individual aluminum particle in Fig.14.The explanation is the same as that of alumina particle cloud.For the scattering phase function of aluminum particles cloud,although there are back-scattering peaks in Fig.18(b) and there is not in Fig.19(b),its influence is weak compared to forward scattering peaks.So,in generally,scattering phase function of aluminum particles behaves like alumina particles.

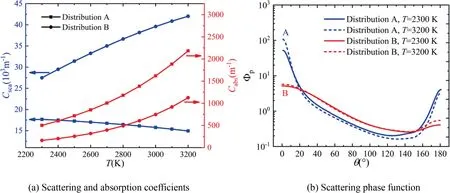
Fig.18 Effective gray radiative properties of alumina particle cloud.

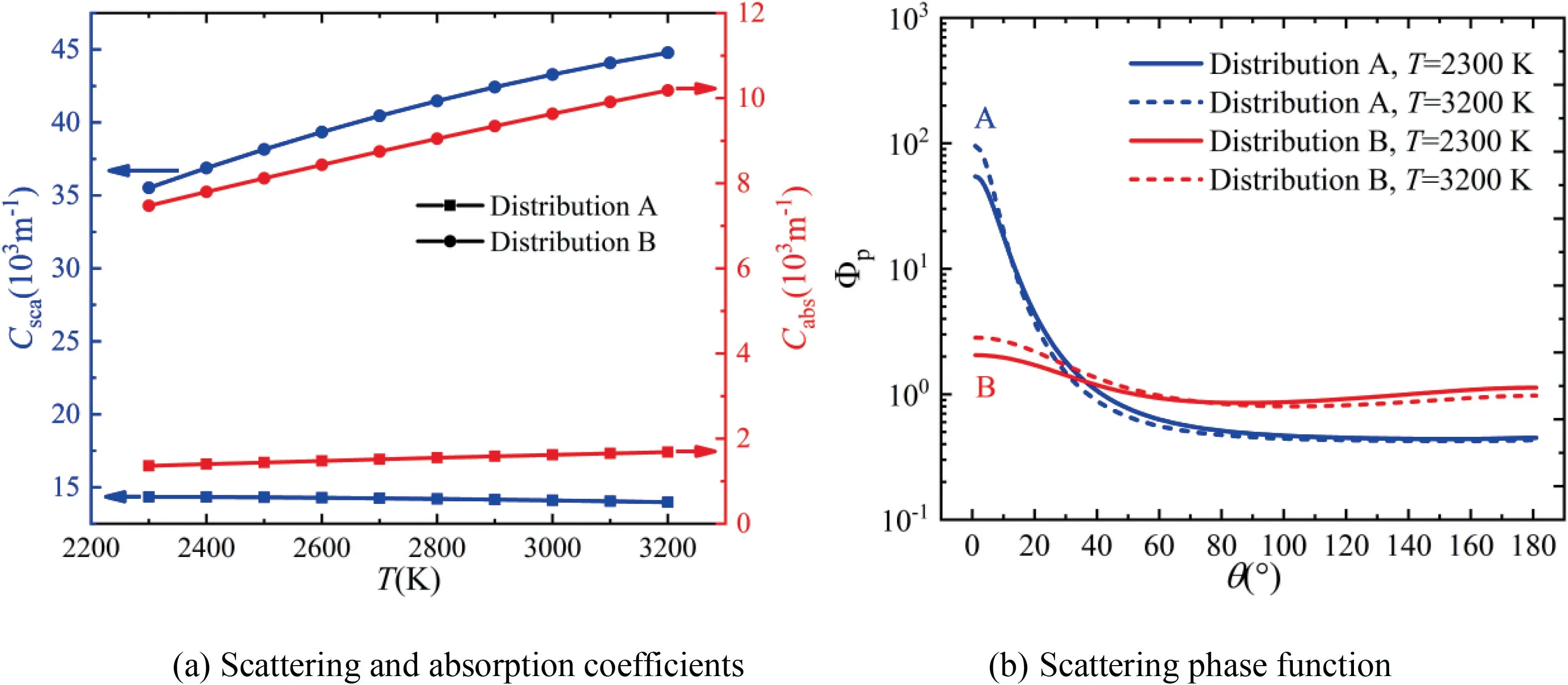
Fig.19 Effective gray radiative properties of aluminum particle cloud.

Overall,the variations of effective gray radiative properties of alumina particles cloud and aluminum particles cloud are very similar.The behavior of numerically dominant individual particles controls the behavior of correspondent particle cloud.

As shown in Fig.20,the effective gray radiative properties of alumina/aluminum particles cloud with different cap thickness ratios () are obtained at different temperatures for diameter Distribution A.Similar to the alumina and aluminum particles cloud with diameter Distribution A,the scattering coefficient of alumina/aluminum particles cloud decreases with temperature while the absorption coefficient increases with temperature.This is caused by the patterns changes in alumina particles cloud and aluminum particles cloud with temperature are inherently similar.With the increase of cap thickness ratio(),the scattering coefficient increases for Distribution A.The absorption coefficient decreases with the cap thickness ratio at temperature lower than 3000 K and then increases at higher temperature for Distribution A.It is due to the scattering coefficient of correspondent alumina particles cloud is higher than that of aluminum particles cloud while the absorption coefficients of them are comparable.For the scattering phase function of alumina/aluminum particles cloud,it is hardly affected by temperature and cap thickness ratio because the transition of scattering regime mainly depends on the size parameter.

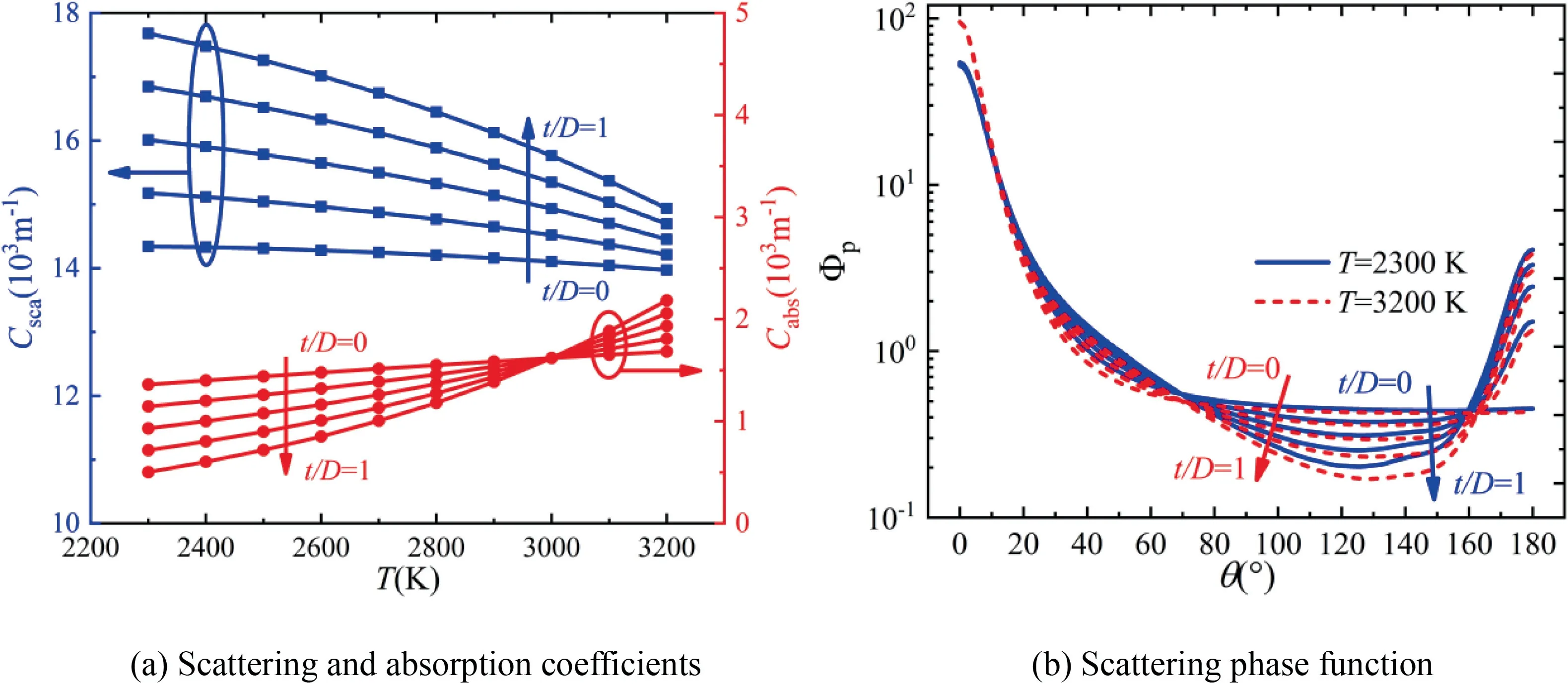
Fig.20 Effective gray radiative properties of alumina/aluminum particles cloud for Distribution A.

As shown in Fig.21,the effective gray radiative properties of alumina/aluminum particles cloud with different cap thickness ratios () are obtained at different temperatures for diameter Distribution B.Both the scattering and absorption coefficient increases with temperature.With the increase of cap thickness ratio,Both the scattering and absorption coefficient decreases.The explanation of these two trends is similar to that of Distribution A.As the cap thickness ratio increases,the scattering phase function varies slightly at different temperature and the explanation is already made in last paragraph.

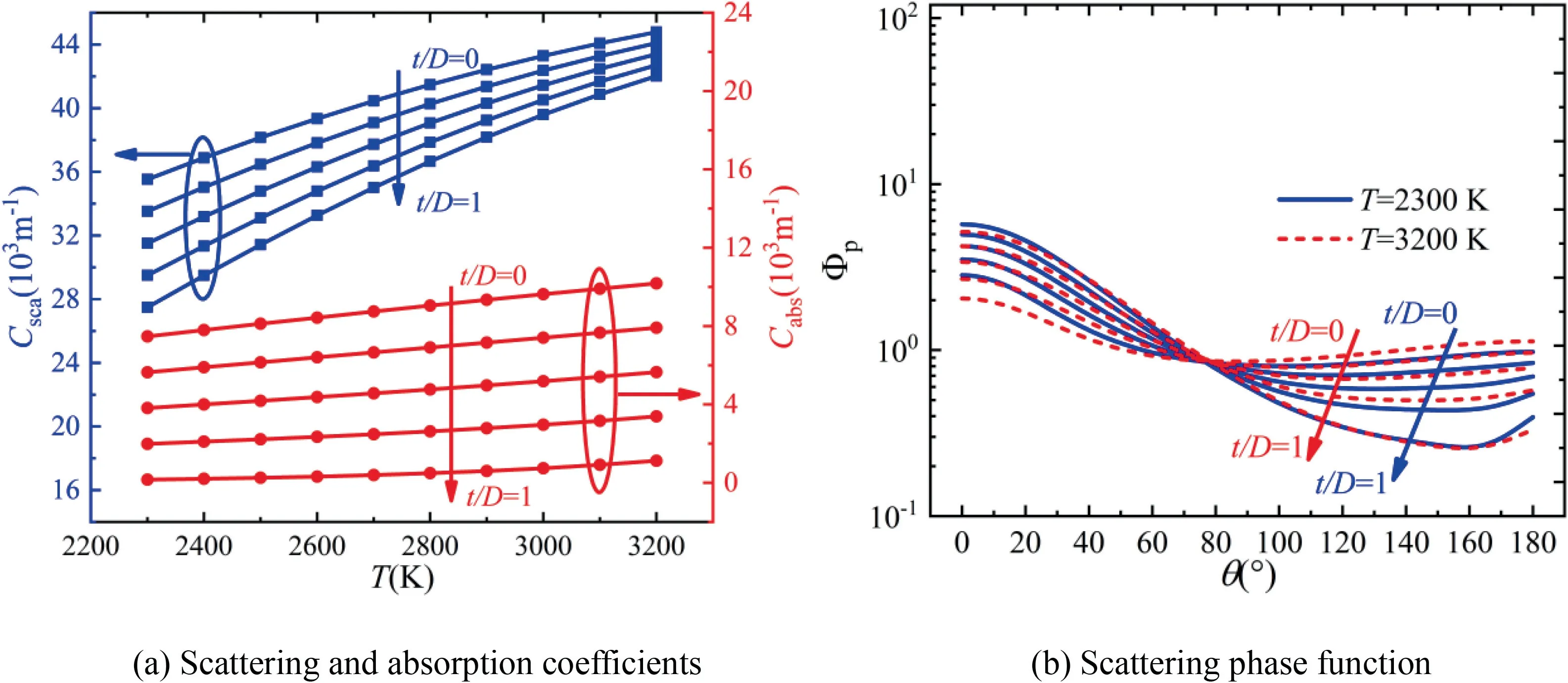
Fig.21 Effective gray radiative properties of alumina/aluminum particles cloud for Distribution B.

In sum,the variations of effective gray radiative properties of alumina/aluminum particles cloud are very similar to that of alumina particles cloud and aluminum particles cloud because the variations of effective gray radiative properties of alumina particles cloud and aluminum particles cloud are also very similar.

3.3.Thermal environment inside the motor

The total,radiative and convective heat flux distributions along the wall inside the motor (head,burning surface and nozzle wall) are obtained as shown in Fig.22.In this figure,is the heat flux andis the length of the path along the arrow.At the head section (Section 1 in Fig.22),the convective heat flux decreases sharply as the position closes to the burning surface (Section 2),and then remains at a very small value.On the contrary,the radiative heat flux accounts for the vast majority of the total heat flux and decreases firstly and then increases along the Line 1 direction at the head section.At Section 2 and Section 3 (i.e.the side-burning and end-burning surfaces),the convective heat flux is not calculated because these sections are set as the inlet boundary condition.But we can still conclude that the convective heat flux within these two sections is relatively small from the magnitude of convective heat flux at the adjacent sections,which is attributed to the small gas velocity in this region.The radiative heat flux at Section 2 and Section 3 reaches as high as 5.6(Section 2)-6.8 (Section 3) MW/mrespectively and dominates the heat transfer process since the burning surface has the highest temperature.At Section 4 (i.e.the wall of nozzle),the convective heat flux increases rapidly in the converging section due to the acceleration of gas flow,reaches the peak value of 11.2 MW/mnear the throat,and then decreases rapidly in the diverging section due to the sharp drop of temperature and pressure.For the radiative heat flux at nozzle,since the temperatures of gas phase and particle decrease rapidly after the throat,in addition,the particles accelerate rapidly and become sparse in the downstream of the nozzle,the radiative heat flux is reduced drastically.In general,the heat transfer in the combustion chamber is dominated by thermal radiation due to the high temperature and low velocity of gas and particles,while in the nozzle the influence of thermal radiation gradually attenuates and the convective heat transfer plays a dominant role due to the increment of velocity of gas and particles.

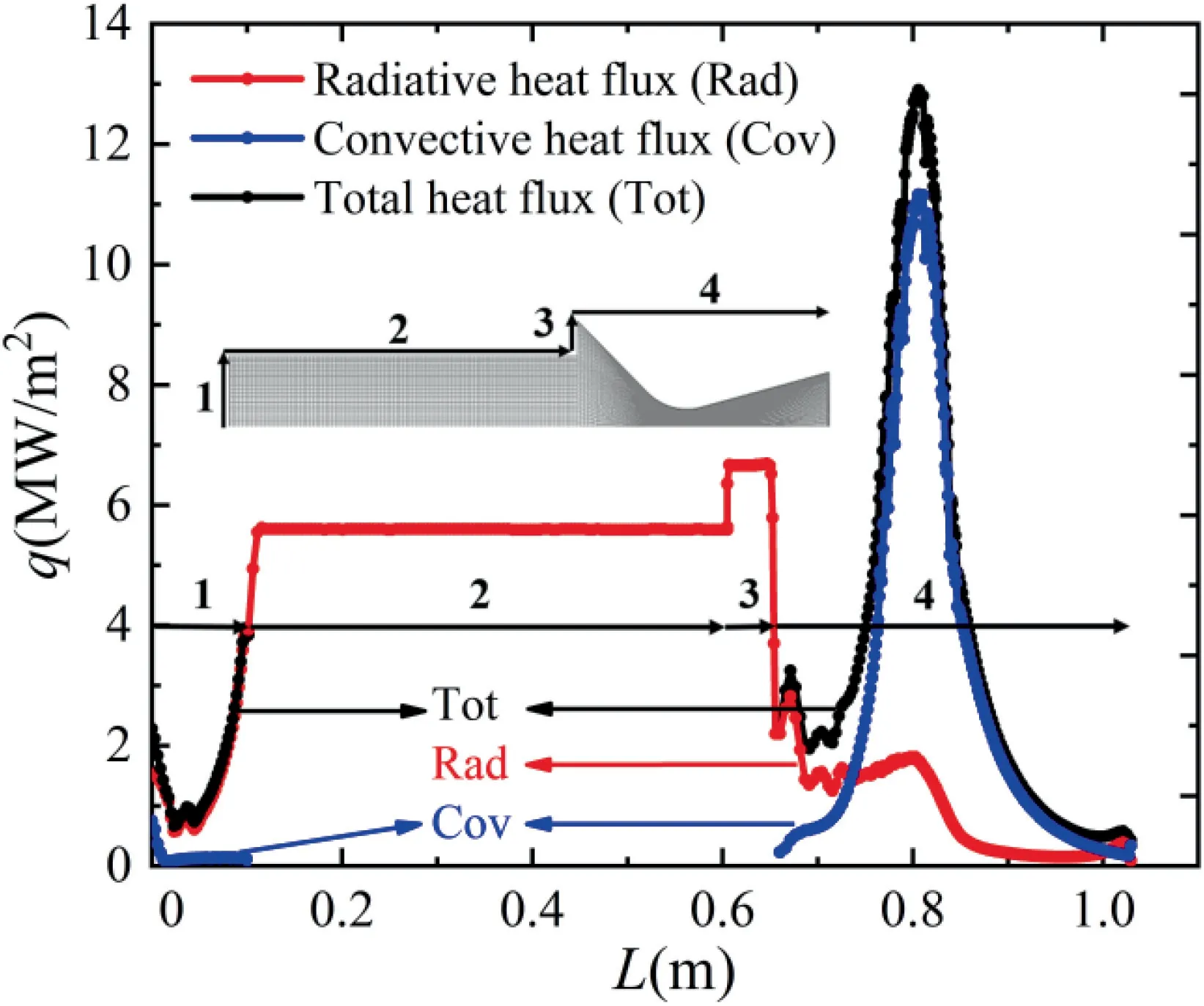
Fig.22 Heat flux distribution along wall.

The distributions of convective and radiative heat fluxes in the combustion chamber (Sections 1 and 2) can be explained by Figs.23 and 24.For the convective heat flux,it starts with a high value that caused by the enhancement of convective heat transfer by the recirculation zone formed near the middle of the motor head(marked and zoomed locally in Fig.23)and remains at a very small value later due to the relative small velocity of gas and particles near the side burning surface.For the radiative heat flux at Section 1,its variation can be explained by the distributions of absorption coefficient and scattering coefficient near the head section in Fig.24.The absorption coefficient in the region corresponds to Circle 4 and Circle 1 in Fig.24 is relatively large (i.e.particle emission is also very strong) and the scattering coefficient of that is relatively small.From the axis to the burning surface,the absorption coefficient decreases firstly and then increase.Meanwhile,the scattering coefficient within Circle 2 is much larger than that within Circle 1.Thus,the radiative heat flux of the head near Circle 5 has the minimum value.When approaching to the side burning surface,the absorption coefficient rises again(corresponding to the region of Circle 6)and the thermal radiation from the burning surface with higher temperature is enhanced.As a result,the radiative heat flux at the head increases to the value as the same as the burning surface.At Section 2,due to the low velocity of particles near the sideburning and end-burning surfaces,the number density and optical thickness are very large.Therefore,the heat flux of burning surface is determined by the radiative properties of particles cloud near two burning surfaces (optically thick approximation),and the radiative heat flux remains essentially unchanged along two burning surfaces.

Fig.23 Streamlines in motor (right) and local vector of velocity (left).

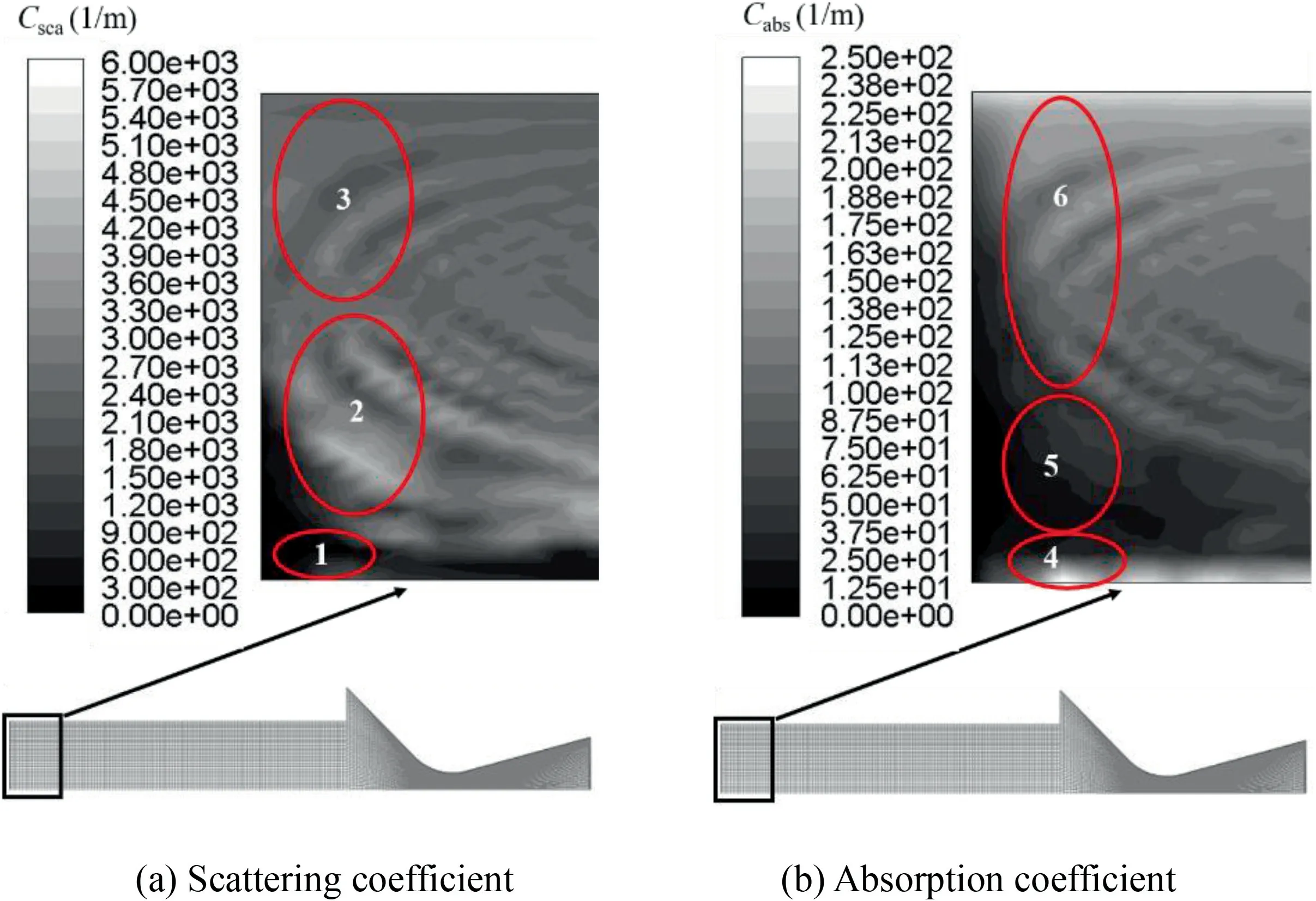
Fig.24 Distributions of scattering and absorption coefficients near motor head.

3.4.Influence of alumina/aluminum particles

The influence of the ratio of alumina/aluminum particles on the radiative heat flux along the wall is studied and compared in Fig.25.As the combustion efficiency of aluminum (η)reduces from 100% to 80%,the radiative heat flux at most inner surfaces of the motor remains unchanged.However,the radiative heat flux at the diverging section of the nozzle increases slightly with the decrease of combustion efficiency.

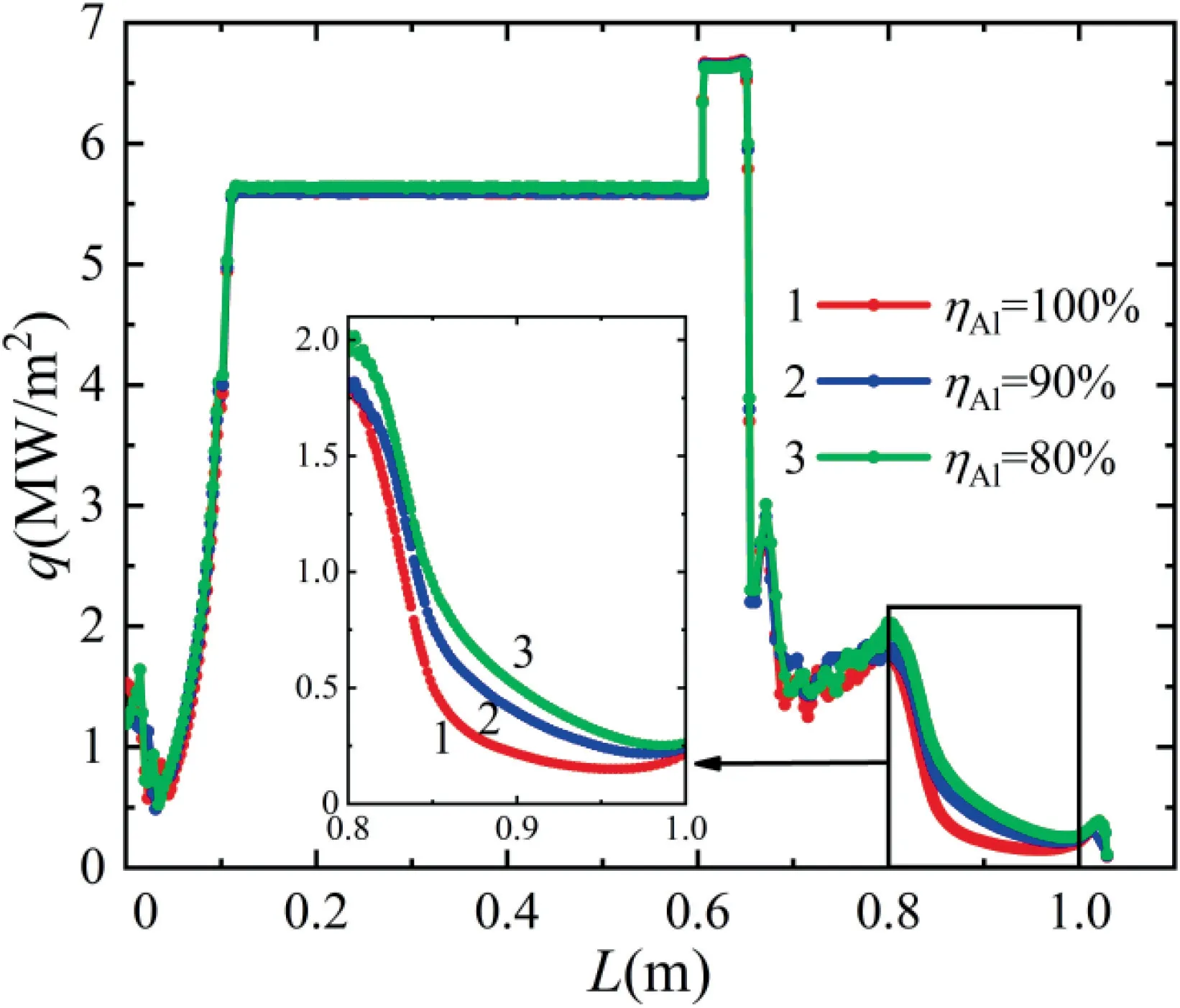
Fig.25 Radiative heat flux along wall at different combustion efficiency.

The phenomenon can be explained from Fig.26.The alumina/aluminum particles with diameter of 1.2 μm account for the majority of the mass flow.Its absorption efficiency(i.e.particle emission) at high temperature (≥3400 K) has much less variation than that at low temperature as the combustion efficiency of aluminum drops from 100% (solid lines)to 80%(dashed lines).In addition,the calculated temperature near the burning surfaces and the converging section is also as high as 3400 K.As a result,the radiative heat flux remains essentially unchanged before the throat of the nozzle.In the diverging section of the nozzle (low temperature region),the absorption efficiency increases as the combustion efficiency decreases and the scattering efficiency decreases slightly (maximum deviation ≤6% within 2300-3800 K).Meanwhile,the typical temperature calculated in the diverging section of the nozzle is about 2000 K.Therefore,the radiative heat flux at the diverging section wall increases with the decrease of combustion efficiency.

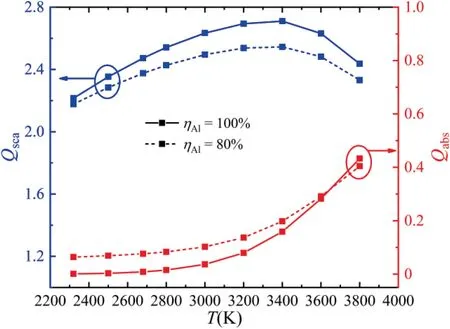
Fig.26 Radiative properties of alumina/aluminum particles with diameter of 1.2 μm at different combustion efficiency.

4.Conclusions

In this paper,the radiative properties of an individual alumina,aluminum and alumina/aluminum particles and their corresponding cloud are calculated.With considering the influence of particle radiation,the thermal environment of a subscale SRM is investigated numerically.The main findings of this study is as follows.

(1) A multiscale method with considering the radiation of condensed phase particles is established to predict the thermal environment inside SRMs.At microscale,the effective gray radiative properties of individual particles(alumina,aluminum,and especially alumina/aluminum)and corresponding particles cloud are calculated using Mie theory and an approximate method.The radiative properties of particles are incorporated with the twophase flow and heat transfer simulation within SRMs to predict its thermal environment at macroscale.

(2) For the individual alumina,aluminum,and alumina/aluminum particles,with the increase of diameter,the scattering efficiency reaches to its peak at about 1 μm and then decreases,while the scattering phase function transits from isotropic to anisotropic.However,the absorption efficiency of aluminum particle increases to the maximum at～0.4 μm and then decreases while the absorption efficiencies of alumina and alumina/aluminum particles maintain the same increasing trend with diameter.As the temperature increases,the absorption efficiencies of alumina,aluminum,and alumina/aluminum particles generally increasing.Meanwhile,the scattering efficiency increases with temperature at small diameter and decreases at large diameter.The scattering phase function of the three types of particles remains essentially unchanged with temperature.With the increment of cap thickness ratio (),the scattering phase function is basically unchanged while the variation of scattering efficiency and absorption efficiency is complex and depend on the temperature and particle diameter.

(3) For the particle cloud,the variation of radiative properties with temperature is basically similar to the numerically dominant particles.The scattering coefficient of alumina,aluminum,and alumina/aluminum particles cloud increases with temperature for Distribution A,but decreases for Distribution B.However,their absorption coefficients increase with temperature for both distributions while the scattering phase function is essentially invariant with temperature and more isotropic for Distribution B.As the cap thickness ratio ()increases,the scattering phase function varied slightly and the scattering coefficient increases continuously while the absorption coefficient decreases at low temperature and increases at temperature higher than 3000 K for Distribution A.For Distribution B,the scattering phase function has small variation with the cap thickness ratio,and the scattering coefficient increases while the absorption coefficient decreases with the cap thickness ratio.

(4) The calculated radiative and convective heat flux distributions along the wall inside the 75-lb BATES motor indicate that heat transfer in the combustion chamber is dominated by thermal radiation and the radiative heat flux at the chamber surface is essentially a constant about 5.6-6.8 MW/m.On the contrary,the convective heat transfer plays the dominant role in the nozzle and the convective heat flux increased to 11.2 MW/mnear the throat.As the combustion efficiency of aluminum drops (more aluminum),the radiative heat flux in the vast majority of the motor remains essentially unchanged,but increases slightly along the diverging section wall of the nozzle.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

This work was supported by the Innovative Talents Support Plan of China Postdoctoral Foundation (No.BX20180244),National Natural Science Foundation of China (No.51825604) and the Fundamental Research Funds for the Central Universities of China (No.xjj2018029).