组合GNSS观测值反演海面高度
王 洁,王娜子,徐天河,高 凡,贺匀峤
1. 山东大学空间科学研究院,山东 威海 264209; 2. 长安大学地质工程与测绘学院,陕西 西安 710000; 3. 中国科学院精密测量科学与技术创新研究院大地测量与地球动力学国家重点试验室,湖北 武汉 430077
监测和研究海面高度变化对沿海地区的自然环境、生态系统和经济发展等均具有重要意义[1]。传统的海面测高手段为验潮站和卫星测高,但验潮站数据易受地面沉降影响,而卫星测高数据在沿海岸地区精度较低[2]。GNSS-IR技术以其成本低、信号源丰富、可实现全天时和全天候观测等优点[3],可为沿海岸地区提供长期、高精度、不受地面沉降影响的海面高监测数据。其中,架设在海岸边的大地测量型GNSS设备获取的低仰角下的直射信号和经海面反射的多路径信号在接收机内部产生的干涉效应,影响了GNSS的码相位、载波相位及信噪比(SNR)观测值[4-7],这一效应与天线到海面的高度有关,因此可以利用GNSS-IR观测量进行测高反演研究。
GNSS-IR海面测高中最常用的观测量为SNR。文献[8]利用两个GPS观测站的SNR数据实现了海面高度反演,与附近的验潮数据相比,二者互差的均方根(RMS)在厘米级,且相关系数都优于0.97。文献[9]处理了位于阿拉斯加Kachemak海湾的GPS观测站1 a的SNR数据,获取的日平均海面高度与实地观测值互差的RMS为2.3 cm。文献[10]分析了5个GNSS观测站的SNR数据,反演得到的海面高度与验潮站结果相比,相关系数均优于0.89。文献[11]分析了OSO观测站的GPS和GLONASS多频点的SNR信号,获取了厘米级的海面高度反演结果。文献[12]利用SC02观测站的实测SNR数据对潮位变化监测进行了反演分析,与验潮站数据对比,两值较差约为10 cm,相关系数均优于0.98。文献[13]采用了非线性最小二乘方法分析两个GNSS站的SNR数据,与当地验潮站结果相比,瑞士Onsala站的海面测高结果标准偏差为1.4 cm,塔斯马尼亚州的斯普林湾站的海面高度偏差为3.1 cm。文献[14]采用了架设在海边的GNSS观测站10 a的SNR观测数据,反演得到了厘米级海面高度。文献[15—16]采用小波分析的方法分析了GNSS站的SNR数据,获取了分米级的海面高反演结果。文献[17]采用卡尔曼滤波方法分了GNSS观测站(GIGU站和SPBY站)的SNR数据,获取了实时的厘米级海面高度测量结果。文献[2]利用OSO观测站2015至2016年的GPS L1-C/A SNR数据,比对了多家单位基于GNSS-IR技术获取的海面高数据,结果表明海面高反演值之间具有很好的一致性,RMSE小于5 cm,相关系数大于0.9。
综上所述,SNR是较为成熟的GNSS-IR观测量,但是很多GNSS观测文件中并不包含这一类观测量,尤其是早期GNSS设备的输出文件。因此,考虑到利用早期观测数据进行海面高度长期变化研究的需要,寻求可替代的GNSS-IR观测量也是必要的。值得庆幸的是,码伪距和载波相位观测值也包含了GNSS-IR测高信息。文献[18]采用了以下BDS的3种观测值实现了海面高度反演:单频SNR观测值,三频载波相位的组合,以及三频码伪距的组合。利用这3种观测值/组合反演得到的海面高度,与验潮站数据对比相关系数为0.83~0.91。文献[19]利用SC02站的GNSS双频载波相位组合和SNR观测值反演了海面高度,与验潮站实测数据对比,相关系数均优于0.97。相对于文献中采用的双频和三频观测值,单频观测值组合更易实现。因此,本文首先引入单频伪距和单频载波相位组合的方法来实现GNSS-IR测高。但在该种组合方法中,为获取多路径误差部分,电离层延迟项需要先通过低通滤波器等方式去除。而未被去除的电离层延迟残差势必会影响海面高度反演精度。本文通过模拟证明了电离层残差对海面高度反演的精度存在一定的影响。因此,考虑到电离层残差会影响该组合反演海面高的精度,又引入了伪距和双频载波相位组合的方法,该组合为无几何无电离层组合,可避免电离层残差对反演结果的影响。为验证这两种GNSS观测值组合方法在海面高度反演方面的有效性,本文开展了岸基试验对上述组合方法进行验证分析,并与先前利用GNSS SNR观测值、双频载波相位组合和三频载波相位组合方法反演的海面高度进行比较。新组合方法的引入,进一步提升了GNSS-IR测高的适用范围。
1 码伪距和载波相位组合反演海面高度的原理
GNSS-IR反演海面高度原理如图1所示,通过对架设在海边的GNSS接收机中的反射信号部分进行分析处理可得到接收机天线相位中心至海面的垂直距离h(又称为反射面高度),而接收机天线的大地高(H)可通过精密单点定位(PPP)技术获取,因此,将接收机天线大地高(H)减h即可获得海面相对于椭球面的高度(hsea_level),计算如式(1)所示
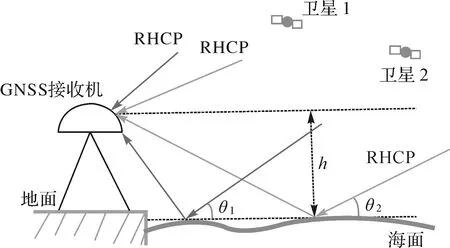
图1 GNSS-IR海面高度反演原理Fig.1 The principle of GNSS-IR sea level estimation
hsea_level=H-h
(1)
由式(1)可知,通过GNSS-IR技术实现海面高度反演的重点在于反射面高度h的准确确定。本文引入了基于GNSS码伪距和载波相位观测量的两种组合方式来实现反射面高度的计算,具体原理如下。
1.1 码伪距和单频载波相位观测值组合反演海面高原理
1.1.1 组合值反演海面高度原理
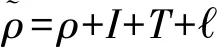
(2)
L=ρ-I+T+β
(3)
式中,ρ表示卫星到接收机之间的理论距离;I为GNSS信号在传播路径中所受电离层延迟的影响;T为传播路径中对流层延迟的影响。码伪距多路径误差和载波相位多路径误差β表示为[21-22]
(4)
(5)
(6)
式中,Δ(t)为反射信号相对于直射信号的路径延迟;振幅衰减因子α为接收的合成信号中反射信号振幅与直射信号振幅的比值;δφ为反射信号相对于直射信号的相位延迟;λ为载波波长。由式(6)可知,相位延迟δφ与卫星高度角正弦值(sinθ)存在函数关系。
则由式(2)、式(3)可得,码伪距和单频载波相位观测值的线性组合为
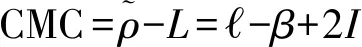
(7)
由式(7)可知,该组合受到电离层延迟影响。但由于电离层延迟的频率比多路径误差频率更低[7],因此可采用低通滤波法(本文采用移动平均滤波法)去除电离层延迟影响,由此可得码伪距和载波相位组合为
M(t)=(t)-β(t)
(8)
将式(4)、式(5)代入式(8)可得
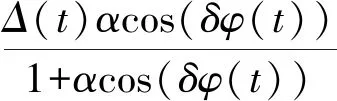
(9)
文献[6]指出,多路径引起的载波相位误差β(t)和码伪距误差(t)是具有相同峰值频率的变振幅正弦函数,该正弦函数是相对于变量sinθ的。通过近似化简,结合式(6)及式(9)可知,M(t)可看作是相对于变量sinθ的多个变振幅的正余弦函数的叠加,余弦函数的频率部分都是4πh/λ。这些结论也可通过图2看出。图2为简单选取α=0.1时,在不同的反射面高度下,结合式(4)、式(5)和式(8)模拟得到载波相位误差、码伪距误差和组合后的误差序列。由图2可以看出,载波多路径误差比伪距多路径误差小至少一个量级,因此,采用式(8)进行组合后的多路径误差与伪距多路径误差在反射面高度大于1 m时近似相等。即式(8)所表示的组合中用来进行海面高度反演的是伪距多路径误差,而载波相位观测值只是用来消除组合中的路径ρ、对流层延迟T和噪声等以实现孤立观测值中多路径部分的目的,且组合后仍存在电离层延迟,需要通过低通滤波器等方法去除。
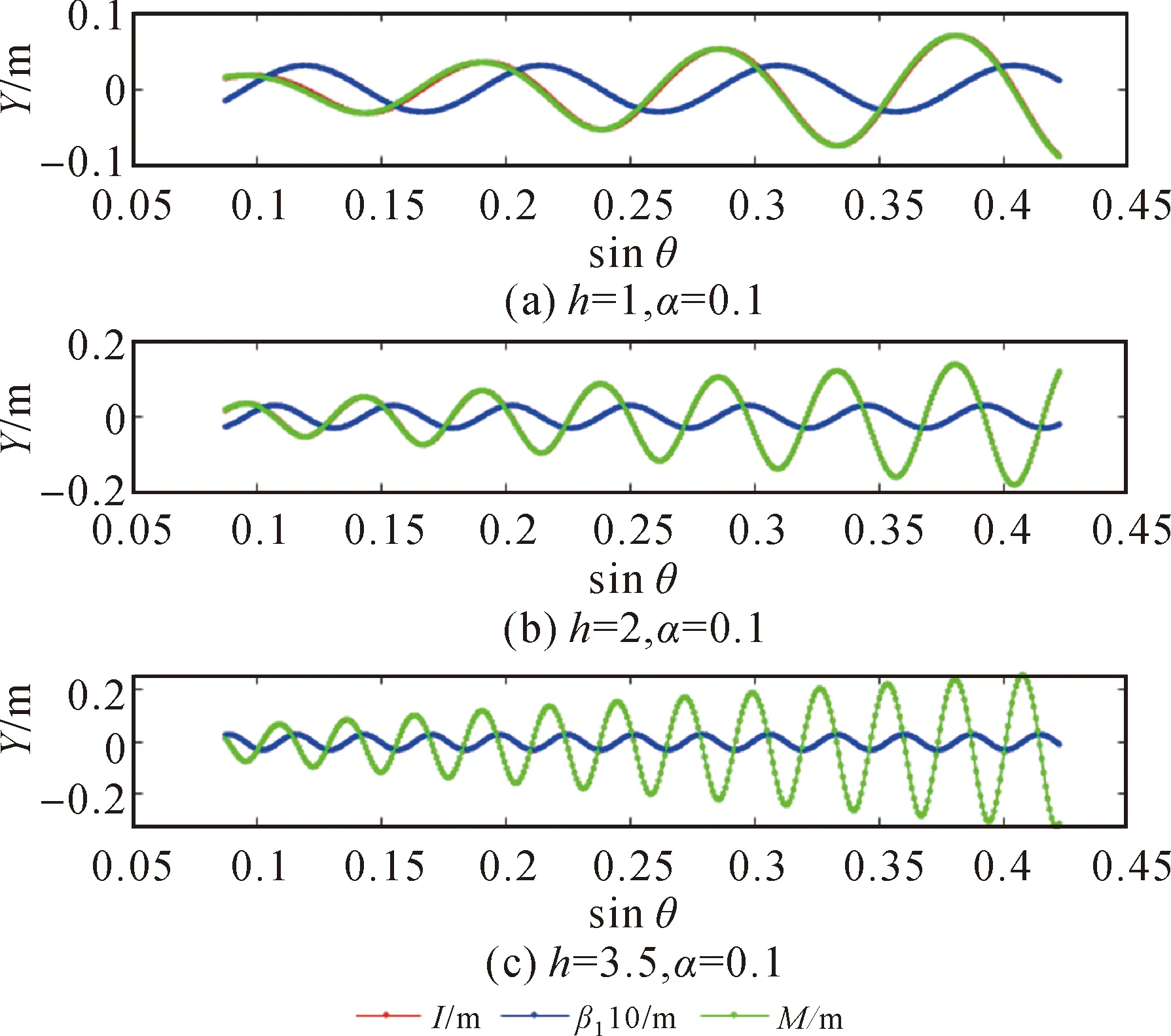
图2 不同反射面高度下模拟的伪距多径误差、载波多路径误差和组合后的多路径误差序列Fig.2 Multipath-induced pseudroange error, phase error and combined error oscillates with the sine of elevation angle
若对M(t)进行频谱分析(考虑到M(t)相对于sinθ是非间隔采样,频谱分析方法常用Lomb-Scargle Periodogram[23]),则可得谱峰值频率[4]
(10)
由上述分析可知,通过对观测值M(t)序列进行谱分析得到峰值频率f,则可得由式(10)得出反射面高度h。
图3(a)为实测的BDS C21卫星的M(t)观测序列,对M(t)频谱分析(如图3(b)所示)即可得谱峰值频率,再由式(10)计算反射面高度h,最后代入式(1),即可得海面高度值。
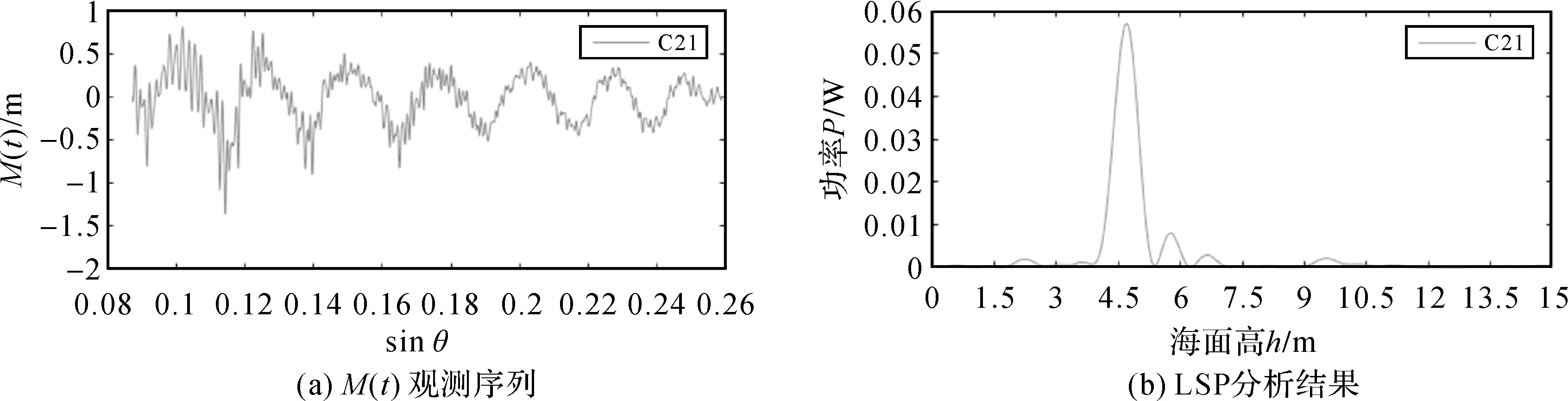
图3 BDS C21卫星M(t)观测序列及其对应的LSP分析结果Fig.3 M(t) observation sequence of BDS C21 satellite and its corresponding LSP analysis results
1.1.2 电离层延迟误差对GNSS-IR海面高度反演结果的影响
在式(7)中,利用GNSS组合值反演地表参数时,为得到多路径组合值,需要先去除其中的电离层延迟项。考虑到电离层延迟的频率小于0.1 MHz,而谱分析后的多路径误差的频率在1 MHz至几十MHz之间,常采用低通滤波器的方式来去除电离层延迟的影响[7,24]。大部分文献采用10阶多项式拟合实现低通滤波以去除电离层延迟的影响[19,22]。也有采用更高阶多项式或者别的低通滤波方法来实现此步骤,如文献[5]利用14阶多项式拟合作为低通滤波以去除电离层延迟和噪声的影响。文献[7]利用滑动均值滤波去除单频载波相位与伪距组合中的电离层延迟影响,以实现积雪厚度的反演。这些方法已成功应用于基于观测值组合的GNSS-IR地面特征反演中,但受低通滤波方法的限制和噪声的影响等,利用这些方法并不能完全去除组合值中的电离层延迟,导致组合值中存在有一定的电离层延迟残差,最终会影响海面高度反演的精度。下文将证明这一结论。但考虑到当前利用GNSS-IR实测数据反演的海面高度结果受多种因素的联合影响(如文献[25]所讨论的噪声、动态海面、观测值采样率、反射面高度等),导致反演精度较低,无法单独讨论电离层延迟残差项的影响,因此,采用模拟数据对该项误差进行研究。
SC02站(48.5°N,123°E)是GNSS-IR研究的常用观测站[12,14,19]。该站处于中纬度地区,相对于高纬度和低纬度地区测站,其受电离层影响稍弱。若此站所受电离层延迟残差会影响GNSS-IR海面高度反演精度,则处于高纬度和低纬度地区的其他站也会受到该类误差影响。因此本文选取该站作为模拟的参考站。为保障多路径数据来自海面反射,选取该站的高度角范围为5°~15°,方位角范围为50°~240°。具体的模拟步骤如下:
(1) 结合GPS精密星历和站点位置,考虑到高度角和方位角范围,获取反射点落在海面的多颗卫星的多条弧段。
(2) 利用附近验潮站数据和该天的平均反射面高度计算(1)中各个弧段对应的反射面高度。
(3) 将(2)所得反射面高度、对应弧段的最大和最小高度角以及方位角作为输入值,并设定反射面为水面和接收天线类型,利用文献[26]所提供的程序模拟单频伪距和载波相位组合多路径序列M(t),该序列(如图4(a)中虚线序列所示)中不包含电离层延迟的影响。
(4) 利用IGS提供的当天的电离层Map图以及双线性插值法,计算上述多路径序列中采样点的电离层延迟值dE(t)。
(5) 利用CMC(t)=M(t)+2dE(t)(同式(7))计算得到加入电离层延迟后的组合值序列(如图4(a)所示)。
(6) 采用低通滤波器(如10阶多项式拟合)去除模拟CMC(t)中的电离层延迟项,得到dCMC(t)(图4(b)所示)。
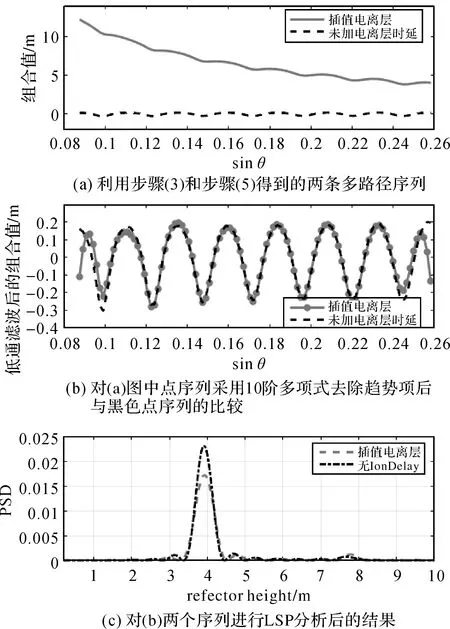
图4 模拟过程中的一条卫星多路径弧段示例Fig.4 An example of simulated multipath oscillating series in simulation process
(7) 分别对M(t)和dCMC(t)进行LSP分析,利用峰值频率,经式(10)计算得到两种情况下的反射面高度。这两种反射面高度值之间的差值,即为低通滤波器未去除的电离层延迟残差对海面高度反演所造成的影响。
利用上述步骤对SC02测站实现了2013年9月24日GPS卫星L1信号的数据模拟,模拟结果如图5所示。由图5(b)可以看出,模拟得到的反射面高度与验潮站数据具有较好的一致性。但由图5(a)可以看出:采用低通滤波器(此处是10阶多项式拟合法)去除电离层延迟后得到的反射面高度与不存在电离层延迟时得到的反射面高度并不相等,这说明低通滤波器并没有完全去除组合值中的电离层延迟,在组合值中仍存在有电离层延迟残差。且该残差造成的反射面高度的差异分布于[-2,6] cm范围内。经计算,该天反射面高度差异的RMS为1.9 cm。SC02站位于中纬度地区,而受电离层影响更大的高纬度和低纬度的测站,电离层残差造成的反射面高度的差异可能分布于更大的范围内,且反射面高度差异的RMS也更大。
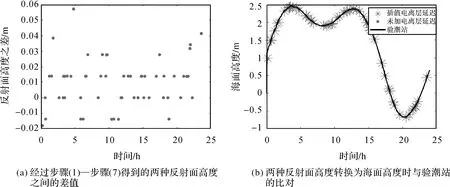
图5 利用SC02测站2013年9月24日GPS卫星L1信号模拟得到的结果Fig.5 One-day results from the simulated GPS L1 signals at SC02 station on September 24, 2013
由此可见,在利用单频伪距和载波相位组合值进行海面高度反演时,虽采用了低通滤波器去除电离层延迟的影响,但未被低通滤波器去除的电离层延迟残差对海面高度反演的影响仍是不容忽视的。因此,下文引入另一种组合方式来实现海面高度反演。该组合通过观测量之间的加减运算直接消除电离层延迟误差,可以避免1.1.1节中组合值经低通滤波后电离层误差的存在对反演结果精度产生的影响。
1.2 码伪距和双频载波相位观测值组合反演海面高原理
为消除1.1节所述组合中电离层延迟的影响,可将码伪距和双频载波相位观测值组成无几何无电离层组合[9]
(11)
系数为
(12)
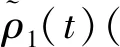
M2(t)=1(t)+κ1β1(t)+κ2β2(t)
(13)
同前述码伪距和单频载波相位观测值组合反演海面高原理,通过近似化简,综合式(4)、式(5)、式(6)、式(13)可知,M2(t)也可看作是多个具有相同相位δφ(t)的变振幅正弦函数的叠加。不同的是该组合包含两个频率的信号。由图2及文献[26]可知,码相位多路径误差值大小是载波相位多路径误差的近10倍,因此,在式(13)中,频率2信号部分在M2(t)中相对频率1信号值较小,对M2(t)进行谱分析,可近似认为较为明显的峰值频率是相对于频率1的。该结论也可由图6得出。图6为简单选取α=0.1时,在不同的反射面高度下,利用式(4)、式(5)和式(13)模拟得到码伪距误差l(t)、κ1β1(t)+κ2β2(t)和组合后的误差序列M2(t)。由图6可以看出,伪距多路径误差决定了组合后的多路径误差的频率和振幅。即式(13)所表示的组合中用来进行海面高度反演的仍然是频率1的伪距多路径误差,组合中加入的双频载波相位观测值只是用来消除路径ρ、对流层延迟T、电离层延迟I和噪声等以实现孤立观测值中多路径部分的目的。则可根据频谱分析所得峰值频率和频率1的波长,由式(10)计算反射面高度,再由式(1)计算海面高度。
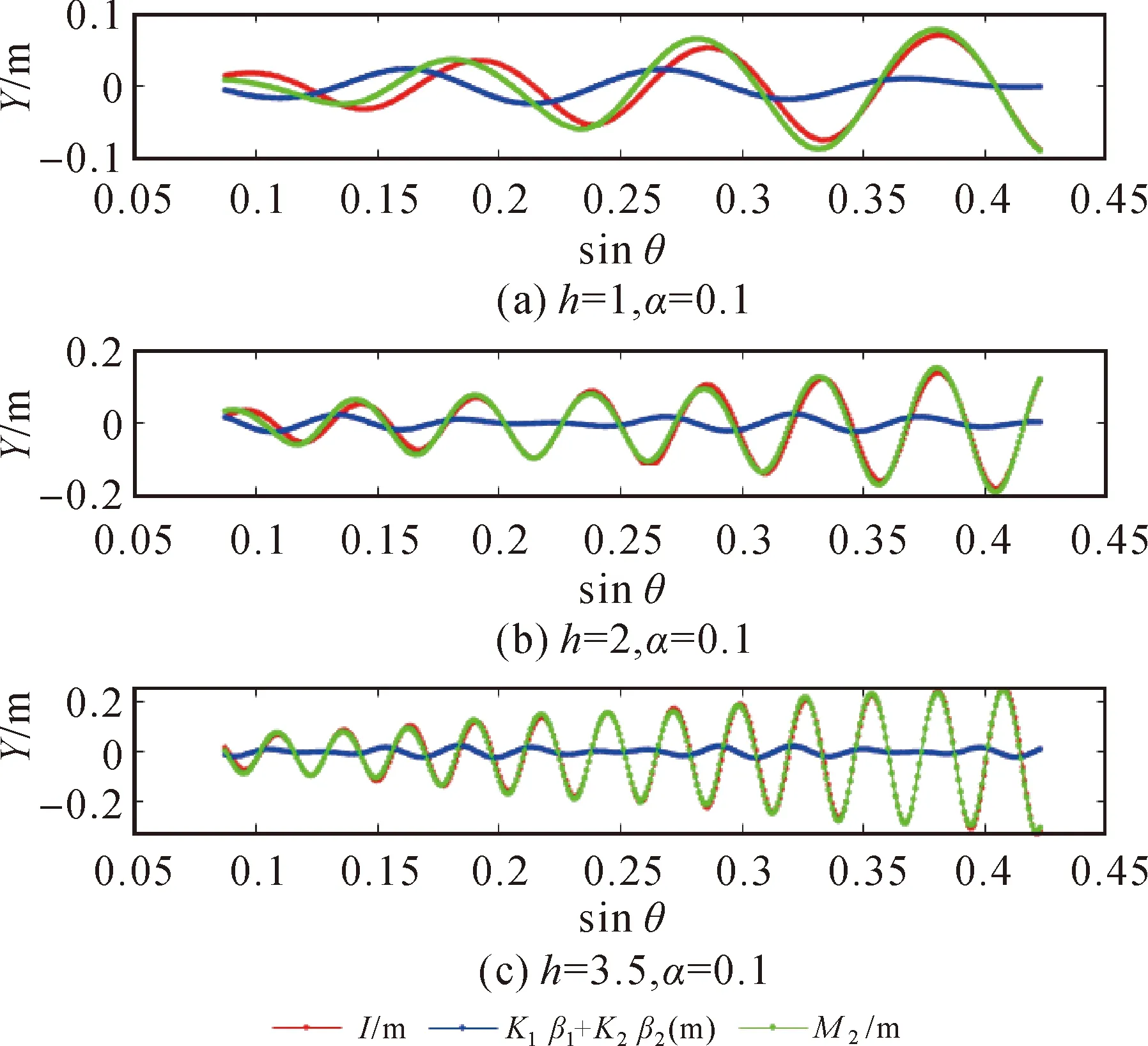
图6 不同反射面高度下模拟得到的码伪距误差l(t)、κ1β1(t)+κ2β2(t)和组合后的误差序列M2(t)Fig.6 Multipath-induced pseudroange error l(t), κ1β1(t)+κ2β2(t) and combined error M2(t) oscillates with the sine of elevation angle when the antenna height is different values are tested, respectively
图7(a)所示为实测的BDS C33卫星M2(t)误差序列,对M2(t)误差序列进行频谱分析(图7(b))得出1个较为明显的谱峰值频率,再由式(10)和式(1)可计算反射面高度。
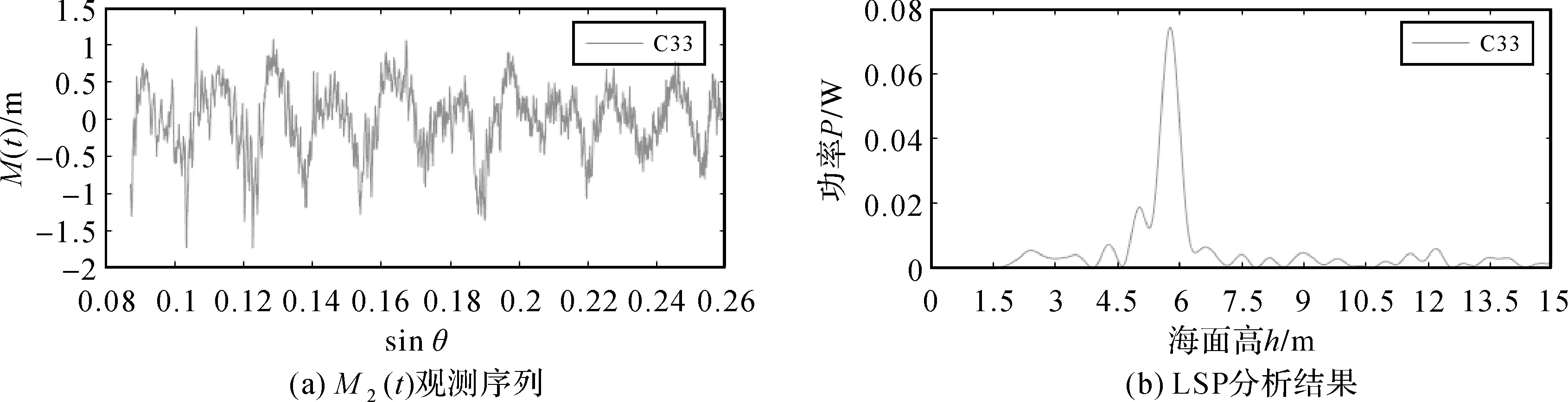
图7 BDS C33卫星M2(t)观测序列及其对应的LSP分析结果Fig.7 M2(t) bservation sequence of BDS C33 satellite and its corresponding LSP analysis results
2 试验与结果分析
2.1 试验概况
为验证上述两方法反演海面高度的可行性,在山东省某一海边栈桥(37.534 1°N,122.045 8°E)架设仪器采集GNSS观测数据,测站接收机采用多模多频GNSS接收机SeptentrioPolaRX5(如图8(a)所示),接收机采样速率为1 Hz。试验采集了2019年DOY 262—265的GPS和BDS卫星的观测数据,其中DOY 262由于观测环境影响缺失部分观测数据。GNSS接收机接收到的信号主要来源于第一菲涅尔反射区,图8(c)为利用文献[27]提供的GNSS-IR软件绘制的此测站基于GoogleEarth的视图中GPS L1波段的第一菲涅尔反射区。由图8可知当卫星高度角为5°~15°,方位角为190°~330°时,第一菲涅尔反射区位于开阔海域中,因此,本文试验选择在此高度角和方位角范围内的数据进行处理分析。具体如何选择最优的高度角和方位角范围,也可参考文献[28]。同时,在同地安置了时间分辨率为1 s、测高精度为3 mm的雷达高度计(如图8(b)所示),该仪器可测量海面至高度计的垂直距离。并在试验期间利用全站仪测得GNSS接收机至雷达高度计相位中心的垂直距离为2.4 m。

图8 测站概况Fig.8 Overview of the GNSS station
2.2 结果分析
利用上述两种方法运用此测站的GPS和BDS观测数据进行了海面高度反演,并与雷达高度计记录结果进行了对比分析。图9为上述基于GPS和BDS观测数据的两种反演方法计算的海面高度与雷达高度计实测海面高度关系图,由图可知,反演结果与雷达高度计实测数据具有良好的一致性:除利用BDS系统的C2I、L2I和L6I组合反演结果的相关系数为0.85外,利用两个系统其余信号组合得到的反演结果,与高度计数据相比,相关系数均大于0.90。图10为两种反演方法计算的海面高度与雷达高度计记录结果的互差值均在±0.5 m内,表明本文所述的组合方法均可用于海面高度的测量。
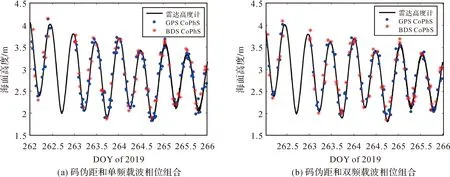
图9 利用不同观测值组合反演得到的海面高度值与雷达高度计数据比较Fig.9 Inversion of sea level estimation after combination of different observations
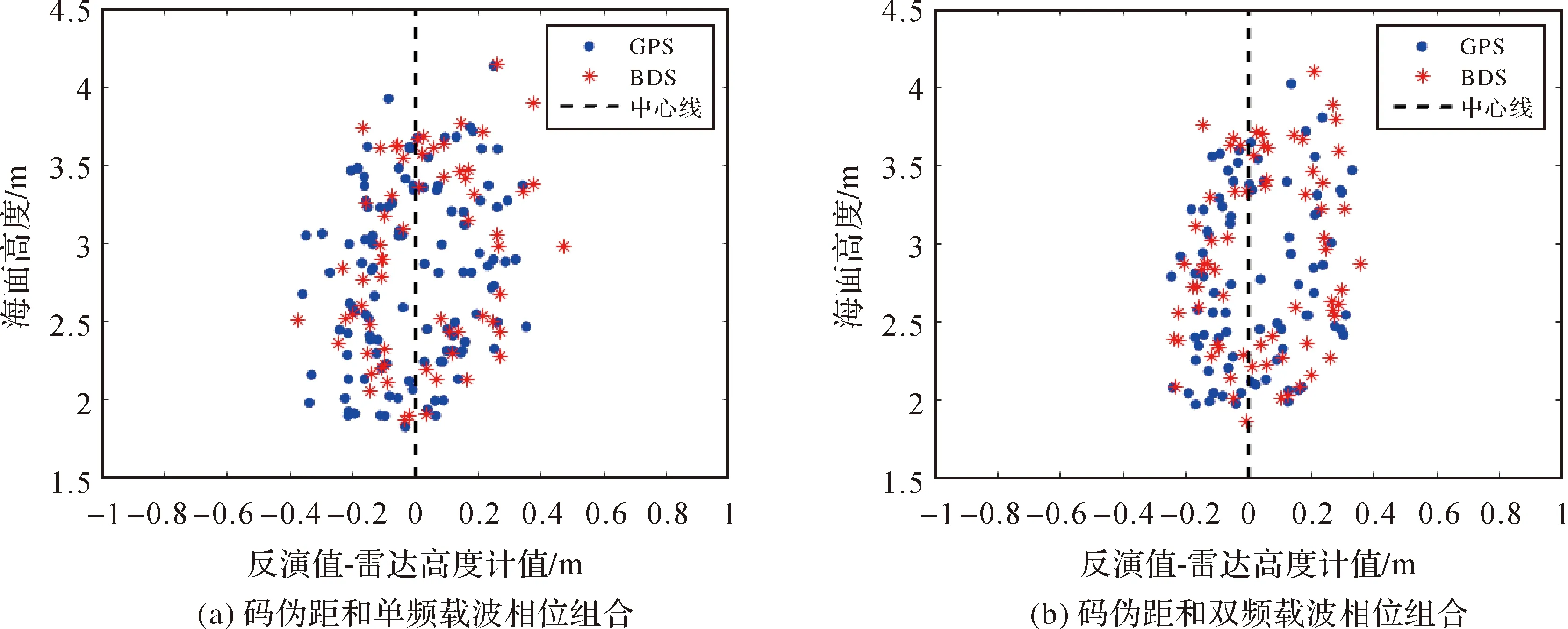
图10 测站海面高度反演值与雷达高度计值的互差Fig.10 The difference between the retrieved sea level estimation and the radar altimeter
表1和表2为基于GPS和BDS的码伪距和单频载波相位以及码伪距和双频载波相位组合反演值的精度统计结果,包括海面高度反演结果与雷达高度计数据的平均误差(mean)、均方根误差(RMSE)及相关系数,并在统计过程中采用3倍中误差剔除了反演值中的粗差。其中,BDS系统也利用了由BDS-2系统播发的卫星频率B2b(信号为C7I,L7I和S7I)进行计算,但该频率信号相对其他信号精度较差,卫星数目较少,因此,经由该信号反演得到的结果较差,表1、表2和表3中所有涉及该信号的组合(如组合C7I、L7I;组合C6I、L6I、L7I;组合L6I、L7I;组合L2I、L7I;组合C6I、L6I、L7I)反演得到的海面高度RMSE值都约为0.25 m,相对于其他组合精度较差。因此,在下述分析中,不考虑该信号的反演结果。
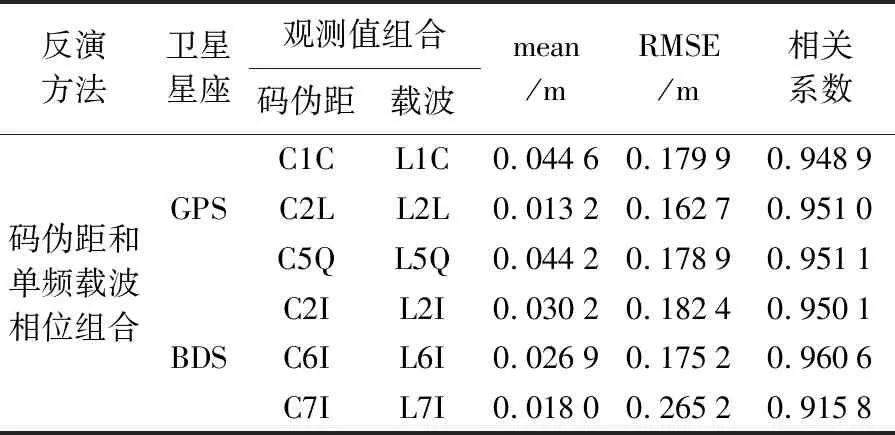
表1 GPS和BDS的码伪距和单频载波相位组合反演海面高度的精度统计Tab.1 Statistics of sea level estimation using GPS and BDS pseudorange and single-frequency carrier phase combination
由表1可以看出,利用码伪距和单频载波相位组合的方法实现的海面高度反演结果与雷达测高数据相比,GPS信号得到的海面高度RMSE为16~18 cm,BDS信号得到的海面高度RMSE为17~19 cm。由表2可以看出,利用码伪距和双频频载波相位结合的方法实现的海面高度反演结果与雷达测高数据相比,GPS信号得到的海面高度RMSE为15~19 cm,BDS信号得到的海面高度RMSE为17~19 cm。通过这两组数据可以看出,GPS信号比BDS信号反演得到的海面高度精度稍好。由式(7)可知,码伪距和单频载波组合中包含有电离层成分,一般需采用数据处理方法去除电离层延迟影响,但可能因为去除方法的不完美,组合值中仍可能有电离层延迟残差的存在,进而会影响海面高反演结果的精度。而码伪距和双频载波组合方法为无几何无电离层组合,不受电离层延迟残差的影响。因此,理论上前一种组合方法的海面高反演精度可能会低于后一种组合方法。但由表1和表2知,本文试验数据处理结果中,在GPS观测值的4个组合中,有3个组合由第2种方法反演得到的RMSE小于第1种方法;在BDS观测值中的3个组合中,1个组合利用后一种方法所得的反演精度与前一种方法相当,1个组合稍差,1个组合稍优。整体而言,两种组合的反演精度相当,电离层残差对反演结果精度的影响表现不明显,可能一方面是因为试验期间电离层相对稳定且数据处理时采用的移动平均滤波法去除电离层效果较好[7],另一方面是因为相对于当前分米级的测高精度,厘米级的电离层延迟残差改正对反演结果的影响并不能明显体现。
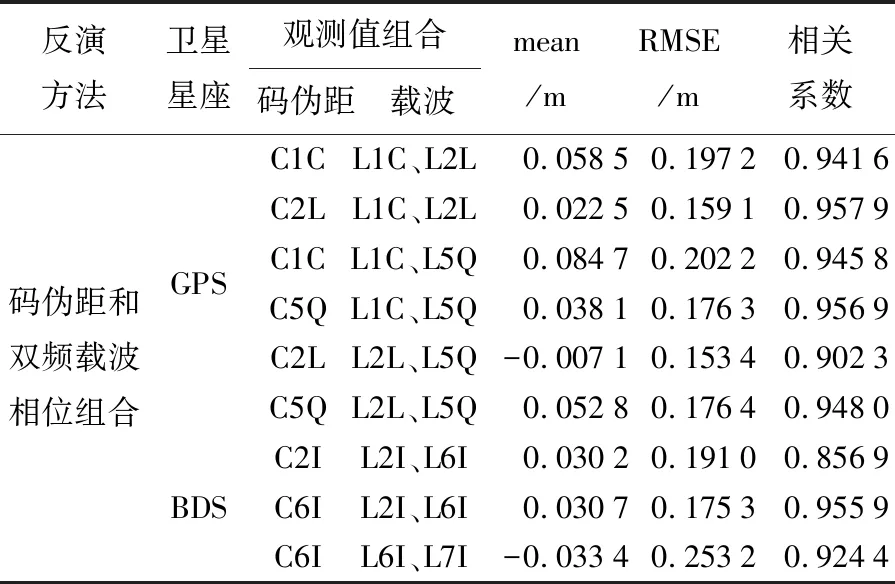
表2 GPS和BDS的码伪距和双频载波相位组合反演海面高度的精度统计Tab.2 Statistics of sea level estimation using GPS and BDS pseudorange and double-frequency carrier phase combination
同时,为进一步验证本文所述方法的可行性,作为对比,也分别利用SNR数据[8]、双频载波相位组合值[19]及三频载波相位组合值[18]计算得到了的海面高度与雷达测高计数据比较的统计结果,具体数值见表3。其中,SNR方法得到的海面高度RMSE为14~17 cm,双频载波相位组合方法得到的海面高度RMSE为15~19 cm,三频载波相位组合方法得到的海面高度RMSE为18~20 cm。本文方法得到的数据结果较单独使用SNR数据所得结果相比,精度稍差。主要原因在于:相较于码伪距和载波相位观测值,SNR值不用考虑电离层残差、周跳探测、整周模糊度等的影响,更易获取相对较为准确的海面高结果,这也是大部分GNSS-IR测高都是基于SNR数值进行计算的重要原因。但利用本文所述方法与利用双频和三频载波相位组合的方法所得海面高度精度相当,反演得到的海面高度RMSE都为15~20 cm。
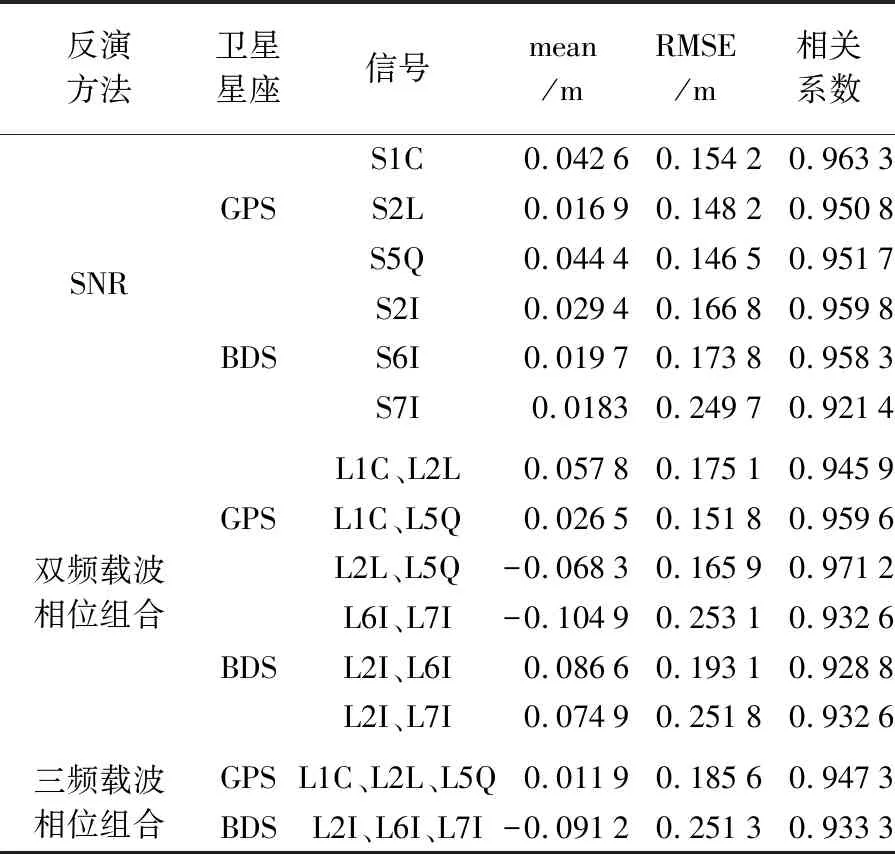
表3 SNR值反演海面高度、双频载波相位组合、三频载波相位组合反演海面高度的精度统计Tab.3 Statistics of sea level estimation based on SNR and different combinations
综上所述,文中所引入的两种组合方法都可实现海面高度反演,得到的海面高度精度与其他GNSS-IR测高方法相当,与雷达高度计数据相比,RMSE约为15~19 cm,相关系数均优于0.85。
3 讨论和结论
本文利用单频码伪距分别与单频载波相位和双频载波相位观测量的组合,成功实现了GNSS-IR测高反演,并利用外部高度信息进行了验证,结果显示本文所提的方法可行。同时,为进一步对比,也分析了基于SNR、双频载波相位组合、三频载波相位组合的GNSS-IR海面测高反演结果。结果表明:基于GPS和BDS的两种观测值组合,海面高度的反演结果与雷达高度计记录的结果显示较好的一致性,相关系数均优于0.85,除BDS B2b外,其余信号的海面高反演精度基本优于0.20 m。并且本文的两种方法得到的反演结果精度与已有方法得到的反演结果精度相当。因此,当观测文件中缺少SNR观测值时,可利用本文方法代替SNR观测值实现GNSS-IR海面高度反演。另外,在本文的两种方法中,考虑到电离层残差的存在,导致理论上码伪距和双频载波相位观测值的组合会优于码伪距和单频载波相位组合方法,但从试验结果看,GPS观测值的4个组合方式中有3个组合表现出了该优势,BDS观测值的3个组合中只有1个组合符合该结论。整体而言,这一现象并不明显。考虑是因为当前GNSS-IR测高精度较低,而该误差项改正的精度提升相对较少。本文的两种方法均可用来进行GNSS-IR海面测高。但从电离层残差项会影响GNSS-IR海面高度反演精度上来看,第2种组合方法更优。上述方法的引入增加了海面高度反演方法的多样性,为利用GNSS反射技术进行海面高度的反演提供了更大的适用空间。
本文利用单站24 h的模拟数据,对单频伪距与组合值中未被去除的电离层延迟误差对GNSS-IR测高反演的影响进行了分析,发现在SC02站某天的模拟数据中,得到反射面高度由于电离层延迟残差的存在有[-2,6] cm的偏差。但该值只是对该站该天的数据而言,只能作为定性分析的依据,并不能作为定量分析的结果,这是因为模拟数据是根据单站、单天的电离层数据插值而来,而电离层延迟误差的特性会因为站所处的位置和时间而变化。综合上述电离层影响的特点,定量研究电离层延迟对GNSS-IR海面高度反演也是一项重要且复杂的工作,需要在孤立GNSS-IR各项误差影响的基础上,针对电离层的不同特点对GNSS-IR海面高度反演精度的影响进行逐一分析。本文只是为了引入后一种组合方法,在模拟的基础上,简单对前一种方法中利用低通滤波器去除电离层延迟后仍存在残差并会最终影响GNSS-IR反演精度的问题进行了初步探讨。而后一种组合方法可以避免电离层延迟残差的存在。更值得一提的是,电离层会发生如闪烁等异常的情况。电离层异常会导致卫星信号失锁、伪距异常、载波相位观测值中周跳发生率提升[29]等,致使经由本文所述的伪距和单频载波相位组合实现的GNSS-IR海面高度反演精度更差,且也会影响伪距和双频载波相位组合值的反演精度。因此,电离层延迟对GNSS-IR海面高度反演的影响有待进一步的详细研究。
在两种组合方法中,通过对电离层延迟项的模拟,理论上第2种组合方式可削弱第1种组合中电离层延迟项对反演结果的影响,进而提升GNSS-IR测高反演精度,该提升范围在本文的模拟中小于2 cm(实际数据处理中该值可能因为站所处位置而有所不同)。由试验结果可知:由于当前GNSS-IR海面高度反演精度较低,如本文试验数据的反演精度均在分米级,且该反演精度受多种误差(包括随机噪声、动态海面、对流层延迟、电离层延迟、海面粗糙度、观测值采样率、平均反射面高度及高度角和方位角选取范围等)的联合影响,导致本文利用第2种组合方式处理实测数据在反演精度上并没有明显提升。但考虑到未来采用各种方法削弱各误差项的影响进而提升GNSS-IR的反演精度是该领域的重点研究内容,而本文所引入的第2种组合可以避免电离层延迟残差的影响。因此,本研究所引入的第2种组合方法是具有一定理论意义的,且本文所采用的模拟方法对之后研究电离层延迟对GNSS-IR测高反演精度的影响具有积极的启发意义。
为进一步提高利用本文所述方法反演海面高度的精度,未来工作会考虑建立波谱分析后峰值频率和反射面高度之间的函数模型[24-25]来削弱误差影响。

