空间网络对时序InSAR相位解缠的影响——以Delaunay与Dijkstra网络为例

马张烽，蒋 弥，李桂华，黄 腾

1. 河海大学地球科学与工程学院，江苏 南京 211100； 2. 中山大学测绘科学与技术学院，广东 珠海 519082

相位解缠是时序InSAR(interferometric synthetic aperture radar)技术至关重要的一个数据处理步骤[1-3]。能否准确估算出缠绕于[-π,π)的相位观测的2π模糊度个数是InSAR监测成败的关键。该步骤主要面临两个挑战：①判断出存在模糊度的观测点；②如何正确解算出对应的模糊度。相位连续性假设是解决上述挑战的基础，即相邻两个待解缠点的真实相位差(相位梯度)绝对值应小于π[4]。

基于此假设，最小二乘、最小费用流和最小不连续图等Lp范数方法[5]通过最小化缠绕相位梯度与真实相位梯度的范数距离来获得可靠的解缠结果。虽然上述方法在很多案例里都有出色的表现[6]，但低相干区域的强相位噪声、大气湍流和高相位梯度(变形或局部地形)都在不同程度地影响着局部相位差，导致相位连续性假设在实际的干涉图中并不能处处成立，导致解缠误差的产生并进而影响InSAR监测结果。

为减少相位不连续性带来的解缠误差，学者们采用了不同的处理策略。文献[7]提出的一维+二维方法将时域最小费用流网络规划与空间解缠相结合，以缓解较大相位梯度对结果造成的影响，从而逼近相位连续性假设。文献[8]提出了一种两步三维解缠算法，该算法通过在时间维进行低通滤波缓解高相位梯度，并根据噪声程度估计准确的权重，然后在空间维使用网络将所有离散点进行连接并进行相位模糊度的计算，获得了较好的解缠精度。文献[9]提出了基于三角无旋性假设的三维解缠算法，该算法利用时间和空间维度上的三角相位闭合差来优化无旋性约束，逼近相位连续性假设，从而获得了较稳健的解缠结果。

虽然时间序列InSAR相位解缠历经近20年发展，但是解缠算法的理论框架却大相径庭。即便如此，大多数方法在构建空间网络时均使用了Delaunay三角网[10]，并在此网络的基础上根据网络边所包含的两点之间的相位差解算所有点的模糊度。尽管目前Delaunay三角网应用广泛，且在许多软件中(如GAMMA软件)，均被作为默认的解缠网络[11]，但也不乏一些负面的案例。例如在桥梁等三维结构较复杂的建筑物的解缠过程中，Delaunay三角网并未获得可靠的解缠结果[12-13]。考虑到Delaunay三角网的表现以及在解缠中的定量表现仍不明确，本文从理论和实测角度评估了Delaunay三角网对时序相位解缠的影响。结果表明，由于Delaunay三角剖分算法在构网时仅考虑了拓扑关系，并没有将相位连续性假设作为约束，因此容易触发高相位梯度的边，导致解缠错误。为解决这一问题，本文首先使用时间相干性度量干涉图中指定边的相位梯度，再引入图论中的Dijkstra最短路径算法[14]，引导选择低相位梯度的边，从而逼近相位连续性假设。为公平比较网络性能，本文在对比过程中均采用了相同的最小费用流方法[15]对网络进行解缠。模拟和真实数据的对比研究表明，本文构网方法较现有Delaunay网络能够更为高效地执行相位解缠，提高时序解缠精度。

1 面向Delaunay三角网的解缠方法

Delaunay三角网自Dirichlet 1850年首次提出在空间约束下根据离散点集合生成三角网的思想后[10]，经过170年的发展已经产生了诸多变种，本文仅对经典Delaunay生成算法进行简要回顾。

在二维平面中给定K个离散点集合Pi,i=1,2,…,K，对每一个离散点Pi都生成一个相对应的凸包γi，γi的特征表现为：γi上所有包含的点离Pj的距离总是要远于与Pi之间的距离(凸包所包含的点并非待生成三角网的离散点)。这些凸包构成的图形被称为Voronoi图。Voronoi图中一个公共点包含3个凸包γm、γj与γk，且3个凸包相邻且互相存在公共边，将3个凸包所代表的离散点Pm、Pj与Pk相连，则构成了基本的Delaunay三角形。重复三角形的生成则构成了最后的Delaunay三角网。

Delaunay三角网具有以下两个特征：①构网唯一，即所有离散点集合只能生成唯一的三角网；②三角网内所有三角形互不重叠。

在最小费用流解缠(MCF)方法中，生成的三角网中每个三角闭合环Trii都代表着最小的独立闭合图形。在每个三角图形单元中，3条边的缠绕相位差之间存在着无旋性约束条件Ui[16]

Ui=round(-δφm,j/2π)+round(-δφj,k/2π)+

round(-δφk,m/2π)

(1)

式中，δφm,j、δφj,k及δφk,m分别为三角形中邻近3个点m、j和k的缠绕相位梯度；round为取整算子。

假设生成的三角网中含有M个三角形，且由N个边组成，则所有边E的待求模糊度与所有无旋性约束所对应的设计矩阵AM×N表示如下[16-17]

(2)

联合设计矩阵与无旋性约束可以求取所有边的模糊度X，模糊度、设计矩阵与无旋性约束之间存在的线性关系及求解模糊度的目标函数表示如下

(3)

式中，f代表相位梯度概率密度函数计算出的极大似然费用[18]。

由于待求解模糊度的整数特征，且三角形个数M通常小于边个数N，A存在秩亏现象，因此常规最小二乘无法求解。考虑到部分边不存在模糊度，即待求解K表示为稀疏特征，因此式(3)的解算需要由对于稀疏待求解有较好表现的整数线性规划完成。由于采用的整数线性规划求解式(3)时存在加权过程，这里的权值通常在网络规划中被认为是通过路径产生的费用，因此加权的整数线性规划也通常被称为最小费用流方法[19]，本文最小费用流的求解过程均采用GUROBI软件中的“intlinprog”整数线性规划子函数完成。

需要注意的是，在上述目标函数完成优化后，仅计算出了每条边的模糊度。因此还需要通过漫水填充(flood-fill)的方式，将边的模糊度积分至每个点，最后将每个点的模糊度添加到初始缠绕相位上完成解缠。

2 面向Dijkstra网络的时序解缠方法

2.1 Dijkstra最短路径算法

最短路径问题是经典图论研究中的一个基本问题，主要目标是最小化指定起点i与终点j间的连通路径的长度或权重。Dijkstra方法是最短路径搜索算法中最具代表性、计算效率最高的经典算法之一，其核心思想在于[20]：给定一个无向双连通图G=(V,E)，其中V和E分别代表节点与边；Dijkstra算法在初始搜索过程中，对起点i与终点j之间的路径赋予0值，接着添加E中的一条连接边至备选路径并更新路径长度，在路径的搜索中始终保持着松弛操作，即在搜索过程中可能驳回上次搜索的结果并重新开始搜索其他可能的连接边，直至松弛操作结束后，获得起始节点i到终点j由多条边组成的最短路径。

鉴于Dijkstra算法能够对任意两点的路径进行筛选，根据权值或边长规划最优路径(边)集合，因而可用于提炼Delaunay三角网中任意两个相干目标的连接，即采用权值更小的边集合来代替权值更大的边。在之前的研究中，虽然文献[21]已考虑用更新的网络进行形变参数(高程误差和速率)估算，但是网络形态根据具体规则进行改变能够提升解缠精度仍缺乏深入的研究。

2.2 Dijkstra网络解缠

前已述及，Delaunay三角剖分准则是相邻3个凸包是否存在公共点以及两两之间是否存在公共边，而未考虑生成的三角形中顶点与顶点间的相位连续性。由于变形信号、大气湍流和相位噪声的存在，Delaunay网络中部分边并不能满足先验假设。这会引起相位差大于π的概率增大，导致模糊度的错误估计。为了得到更好的解缠结果，需要消除或替换存在违背相位连续假设的边。因此，这个优化过程可以简化为一个网络优化问题。本文提出利用Dijkstra算法去完成网络的优化，将点与点之间的相位变化的程度作为边长，变化程度越大的边的边长越长，变化程度越小的边的边长越短。在路径优化中，相位变化程度越小的边越容易被接受，变化越大的边越容易被舍去，因此更容易满足相位连续性假设。

对于时间序列数据，度量空间上两个相干目标i和j的相位变化程度的有效方法之一是时间相干性γi,j[21]

(4)

式中，δφi,j,p表示M幅干涉图中第p幅干涉图i，j像素间的相位差,在网络搜索过程中，路径的长度为-10lg10(γ)。

由式(4)可见，时间相干性由干涉图序列同一位置的边的缠绕相位梯度求复数模叠加而来，相位梯度越小，时间相干性越接近1，相位梯度越大，时间相干性越接近0。因为时间相干性实际上反映了时序干涉图相位梯度的平均水平，所以以时间相干性作为优化准则的网络重构方法有利于提高整个时序相位解缠的精度。

将Dijkstra算法与时间相干性结合实现网络优化的过程可以归纳为两个基本步骤：①给定初始的无向双连通图G=(V,E)；②利用Dijkstra搜索给定起点集合S与终点集合D之间的最短路径并记录,直到遍历所有待搜索路径。在步骤②的搜索过程中本文将Delaunay三角网上的每条边的端点作为Dijkstra搜索的起点与终点。由于计算所有边的时间相干性十分耗时，本文采用KNN(K-nearest neighbor)算法搜索距离每个点邻近的50个离散点来完成E的构建，并将E与Delaunay三角网的边集合合并生成的新的集合E。使用这种策略的依据是随着两点欧氏距离的减小，相位梯度可能更小。在步骤②中，根据相干性的高低，任何S与D直接相连的边都有可能被集合E中的边代替。

在完成Dijkstra网络的搜索后，Delaunay三角网中时间相干性低的初始边集合都被更新，替换成了搜索出的最短路径的边集合，由此生成了全新的网络。值得注意的是，该算法并不能确保三角形完整，那些被取代了边的三角形可能遭到破坏，也摧毁了MCF解缠三角无旋性约束，因此这些边需要针对性地进行三角形重构。在重构之前，需要根据简单的拓扑关系判断出哪些边仍不存在任何三角形中，这个拓扑关系可以描述为：如果一条边所在的两个端点，没有另外两条存在公共端点的边与之相连，则判断此边不存在于任何三角形中。提取出这些边后，根据每条边的顶点生成待选边集合，待选边由两个顶点的KNN生成的邻近边组成，选择待选边中存在公共端点且边长之和最短的两条边作为新三角的两条边。根据此思路可以生成的新的三角网络并产生新的三角无旋约束。

新生成的Dijkstra网络与Delaunay三角网解缠的过程一致，均使用基于三角无旋约束的最小费用流方法进行解缠，两者唯一的差异则为网络形态的不一致。因此，对比两者网络解缠结果的优劣可以判断哪种网络更适用于相位解缠。

3 试验与分析

本文使用模拟数据和真实数据分别对基于Delaunay三角网与Dijkstra网络的相位解缠进行了评估。

3.1 模拟数据

本文模拟了一个边长为200 km的正方形区域，在正方形区域中随机选择了10 000个离散点，如图1(a)所示，并模拟了50幅干涉图，每幅时间间隔步长为12 d，模拟的线性变形速率(mm/a)由Matlab中Peaks函数提供。第50幅干涉图的形变相位如图1(a)所示。在此基础上，根据分形模型模拟了大气噪声(大气绝对值相位不超过π)与相位随机噪声。此外，所有干涉图的随机噪声的大小设置为与相干性0.3条件下的相位噪声相等[22]。第50幅干涉图大气分量和噪声分量的模拟相位分别如图1(b)和图1(c)所示。图1(d)为模拟的包含变形、大气和噪声元素的第50幅干涉图。

(1) 评估Dijkstra算法对Delaunay网络进行更新的能力。与图1(e)中所展示的Delaunay网络的时间相干性相比，图1(i)中Dijkstra时间相干性有所提高。该结果验证了Dijkstra在寻找更可靠边的能力。此外，不同网络的解缠结果的准确性也是评价不同网络的重要指标。图1(g)和图1(k)分别展示了第50幅干涉图的解缠误差。对照图1(f)和图1(j)的解缠结果可以看出，用Delaunay网络进行解缠的结果误差大于Dijkstra网络的解缠结果，而误差主要集中在相位梯度大的位置，这说明通过引入时间相干性来考虑相位差的Dijkstra网络更容易满足相位连续性假设。在图1(l)和1(h)中试验还比较了整个时序干涉图(50景)中模糊度估计误差的绝对值之和，一个模糊整数对应2π解缠误差。结果表明，基于Dijkstra网络的模糊度估计误差小于基于Delaunay网络估算的模糊度误差，尤其是在高相位梯度的区域。

图1 模拟干涉图及Delaunay网络与Dijkstra网络解缠性能比较Fig.1 Simulated interferograms and the phase unwrapping performance comparison between Delaunay network and Dijkstra network

(2) 进行蒙特卡罗模拟试验，测试Dijkstra相比Delaunay具体可以减少的解缠误差百分比。在模拟试验中，相干性被设置为不同的值，范围在0.05～0.95之间。在每次仿真中都记录了包含解缠误差的点的百分比。给定的不同的相干性数值下，模拟试验重复1000次。1000次模拟试验的平均结果如图2所示。由图2可以看出，在大多数相干情况下，Dijkstra网络的解缠误差均比Delaunay网络小约3%～8%，这验证了网络质量对相位解缠的重要性。当相干性接近1时，表明Delaunay网络上的边都具有很高的相干性，因此Dijkstra算法更新前后网络几乎无差异，即当前的边集合就是最优的路径。

图2 各相干性条件下，两种网络的解缠误差比例Fig.2 Percentages of points with unwrapping errors

3.2 真实数据

本文选取COMET LICS[23]平台处理的Sentinel-1A Track128上93幅未经滤波的小基线集干涉图(子集最长时间基线36 d，如图3中时空基线图所示)作为真实数据，影像观测时间覆盖2019-01-09—2020-02-09，影像观测时间间隔为12 d。Track128影像覆盖区域见图3，图3(b)为切割后试验区的Sentinel-2光学影像，该地区覆盖着大面积植被，相干性较低且地形较为复杂，适合作为判断解缠方法性能的区域。在选取93幅干涉图后，利用LICS平台提供的所有干涉图的相干性计算出平均相干性，选取平均相干性大于0.25的点作为相干目标点，进行构网和解缠。

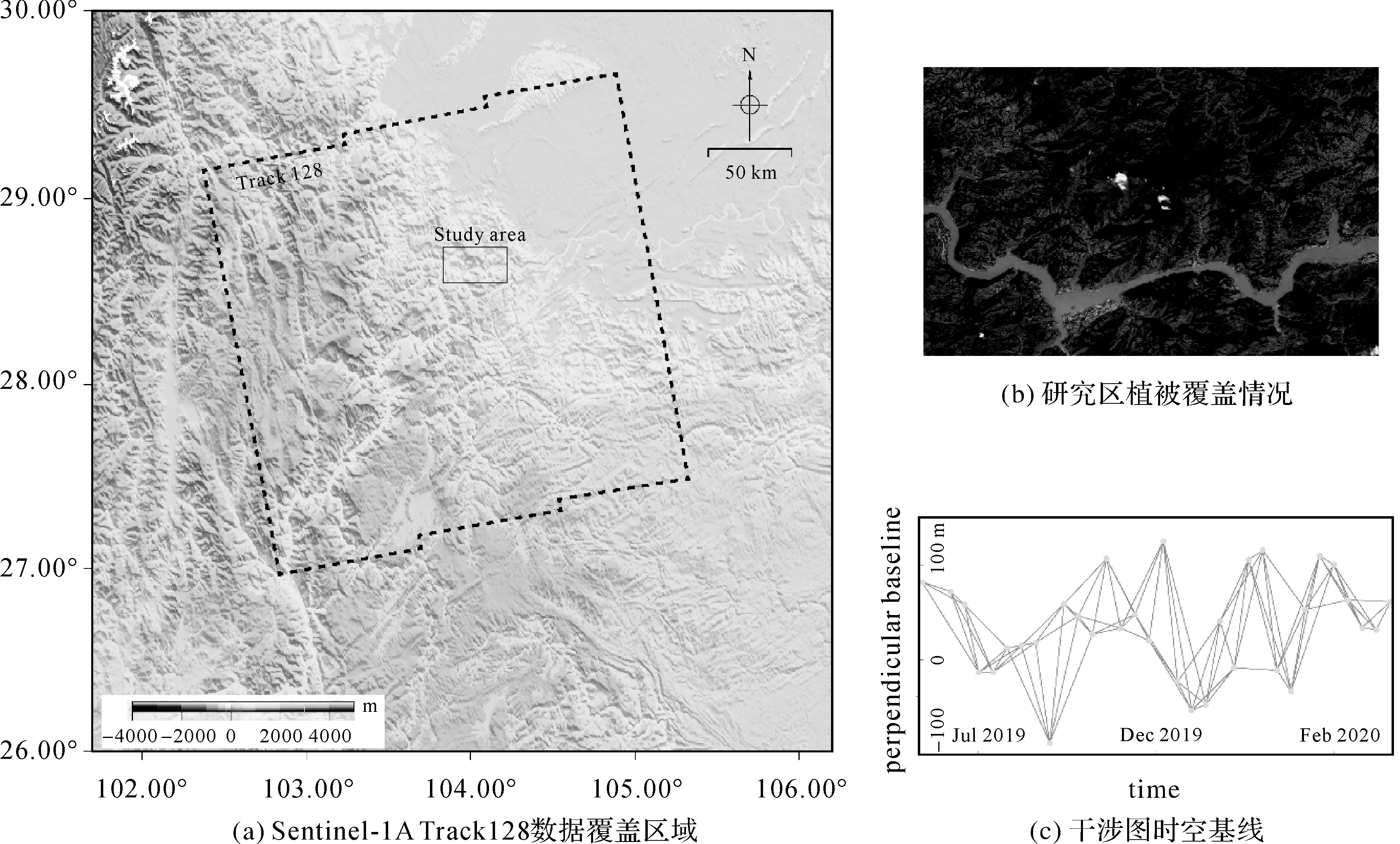
图3 研究区域概况及干涉图Fig.3 Overview of the study region and the general information of the used interferograms

图4展示了Delaunay三角网与优化后的Dijkstra网络基于93幅干涉图计算出的时间相干性。可以看出Delaunay三角网中时间相干性较低的区域在经过Dijkstra优化后总体上得到了提升，由图4(a)与图4(b)中局部区域的缩放图可以看出，时间相干性较低的边被周围相干性较高的边所取代，时间相干性较高的边则被进一步保留，因此可以进一步说明Dijkstra网络在生成过程中，对时间相干性较低的边进行了更新，时间相干性较低的边会被两条或两条以上的边所替代，而原本时间相干性较高的边则不会被替换从而被保留了下来。因此，最后生成的Dijkstra网络较Delaunay网络整体时间相干性有所上升，这也直接反映出在Delaunay三角网中相位差较大的边已经被减少，并被相位差较小的边所替代。

图5给出了2019-08-01—2019-09-06与2019-10-12—2019-11-05两期干涉图解缠的结果。从目视解译可知，Delaunay解缠结果(图5(c)—(d))中存在较多相位不连续的区域，这些区域表现为与邻近区域相差2π，说明这些不连续的区域存在解缠误差，且这些区域大多为图4中时间相干性较低的区域。而Dijkstra解缠后相位(图5(e)—(f))在空间上比较连续，相位不连续的区域被减少。值得注意的是，在Delaunay解缠结果中存在相位不连续的区域，在Dijkstra的解缠结果中存在较少与邻近区域有2π跳变的情况，所以可以判断Dijkstra网络时间相干性的优化对相位解缠起到了积极的作用。

图5 缠绕相位图与两种网络解缠相位图Fig.5 Wrapped and unwrapped interferograms

定量方面，本文沿用当前解缠误差检验的方法，通过统计时间维的三角闭合差作为解缠误差的评价标准[24-25]。相位三角闭合差Δψ表示时空基线平面(图3(c))形成三角闭合环的3个干涉图解缠后的相位差，闭合差对应的模糊度估计错误个数μ[25-26]

(5)

为方便表述，这里将处于相位三角中的干涉图分别用数字1、2、3表示。另外，本文还使用解缠后干涉序列反算出的时间序列相位与解缠序列的残差来衡量解缠精度，其值越小，说明解缠越可靠。

图6展示了在两种量化标准下各方法的评估结果。相比图6(a)中Delaunay三角网的模糊度误差个数，图6(b)中Dijkstra网络的模糊度误差个数减少，且减少区域对应时间相干性提升的区域，因此可以判断考虑相位梯度，并以此改善网络形态的Dijkstra网络的确能够更好地满足相位连续性假设，从而减少解缠误差。对比模糊度误差个数直方图，Delaunay峰值为45而Dijkstra为30。相比而言，Dijkstra网络减少了约33%的模糊度解算错误造成的不闭合三角环数。此外，对比两者解缠结果的时间相干性及其统计直方图可以发现，Dijkstra网络相比Delaunay三角网整体时间相干性更高，整体相干性提升约0.05，这也代表提升时间相干性的Dijkstra网络更有益于InSAR时间序列的解算。

图6 两种网络解缠结果中存在的模糊度错误个数以及对应解缠结果估计出的时间相干性Fig.6 The sum of absolute value of ambiguity error and temporal coherence respectively for Delaunay network and Dijkstra network

图7统计了两种网络在解缠过程中的费用和解缠效率。对于93幅干涉图的解缠，Delaunay三角网消耗的费用(图7(a))均高于Dijkstra网络，相应的解缠消耗时间(图7(b))也高于Dijkstra。这两者的增益均来自Dijkstra网络中高相位梯度的边被减少，因此需要解算的存在模糊度的边也被减少，相对应解缠消耗时间则减少。从这些试验中可以得出如下结论：就相位解缠而言，Delaunay三角网从精度与效率方面均非最优选网络，Dijkstra网络在这两个方面均优于Delaunay三角网。

图7 Delaunay三角网与Dijkstra网络的解缠费用与消耗的时间对比Fig.7 The total cost and computational time for unwrapping based on Delaunay network and Dijkstra network

由于选取区域缺乏实测数据进行InSAR结果的验证，且解缠整体的提升效果难以通过点的对比进行体现，因此，本文进行了进一步试验以说明解缠对形变解算所产生的影响，本文计算了从小基线集相位到单主影像转换过程中的均方根误差，对两种网络解缠相位的均方根误差进行了对比。因为两者相位只有解缠网络的不同，因此均方根误差的大小变化可以认定为是由解缠误差所带来的。均方根结果如图8所示为表征解缠结果对形变解算的影响。

图8(a)、(b)分别为Delaunay与Dijkstra网络解缠结果的均方根误差，图8(c)为两者结果的直方图对比，根据两者的对比可以看出，Dijkstra网络小基线集相位到单主影像转换的模型均方根误差明显更小，因此可以确定Dijkstra网络对于相位解缠精度的提升有益于形变量的解算。

图8 小基线集与单主影像相位转换过程中的均方根误差Fig.8 RMSE of single-reference phase converted from SBAS phase

4 结 论

本文针对InSAR时间序列相位解缠中常用的Delaunay三角网性能进行了评估，并提出了Dijkstra网络与之进行了解缠性能的对比。Dijkstra网络利用相位梯度计算时间相干性，并将时间相干性作为衡量路径长度的指标，在此基础上，利用Dijkstra算法对Delaunay三角网进行优化，以低相位梯度的边取代了高相位梯度的边，最大化了网络的时间相干性，从而逼近了相位连续性假设。模拟和真实试验均表明Delaunay三角网并不是相位解缠的最优选择，Dijkstra网络在精度与效率方面具有更好的表现。尤其在精度方面，Dijkstra网络的解缠模糊度误差个数较Delaunay三角网减少接近约33%。此外本文研究结果证明空间参考网络的质量优化也是提升解缠性能的关键步骤之一。

致谢：感谢ESA/Copernicus提供的Sentinel-1数据。