GLONASS频间码偏差实时估计方法及其在RTK定位中的应用

徐龙威，吴忠望，董绪荣

航天工程大学航天信息学院，北京 101416

观测值频间偏差(inter-frequency bias,IFB)一直是影响GLONASS导航定位性能的重要因素。IFB主要是源于同一频段(L1/L2)上不同GLONASS卫星的观测信号硬件延迟差异[1]。在基于双差模型的基线解算中，观测值站间单差能够消除卫星端IFB，而接收机端IFB受测站固件设备影响，难以直接消除。按观测值类型，IFB可划分为频间相位偏差(inter-frequency phase bias,IFPB)和频间码偏差(inter-frequency code bias,IFCB)[2]。文献[3—4]指出IFPB的本质是伪距观测值和载波观测值的硬件延迟之差，并将IFPB划分为数字信号处理引起的延迟和硬件本身引起的延迟两部分，且数字信号处理引起的延迟占主要部分，因此，IFPB与信号频率和接收机类型有很强的相关性。基于IFPB与信号频率的线性关系，许多学者采用估计IFPB变化率、构建纯载波观测值组合等方式，实现了毫米级的IFPB改正，消除IFPB对高精度定位的影响[5-9]。IFPB相关参数已经引入接收机独立交换格式RINEX3.03文件和差分GNSS数据传输协议RTCM10403.X中，在导航定位服务中取得了良好的应用[10]。

IFCB主要因接收设备的前端带宽和相关器设计导致的芯片畸变产生，且每个信号通道的畸变量存在差异[11]。与能够高精度模型化的IFPB相比，IFCB的变化规律较为复杂[12]。文献[13]采用精密单点定位模型估计了来自5家厂商的133台接收机的非差消电离层组合IFCB，验证了接收机或天线的品牌、系列和固件版本都会对IFCB的量级产生影响。文献[14—15]提出了组合观测值的IFCB的估计策略，指出虽然IFCB与频率存在相关性，但难以构建通用的高精度线性模型，且个别测站的IFCB存在明显差异。综合多位学者的研究成果，IFCB的主要特性可归纳为：①L1和L2上IFCB的量级不同，都具有一定的长期稳定性；②同质基线的IFCB量级相差很小，但也有一些特例存在；③异质基线的双差IFCB可达数米；④不同接收设备的IFCB与通道号的线性关系不一致，导致IFCB无法采用统一模型改正。本文将GNSS信号接收设备(接收机类型、固件版本、天线类型)完全相同的测站构成的基线称为同质基线，其他基线统称为异质基线。

由于IFCB难以基于经验模型改正，在异质基线或精密单点定位解算中，通常将每颗卫星的IFCB或其与频率号相关的变化率作为一个静态参数估计。文献[13—15]将基于历史观测值估计HMW或消电离层组合的IFCB用于GLONASS伪距组合观测值实时改正。文献[16]直接将各颗卫星IFCB作为一个静态参数估计，进行载波观测值变换合成超窄巷模糊度，实现长基线GLONASS模糊度固定，但该算法受限于观测值噪声，仅能用于事后解算。文献[17]在RTK定位模型中，将IFCB与频率号相关的变化率作为静态参数进行估计，但从其结果来看，IFCB变化率参数估计策略显然是不符合IFCB特性的。文献[18]提出了一种用于精密单点定位消电离层组合的IFCB实时改正方法，能够明显改善GLONASS PPP定位的收敛速度和浮点解精度。德国地学研究中心(German Research Centre for Geosciences,GFZ)已经开始发布与接收机类型相关的消电离层组合IFCB[19]。但是，上述研究都是针对观测值组合的IFCB，且难以直接用于GLONASS实时非组合模糊度固定。尤其是异质基线的中长距离RTK定位解算，伪距观测值的IFCB可导致模糊度参数估计偏差，进而模糊度固定困难。

本文针对异质基线GLONASS双差IFCB难以消除的问题，基于HMW组合和消电离层组合观测值，提出一种非组合站间IFCB估计方法，对两个频段伪距观测值的站间IFCB进行研究，并将该算法用于GPS/GLONASS组合RTK定位解算。需要指出的是，本文主要对GLONASS IFCB特性进行研究，IFPB直接采用相关学者发布的先验值进行改正[5]，见表1。

表1 各厂家的GLONASS IFPB变化率先验值Tab.1 The priori corrections of GLONASS IFPB rate for receivers of different manufacturers

1 数学模型

1.1 GLONASS站间IFCB估计方法

GLONASS双差观测值可模型化为[5]

(1)

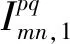
双差HMW(Hatch-Melbourne-Wübbena)组合可分解为一个双差伪距窄巷组合(narrow-lane,NL)和一个双差宽巷载波组合(wide-lane,WL)，顾及GLONASS IFB的影响，HMW组合可模型化为[15,20]

(2)

(3)

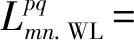
(4)

式中

(5)

(6)

(7)

综合式(2)—式(7)可获双差IFCB的窄巷组合，如式(8)所示

ξL,HMW

(8)

式中，单差宽巷模糊度可以通过伪距观测值和载波观测值做差直接获得。文献[21]中给出了GLONASS宽巷模糊度实时固定方法，IFPB采用先验值修正，于是式(8)等号右侧部分可以实时获取。

GLONASS双差伪距观测值消电离层组合可表示为

(9)

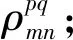
将对流层湿延迟模型化为天顶对流层湿延迟和VMF1映射函数，可得式(10)

(10)

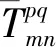
基于式(8)和式(10)，可得一个GLONASS卫星非组合双差IFCB解算方程

(11)

通过矩阵转换，可将双差IFCB参数变换为站间单差IFCB，如式(12)所示

(12)

为消除方程秩亏，将参考卫星各频段(P1、P2)站间IFCB为0，测站间天顶方向对流层湿延迟等于0，3个条件作为虚拟观测值引入模型，可得非组合站间IFCB的估计模型

(13)

1.2 站间IFCB实时改正的RTK定位解算流程

常规GNSS的RTK函数模型[9]为

(14)

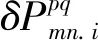
综合式(1)和式(14)可知，若RTK函数模型未顾及GLONASS站间IFCB，站间IFCB与电离层参数具有相关性，式(14)中电离层和模糊度参数的含义为

(15)

(16)

对于忽略大气延迟参数的短基线RTK，站间IFCB也会影响流动站坐标改正参数的估值，导致模糊度参数收敛速度减缓。

基于上文的GLONASS站间IFCB估计方法，本文提出一种实时修正GLONASS站间IFCB的RTK定位解算模型，如式(17)所示。利用文献[21]的中长距离基线解算模型，进行GPS/GLONASS组合RTK定位，获得GLONASS宽巷整周模糊度和流动站近似坐标，实时估计GLONASS站间IFCB。并将宽巷模糊度作为RTK定位解算的未知参数，构建RTK定位模型，实现站间IFCB改正和RTK定位同步进行

(17)

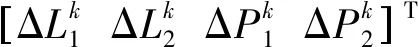
图1给出了站间IFCB实时改正的RTK定位解算流程，可划分为以下4个步骤：

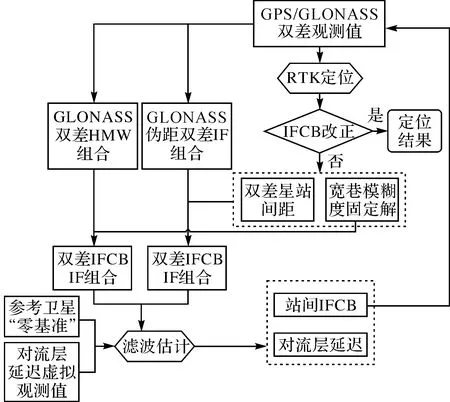
图1 站间IFCB实时改正的RTK定位解算Fig.1 Real time inter-station IFCB correction algorithm in RTK

(1) 采用式(17)进行RTK定位解算，如果已经改正IFCB，直接输出定位结果，结束当前历元解算。

(2) 若未改正IFCB，则输出双差星站间距和宽巷模糊度固定解，分别与GLONASS伪距双差消电离层组合和HMW组合一起，基于式(8)和式(10)，获得双差IFCB窄巷组合和消电离层组合观测量。

(3) 基于双差站间IFCB宽巷组合和消电离层组合，引入参考星“零基准”和站间天顶对流层延迟虚拟观测值，构建式(13)模型，滤波估计站间IFCB，实时改正GLONASS双差伪距观测值。

(4) 站间IFCB改正后，重新开始步骤(1)的解算，输出RTK定位结果。

本文在基线长度小于20 km的RTK定位中忽略大气延迟的影响，中长距离的RTK定位将大气延迟作为参数进行估计。对流层延迟先利用经验模型改正干分量、湿分量作为未知参数估计。将各颗卫星L1的双差电离层延迟作为未知参数估计且历元间不相关。

2 试验与分析

2.1 试验说明

试验数据源为欧洲区域参考框架连续GNSS观测网络(EUREF permanent GNSS network,EPN)24个基准站的观测数据(http:∥www.epncb.oma.be/index.php)[24]，构建12条基线进行RTK定位解算，见表2。12条基线中BS10为同质基线，其他基线为异质基线。基线长度分布在0～130 km，BS01—BS03基线长度小于5 km；BS04—BS12基线长度在20 km以上。

表2 基线的测站接收机和天线信息Tab.2 Receiver and antenna on the two ends of baselines

本文进行了站间IFCB估计及特性分析、实时改正站间IFCB的RTK定位两个试验，其具体试验设置如下：

(1) 站间IFCB估计及特性分析试验。基于2020年DOY 100—DOY 119，20 d，采样间隔30 s，GPS/GLONASS观测数据估计站间IFCB并对其特性进行分析。采用参数可变的序贯最小二乘平差算法估计站间IFCB和测站间天顶对流层湿延迟参数。站间IFCB作为不随时间变化的恒定参数，天顶对流层湿延迟的过程噪声采用随机游走模型表示。顾及GLONASS伪距IFCB的影响，试验设定GLOANSS伪距的先验噪声为0.5 m，GPS伪距先验噪声为0.3 m，GPS和GLONASS载波相位的先验噪声为0.003 m；观测值高度角定权策略为P=1,el>30°;P=sin(el),el≤30°[14,25]。卫星高度角阈值为7°。由于各颗卫星的站间IFCB估值是基于一定基准的相对值，如果以双差解算的参考星为基准，解算过程中参考星的变换会导致站间IFCB的数值变化。为便于统计分析，站间IFCB单天解估计选取所有可见卫星各频段的站间IFCB之和等于0为基准，以确保整个解算过程的基准统一。

(2) 实时改正站间IFCB的RTK定位试验。利用2020年DOY 119的24 h，采样间隔1 s，GPS/GLONASS观测数据验证本文GLONASS站间IFCB实时改正算法对RTK定位解算的影响。观测值噪声、高度角定权和阈值、对流层延迟估计、站间IFCB估计等策略与试验(1)相同。以参考星的站间IFCB为0作为基准。RTK模糊度解算采用分步固定的部分模糊度固定策略。首先，采用取整算法固定宽巷模糊度，取整阈值为0.25周，浮点解理论成功率大于99.9%。其次，基于宽巷模糊度固定解更新解算方程，采用LAMBDA算法搜索窄巷模糊度，并进行ratio检验[26]，ratio阈值设为2.5。如果模糊度搜索未通过ratio检验，则删除搜索区域中高度角最低卫星的模糊度，重新搜索，直到通过ratio检验。RTK定位过程中，当前历元仅继承上一历元的浮点解，滤波解算后，重新进行模糊度搜索固定，以避免继承上一个历元错误的固定解。

为验证实时站间IFCB算法可行性，本文采用单GPS、未改正站间IFCB的GPS/GLONASS组合，以及实时改正站间IFCB的GPS/GLONASS组合3种RTK定位模式，分别以G、GRuc-IFCB和GR rtc-IFCB表示。RTK定位解算每小时初始化一次，统计其收敛时间、首次固定时间、模糊度固定率和定位偏差等指标。

2.2 站间IFCB估计结果和特性分析

图2给出了GLONASSR01卫星两个频段伪距(P1和P2)的站间IFCB单天解时间序列。各条基线站间IFCB存在明显差异，一些基线的站间IFCB接近3 ns，如基线BS06、BS09、BS12的P2站间IFCB。同一条基线P1和P2站间IFCB的量级存在很大差异，如基线BS04 P1站间IFCB约-0.4 ns，而P2站间IFCB达到2.6 ns。同质基线BS10的站间IFCB估值明显比异质基线小，其P1和P2上站间IFCB估值均小于0.3 ns。站间IFCB单天解估值具有一定的稳定性，如图3所示，所有基线的GLONASSR01卫星单天解的标准差均小于0.3 ns。受多路径等未模型化误差的影响，基线BS02 P1和基线BS05 P2的站间IFCB标准差较大，分别约0.24 ns和0.28 ns。

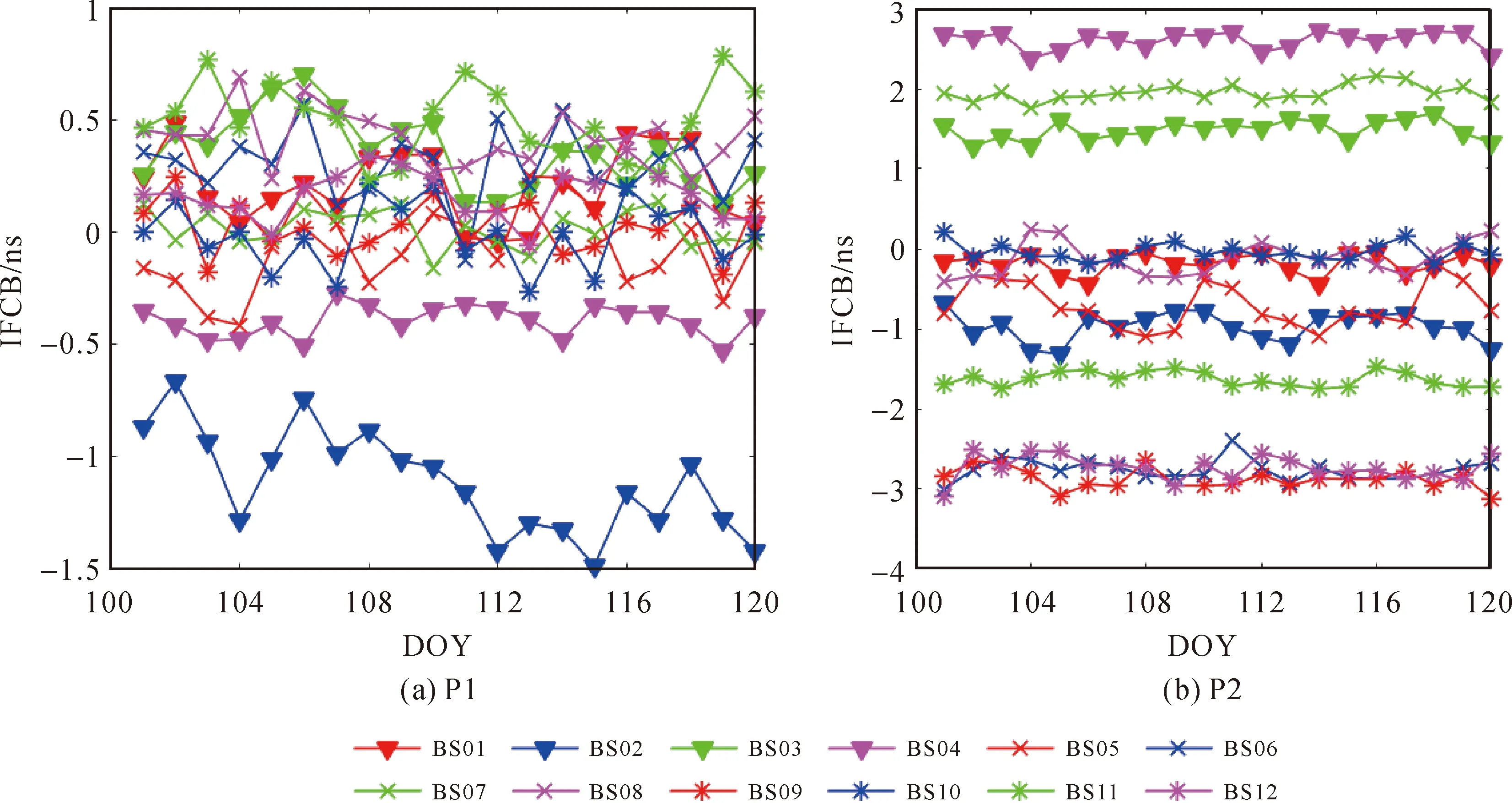
图2 GLONASS R01卫星站间IFCB单天解估值的时间序列Fig.2 Daily estimate values of GLONASS R01 inter-station IFCB

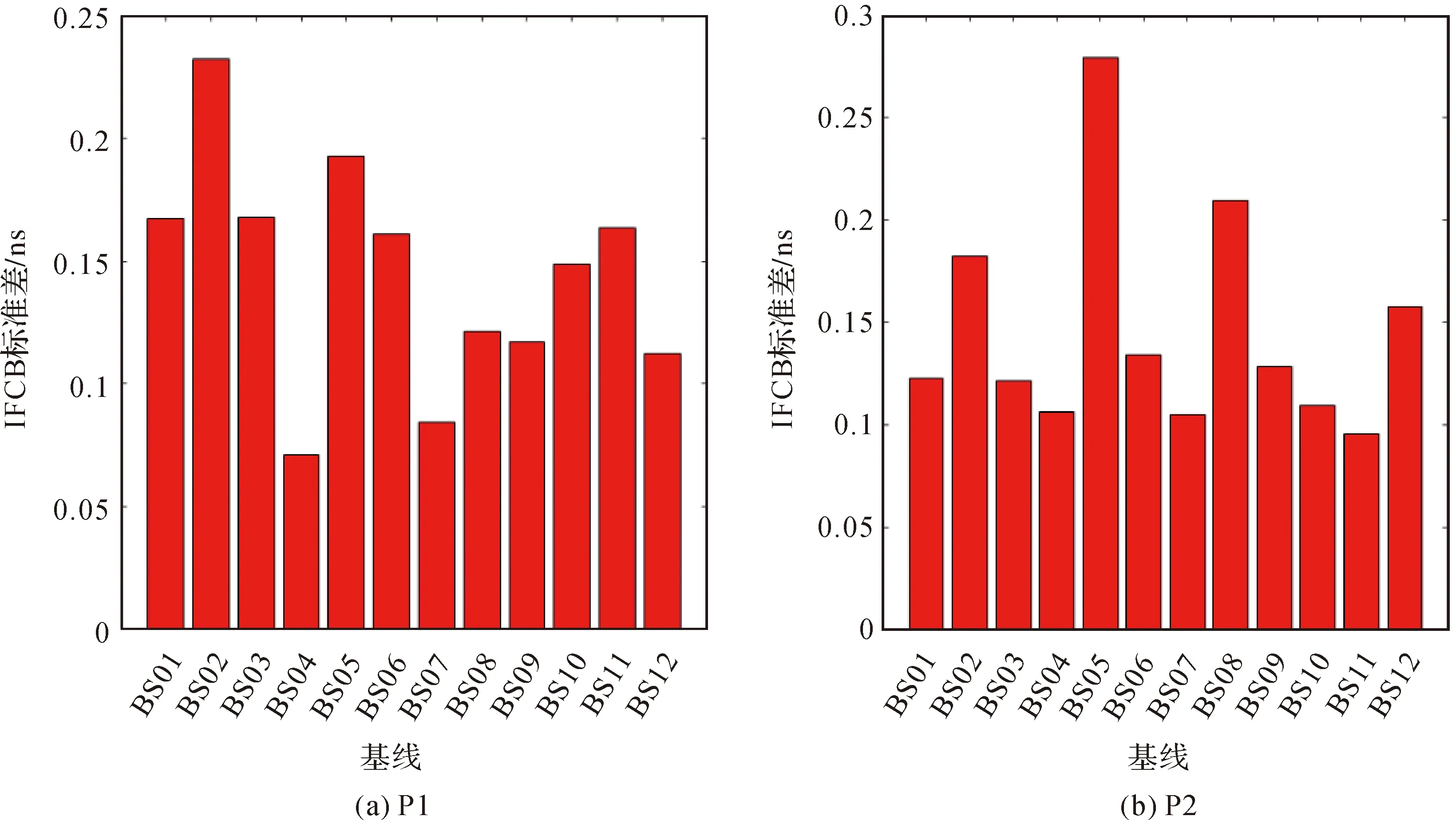
图3 GLONASS R01卫星站间IFCB单天解估值的标准差Fig.3 Standard deviation of daily GLONASS R01 inter-station IFCB

图4中给出了所有基线各颗GLONASS卫星的站间IFCB单天解估值均值。图4中信息能够证明基于图2和图3获取的结论具有普适性。以卫星R14为例，基线BS09 P1站间IFCB的量级接近6 ns；基线BS09和BS05的P1站间IFCB之差约10 ns。基线BS01 R12卫星P1站间IFCB小于-0.3 ns，而其P2站间IFCB接近-4 ns。同质基线所有卫星的站间IFCB估值分布在[-0.6,0.6] ns区间内。

图4 各颗GLONASS卫星站间IFCB单天解平均值Fig.4 The averages of GLONASS inter-station IFCB daily estimate values

图5给出了R09卫星改正站间IFCB前后的伪距观测值残差。由图5可知，BS01 P1、BS05 P1、BS09 P1、BS09 P2都存在明显的系统性偏差。例如，BS09 P2的残差分布在区间[0，5] m之间，均值在2.3 m左右。由于参考卫星的变换，BS05 P1残差在两个观测时段的系统偏差项不同。改正站间IFCB以后，所有卫星的伪距残差分布区间明显向0平移，BS05伪距残差在两个观测时段的分布区间差异也被消除。

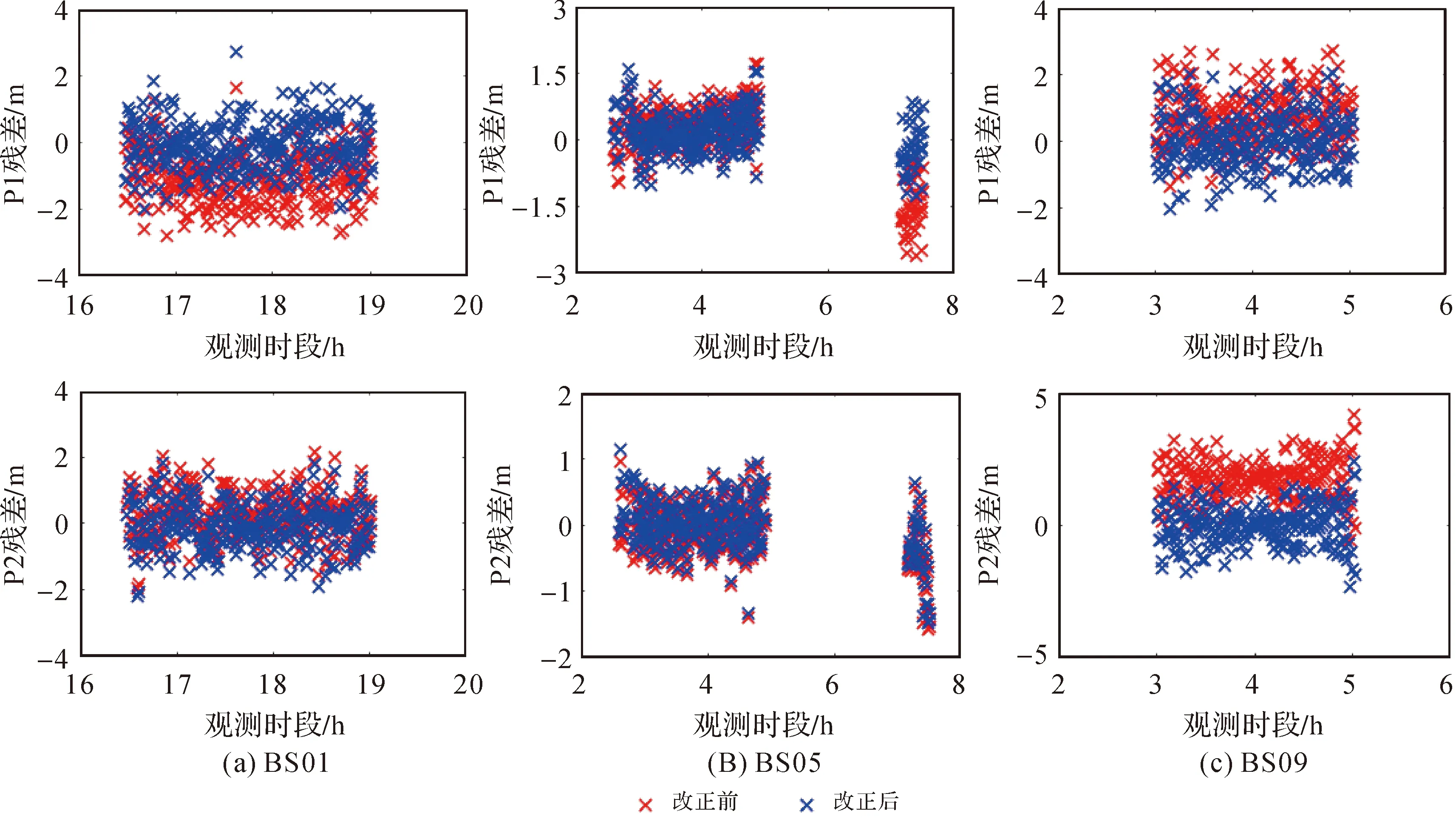
图5 卫星R09改正站间IFCB前后的伪距观测值残差Fig.5 Residual errors of R09 pseudorange observations before and after IFCB correction

2.3 站间IFCB改正对RTK定位的影响

站间IFCB导致异质基线双差伪距观测值的系统性偏差，影响RTK定位结果。由于IFCB与接收机类型、固件版本和天线类型相关的复杂特性，甚至同质基线也可能存在系统性偏差。因此，需要采用与接收设备无关的实时校正算法，实现伪距观测值系统性偏差的消除。

图6给出了短基线BS01、中距离基线BS05和长距离基线BS09的R01、R07和R08 3颗GLONASS卫星站间IFCB实时估值的时间序列。试验数据观测时段2020年DOY 119 UTC 06∶00—06∶30，采样间隔为1 s，每5 min进行一次站间IFCB重新初始化解算。由图6可知，站间IFCB估值通过约30 s序贯最小二乘平差迭代即可获得分米级的精度，1 min内完成收敛。因此，将迭代1 min的站间IFCB估值用于修正GLONASS伪距观测值具有可行性。

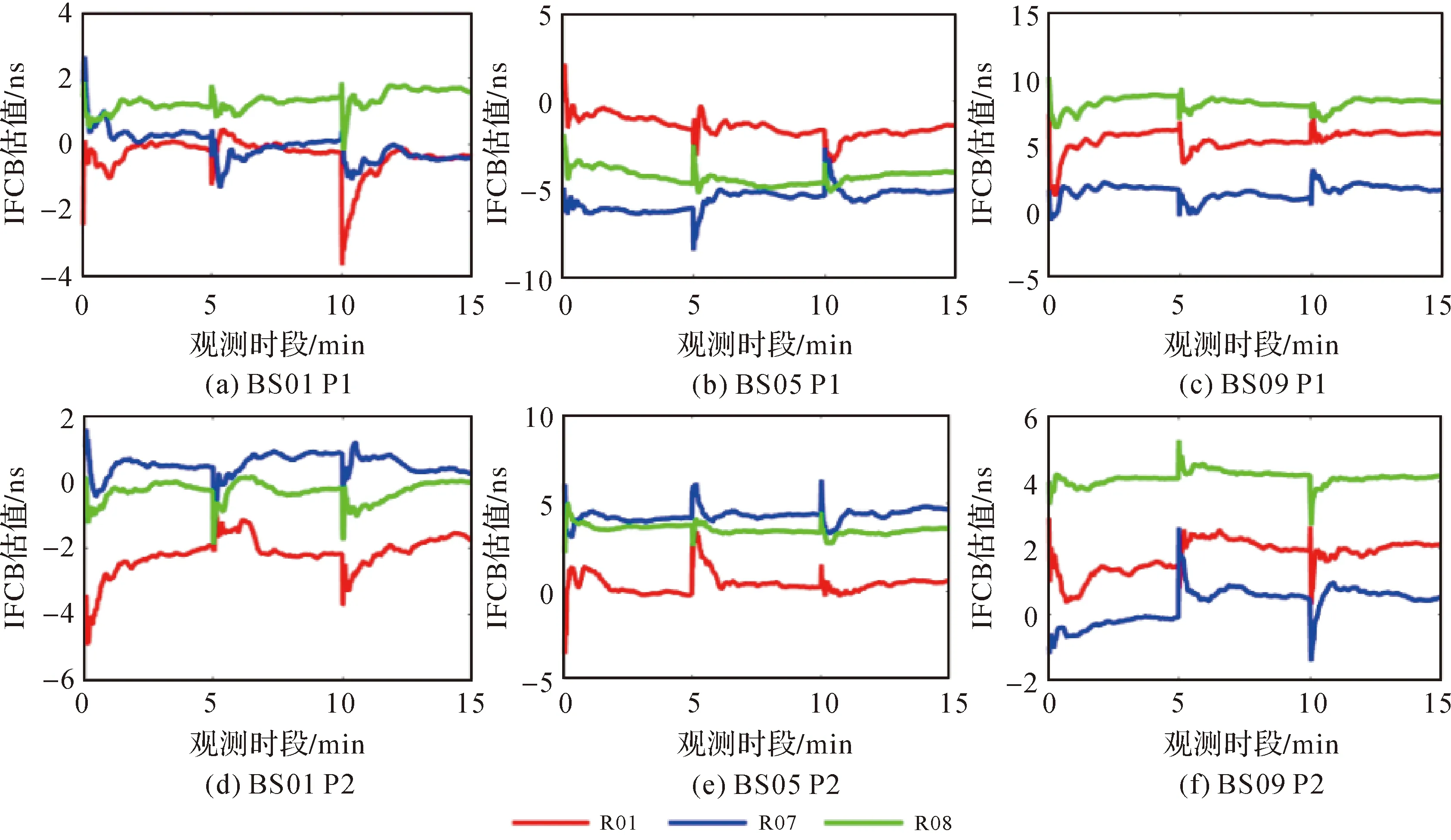
图6 基线BS09GLONASS卫星站间IFCB实时估值时间序列Fig.6 Time series of GLONASS inter-station IFCB estimates on baseline BS09

采用G、GR uc-IFCB和GR rtc-IFCB 3种模式分别进行RTK定位解算。图7和图8给出了基线BS01和BS09的GLONSS和GPS卫星模糊度浮点解偏差。短基线RTK场景下，忽略了双差大气延迟的影响，GLONASS站间IFCB在解算过程中主要归入残差向量，需要通过更长时间的滤波，才可以获得准确的模糊度浮点解。因此，短基线BS01，未改正站间IFCB时，GLONASS卫星需要约6 min时间才能获得稳定的高精度模糊度参数浮点解，站间IFCB实时改正算法可将收敛时间缩短到3 min以内；如图8左侧图所示，改正站间IFCB可以明显加快GPS卫星模糊度浮点解收敛。在中长基线RTK场景下，需估计电离层和对流层延迟参数，由于电离层参数与站间IFCB的强相关性，导致电离层参数估值产生偏差，进而影响模糊度浮点解。修正GLONASS伪距观测值对中长基线RTK定位至关重要，可有效消除估计参数偏差，改善模糊度准确度，提高模糊度固定率和RTK定位性能。

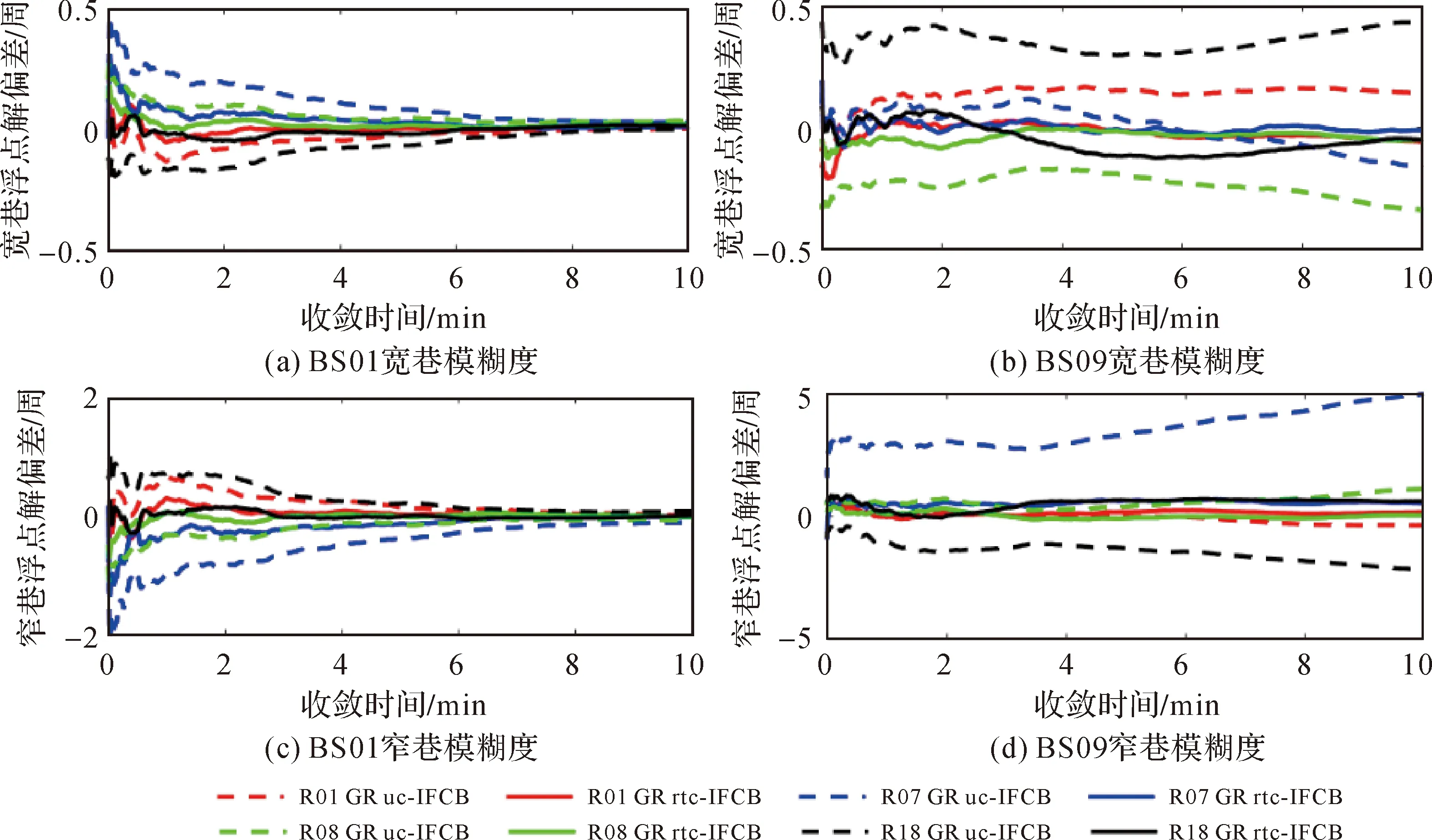
图7 GLONSS卫星宽巷和窄巷模糊度浮点解偏差Fig.7 The bias of GLONASS satellite wide-lane and narrow-lane ambiguity float solutions

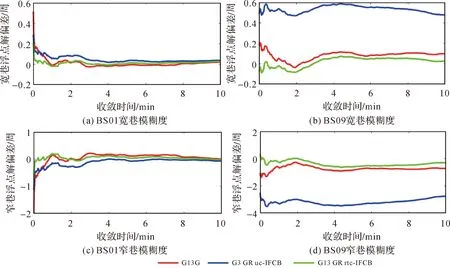
图8 GPS卫星G13宽巷和窄巷模糊度浮点解偏差Fig.8 The bias of GPS satellite G13 wide-lane and narrow-lane ambiguity float solutions

图9统计了所有基线不同模型RTK解算模式下的收敛时间。本文将RTK定位水平方向偏差稳定在小于0.1 m作为判定收敛完成的阈值[14,27]。基线BS04、BS08和BS09受站间IFCB的影响，GPS/GLONASS组合RTK定位收敛速度较单GPS RTK定位变慢。站间IFCB实时改正后，GPS/GLONASS组合RTK收敛速度明显加快，大部分基线的收敛时间减小到单GPS RTK的60%以下，解决了因引入GLONASS卫星导致异质基线收敛速度降低的问题。站间IFCB改正算法对同质基线BS10 GPS/GLONASS组合RTK定位收敛时间的影响很小。基线BS06因流动站数据质量较差，定位收敛速度较慢，单GPS RTK需要约90 s完成收敛。

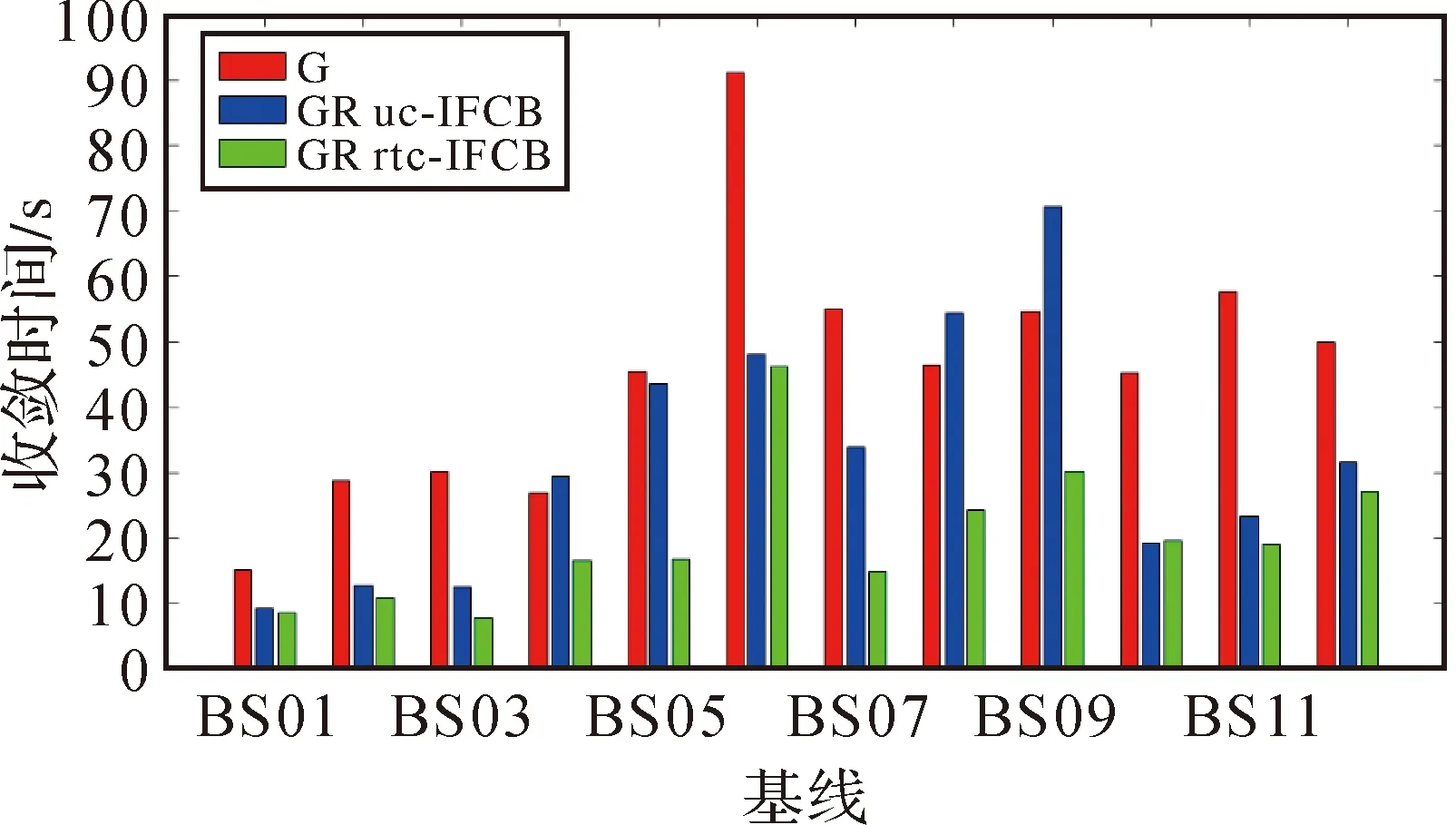
图9 不同模式RTK解算的收敛时间Fig.9 Convergence time of RTK positioning solutions

采用式(18)和式(19)统计模糊度固定成功率Psuc和正确率Pcor

(18)

(19)

式中，namb为解算中模糊度参数的总数；nfixed为固定的模糊度参数个数；ncorrect为正确固定的模糊度参数个数。

站间IFCB改正能够显著提高中长距离基线的GPS和GLONASS卫星模糊度固定成功率和正确率，如图10和图11所示。站间IFCB导致基线BS09的GLONASS卫星窄巷模糊度固定成功率低至52%，改正后提高到约90%，模糊度固定正确率也从85%提高到96%。短基线(BS01—BS04)，双差大气延迟量级较小，可忽略，模糊度固定容易，改正站间IFCB对模糊度固定的影响不大。但是，当站间IFCB量级很大时，改正站间IFCB对提高模糊度固定效率十分必要。

图10 RTK定位解算模糊度参数固定成功率Fig.10 The successful fixing rates of ambiguity parameters in RTK solution

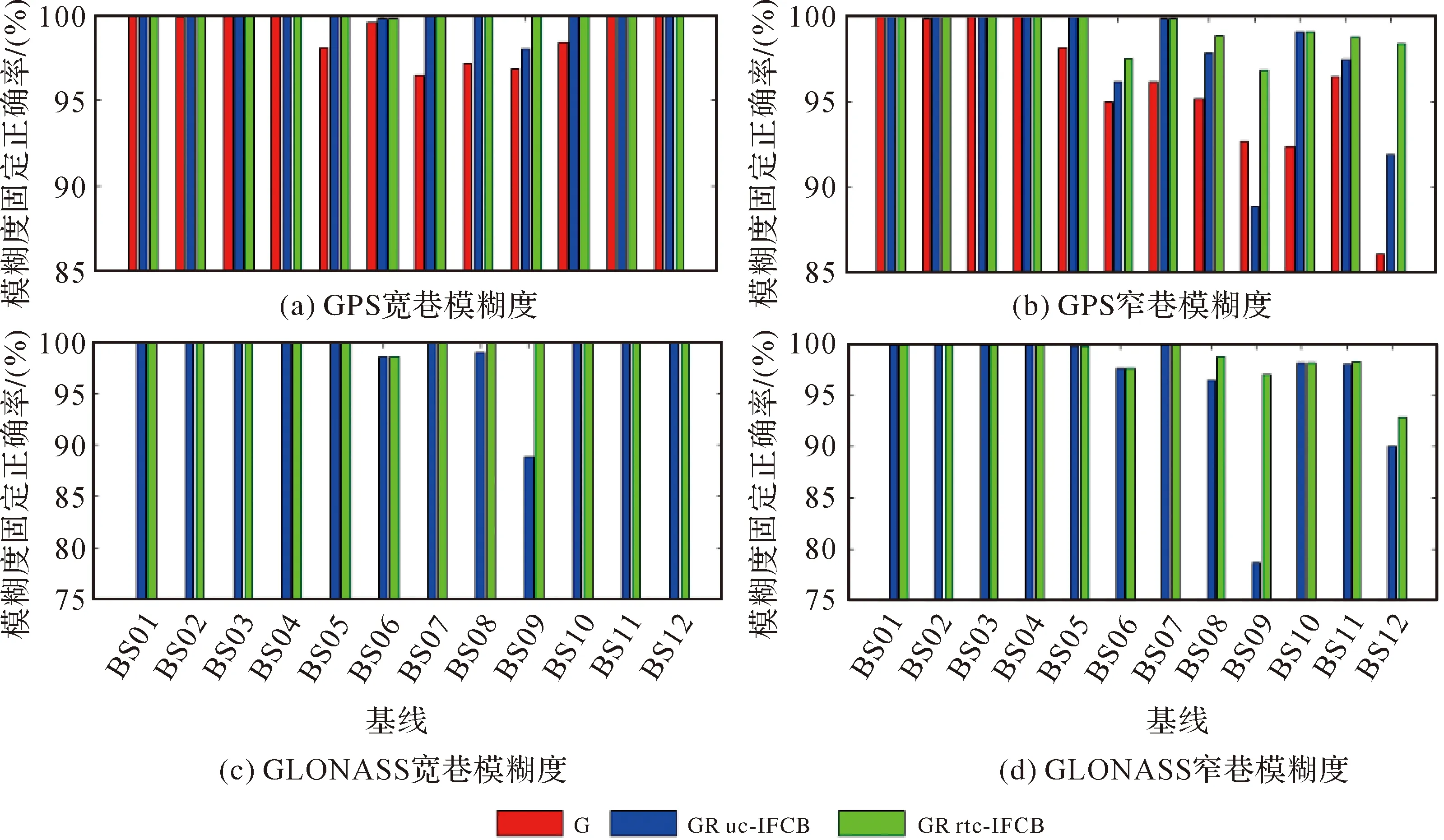
图11 RTK定位解算模糊度参数固定正确率Fig.11 The correct fixing rates of ambiguity parameters in RTK solution

采用分步部分模糊度固定策略获得RTK固定解，统计其首次固定时间、固定解比率和固定解偏差RMS，如图12和图13所示。以EPN网站发布的坐标值作为参考站和流动站坐标的真值。与上文试验结果类似，站间IFCB改正算法能够明显改善中长距离基线GPS/GLONASS组合RTK定位性能。相比单GPS，站间IFCB导致基线BS09的GPS/GLONASS组合RTK首次固定时间变长且固定解比率降低。进行站间IFCB改正后，首次固定时间统计值从9.2 s提高到2.1 s，固定解比率从84.5%提高到97.9%。由于短基线RTK能够实时获得固定解，站间IFCB改正对定位结果的影响不明显。改正站间IFCB后，模糊度固定率提高，RTK固定解的定位偏差也有不同程度的改善。如基线BS12东北天方向的定位偏差RMS分别从2.5、2.8、6.1 cm提高到2.3、2.4、5.0 cm，其中高程方向改善率达18%。

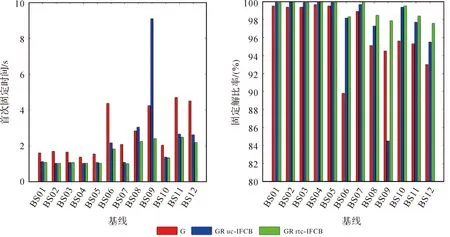
图12 RTK定位首次获取固定解时间和固定解比率Fig.12 Time to first fixed and rates of RTK fixed solutions

图13 RTK定位固定解ENU方向的RMSFig.13 Positioning bias RMS of RTK fixed solutions on E/N/U direction

3 结 论

本文提出了一种不依赖测站设备信息的站间IFCB实时估计方法，对GLONASS卫星各频段站间IFCB进行了特性分析，并将站间IFCB实时改正算法应用于GPS/GLONASS组合RTK定位，获得了以下结论：

(1) 站间IFCB单天解具有一定的稳定性，20 d内单天解估值的标准差小于0.3 ns，同一条基线不同频段站间IFCB的量级存在很大差异，可达几个纳秒。站间IFCB会导致异质基线RTK解算模糊度固定失败，甚至个别基线GPS/GLONASS组合定位的性能比单GPS差。

(2) 将站间IFCB实时估计算法用于GPS/GLONASS组合RTK定位，能够显著改善GPS/GLONASS组合RTK定位性能。对于受站间IFCB影响严重的基线，算法能够将GLONASS卫星窄巷模糊度固定成功率从52%提高到90%以上，东北天方向的定位偏差RMS分别从2.5、2.8、6.1 cm提高到2.3、2.4、5.0 cm。