顾及空间分布与注记相关性的点要素注记配置算法
曹 闻,彭斐琳,童晓冲,戴浩然,张 勇
1. 郑州大学地球科学与技术学院,河南 郑州 450000; 2. 信息工程大学地理空间信息学院,河南 郑州 450001; 3. 郑州众合景轩信息技术有限公司,河南 郑州 450000
随着大数据时代的到来,人们对大数据中所蕴含的内在机理和高价值信息有着迫切的需求和期待,数据可视化成为大数据分析不可缺少的工具[1-2]。在数据可视化中,各行业数据经常利用地理信息技术将其整合到地理空间上进行分析和表达,因此,地理空间数据可视化是大数据分析的重要基础,通常以地图的形式展示[3-4]。注记作为可视化产品中重要组成部分,是最直观传递信息的要素[5],由此,提升注记质量成了研究的热点和难点。
数据可视化中的空间对象分为点、线、面、体等形式[6-9],其中,点要素注记的自动配置问题(point-feature label placement problem,PFLP)最为复杂,已被证明是NP-hard问题[10]。为了解决在庞大规模的组合优化问题中寻找最优解的难题,国内外学者对此进行了大量的研究。元启发式算法是一种使用高级策略来探索空间的方法[11],能在有限的时间内找到一个较好的近似最优解,目前已被广泛应用到点要素注记配置问题的研究中,如禁忌搜索、模拟退火算法、遗传算法和蚁群算法等[12-15]。大部分学者通常以改进元启发算法为主,将所有点要素视为一个整体进行解算,并未考虑到点要素之间的独立性,而随着点要素数量的增多,组合优化的规模呈爆炸式增长,导致算法求解的效率极低及求解质量不佳。因此,有部分学者利用点要素的空间分布特征来指导注记配置问题的解算,主要分为两类:一是采用聚类分组的方法对点要素进行分析和求解。文献[16]提出利用最短距离聚类的方式分析点要素空间分布特征的设想。文献[17—18]通过构建点要素冲突图和拉格朗日松弛法进行聚类,将其划分为多个数据簇进行求解。文献[19]利用基于密度的聚类方法(density-based spatial clustering of applications with noise,DBSCAN)将问题空间划分成多个子问题空间,进而利用蚁群算法对子问题进行求解。该类算法虽然有效地缩短了注记配置的计算时间,提高了注记效率,但其聚类的过程忽略了点要素注记之间的影响,从而导致聚类得到的不同子数据集之间的独立性方面存在着模糊性和粗差。二是通过规划注记次序指导注记配置过程的方式来优化注记配置结果。文献[20]指出利用Voronoi图描述点要素的空间分布特征和要素在注记配置过程中的相互影响性,通过规划自由度来指导注记配置沿着简单、高效和高质量的方向进行。文献[21]提出周围要素较为密集且注记候选区域面积较小的点要素优先注记,对注记配置的顺序进行了优化。该类算法利用注记次序指导了注记配置过程,虽然能在一定程度上提高注记配置质量,但在空间分布稠密的情况下易受到点要素注记间强干扰性的影响,从而导致算法求解更易落入局部最优陷阱。
针对上述问题,本文通过挖掘点要素数据集的整体空间分布特征、局部空间分布特征和注记相关性,提出了一种顾及空间分布和注记相关性的点要素注记配置算法,并通过试验证明该算法的有效性。
1 算法原理
稠密型点要素的注记自动配置问题主要受限于注记效率和质量,针对该问题,本文考虑到点数据集的空间分布特征和注记间的相关性,设计了一种注记关联度模型,继而对点要素数据集进行空间聚类分析和注记次序规则制定,最后采用多层次元启发算法求解注记配置问题的近似最优解。
1.1 注记关联度模型
1.1.1 注记候选位置模型
注记候选位置模型的选择是注记配置的重要基础之一[22-23],直接影响着注记配置的质量和效率。为了增加固定位置模型的灵活性和降低滑动模型的运算量,采用文献[19]提出的多级多方位模型,如图1所示,可通过细化参数半径r和等分角θ两个参数提升空间利用率,但势必带来较大的运算量而降低注记效率。因此,综合考虑注记配置质量和运算时间两方面的平衡,本文选择等分角θ为45°,并使用优先级度量构建8位置模型。其中,图1中的数字从小至大表示注记位置优先级由强至弱的程度,同时为了注记美观性,将点要素的符号外接圆加入多级多方位模型中,即要求点要素符号化区域半径r1要小于注记多级半径r,实线椭圆和虚线矩形分别为不同位置、字符高度、字符串长度所形成的外接椭圆和最小外接矩形。

图1 多级多方位注记候选模型Fig.1 The multi-levels and multi-orientations label candidate location model
点要素注记自动配置算法通常是以某种规则选择不同的注记候选位置得到近似最优解,在此过程中每个已注记点要素的位置会直接影响到随后点要素的注记位置,因此如何利用其多样性和互干扰性指导算法求解是值得重点关注的问题。
1.1.2 注记关联度规则
在点要素注记配置问题的求解过程中,注记间的干扰会导致算法极易陷入局部最优陷阱和求解效率低下。由于注记最小候选外接矩形包括了点要素所有的候选位置,因此可根据注记最小候选外接矩形为计算基础设计相应的注记关联度规则量化不同点要素在注记配置过程的相互干扰关系。
假设图面待配置点要素的集合为P={p1,p2,…,pN},点要素pi和pj的最小候选外接矩形分别为Ri和Rj,定义一个二进制变量αij表示点pi和pj之间是否存在相互干扰性。若αij=0,表示点要素pi和pj在注记配置过程中不存在干扰性,即Ri∩Rj=φ,不需考虑二者注记的先后顺序;若αij=1,表示点要素pi和pj间具有干扰性,需考虑二者具体注记对注记配置的影响,如图2中点要素pi和pj,Ri∩Rj≠φ,表示其最小候选外接矩形存在相交的部分,则该相交部分定义为注记影响面Aij,即Aij=Ri∩Rj。显然,二进制变量α和注记影响面A均具有对称性,即αij=αji和Aij=Aji。

图2 注记影响面Fig.2 Label influence surface pattern
考虑到点要素间的干扰性将直接影响到注记配置的效率和质量,依据点要素最小注记外接矩形之间的关系,定义注记支持度η和注记关联度ξ两个变量对点要素注记间的干扰程度进行量化描述,以此挖掘点要素数据集合的局部空间分布特性和注记相关性。
1.1.2.1 注记支持度ηi
注记支持度是指任一点要素pi在注记配置过程中与其注记最小候选外接矩形相关的其他点要素的个数,记为ηi
(1)
注记支持度ηi反映了点要素pi注记后影响到数据集中其他点要素的个数,数值越大说明更多的点要素需根据pi的注记位置进行调整,以避免注记出现重叠和冲突问题。根据注记支持度ηi的物理意义,可将所有参与注记配置的点要素概括为独立点、直接关联点和间接关联点3类。
(1) 独立点。对于点要素pi,如果相对于其他任意点要素pj(i≠j)均存在Ri∩Rj=φ,则称pi为独立点,如图2中pt和ps。独立点形成的数据集合称为独立点集,记为ΩI(ΩI⊆P)。在注记配置的过程中,独立点注记位置的随机性选择会降低算法寻优速度,因此可根据注记位置的优先性和图面美观性直接注记。

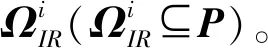
注记支持度ηi通过统计点要素pi直接关联点的个数来描述其局部空间分布特性,数值越大表示其局部空间分布越稠密,将其视为优先注记点就意味着其他关联点要素注记位置的可选择性将减小,导致注记配置质量不佳。
1.1.2.2 注记关联度ξi
注记支持度ηi虽然描述了点要素的局部空间分布特征,但忽略了存在关联性点要素间的相关性,点要素pi和pj间注记影响面Aij和Aji相等,由于两点注记最小候选外接矩形不同,因此二者的互干扰程度也将不同。如图3(a)所示,点要素pj优先注记后,注记影响面Aij覆盖点要素pi候选区域中的8个区块;而图3(b)中点要素pi优先注记后,注记影响面Aji覆盖点要素pj候选区域中的4个区块。因此需引入注记关联度ξi描述点要素注记间的相关性。

图3 注记关联度原理Fig.3 Label relevance principle
假设点要素pi优先注记对点要素pj的后续注记位置的干扰概率Pij可定义为
(2)

(3)
式中,ωk表示干扰概率Pij等间隔区间对应的权值,其中0<ω1<…<ωk<…<ωM。注记关联度ξi描述了点要素pi优先注记后对其局部区域内其他点要素的干扰程度,量化了注记间的相关性。
综上所述,通过注记支持度ηi和注记关联度ξi两个参数制定点要素pi的注记关联规则,以此描述点要素pi的局部空间分布特征和注记互相关性,从而为注记配置求解提供先验辅助决策信息。
1.2 基于注记关联度模型的空间分布特征分析
稠密型点要素数据集的空间分布是较为复杂的,会存在一定数量的独立点或不相关的多个子数据集,而这些点要素和子集在整体答解时,会引入较大的模糊性和干扰性,同时注记候选位置模型的多样性会使注记组合规模随点要素数量的增加呈指数型增长,从而导致算法求解质量不佳和效率降低等问题,其根本原因在于忽略了点要素数据集的整体空间分布特征。
空间聚类算法能够发现空间实体对象的空间聚集模式,通常被用来揭示其内部分布规律和空间结构特征,在地理空间数据挖掘领域得到了广泛应用。其中,DBCSAN算法能较好地应用于点要素注记配置研究中[19],有效降低问题求解的复杂度和提升注记配置的效率。DBSCAN空间聚类算法是通过判断点是否落在另一点搜索邻域范围内确定两点之间是否存在关联性,其关键在于搜索半径和核心点判断阈值两个参数的确定,在注记配置问题中的搜索半径和核心点判断阈值通常选择点要素注记的候选区域和1。如图4(a)所示,点4、6、7、8被归为独立点,但实际其注记存在互相干扰性,容易出现注记叠加的现象。为了适应点要素注记配置的特点,利用注记关联度模型中的直接关联点和间接关联点两个集合进行递归类推最终得到互不关联的独立点集ΩI和M个子数据集Ωk,k∈[1,M],继而消除具有独立性点集对注记配置求解产生的模糊性和干扰性,如图4(b)所示,独立点集可根据注记位置优先性和图面美观性直接注记,而关联点集则视为一个局部整体进行问题求解,从而全局问题转换为多个局部问题提升注记配置解算效率和注记质量。

图4 空间聚类算法Fig.4 Spatial clustering based on association model
空间聚类算法主要是对点数据集的空间聚集性进行数据挖掘和分析,虽然降低了互不关联的数据集对注记配置解算的干扰性和模糊性,但由于没有充分利用子集中内部点要素间的干扰性,将导致无法获得更佳的注记质量。
1.3 基于注记关联度模型的次序规则
对关联点子数据集进行注记配置是旨在有限的空间内获取最大化可注记数量,而点要素注记之间的干扰性其实反映的是这些点要素之间的空间竞争关系,因此该注记配置求解问题也可被视为注记的取舍问题。在注记配置求解过程中,点要素注记的取舍是根据之前的注记结果来判断是否存在合适的空间配置注记,同时该注记也会影响到之后点要素能否注记。注记配置算法通常以随机次序进行注记,忽略了点要素数据集的内在空间结构和秩序信息,从而无法得到更加合理的注记结果。
注记关联度模型通过定义注记支持度ηi和注记关联度ξi两个参数分别描述点要素pi的局部空间分布特征和其直接关联点注记间的相关性,本文依次按照两个参数值增序对点要素进行排序,构建基于增序注记关联度模型的次序规则,其中,注记支持度ηi对点要素间的干扰程度具有强相关性,而注记关联度ξi具有弱相关性,因此基于增序注记关联度次序可表示为:对于不同规模的点要素集合,先以注记支持度ηi从小到大对所有点要素进行排序;然后对相同注记支持度ηi的点要素再按照注记关联度ξi从小到大排序;最后对两个参数均相同的点要素按照随机的方式进行排序。如图5所示,增序注记关联度模型较降序注记关联度模型的注记次序规则,可以有效降低优先注记点要素对后续待注记点要素的干扰性,指导着注记配置过程,提高算法的寻优速率,从而使近似最优解更加逼近最优解。

图5 不同次序规则结果Fig.5 Labeling cases for different labeling orders
1.4 基于注记关联度模型框架的注记自动配置
注记关联度模型框架(annotation association model framework,AAMF)是通过基于注记关联度模型的DBSCAN空间聚类算法和次序规则挖掘点要素的空间分布信息和注记相关性,进而对注记配置算法求解进行指导。基于注记关联度模型框架下的注记配置通过制定注记质量评价函数、冲突检测方法和多层次元启发算法等环节获取更具合理性的注记配置结果。
1.4.1 注记质量评价函数
注记配置旨在获得最大化清晰、美观和可读的无冲突注记数目,因此本文参照文献[24—25]中的方法以无冲突的注记数因子Fo、注记位置的优先性因子Fp和注记的关联性因子Fa构建注记质量评价函数F
F=λ1Fo+λ2Fp+λ3Fa
(4)
式中,λ1、λ2、λ3分别为各因子对注记质量影响力的占比系数,一般而言λ1=0.5,λ2=0.3,λ3=0.2,但其中关联性与人眼能识别出的最小距离有关,不能准确衡量歧义距离,因此设置λ3=0。设质量评价函数较小对应着较好的注记配置结果,因此点要素注记配置的目标是获得最小化质量评价函数值。
1.4.2 注记冲突检测
点要素注记配置过程中,要求注记之间不可出现重叠或压盖现象,因此,在注记配置的过程中需制定注记冲突检测方法加以解决。目前常用的空间索引方法主要有R树空间索引和格网空间填充等多种方法[26-27]。R树索引是以规则矩形的方式进行碰撞检测,对于不规则的地物要素与存在旋转等情况存在着查询不准确的缺点,浪费大量的图面空间。格网空间填充索引是使用一种行排序的空间曲线填充方式进行编码[28],原理简单易懂,在冲突碰撞检测过程中只需要判断某点注记所在位置的格网是否被占用,相当于一个局部小范围的遍历寻址,同时对于不规则的地物要素有较强的适应性和稳健性。因此,本文考虑到矢量背景要素符号的不规则性及点状要素的注记旋转等因素,采用格网空间填充的索引方式进行冲突检测。
1.4.3 多层次元启发式算法
点数据集的空间分布通常疏密不均,经空间聚类后关联点子数据集中的点要素数量不均匀。蚁群算法、模拟退火算法和遗传算法常应用于解决点要素注记配置问题,但当关联点集中点要素数量较少时,直接求解则会导致容易陷入局部最优等问题,因此需要针对不同数量的点要素数据集设计多层次元启发算法提升其普适性和稳健性。
多层次元启发算法是依据关联点集的大小采用不同搜索策略的元启发式算法进行求解。首先根据数据集中点要素的数量定义一级、二级和三级3种等级的数据集,同时设置两个阈值分别为:低阈值δ1和高阈值δ2(δ1,δ2∈N+,δ1<δ2),当点要素数量n<δ1(δ1∈[1,10]),即为一级数据集。利用注记无冲突性的要求,采用文献[14]中注记冲突调整的方式进行注记配置。针对具有注记冲突的点要素更新注记方向的选择,能更快地获得较优的注记结果。点要素数量δ1

表1 元启发式参数Tab.1 Metaheuristic parameter
2 试验与分析
为了验证本文所提注记关联度模型对点要素注记自动配置算法的优越性,利用网络爬虫技术从某地图网站获取郑州市兴趣点POI数据,以其随机生成3000和6000点规模的数据集合为试验数据,采用模拟退火算法、蚁群算法和遗传算法讨论和分析反映注记关联度模型框架对提升点要素注记自动配置算法效率和质量的意义。试验与分析中的所有算法均通过Visual C++编程实现,试验环境的处理器和内存分别为Intel(R) Core(TM) i5-8500 3.0 GHz和8 GB。
2.1 顾及空间分布和注记关联性点要素注记配置对比试验
点要素注记自动配置的质量和效率主要受到点要素数量和注记方向多样性的影响。本文依据数据集的空间分布特征与注记相关性构建基于注记关联度模型的算法框架AAMF,并应用于元启发式算法来进行点要素注记配置试验,主要包括基于注记关联度模型框架下的模拟退火算法AAMF-SA、遗传算法AAMF-GA和蚁群算法AAMF-ACA,考虑到数据集空间分布的稀疏稠密特征对基于注记关联度模型算法效果的影响,设计在常用的8种注记密度ρ为5%、10%、15%、20%、25%、30%、35%和40%下,比较AAMF算法与传统算法的优劣性。试验以所有的点要素视为同一细节层级为前提,采用模拟退火算法、遗传算法和蚁群算法比较随机次序规则R1、基于降序注记关联度模型的次序规则R2和基于增序注记关联度模型的次序规则R3的试验结果,讨论与分析基于注记关联度模型的次序规则在不同元启发式算法下的有效性。每组试验重复10次取平均值,点要素数量低阈值δ1与高阈值δ2分别为7和100,参数r、r1和注记字体分别设置为10、5和12像素。记录每组试验的耗时T和注记质量评价函数值E,试验结果见表2—表7和图6、图7。

图6 算法注记配置结果Fig.6 Labeling result of algorithm

图7 注记结果细节对比Fig.7 Detailed comparison of labeling results

表2 注记密度为5%~20%模拟退火算法的试验结果统计Tab.2 The statistical results of SA with label density range from 5% to 20%
由表2、表3可知,不同的规则算法对注记配置结果产生了较大的影响。首先,从次序规则上来说,基于增序注记关联度模型的次序规则R3的质量评价函数值相较于随机次序规则R1降低3~8.5,相较于基于降序注记关联度模型的次序规则R2降低6~15.8,规则R3的结果均优于规则R1和R2;其次,AAMF-SA算法比SA算法求解的效率平均提升16.78%,且评价函数值降低了12.28;通过试验分析可以看出,AAMF-SA取得了较好的注记配置结果和注记效率。

表3 注记密度为25%~40%模拟退火算法的试验结果统计Tab.3 The statistical results of SA with label density range from 25% to 40%
由表4、表5可知,基于增序注记关联度模型的次序规则R3比随机次序规则R1的质量评价函数值平均降低5.95、比基于降序注记关联度模型的次序规则R2平均降低12.82,由此可见,次序规则R3优于规则R1和R2,提高了注记配置质量。AAMF-GA算法比GA算法求解效率平均提高18.1%;其评价函数值平均降低9.2。其中,在注记密度为5%下的6000点规模试验中,AAMF-GA的评价函数值比GA降低32.8,注记质量大幅度提升,但其注记效率比GA降低了4.97%,这是因为空间聚类算法将大规模单一数据集分成了若干个子数据集,减少了要素注记间的干扰性,使得每个子数据集求解时不断地进行迭代优化从而提升了注记质量,同时也增加了算法的迭代时间,由此损失的效率是可以接受的。

表4 注记密度为5%~20%遗传算法的试验结果统计Tab.4 The statistical results of GA with label density range from 5% to 20%

表5 注记密度为25%~40%遗传算法的试验结果统计Tab.5 The statistical results of GA with label density range from 25% to 40%
蚁群算法试验结果见表6、表7。首先,AAMF-ACA算法比ACA算法效率平均提升17.70%,评价函数值平均降低7.71;其次,基于增序注记关联度模型的次序规则R3比随机次序规则R1的质量评价函数值平均降低了8.11,同时,比基于降序注记关联度模型的次序规则R2平均降低15.6。试验分析表明,AAMF-ACA能有效提升注记配置效率和注记配置质量。

表6 注记密度为5%~20%蚁群算法的试验结果统计Tab.6 The statistical results of ACA with label density range from 5% to 20%

表7 注记密度为25%~40%蚁群算法的试验结果统计Tab.7 The statistical results of ACA with label density range from 25% to 40%
综上所述,基于注记关联度模型框架能较好地应用于模拟退火算法、遗传算法和蚁群算法,并取得了注记效率和注记质量的提高。基于增序注记关联度模型的次序规则R3取得了最好的配置优化效果,其次是随机次序规则R1,基于降序注记关联度模型的次序规则R2配置结果质量最差。结合表2—表7试验结果统计进行分析,首先,在注记密度为5%~40%下,规则R3比规则R1注记配置的质量评价函数值分别降低3.0~5.7、5.0~8.4、6.9~8.5、4.6~9.2、6.0~8.9、5.2~10.9、5.5~9.8、7.3~9.4,比次序规则R2降低5.9~10.7、8.6~15.4、13.0~17.5、11.4~18.2、13.1~17.6、13.4~17.3、14.8~17.6、15.1~17.5。数据分析表明,随着注记密度由5%至40%,注记次序规则R3与R1、R2的差值由小逐渐增大,这是因为当数据集空间分布较为稀疏时,大部分的点注记候选区域只影响少量个别其他点注记候选区域,无论采用哪种注记次序,注记都有较大的可能性找到空间放置,因此,在这种情况下,3种规则的注记配置结果区别较小。当数据集空间分布较为稠密时,注记间的冲突性和关联性增大,规划以增序注记关联度模型的次序令关联性较小的点要素优先注记,能大幅度地减少已配置的注记对待配置注记的影响,对注记配置的结果有着较好的优化效果。其次,新算法相较于传统元启发式算法效率平均提高了28.92%、19.23%、16.47%、16.42%、14.30%、14.59%、13.79%、10.41%,且质量评价函数值平均下降了26.5、13.4、8.7、6.1、4.5、4.1、3.5、2.5。由此可见,注记效率和质量的提升幅度有着明显的下滑趋势,这是因为注记密度变大,数据集的空间分布较为集中,空间聚类后获得最大子集的点要素数量与整体数据集相差无几,空间聚类算法已经不能大幅度地减少干扰性和降低计算复杂度,同时又增加了聚类这一过程的耗时,从而降低了注记效率和质量的提升,因此,当点要素空间分布较为稠密时,空间聚类算法对注记配置的作用会减小。
图6和图7展示了对6000点要素使用AAMF算法与传统算法得到的同一区域注记结果局部对比图和细节对比图。在本组注记配置结果中,AAMF算法获得的无冲突注记数总计3218个,在图6中展示的局部区域有256个注记,传统算法获得的无冲突注记数总计3065个,在图6中展示的局部区域212个注记,AAMF算法取得了153个注记的提升。图7(a)和7(b)分别是图6(a)和图6(b)的典型细节注记结果示例,由该图可以看出,图7(a)中的点注记方向和注记数量更有优势,其基于注记关联度模型的空间聚类算法与注记次序规则,既降低了组合优化问题的复杂度又提高了每个点要素可注记概率,取得了较好的注记效果。而图7(b)注记数目和注记方向较AAMF算法的注记配置结果有一定的差距,这是因为其整体求解方式不能反映单个点要素或者某块独立数据集的注记配置的需求,且注记的随机性无法为配置过程提供先验辅助决策信息,令注记配置的结果质量不佳。因此,本文提出的AAMF算法相较于传统算法更有优势。
2.2 与MapLex智能标注系统的对比试验
为了对比新算法与MapLex智能标注系统的注记质量,采用基于关联度模型框架的模拟退火算法与ArcGIS 10.5版本下的MapLex注记配置进行对比,由于MapLex无法统计注记方向,仅将无冲突注记个数作为比较标准,试验统计结果见表8。试验参数r、r1和注记字体分别设置为2、2和12像素,MapLex系统中r、r1和字体设置为2、2和9磅。

表8 试验结果统计Tab.8 The statistical result of the experimental data
由表8的试验统计结果可知,新算法获得的无冲突注记数均比MapLex智能标注系统多,注记配置质量更为合理,但新算法在时间效率方面仍然需要得到进一步提高。
3 结 论
本文针对稠密型点状要素注记自动配置问题,通过构建注记关联度模型对点要素数据集的全局空间分布特征、局部空间分布特征以及注记之间的相关性进行表达和描述,进而利用基于注记关联度模型的多层次元启发式算法求解点要素注记配置的近似最优解。其中,用于描述点要素数据集整体空间分布特征的空间聚类算法对稀疏性点要素数据集的注记配置更具优势,而用于描述局部空间分布特征和注记相关性的次序规则对稠密性点要素数据集的注记配置更具优势。新算法虽然通过空间数据挖掘在注记配置效率和质量上得到了明显提升,但仍然存在不足之处:①注记关联度模型缺乏图面空白区域指导点要素具体注记方向的能力,需进一步地提升注记配置算法的效率和质量;②新算法使用格网空间填充方法虽然可有效解决不规则对象和旋转等复杂环境下的注记冲突检测问题,但随着注记范围的增大,会产生占用内存空间过大和局部寻址效率低下的问题;③需进一步研究如何在质量评价函数中根据人们视觉制定更为合理的歧义性因子,以增强注记的可读性和视觉美观性。

