移动机器人SLAM位姿估计的改进四元数无迹卡尔曼滤波
赵玏洋,闫 利
武汉大学测绘学院,湖北 武汉 430079
在传统测绘产业数据获取和数据处理模式中,大量重复性的人工工作还是占据主导地位,这种方式不仅效率极低,而且难以达到精度的要求,逐渐无法满足智能化测绘阶段时空信息获取与应用需求。随着移动机器人技术的广泛成熟以及智能化程度的提高,智能化测绘技术将改变目前数字化测绘以人为中心的方式,给测绘领域提供新的活力,成为未来发展的必然趋势,突破原有数字化测绘由人为因素带来的环境不可及和效率上的瓶颈。智能化测绘产业将以自主化、实时化为技术目标,建立结合主动探索、实时感知和智能决策的技术体系。
近年来,随着机器人技术的发展,机器人已经被广泛应用于实际生产领域中,特别是功能强大的移动机器人在测绘领域中所扮演的作用越来越大。随着移动测量技术走向成熟,特别是无人机测量、车载移动测量等的诞生,更是在一定程度上解决了动态测量技术问题[1-2]。如今,智能科技产业的发展已经在社会生产和生活中掀起了重大的变革,拥有自主化、实时化能力的移动机器人为测绘产业带来了巨大的发展机遇,利用机器代替人并完成测量行为的自主移动机器人也将是今后智能化测绘产业的发展方向。
自主移动机器人具有明显的智能化和先进性特征,可以实现对于周围信息的感知和处理,自主做出决策和规划,并实现既定的移动目标[3]。国外部分高校以及研究机构很早开始了相关的研究,在20世纪60年代,斯坦福大学首次发布了机器人Shakey,其具备了一定的自主决策功能,引发了较大的关注,可以实现路径规划,并且在不同的环境中适用性良好[4]。进入21世纪,在机器学习以及大数据等技术持续发展的背景下,这些新技术被应用于移动机器人的设计中。其中LAAS团队研制的HILARE机器人[5]配备了视觉相机和激光测距仪等传感系统,可以在已知场景内实现路径规划和导航功能。移动机器人的发展从最初的工业机器人扩展到面向服务的自主移动机器人,在医疗保健、文化娱乐等生活方式中有很大的需求,显示出较大的应用前景。Massachusetts Institute of Technology的Wheelesley、德国Vamors-P和Caravelle systems、Carnegie Mellon University的CMU漫游者也在移动机器人领域有较高水平的研究成果[6]。
移动机器人在未知环境下从初始点开始运动到既定目标的过程中,需要准确获取自身的位置以及环境中障碍物的位置。文献[7]针对机器人的导航,将其总结为两个问题,分别是“我处于何地?”“周围环境如何?”,二者实际上对应着定位、建图的过程。1995年,文献[8—10]提出“SLAM”一词,并给出了移动机器人SLAM的基本技术框架。
SLAM根据传感器类型的不同,可主要分为视觉SLAM[11-13]及激光SLAM[14]。移动机器人SLAM的研究主要包括数据关联[15]、环境特征提取与表示[16]、目标检测[17]、闭环[18]等。移动机器人SLAM问题中存在许多不确定因素,例如与观测模型以及所处环境的不确定性等因素有关[19],由此逐步出现了基于概率的SLAM算法,具体可以将其划分为不同的类型[20],例如有基于EKF的SLAM算法、基于期望最大化(EM)的SLAM算法等。
卡尔曼滤波(KF)算法用状态向量表示移动机器人的姿态和特征在地图上的位置。在此算法中认为是线性系统,噪声以及状态均满足高斯分布,然而由于存在显著的线性误差,因此文献[21—22]设计了EKF算法,该算法能够实现对于非线性系统的逼近。
为了减少EKF-SLAM算法的计算量,文献[23]设计了无迹卡尔曼滤波(UKF)。在此方法中无须对Hessians矩阵进行计算,使用Sigma点集来近似目标状态的后验概率密度。但UKF的计算量随着观测值的增加也会随之增加。因此,扩展形式的Sigma点滤波方法也得到了广泛的应用。文献[24]设计了Sigma点卡尔曼滤波的平方根。该方法可以达到较高的估计精度,并且稳定性良好。由于滤波器的平方根具有保证协方差矩阵非负的优点,因此文献[25]在SLAM问题中设计了平方根无迹卡尔曼滤波,改善了算法的应用效果。同时,文献[25]改进了文献[26]的成果,设计了一种迭代平方根的UKF-SLAM,文献[27]设计了AUKF-SLAM。
根据现有的研究,四元数的应用具有多方面的优点,主要体现在计算量小,精度高,非奇异性和可全姿态工作等方面。部分学者基于四元数进行了研究,其中文献[28]针对UKF计算量较大的问题,提出一种经过改进的四元数无迹卡尔曼滤波算法。通过四元数UKF中四元数和修正罗德里格斯参数之间的线性变换,避免了频繁切换四元数和误差罗德里格斯参数所可能带来的计算错误和测试量增大的现象。文献[29]提出一种基于模糊逻辑四元数的平方根UKF姿态估计算法。采用模糊逻辑的平方根协方差形式作为更新参数,既降低了算法的计算量和复杂度,又保证了数值的稳定性。文献[30]提出一种用于磁角速率和重力传感器的线性卡尔曼滤波器,该滤波器处理角速率、加速度和磁场数据,以获得四元数表示中的方向估计。该算法将四元数方向计算为两个代数四元数的组合。两个四元数的解耦性质使方向的滚转和俯仰分量不受磁干扰的影响。文献[31]基于UKF,提出一种四元数衍生无迹卡尔曼滤波的无人机姿态估计方法,该方法实时性及精度方面都强于无迹卡尔曼滤波。文献[32]提出一种四元数状态切换无迹卡尔曼滤波方法。通过罗德里格斯参数与四元数结合的无迹卡尔曼滤波,利用时间更新和量测更新的过程中切换滤波状态来减少计算量,以此增加系统的实时性、精度和稳定性。
本文旨在解决移动机器人运动过程中的非线性位姿估计问题。首先列出了扩展卡尔曼滤波和无迹卡尔曼滤波SLAM的推导方程。根据无迹卡尔曼滤波涉及高阶矩阵运算导致时间计算增加的现状,在无迹卡尔曼滤波的基础上增加了平方根滤波。同时,利用四元数全姿态操作,准确性高的特点,通过乘性误差四元数对平均点和四元数点之间的距离进行描述,并降低滤波状态的维数,减少计算耗时。
1 扩展卡尔曼滤波和无迹卡尔曼滤波
1.1 移动机器人SLAM的线性化
针对移动机器人SLAM的研究比较多,该问题可以描述为机器人从处于特定环境中的某位置开始运动,实时对附近环境信息进行探测和感知,并以增量方式形成地图。对于SLAM问题,在时间k处定义以下状态向量。
xr,k:描述机器人姿态的状态向量。
uk:机器人从k-1至k时刻的控制矢量。
xfi:描述特征在时间i中位置的向量,且特征的真实位置不随时间变化。
zk:机器人当前位置到特征的观测向量。
SLAM过程可以由运动方程和观测方程来描述。假设在t=0至t=N的时间内,有位姿x0至xN,并且有路标y1,y2,…,yM。运动和观测方程为
xk=f(xk-1,uk)+wkk=1,2,…,N
(1)
zk,j=h(yj,xk)+vk,jj=1,2,…,M
(2)
由于x、y均属于需要估计的变量,因此可以将二者认为是满足特定概率分布的随机变量。已知xk代表k时的全部未知量,对应的全部观测表示为zk
(xk=f(xk-1,uk)+wkk=1,2,…,N
(3)
zk=h(xk)+vk)
(4)
现在考虑第k时刻的情况。用过去0到k中的数据,来估计现在的状态分布:那么SLAM问题可以用式(1)描述为
P(xr,k|z1:k,u1:k)
(5)
估计后验概率密度分布P(xk|zk,uk)具体划分为两个不同的过程,分别是预测、更新,具体的过程如下所示。
(1) 预测阶段:根据机器人的运动模型和当前位置,预测机器人下一时刻的状态。
机器人系统的先验概率密度为
zk-1,uk-1)dxk-1
(6)
(2) 更新阶段:在计算出观测模型和先验概率密度后,利用传感器所获取到的信息更新系统内的状态估计量。因此,系统的后验概率密度为
(7)
P(zk|xk)是观测模型。根据马尔可夫假设,当前状态已知时,前一次观测和当前观测是相互独立的,因此P(zk|zk-1,uk)是归一化常数。
如果运动模型和观测模型满足线性分布,则可采用卡尔曼滤波算法求解。当不满足时,积分计算很难实现,可采用扩展卡尔曼滤波进行求解。
1.2 扩展卡尔曼滤波

非线性离散系统的模型为
xk=f(xk-1)+wk-1
(8)
zk=h(xk)+vk
(9)
式中,wk和vk分别受到高斯白噪声的影响。

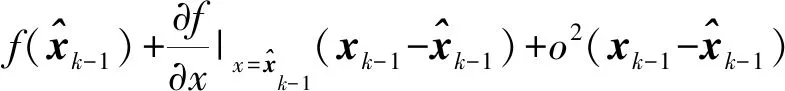
(10)
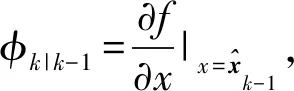
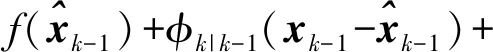
(11)
忽略高阶项的影响,式(7)可以简化为
(12)
利用状态转移函数,状态的单步预测值为
(13)
因此,对应的误差方差形式为
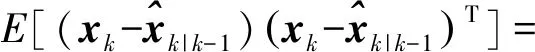
φk|k-1Pk|k-1Qk|k-1+Qk
(14)


(15)
从测量函数获得的测量向量的单步预测值为
(16)
因此,对应的预测误差方差矩阵为
(17)
状态增强矩阵为
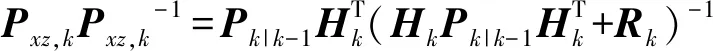
(18)
因此,时间k的估计状态向量为
(19)
状态误差协方差矩阵更新为
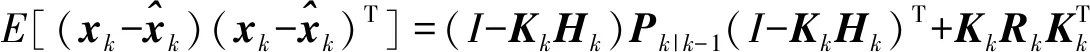
(20)
1.3 无迹卡尔曼滤波
传统的EKF存在着两个难以克服的问题:一是EKF算法的一阶泰勒展开忽略了非线性函数高阶导的影响,当非线性度较强时,则容易降低滤波精度,特别是不低于二阶的截断误差会产生更显著的影响;二是有的非线性函数并没有雅可比矩阵,这也让EKF算法在某些条件下不可用。近来出现的无迹卡尔曼滤波方法在应用中显示出一定的优势。该算法根据系统状态的先验均值和方差选择一组统计特征与之前的统计特征状态一致的确定性Sigma采样点。再通过线性传递函数得到一组新的Sigma点,在此基础上可以得到采样点的统计特征,即为对应的后验统计分布。从本质上来看,该方法实际上逼近的是非线性函数的概率密度分布,所以无须对雅克比矩阵进行计算,以此可以实现对非线性函数的处理,相对于传统的扩展卡尔曼滤波方法具备了明显的优势。
UKF采用递推估计的方式,求得状态量的最优方差估计值,避免了由高阶项截断而产生的系统截断误差,相较于EKF,提高了系统的解算精度。
对于无迹变换而言,需要确保在达到采样均值x以及协方差P的基础上选取合适的Sigma点,Sigma点数量取决于所选的采样策略。目前较为常见的采样策略是2n+1 Sigma点对称采样。采样完成之后基于非线性变换方式对Sigma点进行处理,可以得到对应的均值与协方差,然后将其应用到各个Sigma点中,采用相同的处理方式可以得到新的Sigma点。该方法相对于扩展卡尔曼滤波可以得到更多的观测假设。UT变换的应用体现出明显的优势,降低了截断误差对于数据融合所造成的影响,无须进行线性化处理的过程,可以达到更高的求解精度。因此,状态统计特性的估计比EKF算法更准确。
Sigma点的选择和比例可根据以下公式选择
λ=α2(n+χ)-n
(21)
Sigma点序列为
(22)
协方差的权重和Sigma点序列的估计计算为
(23)
式中,α代表与Sigma点扩散尺度有关的参数;β≥0;x服从高斯分布;n代表状态向量维度。
在非线性系统中引入UT变换,可以得到无迹卡尔曼滤波,具体的过程如下。
(1) 初始化
(24)
(25)
(2) 时间更新。时间更新中Sigma点和权重的选择为
(26)
(27)
(28)
利用非线性测量函数计算k时刻系统状态、均值和协方差的单步预测χk|k-1(i)=f(χk-1(i)),
(29)

(30)
(3) 测量更新。测量更新中Sigma点和权重的选择为
(31)
(32)
(33)
利用非线性测量函数计算k时刻系统状态单步预测、均值和方差以及互协方差Zk|k-1(i)=h(ξk|k-1(i)),有
(34)

Zk|k-1(i))T]+Rk
(35)
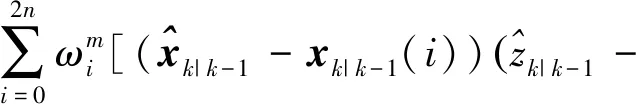
Zk|k-1(i))T]+Rk
(36)
(4) 状态增益。状态增强矩阵、估计值和状态误差方差值为
(37)
(38)
(39)
无迹卡尔曼滤波相对于扩展卡尔曼滤波在精度上具有一定的优势,并且计算难度较小,无须计算雅克比矩阵,所以可以应用到更多的场景中。
2 平方根无迹卡尔曼滤波
Sigma点的确定性采样与协方差P的平方根运算有关,如果是高阶矩阵则极易影响到计算的效率。其次,在运算过程中,受到数值舍入误差的影响导致计算稳定性降低。因此,文献[34]在研究过程中设计了基于平方根的UKF算法。该方法在平方根计算过程中采用了Cholesky分解等方式,具体的内容如下。
(1) 初始化
(40)
(41)
式中,chol{}表示矩阵的Cholesky分解。
(2) 时间更新。时间更新中Sigma点和权重的选择为
(42)
(43)
(44)
利用非线性测量函数计算k时刻系统状态、均值和互协方差的单步预测Zk|k-1(i)=h(ξk|k-1(i)),有
(45)
(46)
(47)
式中,qr{…}代表奇异值分解的过程;cholupdate{…}代表矩阵更新的过程。
(3) 测量更新。测量更新中Sigma点和权重的选择为
(48)
(49)
(50)
利用非线性测量函数计算k时刻系统状态、均值和互协方差的单步预测Zk|k-1(i)=h(ξk|k-1(i))。
(51)
(52)
(53)
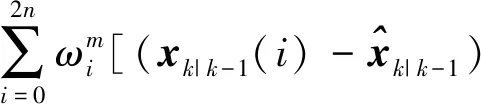
(54)
(4) 状态增益。状态增强矩阵、估计值和状态误差方差值为
(55)
(56)
Uk=KkSzz,k
(57)
(58)
3 四元数平方根无迹卡尔曼滤波
传统的非线性优化方法在求解移动机器人的位姿估计时,往往面临计算量大的问题,需要花费较多的时间才能够完成计算。四元数则能够有效地解决上述问题,其优势在于降低了计算量,提升了计算的精度,并且可以达到全姿态工作的目标,所以广泛应用到了姿态表示中[35]。国外部分学者很早开始在此领域进行了研究,在19世纪,W.R.Hamilton提出了四元数,但是受到技术以及硬件条件等因素的影响并未引起广泛的关注,也没有得到较多的应用。后来随着在此领域研究的深入,以及计算机性能的不断提升,对于四元数的研究和应用逐步增多,可以充分发挥其应用的优势与特色。另外,其相对于欧拉角更为简单,大幅度降低了计算的复杂度。正是由于具备了上述优势,使得四元数在扩展卡尔曼滤波中有着广泛的应用。文献[36]提出了一种基于四元数的二阶EKF算法,计算了Taylor展开的二阶精度,提高了姿态估计的精度,但计算量也有所增加。文献[37]提出了一种基于修正Rodriguez参数和姿态四元数转换的无迹Kalman滤波算法。该算法通过参数间的相互转换有效地提高了姿态估计的精度,但这种相互转换无疑增加了算法的复杂度。
本文提出一种四元数平方根无迹卡尔曼滤波(Quaternion Squareroot-UKF,QSR-UKF)算法。算法将四元数均值问题转化为拉格朗日代价函数的极值问题,无须姿态参数切换,矢量部分属于姿态变量,标量则通过单位四元数计算。这种计算方式解决了四元数Sigma点在选取过程中的可能出现的干扰问题,降低了平方根无迹卡尔曼滤波状态的维数。
在算法中利用了乘性误差四元数,其可以对平均点和四元数点之间的距离进行描述,有助于解决奇异值分解的计算量大和特征向量法烦琐的计算步骤等问题。除了上述优势之外,同样有效地解决了四元数加权均值问题,可以保持清晰的计算流程,并得到精度较高的结果。
在UKF算法中加入四元数形成Q-UKF算法,同样存在一定的不足,包括误差协方差矩阵的对称性等。本文中针对上述问题进行了分析和设计,在此基础上设计了一种新的四元数平方根UKF(QSR-UKF)算法。
选定的状态变量x=[ρT,βT]T,其中ρ是姿态四元数的矢量部分;β是陀螺漂移。
(1) 初始化
(59)
(60)
(2) 时间更新。Sigma点避免了状态误差方差矩阵的平方根运算
(61)
状态Sigma点分为姿态部分和陀螺漂移部分
(62)
考虑到过滤器更新过程中经过四元数,因此这里选择Sigma点作为四元数点
(63)
(64)
(65)
选择陀螺漂移Sigma点作为
(66)
(67)
(68)
时间更新主要划分为两部分,分别是四元数、非四元数,前者的具体表达式为
(69)
由于陀螺仪漂移是一个线性传递过程,其时间被更新为
(70)
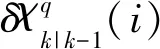
(71)
(72)
(73)
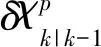
对于漂移部分,状态预测均值以及协方差依次为
(74)
(75)
(76)
(3) 测量更新。与时间更新的Sigma点选择类似,测量更新的Sigma点为
(77)
分为四元数和陀螺漂移,具体为
(78)
测量更新中四元数的Sigma部分为
(79)
(80)
(81)
选择测量更新中的陀螺漂移部分Sigma作为
(82)
(83)
(84)
四元数测量更新为
(85)
则四元数测量误差协方差矩阵和状态测量误差方差矩阵为
(86)
(87)
(4) 状态增益。由上可知,状态增益矩阵为
(88)
由上可知,状态增强矩阵为
(89)
因此,四元数状态更新量和陀螺仪漂移更新为
(90)
(91)
状态误差方差矩阵为
Uk=KkSzz,k
(92)
(93)
4 仿真试验
本文分别在公寓环境下以及迷宫环境下对移动机器人SLAM进行了测试,分别对EKF、SR-UKF和QSR-UKF进行了仿真。所有仿真试验均在Ubuntu 18.04中使用ROS Melodic进行,在英特尔Core i7-8750HCPU上运行。在本次研究中已经事先确定了地图特征和观测特征之间的关系,由此降低了数据关联错误所产生的不利影响。然后针对3种算法的应用效果进行了对比分析,通过指标量化分析,包括运行时间和精度,继而可以得到客观的结果。
本文创建两个试验环境,公寓环境大小为15 m×15 m,迷宫环境大小为80 m×8 0m,共有18个导航标记和28个静止点的特征以及一些随机设置的点特征。如图1和图6所示,移动机器人的初始位置为(0,0)移动速度为v=3 m/s。另外,激光雷达采样时长为0.2 s,探测距离最大值是30 m,距离误差为0.1 m,过程噪声协方差矩阵Q为[1.900;01.20;0000.8],观测噪声协方差矩阵R为[0.50;000.1]。
针对仿真中的干扰因素进行设计,在100个控制周期中任意设置外部干扰,具体为3—5次。通过这种方式可以对SLAM精度产生一定的影响。在本次试验中,采用了3种算法来对移动路标进行估计,分别是EKF-SLAM,SR-UKF-SLAM、QSR-UKF-SLAM算法。在各个参数设置完成之后可以进行仿真的过程,具体得到的结果如图2—图5、图7—图10所示,其中“+”“·”分别代表环境特征的真实以及估计的位置;而实际移动路线和估计路线分别为如图1—图5所示。
4.1 准确度
根据3种方法得到的姿态误差信息即为图2—图4及图7—图9中所示,而对应的环境位置信息如图5及图10中所示。根据图中所示的信息可知,相对于EKF-SLAM,其他两种算法可以达到更高的精度要求。通过调整协方差矩阵和增加噪声误差,可以看出SR-UKF和QSR-UKF-SLAM具有更高的姿态估计精度。根据本文研究的结果可知,受到噪声因素的影响,导致EKF容易发散,增大了EKF-SLAM控制的难度,而这种现象与噪声的类型有关,如果不是零均值白噪声即容易出现发散的问题。SR-UKF-SLAM则可以实现噪声适应,主要与无迹变换等处理过程有关。虽然3种算法与机器人真实的路径都存在一定的误差,但是QSR-UKFSLAM算法机器人轨迹估计和路标估计的误差都小于EKF-SLAM和SR-UKF-SLAM算法,所以QSR-UKFSLAM算法的位姿估计精度最高。
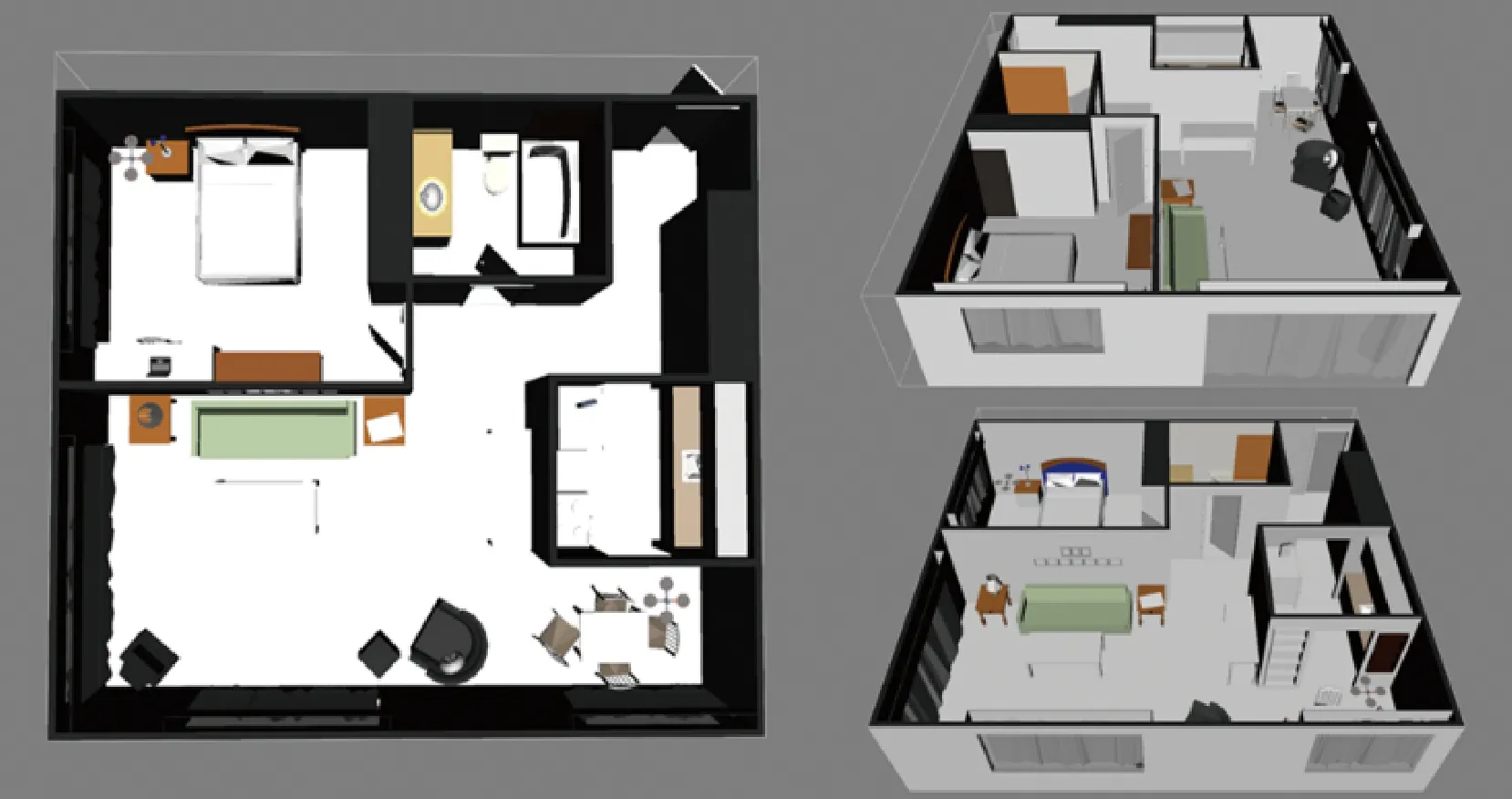
图1 公寓仿真环境Fig.1 Simulation in apartment environment
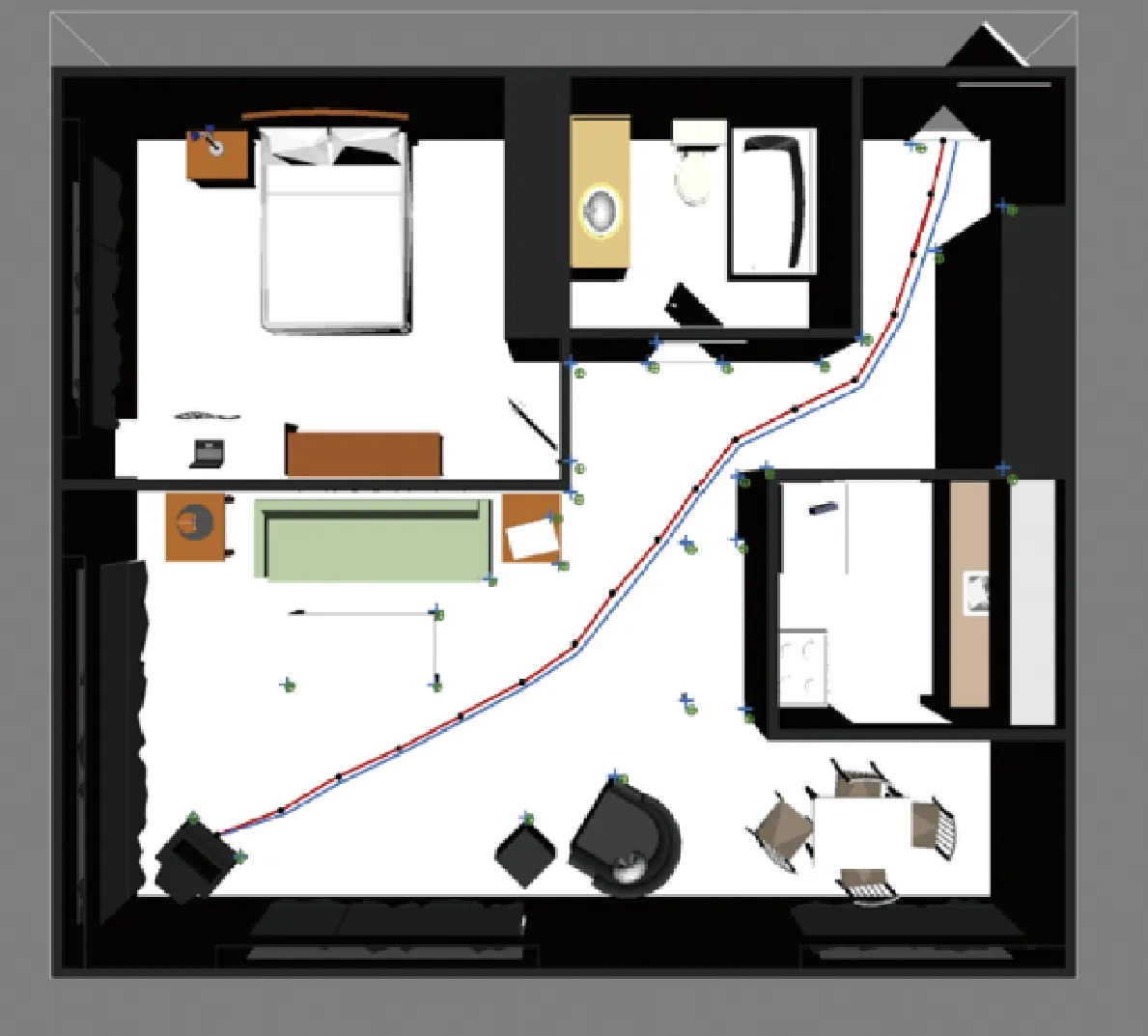
图2 扩展卡尔曼滤波在公寓内的仿真结果Fig.2 Estimate result of EKF in apartment environmen
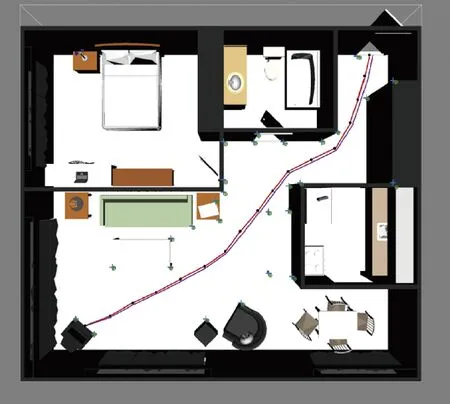
图3 平方根无迹卡尔曼滤波在公寓内的仿真结果 Fig.3 Estimate result of SR-UKF in apartment environment

图4 四元数平方根无迹卡尔曼滤波在公寓内的仿真结果 Fig.4 Estimate result of QSR-UKF in apartment environment
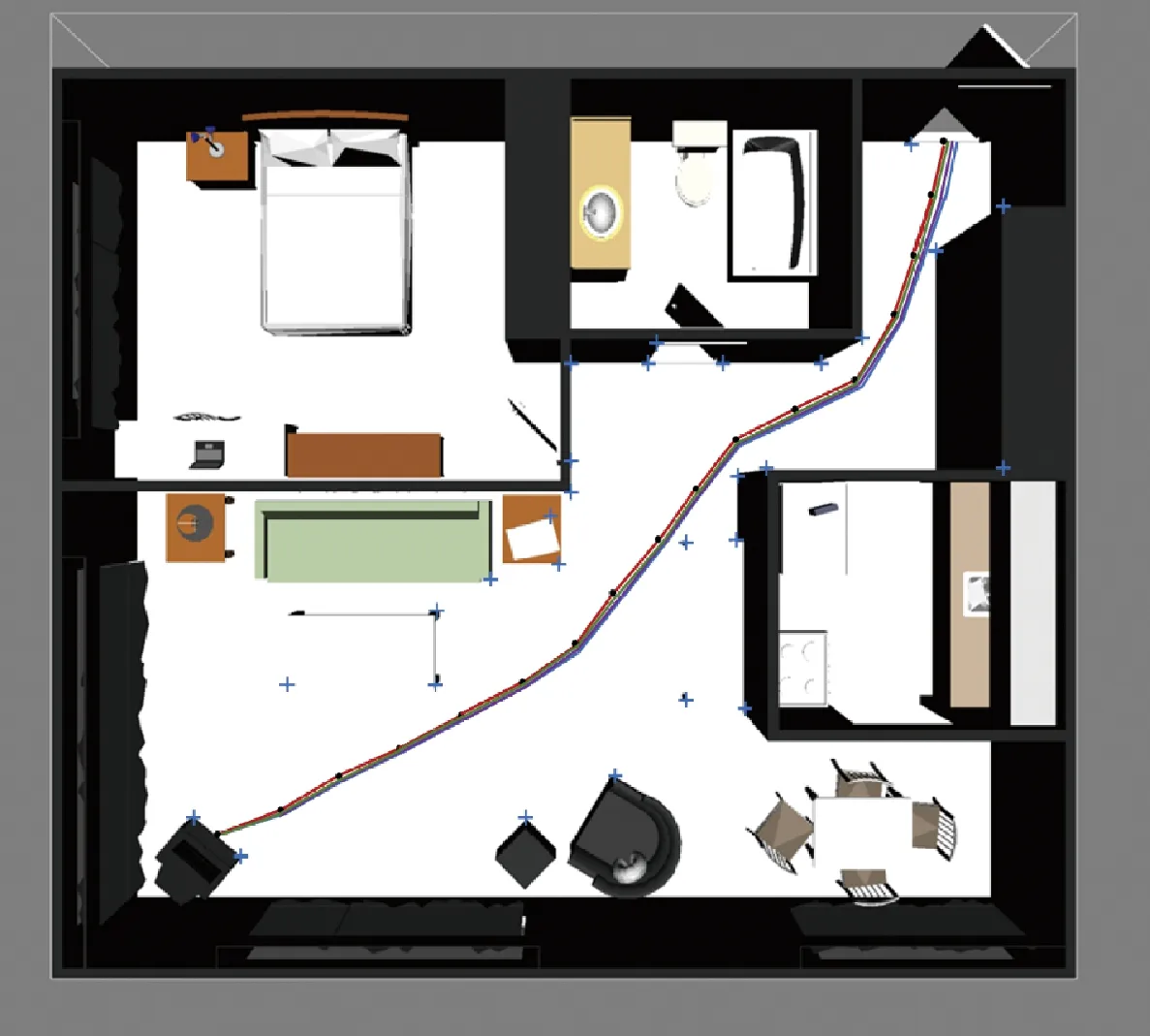
图5 3种在公寓内的仿真结果的比较Fig.5 Estimate result of three algorithms in apartment environment

图6 迷宫仿真环境Fig.6 Simulation in maze environment
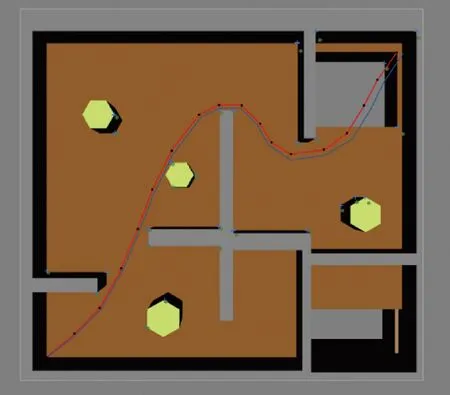
图7 扩展卡尔曼滤波在迷宫内的仿真结果Fig.7 Estimate result of EKF in maze environment
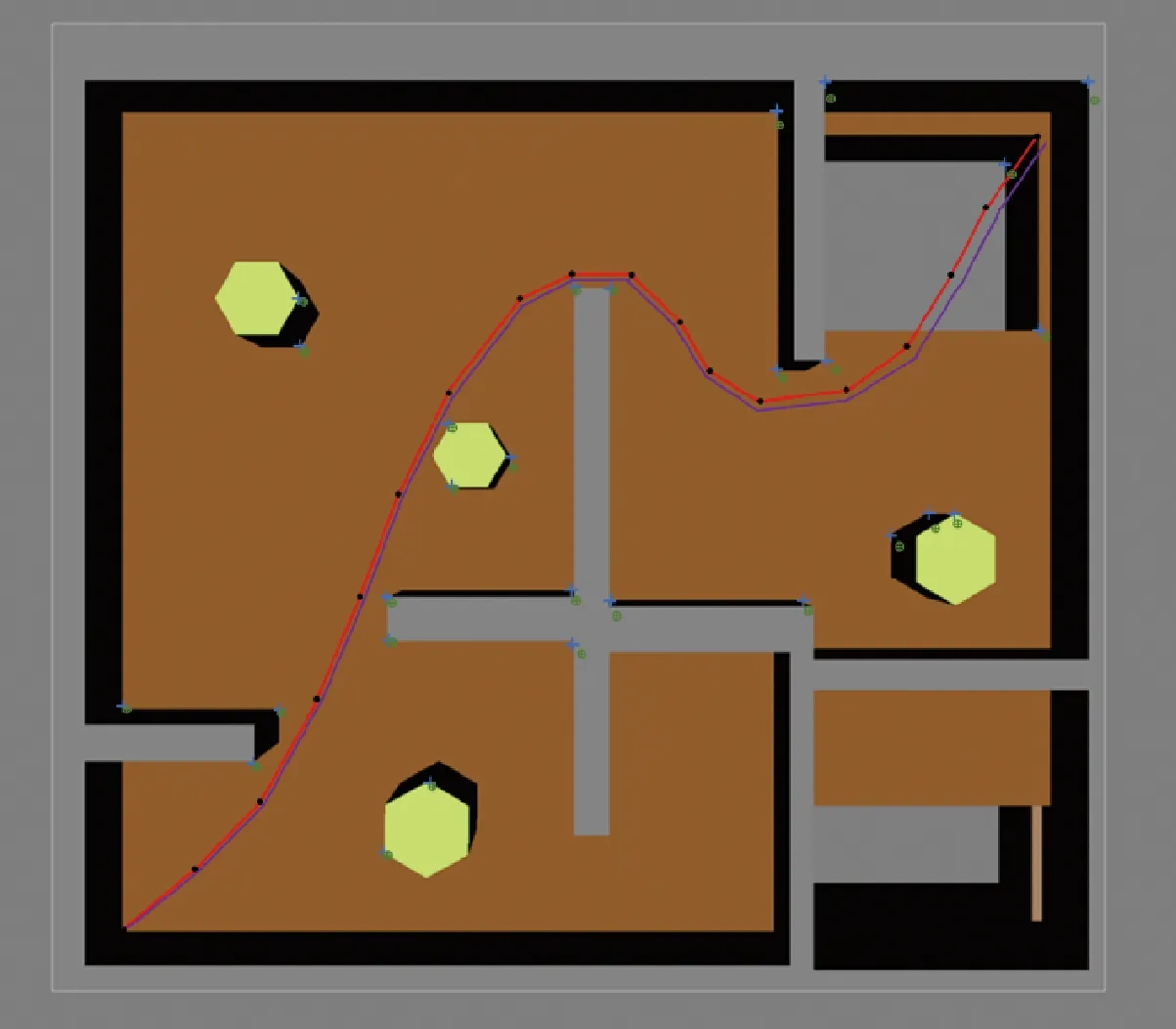
图8 平方根无迹卡尔曼滤波在迷宫内的仿真结果Fig.8 Estimate result of SRUKF in maze environment
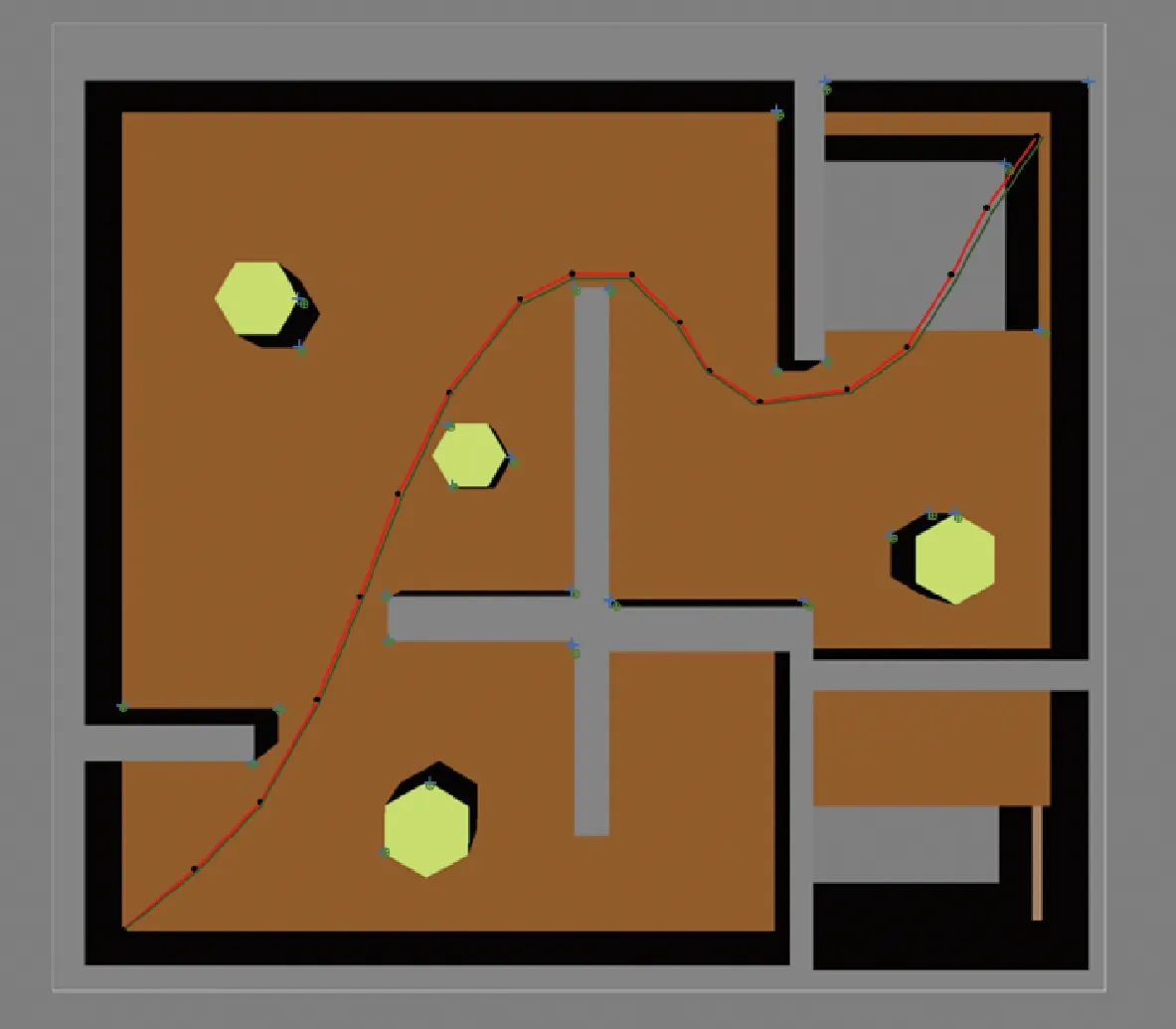
图9 四元数平方根无迹卡尔曼滤波在迷宫内的仿真结果Fig.9 Estimate result of QSR-UKF in maze environment

图10 3种在公寓内的仿真结果的比较 Fig.10 Estimate result of three algorithms in maze environment
为了更详细地比较3种算法在不同的运动噪声和观测噪声下的姿态估计精度,在研究过程中通过RMSE来进行评价,针对3种算法的姿态估计精度进行了对比分析,为了提升仿真结果的准确性与可靠性,将仿真次数设置为20次,最终得到的信息见表1。表1主要包括两个指标,分别是RMSE_P、RMSE_L,二者分别对应着机器人、路标位置估计。
根据表1和表2的信息可以明显地看到,在公寓环境中,QSR-UKF-SLAM算法在机器人位置估计和路标估计上的RMSE比EKF-SLAM分别降低了55.20%、47.29%,比SQ-UKF-SLAM算法在轨迹和路标估计的RMSE分别下降了32.81%、31.57%。在迷宫环境中,QSR-UKF-SLAM算法在机器人位置估计和路标估计上的RMSE比EKF-SLAM分别降低了64.78%、67.92%,比SQ-UKF-SLAM算法在轨迹和路标估计的RMSE分别下降了20.08%、29.53%。3种算法在路标位置的均方根误差曲线如图11和图12所示,结合图中所示的信息可知,基于SR-UKF、QSR-UKF的SLAM算法可以达到较高的位姿估计精度,估计误差最低的是QSR-UKFSLAM算法,由此验证了算法的应用效果。

表1 3种算法在公寓环境中移动机器人位置估计以及路标位置估计的均方根误差Tab.1 RMSE of three algorithms in robot position estimation and landmark position estimation in maze environment
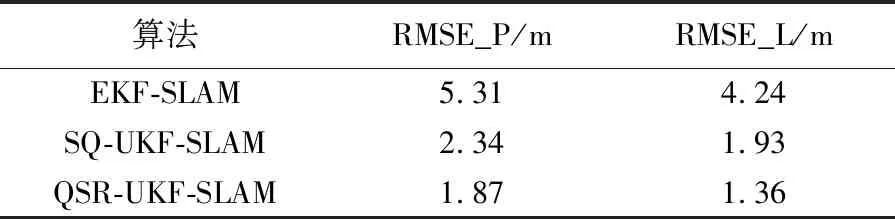
表2 3种算法在迷宫环境中移动机器人位置估计以及路标位置估计的均方根误差Tab.2 RMSE of three algorithms in robot position estimation and landmark position estimation in maze environment

图11 在公寓环境中3种算法在路标位置上的均方根误差Fig.11 RMSE curve of three algorithms in landmark position

图12 在迷宫环境中3种算法在路标位置上的均方根误差曲线图Fig.12 RMSE curve of three algorithms in landmark position
表3显示了在迷宫环境下,EKF、SR-UKF、QSR-UKF-SLAM 3种算法在相同条件下的X、Y以及姿态角方向的绝对误差平均值以及方差的比较。同时从表中可以看出,SR-UKF-SLAM和QSR-UKF-SLAM计算精度在整体上要比EKF-SLAM高;SR-UKF-SLAM和QSR-UKF-SLAM计算精度相对比较接近,因此,SR-UKF-SLAM和QSR-UKF-SLAM能有效降低EKF所带来的线性化误差。总体而言,QSR-UKF提高了机器人运动过程的稳定性,具体性能优于EKF-SLAM和SR-UKF-SLAM。本文未比较在公寓环境下3种算法在X、Y以及姿态角方向的绝对误差平均值以及方差。原因是公寓环境较小,X、Y以及姿态角方向的绝对误差平均值以及方差都较小,可比性不足。

表3 EKF、SR-UKF、QSR-UKF-SLAM在X、Y和姿态角上的绝对误差均值以及误差方差Tab.3 Absolute error mean and error variance of EKF, SR-UKF and QSR-UKF-SLAM in X, Y and attitude angles
4.2 运算时间
基于QSR-UKF-SLAM与EKF-SLAM、SQ-UKF-SLAM算法在公寓以及迷宫环境下的运行时间见表4及表5,结合表中的信息可知,总运行时间最低的是基于QSR-UKF的SLAM算法。并且,QSR-UKF-SLAM算法在单步运行时间上也少于其他两种算法。

表4 基于QSR-UKF-SLAM与EKF-SLAM、SQ-UKF-SLAM算法在公寓环境下的运行时间Tab.4 Running time of QSR-UKF-SLAM, EKF-SLAM and SQ-UKF-SLAM in apartment environment
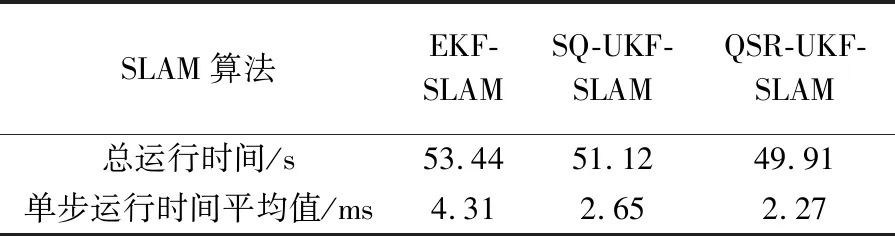
表5 基于QSR-UKF-SLAM与EKF-SLAM、SQ-UKF-SLAM算法在迷宫环境下的运行时间Tab.5 Running time of QSR-UKF-SLAM, EKF-SLAM and SQ-UKF-SLAM in maze environment
5 结 论
本文对移动机器人SLAM算法的位姿估计与校正问题进行了研究,针对基于非线性优化的扩展卡尔曼滤波和无迹卡尔曼滤波位姿优化算法的局限性,给出了相应的解决方案。本文在无迹卡尔曼滤波中加入Sigma点的平方根以提高其稳定性和估计精度。其次,根据四元数具有计算量小、精度高的优点,将其向量当作姿态变量,解决了四元数Sigma在选取过程中的可能出现的干扰问题。并且相较于无迹卡尔曼滤波降低了滤波状态的维数,减少了计算耗时。综上,本文提出了四元数平方根UKFSLAM位姿估计算法。仿真试验结果表明,与EKF和SR-UKF算法相比,QSR-UKF算法采用了相对简单的奇异值分解和Cholesky分解来实现误差方差矩阵的平方根运算,使得算法的数值运算特性得到了一定程度的改善,同时也提高了算法的稳定性。

