无证书线性同态聚合签名方案研究

茅 磊

（江苏建筑职业技术学院信电工程学院，江苏徐州 221116）

0 引言

随着计算机和互联网技术的不断发展，大数据、云计算、物联网、人工智能等新兴技术步入人们生活。云存储是云计算在概念上的延伸与发展。云存储是通过集群应用、网络技术和分布式文件系统，将网络中大量不同类型的存储设备通过软件集合到一起，共同对外提供数据存储和业务访问功能的一个系统。目前，云存储已逐步实现商业化，走进了人们的日常生活中，国内已涌现出一批云存储服务提供商，如百度云、阿里云等。越来越多的企事业单位也习惯将数据搬至云端存储，实现数据外包，不仅可以节约自身存储空间，降低数据维护管理代价，还可以在任何时间、任何地点通过任何可接入互联网的设备高效便捷地访问云端数据。随着云存储的不断商业化，云中数据完整性的保护越来越受到用户关注。基于此，本文采用密码学中的数字签名技术，设计出一种适用于云存储的高效安全文件完整性审计方案。

1 相关研究

数字签名是公钥密码学的重要研究方向，其可对被签名文件数据提供真实性、完整性以及不可否认性的技术服务。随着研究的不断深入，许多适用于不同使用环境的特殊数字签名，如同态签名、聚合签名、无证书体制下的数字签名等应运而生。这些数字签名既有普通签名的功能，也有自身独有的特点，若将其有机组合并加以灵活使用，在云存储环境中可起到事半功倍的效果。

1.1 同态签名

同态签名由Johnson 等提出。设数字签名的消息空间

M

和签名空间∑上的二元运算符分别为⊕和⊗，有两个来自

M

和∑上的消息签名对(

m

,

σ

)和(

m

,

σ

)，其中

σ

=

f

(

m

)，

σ

=

f

(

m

)，若签名算法

f

是代数系统（

M

，⊕）到（∑，⊗）上的同态映射，则有

f

(

m

⊕

m

)=

f

(

m

)⊗

f

(

m

)=

σ

⊗

σ

成立。从这一点不难看出，同态签名在一定程度上放宽了数字签名的安全性。一般数字签名方案在安全性上要求达到在适应性选择消息下的存在性不可伪造，而同态签名则要求在同一数据集中，各消息的签名可以由其他已知的消息签名导出，不必再使用复杂的签名算法生成。但在该数据集外，即在不同数据集中的消息签名不能由其他数据集中的消息签名导出，只能由数字签名算法生成。根据目前密码学界的观点，上述同态签名可以分为线性同态签名、多项式同态签名以及全同态签名3 类，以线性同态签名使用最多最广。线性同态签名是针对一个线性子空间基中的各个向量进行签名，是一种高效快捷的轻量级同态签名方案。例如，Wu 等使用无证书线性同态签名设计了一种抵抗网络编码污染的签名方案，并探讨了该方案在物联网上的应用；Lin 等研究了标准模型下基于格的线性同态签名方案，该方案具有较短的公钥。同态签名在云存储中也可发挥重要作用。云存储环境中生成的数据文件往往是动态增长的，如果采用普通数字签名保证动态增长数据的完整性并实现数据的可公开验证效果必然不理想。如图1 所示，假设用户

A

租用云服务器存储自身每天产生的数据，第1 天用户

A

产生数据块

m

，第2 天产生的数据块记为

m

，以此类推。如果采用一般的数字签名保障数据的可公开验证，该用户需每天对产生的数据进行签名，并将数据和签名均存储在云服务器上。而在验证数据完整性时，又要从云服务器上依次下载这些数据及其对应的签名。若需验证3个数据块的完整性，则要分别下载3个数据块和3个签名，并进行3 次验证运算。采用同态签名时，每产生一部分新数据就要使用签名算法产生对应的签名并将其存储在云端，而验证时又要下载所有数据块及其对应的签名，还要进行与数据块相同数量级的验证运算，势必会在用户端产生大量验证运算，消耗更多云存储空间，而且下载数据和签名时也会占用更多网络带宽。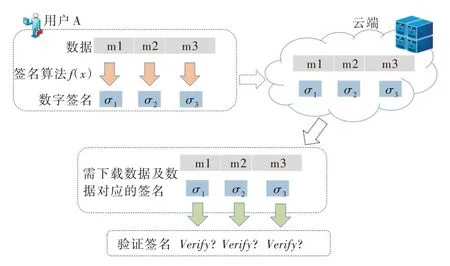

Fig.1 Using ordinary digital signature to verify data integrity图1 使用普通数字签名验证数据完整性

1.2 聚合签名

聚合签名概念由Boneh 等于2003 年提出，旨在提高验证大量单个签名的效率。使用普通数字签名方案进行签名合法性验证时，需要对每个签名逐个验证，在云存储中进行数据审计时使用该种方案的繁琐程度和运算存储代价难以承受。如果采用聚合签名，则可将来自不同用户的数字签名压缩成一个签名，验证聚合后的签名等同于验证所有聚合前单个用户的签名。使用聚合签名不仅可以保证云存储中数据的完整性，还可实现在云端数据审计工作的公开批量验证。随着对聚合签名研究的深入，Zhang 等发现了来自聚合签名者内部的合谋攻击，并在此基础上提出新的聚合签名安全模型，认为当且仅当每个被聚合的单个签名是合法签名时，最后的聚合签名才是合法的；曹素珍等提出无证书高效聚合签名方案，虽然效率较高，但仍不能抵抗合谋攻击；吴戈设计了能抵抗合谋攻击的基于身份与无证书的聚合签名。

1.3 无证书密码体制

无证书密码体制是Al-Riyami 等针对身份密码体制的不足所提出的改进方案。基于身份的密码体制往往需要假定密钥生成中心完全可信，这是由于用户密钥完全掌握在密钥生成中心（KGC）手中。但在云存储中通常认为云服务器是不可靠的，云服务商存在有意无意损害用户存储在云端数据的行为（如不可抗的自然灾害、云服务器本身的物理损害、黑客攻击等）。如果使用基于身份的数字签名，当用户数据发生损坏时，云服务商可能会使用身份系统中的用户完整私钥逃避责任，这是由于云服务商掌握用户的签名私钥，当发生数据损坏时，“不诚实”的云存储服务商可能会使用用户签名私钥对损坏后的数据重新签名，而用户却全然不知。无证书密码系统不仅可以方便地搭建在云存储服务系统中，还能克服身份密码系统中密钥管理中心权利过于集中的缺点。

2 方案设计思路

上述3 种密码学技术各有所长：无证书密码体制可以保障用户签名私钥的安全，抵抗不诚实的KGC；同态签名可以压缩同一数据集内部动态增长的各数据签名；聚合签名可以将不同数据集中的数字签名进一步压缩。因此，本文结合以上3 种技术设计出一种适用于云存储中数据审计的无证书线性同态聚合签名。

如图1 所示，首先将无证书密码体制搭建在云存储系统上，由云服务商生成无证书密码系统的相关参数，并产生用户签名时的部分私钥。将私钥通过安全信道传送给用户，用户自己生成并掌握签名的秘密值。用户的签名完整私钥由部分私钥和秘密值组成，除用户以外，没有任何人再能掌握完整的签名私钥。因此，将无证书密码体制部署在云存储系统中可避免云服务商逃避责任。

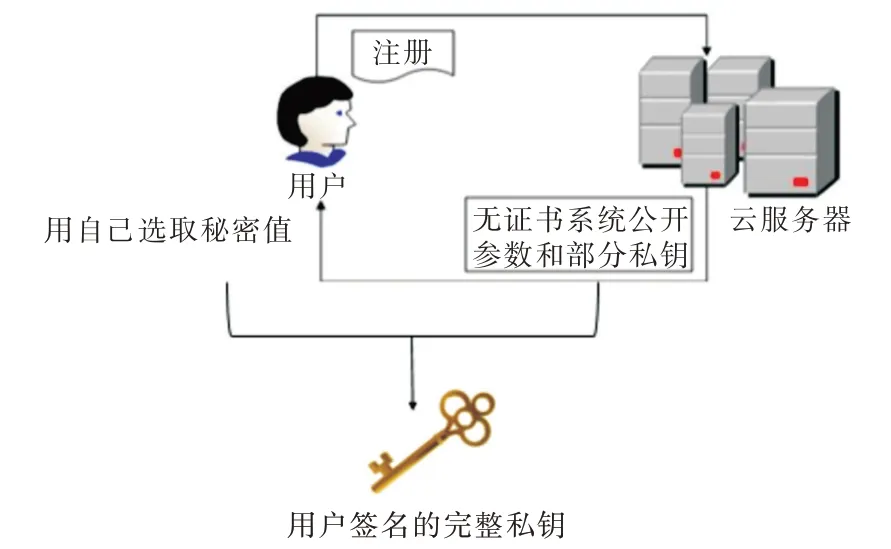
Fig.2 Deploying certificateless system on cloud server图2 在云服务器上部署无证书系统

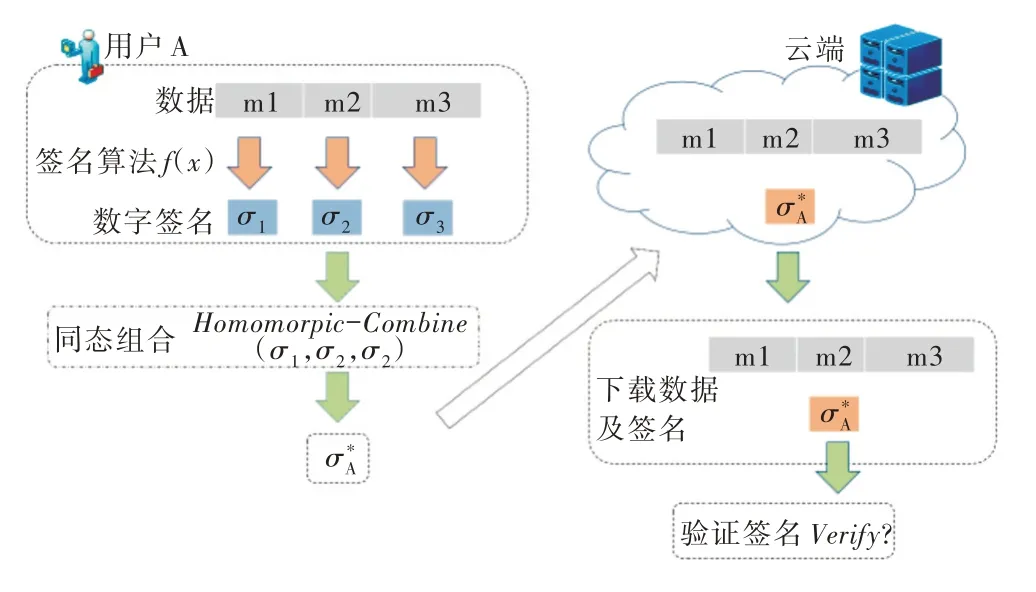
Fig.3 Using homomorphic signature to verify data integrity图3 使用同态签名验证数据完整性

最后，基于聚合签名的特点，将来自不同数据集的同态签名进一步聚合压缩。将同态签名与聚合签名结合起来形成同态聚合签名，可解决在云存储中多方数据公开批验证的问题。如图4 所示，假设需要验证N个用户数据，只需使用聚合签名算法

Aggregate

将这N个用户数据生成的同态组合签名聚合成一个签名然后验证一次即可。因此，使用无证书线性同态聚合签名可以在保障云存储中数据块完整的前提下减少签名验证次数，提高审计效率。

Fig.4 Multi user data integrity verification using aggregate signature图4 使用聚合签名验证多用户数据完整性

3 无证书线性同态聚合签名的形式化定义

无证书线性同态聚合签名系统由以下9个概率多项式算法组成，分别为：

（1）

Setup

：密钥生成中心（KGC）输入为系统的安全参数1，产生系统的公开参数params 和系统主私钥msk。（2）

PartialPrivateKeyExtract

：输入用户身份ID，KGC 生成身份为ID 用户的部分私钥

D

。（3）

ProduceSecretValue

：用户运行生成秘密值

r

。（4）

ProducePublicKey

：用户运行生成公钥

PK

。

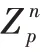
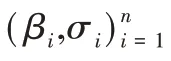
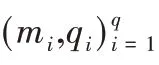
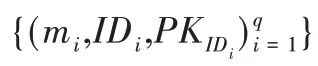
4 无证书线性同态聚合签名的安全模型

聚合签名的作用是将若干签名者生成的单个签名压缩成一个签名，因此只有当每个参与聚合的无证书线性同态签名合法时，生成的无证书同态聚合签名才合法。无证书同态聚合签名的特性可分为无证书同态签名方案的安全性和聚合算法的安全性两部分。

4.1 无证书同态签名的安全模型

对于无证书密码体制的安全模型而言，一般有两类攻击者：第一类攻击者可以替换系统的公钥，但不能访问主私钥；第二类攻击者则可以访问主私钥，但不能替换系统的公钥，通常又被称为“诚实而又好奇”的攻击者。同态签名的基本安全性要求为在适应性选择数据集下的存在性不可伪造，因此无证书同态签名方案在适应性选择身份、适应性选择数据集下存在性不可伪造的安全模型可以通过挑战者C 和攻击者（A或A）之间的游戏来刻画。

4.1.1 游戏1（第一类攻击者A）

（1）系统建立。挑战者C 获得系统的安全参数1后，生成公开参数

params

、系统主私钥

msk

、保密主私钥

msk

，将公开参数

params

发送给攻击者A。（2）询问。攻击者A可向挑战者C 进行创建用户询问（CU）、部分私钥提取询问（PPK）、秘密值询问（SVK）、公钥询问（PK）、替换用户公钥询问（PKR）、签名询问（Sign）。挑战者C 需要模拟随机预言器，给出上述方案中各算法的正确回答。在签名询问时，挑战者C 要模拟超级签名预言器，即攻击者A只提供用户身份

ID

和消息向量

m

，而不提供替换公钥后对应的秘密值，挑战者C 需要产生当前用户公钥（一般是被A替换后的公钥）下该数据集中消息向量

m

的合法签名

σ

，并发送给攻击者A。（3）伪造输出。攻击者A输出一个伪造（ID*，pk，τ*，m*，

σ

*），在以下情况成立时攻击者A在游戏中获胜：①

σ

*是在挑战身份ID*和对应公钥pk下，由τ*标记的数据集中消息m*的合法签名；②攻击者A没有询问过挑战身份ID*的部分私钥；③

τ

* ≠

τ

，即攻击者A没有询问过身份为ID*、公钥pk下由

τ

*标记的数据集m*上消息的签名。

4.1.2 游戏2（第二类攻击者A）

（1）系统建立。

C

获得系统的安全参数1后，生成公开参数

params

、系统主私钥

msk

、保密主私钥

msk

，将公开参数

params

发送给攻击者A。（2）询问。攻击者A可向挑战者C 进行创建用户询问（

CU

）、秘密值询问（

SVK

）、公钥询问（

PK

）、替换用户公钥询问（

PKR

）以及签名询问（

Sign

）。挑战者C 需要模拟随机预言器，给出上述方案中各算法的正确回答。在签名询问时，挑战者C 仍然要模拟超级签名预言器。（3）伪造输出。攻击者A输出一个伪造（ID*，pk，τ*，η*，

σ

*，f*），在以下情况成立时A赢得游戏2：①

σ

*是在挑战身份ID*和相应的公钥pk下，由τ*标记的数据集中消息m*的合法签名；②

τ

* ≠

τ

，即A没有询问过身份为ID*、公钥pk下由τ*标记的数据集m*上消息的签名；③A没有询问过挑战身份ID*对应的秘密值；④A没有替换过挑战身份对应的公钥。将攻击者在上述两个游戏中获胜的概率称为攻击者的优势。无证书同态签名方案在超级攻击者适应性选择身份、适应性选择数据集攻击下是存在性不可伪造（

EUFCLHS-ID-CDA

）的，任何概率多项式时间内的超级攻击者赢得两个游戏的优势是可以忽略的。

4.2 聚合算法的安全模型

张一名提出一种来源于聚合签名者内部的合谋攻击，其认为聚合签名安全模型中攻击者的能力有限，并在原基础上将攻击者的攻击目标修改为攻击者使用一系列单个签名伪造一个合法的聚合签名，在这些单个签名中包含至少一个非法签名。因此，聚合算法的安全模型可描述为：

（1）系统建立。挑战者获得安全参数后生成系统的各项参数

params

，以及验证聚合签名的公私钥对，然后将公钥

PK

和参数发送给攻击者。（2）询问阶段（

Query

）。询问阶段包括私钥询问（

SKRQ

）和聚合验证询问（

AVRQ

）两种。私钥询问为当攻击者进行私钥询问时，挑战者根据具体用户的ID 运行部分私钥提取算法和秘密值设置算法，将用户ID 的私钥返回给攻击者；聚合验证询问为当攻击者进行聚合验证询问时，挑战者通过运行聚合签名验证算法，回答攻击者所给的聚合签名是否合法。

（3）伪造输出。攻击者输出一个伪造（待聚合的消息，最后的聚合签名），如果满足以下条件，则认为攻击者在上述游戏中获胜：①攻击者输出的最后聚合签名是合法的；②在攻击者进行聚合的单个签名序列中，至少有一个签名是非法的。

从上述模型可以看出，攻击者在游戏中获胜实际上是使用一系列不完全合法的单个签名产生了一个合法的聚合签名。一个无证书同态聚合签名方案对于上述攻击者是安全的，在任何概率多项式时间内伪造最多

n

个用户聚合签名的超级攻击者在上述游戏中获胜的优势是可以忽略的。

5 无证书线性同态聚合签名方案

5.1 无证书同态聚合签名算法描述

（4）Produce-Public-Key：输入身份

ID

和秘密值

x

，产生用户的公钥

PK

=

g

。

式中，k=1，2，…，

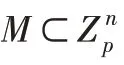
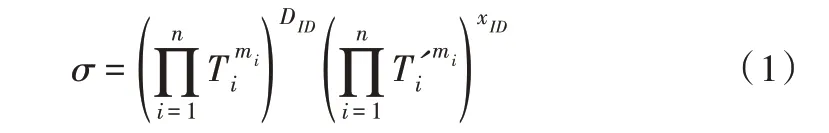
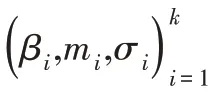
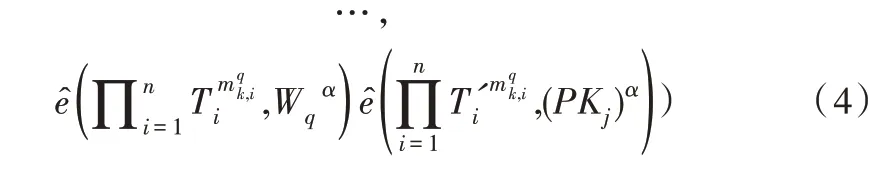
l

。如果

t

=

t

'，则该算法输出1，否则输出0。

5.2 无证书线性同态聚合签名的安全性

无证书线性同态聚合签名的安全性证明可分为两部分。

（1）本文省略无证书线性同态签名方案在适应性选择身份、适应性选择数据集中含有超级攻击者的证明方法，具体证明过程可参考文献［20］。

另一方面，

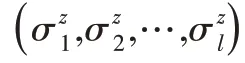
t

=

t

'成立，可得：

6 无证书线性同态聚合签名方案性能实验

在仿真实验过程中使用文献［20］的无证书线性同态签名方案（CLLHS）作为比较对象，对本文提出的无证书同态聚合签名方案的性能进行验证。对5 组实验中数据的完整性进行比较，结果如表1、图5 所示。

Table 1 Comparison of signature scheme simulation experimental data表1 签名方案仿真实验数据比较 单位：s

可以看出，无证书线性同态聚合签名方案在验证大量文件的完整性时所花费的时间远小于CLLHS。当验证数据块达到50个时，其验证速度较CLLHS 提高了近10 倍。原因在于对N个用户或审计者进行数据完整性公开验证时，如果使用CLLHS，则需要获得所有用户数据块的签名，并对签名逐一验证。随着待验证文件数据块个数的不断增加，用户在验证时的计算代价也会越来越大。而使用无证书线性同态聚合签名方案可极大减少验证时的计算代价。当用户或审计者想验证N个用户文件时，只需将每个用户数据对应的同态组合签名进行聚合，然后验证聚合签名的合法性即可。通过验证一个同态聚合签名是否有效，便可判定N个用户文件数据块是否保存完好。由此可见，使用无证书线性同态聚合签名方案对大量数据的完整性进行验证时，计算代价不随验证文件数据块数量的增加而显著增大，签名验证效率大大提高。

Fig.5 Comparison between CLLHS and scheme of this paper图5 CLLHS 方案与本文方案性能比较

7 结语

本文提出一种安全高效的无证书线性同态聚合签名方案，并给出了方案的安全证明。结果表明，该方案可以抵抗来自聚合签名者内部的“合谋攻击”。然而，云存储中还存在许多安全技术瓶颈需要解决，如多用户共享数据的权限问题、用户数据审计权限分配问题、各种侧信道攻击、密钥泄露等。这些问题对云存储系统的安全性是一个新挑战，对于密码学也是一个新课题，需要深入细致研究，才能充分保障用户云端数据的安全性。