基于ARIMA-BP 组合模型的货运量预测研究

曹 慧，秦江涛

（上海理工大学 管理学院，上海 200093）

0 引言

铁路货运量在我国运输行业的发展中扮演着重要角色，能够反映出我国交通运输行业现状及国民经济发展情况，同时也存在因运输设备不足而不能满足货运需求等问题，面临着公路、水路等其他运输方式的竞争。铁路相关部门需要制定灵活的运输计划，优化铁路运输问题改善竞争局面，这就需要通过对货运量进行预测，掌握一定时期的货运量以判断我国铁路货运发展趋势和未来经济发展，制定相关计划以解决问题。

常用的货运量预测方法有很多，比如时间序列分析、神经网络方法、灰色预测等。时间序列分析是最常用的分析方法，其中ARIMA 最具代表性，对线性的数据具有较高的拟合度，而对于非线性的数据信息不能进行很好的预测。通常情况下，时间序列数据包含线性和非线性部分，因此仅通过ARIMA 模型对数据进行线性预测，得到的结果往往不能满足人的需求。BP、RNN、LSTM等神经网络方法中应用较为广泛的为BP 神经网络，广泛应用于股票、二手房、碳市场等领域，对于解决非线性时间序列问题具有很好的效果，同时也具有过拟合、梯度消失、隐含层的选择等问题。灰色预测计算工作量小、预测精度高，但过于依赖初始值和背景值。

在上述预测方法中，大多数学者采用单一模型对数据进行预测，比如孙斌等使用ARIMA 模型对极端事件下货运量进行线性预测，发现ARIMA 模型货运量的线性部分具有较高的拟合；谭雪针对货运量具有高度非线性和不确定性的特点，运用GRU 模型对数据进行单步和多步预测，结果表明GRU 可较好拟合货运量的非线性特征，但忽略了数据的线性特征。传统单一模型主要是对于因果关系和时间序列模型分析无法提取较为全面的数据信息。随着研究的深入，学者们开始对组合模型进行研究，例如梁宁等分析货运量与影响因素的非线性关系，使用GRA确定影响因素的权重，采用FOA 选择SVM-mixed 的最优参数，提高结果精确度；耿立艳等提出使用（FOA）算法优化选择混合核LSSVM 参数并应用于货运量预测，相比使用单一LSSVM，精度得到了提高。在这些组合模型中，常见的是引进一种算法优化另一种算法的参数以提高精度，但参数过多可能会导致参数组合数量过多，同时忽略数据本身的线性和非线性的结构特点，导致信息提取不全面、结果不理想。通过分析可知，铁路货运量包含线性和非线性部分，本文选取对线性部分具有较高拟合度的ARIMA 模型和对非线性部分解决效果较好的BP 模型，并将其组合提出ARIMA -BP 加权组合模型和ARIMA -BP 残差优化组合模型，将货运量中线性与非线性部分进行细化，充分提取数据信息，并应用于铁路货运量研究，进行模型对比分析以探究方法的可行性。

1 理论模型

1.1 ARIMA 模型

ARIMA（p，d，q）模型即差分自回归移动平均模型，是时间序列分析方法中常用模型之一。AR 是自回归，p 为自回归项；MA 为移动平均，q 为移动平均项，d 为时间序列平稳时所做的差分次数。此模型是根据历史数据预测未来数据，对数据的线性部分进行较好拟合，但对于非线性部分的拟合效果欠佳。一般形式可表示为：

其中，X为当前值，μ 为常数项，p 为自回归项，γ是自相关系数，｛ε｝是残差序列，q 是移动平均项，θ是移动平均项系数。

使用此模型对铁路货运量进行预测的基本程序为：①判断货运量数据的平稳性，通过对数据作散点图，自相关（ACF）和偏自相关（PACF）函数图以及ADF 单位根检验，可知原始数据是否平稳，若原始数据不平稳，对其进行差分；②模型定阶，对ARIMA（p，d，q）模型定阶，确定p、d、q 3个参数的值，对货运量的自相关（ACF）和偏自相关（PACF）图进行分析，初步判定参数，再根据信息准则函数法AIC 准则判定最优的阶数组合；③进行模型拟合，得到模型参数，作残差检验，判断是否为白噪声，进行模型预测。

上述步骤使用ARIMA 模型对铁路货运量进行线性部分建模分析，但忽略了货运量非线性部分，对数据信息提取不充分。

1.2 BP 神经网络

BP 神经网络是一种前馈网络，BP 神经网络包括三层，即输入层、隐含层、输出层。BP 神经网络的传递过程主要分为正向传播和反向传播，正向传播是从输入层开始经过隐含层，最后到输出层；如果输出结果没有达到预期，则进行反向传播，从输出层开始经过隐含层，最后到输入层，在此过程中主要使用梯度下降方法，依次调节隐含层到输出层的权值，以及输入层到隐含层的权值，使得预测值不断逼近真实值。

BP 神经网络的一般形式如下：

其中，X为输入量，Y为输出量，

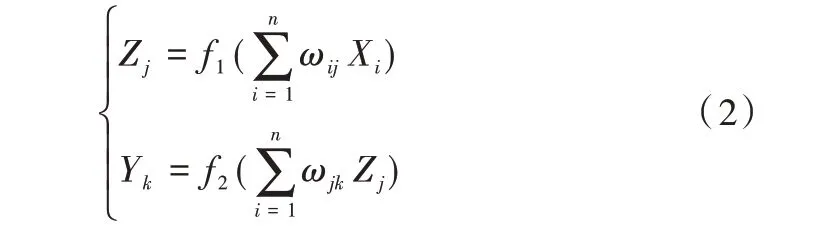
ω

(

i

=1,2…

N

;

j

=1,2…

N

)为输入层和隐含层之间的权值，

ω

(

k

=1,2…

N

)为隐含层和输出层的权值，f和f为神经网络的激活函数。

BP 神经网络可以很好地解决数据的非线性问题，对于具有线性和非线性特点的铁路货运量，BP 神经网络可以弥补ARIMA 建模过程中所忽略数据的非线性信息。

1.3 ARIMA-BP 组合模型

ARIMA 模型和BP 神经网络都具有各自优势，但应用单一模型得到的结果无法达到人们预期。因此，本文提出利用ARIMA-BP 组合模型对中国铁路货运量进行预测，使两者优势互补。分别对数据的线性部分和非线性部分进行建模分析，从加权优化和残差优化的角度进行组合模型预测，并应用于铁路货运量预测研究。

1.3.1 ARIMA-BP 加权组合模型

利用ARIMA 和BP 分别对原始数据进行预测，分别得到预测值，通过简单加权法对单一模型的预测值进行加权处理。基本思想为单一模型预测结果误差的方差越小，说明该模型的预测精度越高，反之就越低。加权法的基本过程为：Y为实际的时间数据序列，ARIMA 模型得到预测值F，BP 模型得到预测值F，通过简单加权预测得到的货运量预测值F，ω和ω分别为ARIMA 和BP 模型在组合预测中的权重。因此，ARIMA-BP 加权组合模型的预测值可表示为：

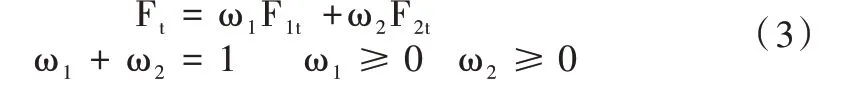
1.3.2 ARIMA-BP 残差优化组合模型

残差优化是一种“误差补偿”的思想，第一种模型得到的预测值与真实值的误差输入到第二种模型进行残差优化，使两种单一模型充分发挥各自优势，实现优势互补。本文将其应用于铁路货运量研究中，假设铁路货运量时间序列为Y，由线性部分与非线性两部分组成，则ARIMA-BP 残差优化组合模型构建步骤如下：

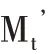
1.4 评价指标

评价指标使用平均绝对误差MAE、平均绝对百分比误差MAPE 和均方根误差RMSE，为衡量模型精度的常用指标，MAE、MAPE 和RMSE 越小，即误差越小，模型预测精度就越高。每个指标计算公式如下：

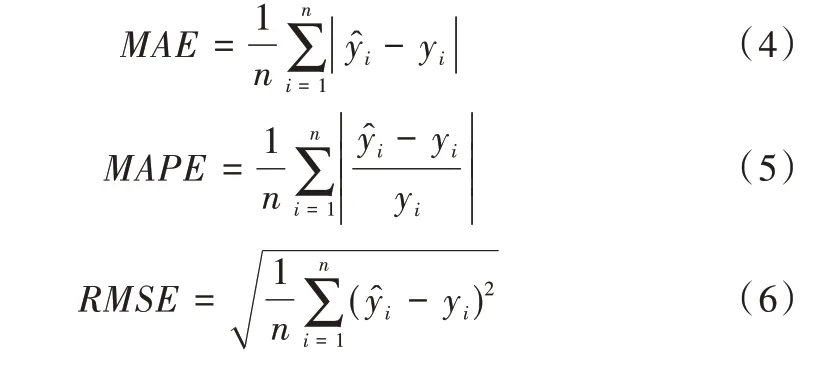
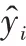
2 实证分析

本文选取中国铁路货运量1980-2020 年的数据进行建模分析，数据来源为国家统计局中国统计年鉴。

2.1 ARIMA 模型预测

2.1.1 数据平稳性判断

判断数据平稳性，对铁路货运量原始数据做序列图，原始序列图数据波动较大，是不平稳序列。本文选取差分的方法对其进行平稳化处理，得到一阶差分序列图P>0.05序列不平稳，因此进行二阶差分，序列在零上下波动，并且进行单位根检验可得t 统计量的值均小于3个显著水平的单位根检验的临界值，p 值为0.000 0<0.05，说明不存在单位根，是平稳序列。

Table 1 Second-order difference ADF test results表1 二阶差分ADF 检验结果

2.1.2 模型定阶

从上文可知，二阶差分后序列平稳，因此d=2。通过对序列二阶差分的自相关（ACF）和偏自相关（PACF）图进行分析可以看出，自相关和偏自相关系数都在二阶之后落入置信区间，因此判定所建模型为ARIMA（2，2，2）。

2.1.3 模型拟合

基于模型ARIMA（2，2，2）对数据进行拟合得到模型参数，并且都通过了显著性检验，结果如表2 所示，由此可得ARIMA（2，2，2）模型。

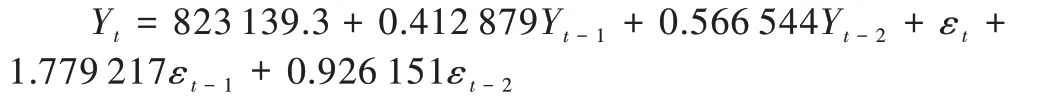
Fig.1 First-order difference ACF and PACF diagrams图1 一阶差分ACF 图及PACF 图

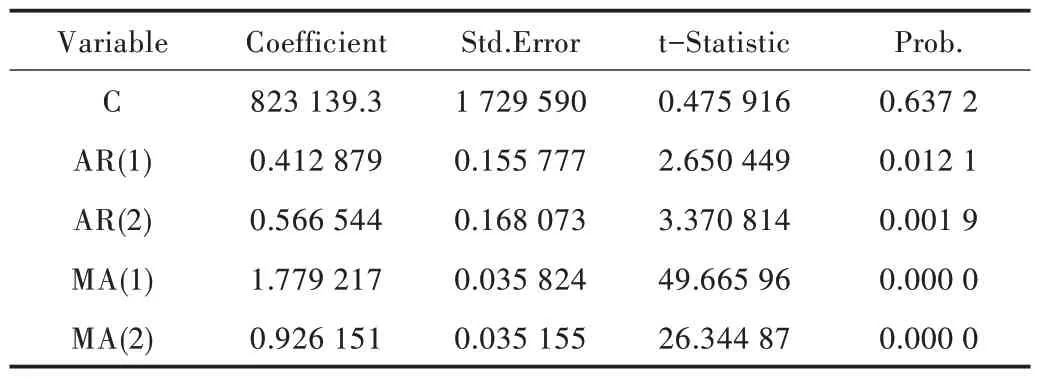
Table 2 Parameter estimation results of ARIMA（2，2，2）model表2 ARIMA（2，2，2）模型参数估计结果

2.1.4 残差检验

模型可行性判断还需要进行残差检验，通过对残差的自相关和偏自相关检验发现，p 值都大于0.05，说明残差部分不相关，模型拟合度较好，检验通过模型可用于预测。

2.2 BP 神经网络预测

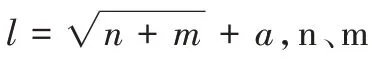
2.3 组合模型预测

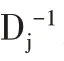
BP 残差优化与上文通过BP 对铁路货运量原始数据进行建模训练过程一样，通过ARIMA 模型预测，得到铁路货运量真实值与预测值的残差，通过BP 神经网络进行训练，得到残差的预测值，将得到的残差预测值与ARIMA 模型预测值相加，得到组合模型的预测结果。

2.4 模型结果分析

4 种模型的预测结果如图2—图5 所示。从单一模型看，ARIMA 和BP 神经网络的预测值与实际值的变化趋势总体保持一致，在2010 年以前预测结果和真实值拟合精度较高，而在2010 年以后，虽然变化趋势一致，但预测结果和真实值相差较大。图3 为ARIMA-BP 加权组合模型的预测结果，其结果比单一模型更接近真实值，2010 年以后的预测值与真实值的波动程度也较小。从图4 可以看出，ARIMA-BP 残差优化组合模型相比其他3 种模型整体精度更高，并且2016 年以后的预测值和真实值的曲线几乎重合。

Fig.2 ARIMA prediction results图2 ARIMA 预测结果

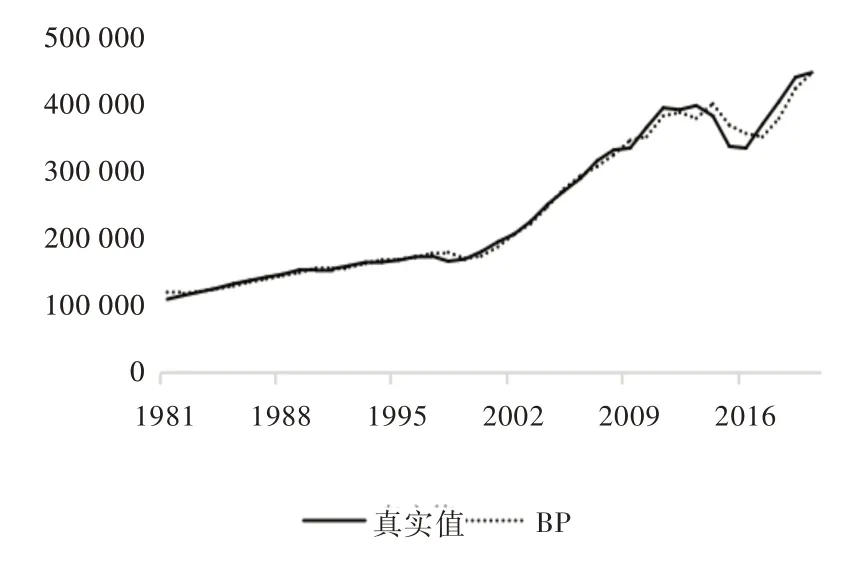
Fig.3 Prediction results of BP neural network图3 BP 神经网络预测结果

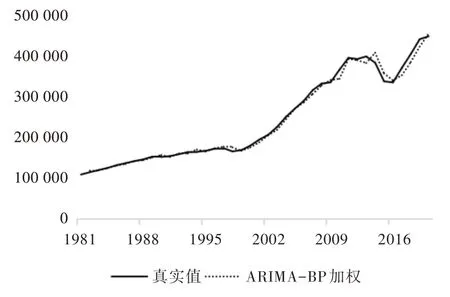
Fig.4 ARIMA-BP weighted prediction results图4 ARIMA -BP 加权预测结果

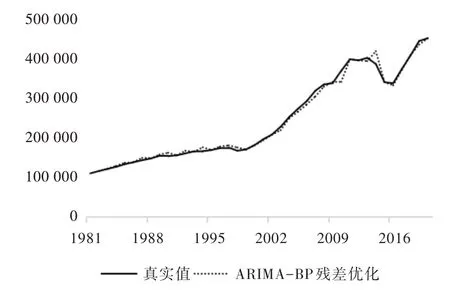
Fig.5 Optimized prediction results of ARIMA-BP residuals图5 ARIMA -BP 残差优化预测结果

根据表3 比较4 种模型的评价指标，两种单一模型相比，预测结果相似，但ARIMA 比BP 的3 种评价指标低224.33、0.05%、500.08；两个组合模型和两个单一模型相比，组合模型的表现效果都比单一模型的表现效果好；两个组合模型相比，ARIMA-BP 残差优化模型预测精度最高、误差较小，MAE MAPE RMSE分别为5135.90、0.0209、8462.49，比另一种加权组合模型的3 种评价指标低1 286.04、0.23%、812.77。

整体来看，4 种模型在铁路货运量预测方面的表现都较好，MAPE 的值都保持在5%以内，而残差优化的组合模型精度最高、误差最小。

Table 3 Evaluation indexes of the model表3 模型的评价指标

3 结语

本文针对铁路货运量的年度历史数据及其本身特点，使用时间序列及神经网络方法，将ARIMA 模型和BP 神经网络通过不同的方式进行组合，得到ARIMA-BP 加权模型和ARIMA-BP 残差优化模型，分别对铁路货运量数据的线性和非线性部分进行建模并与ARIMA 模型和BP 神经网络传统单一模型进行对比。试验结果表明，组合模型结果优于单一模型，并且ARIMA-BP 残差优化模型的预测精度最高。

本文重点关注的是货运量数据本身的线性和非线性关系，但铁路货运量受到很多因素的影响，比如节假日、货运价格等，下一步将相关影响因素纳入模型中，完善模型，进一步提高预测精度。同时，本文构建的模型在铁路货运量预测方面有效，但是对于其他领域数据预测的有效性还有待验证。此外，本文设计的组合模型由两个单一模型构成，可以考虑引入其他模型建立新的组合模型，以丰富理论模型，使结果更加准确。