改进LSTM 的脱轨系数预测方法

张 卜，刘怡伶，张文静，刘学文

（上海工程技术大学机械与汽车工程学院，上海 201620）

0 引言

随着社会经济的不断发展和铁路技术的不断提升，轮轨列车的运行速度至今已达到每小时500 多公里，运载重量也在逐渐增加，但随之而来的列车运行安全成为最棘手的问题之一，其中最为危险的工况就是脱轨。

在轨道交通建设领域，轮轨之间的作用研究自始至终是车辆—基础耦合动力学的核心所在。理清轮轨在不同工况、不同运行状态等条件下的接触状态，是研究轮轨作用的焦点问题。随着深度学习理论的迅速发展，除直接以理论方法研究脱轨机理外，也可以通过深度学习方法挖掘大数据中的潜在规律，Sitton 等建立多个BP 网络分别加以训练，网络收敛后将预测结果与验证集进行比较，根据网络性能表现对它们赋予权重，将多个带权重的BP 网络组成投票系统以预测货冲击对轨、桥带来的破坏；Samira 等和Serdar 等在神经网络基础上，建立一种新的预测模型，用于列车脱轨事故风险评估；Dindar 等设计一种由贝叶斯分类器（NB）组成的网络，该网络上层NB 的分类结果会成为下一层NB 的输入，可对因极端天气造成的脱轨事故进行准确分类；Zhang 等利用深层信念网络（Deep Belief Network，DBN）对列车运行安全性进行预测，并且考虑乘客舒适性；张俊甲等利用附加权重法对BP 神经网络进行改进，克服了传统BP 网络学习率调节困难的缺点，得到一种能够有效预测脱轨系数的网络模型；陈皓等建立基于BR网络的NARX 网络预测模型以预测列车脱轨系数，解决了传统BP 网络预测脱轨系数成本高、精度低的问题；杨桐等采用T-snake 模型分析轮轨接触图像，推算出轮轨相对横向位移量，结合遗传算法优化小波神经网络，对相对位移、速度、加速度以及轮重减载率和脱轨系数间的映射进行建模。

列车运行时所产生的各项数据按照被采样的先后顺序记录下来，是典型的时间序列。时间序列的特殊性在于其中的各样例不是孤立的，之前的样例会影响后面样例的状态，长短时记忆神经网络（LSTM）所具有的循环结构使它能够掌握样例间的关联性。陈渝等采用LSTM 对医院门诊量数据进行建模，取得了较好的预测精度；李彬等借助随机梯度下降法对LSTM 进行优化，对风力发电功率概率进行预测，得出一种能够预测未来200h 风电功率概率函数的神经网络；Ugurlu 等以均值绝对误差（MAE）和均方根误差（RMSE）作为性能度量，使用LSTM 精确预测了电价的价格滞后现象。

要想保证深度学习效果，需要准备大量的训练数据，然而列车实车试验成本高昂，铁路日常运营中收集到的数据，一般研究机构也难以获得，通过仿真方法获取数据集是解决该难题的方法之一。近年来，仿真软件的性能逐步提升，其中SIMPACK 在多体动力学，尤其是轮轨接触方面的仿真效果非常好。陈杨在多体系统动力学软件SIMPACK 中建立了整车动力学仿真模型，并对轮轨接触面和悬挂系统做了处理，加入了轨道不平顺激励模型，得到了较为真实的仿真场景，利用仿真研究了各向不平顺对蛇形失稳临界速度的影响；王海涛在SIMPACK 中建立了车—线—隧刚柔耦合动力学模型，利用仿真与实测数据研究了车轮抬升力，车轮踏面磨耗数与隧道壁振幅等参数对列车运行的影响；何银川在SIMPACK 中建立了驮背运输车辆系统振动模型，根据仿真分析了临界速度、曲线通过能力和悬架对垂向稳定性的影响，并且做了实际试验，与仿真结果是相吻合的；姚常伟通过FLUENT、ANSYS 和SIMPACK 等仿真软件对受侧风影响的列车模型进行了仿真，仿真结果与通过理论计算得到的风载荷对车辆的影响是等效的。

上述科研成果都能证明SIMPACK 多体动力学仿真软件在研究轮轨接触方面的可靠性，因此借助仿真工具得到数据集，再利用深度学习方法分析数据，从而得到关键参数与列车轮轨状态之间的关系是可行的。

本研究采用SIMPACK 仿真软件收集列车通过弯道时的各项参数，包括最大脱轨系数、最大横向振动加速度、横向重心偏移量、车速、弯道半径和轨道超高，组成训练数据集。

循环神经网络，特别是其中的长短时记忆神经网络已被诸多研究证实适用于处理时间序列数据，因此本研究也将以长短时记忆神经网络作为基础模型。但是一方面，长短时记忆网络训练过程对学习率非常敏感，学习率的调整往往要根据学者的经验或反复尝试才得以确定，这样调参不仅要耗费大量时间，也未必能达到最优效果；另一方面，得益于长短时记忆网络强大的学习能力，网络可以高效地从训练集中找到属性与标记之间的映射，但是训练后的网络在测试集上的表现往往不如训练集，也即发生了过拟合现象。针对这两种情况，本研究提出使用简便、有效的动态学习率和Dropout 方法针对学习率和网络结构进行优化，将经过改进的长短时记忆神经网络用于列车通过弯道时的脱轨系数预测。实验结果表明，改进的长短时记忆神经网络能够较好地预测脱轨系数随工况变化趋势，为进一步的脱轨系数预测研究提供了支持。

1 长短时记忆神经网络（LSTM）

1.1 LSTM 神经网络

LSTM 神经网络改良于循环神经网络（RNN），除了与RNN 相同的外部循环外，还有本身节点间的自循环。自循环由遗忘门、输入门和输出门控制，这三者可根据当前时刻的输入从隐层中删除、添加、提取信息，改善了RNN 长期依赖导致梯度消失和梯度爆炸的问题，图1 展示了LSTM 的单元结构。

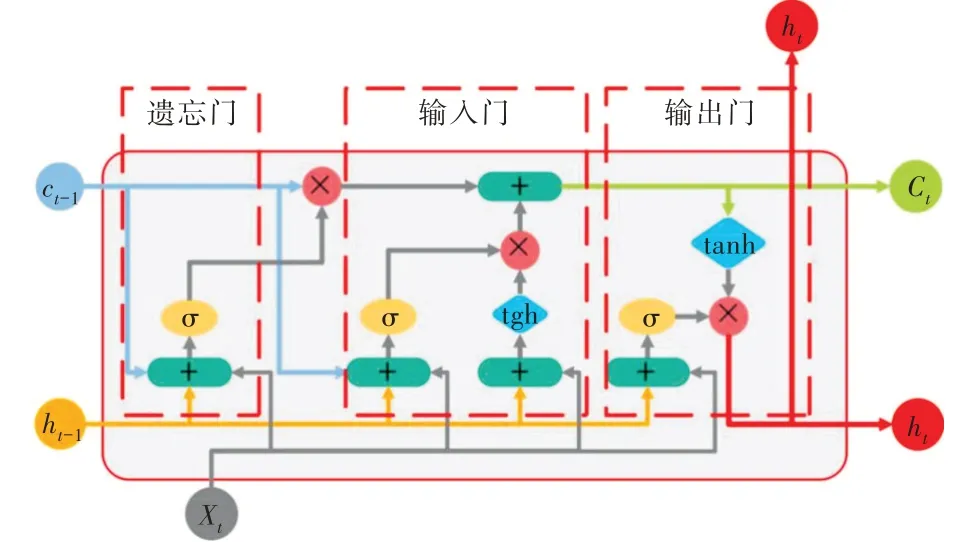
Fig.1 Unit structure of LSTM图1 LSTM 的单元结构

输入门根据

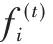
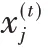
x

、输入门的输入偏置

b

和

h

决定计算当前时刻输出的状态

c

(，可用式（2）计算。其中，

U

为单元体输入门的输入权重，

W

为单元体输入门的循环权重，Sigmoid 为激活函数，则：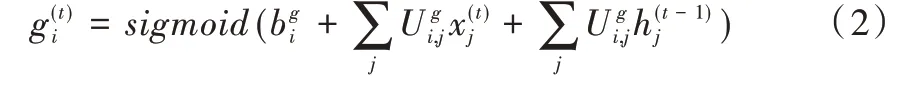

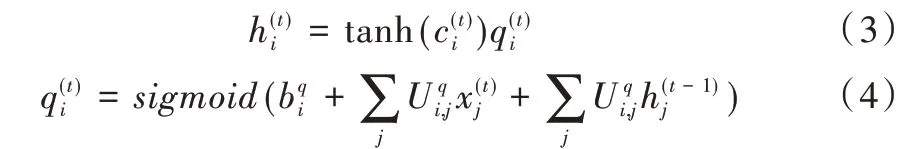
1.2 动态学习率方法

神经网络的权重更新离不开梯度下降法，传统的梯度下降方法如式（5）所示。其中，

W

为第

i

次更新时的权重，

η

为学习率，

L

为损失函数的值。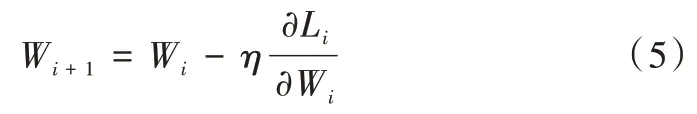

学习率

η

的取值对网络训练效果影响很大，取值过大会导致更新跳过最优权重，或是损失函数震荡，网络难以收敛，取值过小会导致网络收敛慢、训练效率差。为解决该问题可以引入动态学习率方法，每轮训练都根据当前损失函数的梯度Δ

L

重新分配下一轮训练的学习率，其计算方法如式（6）所示。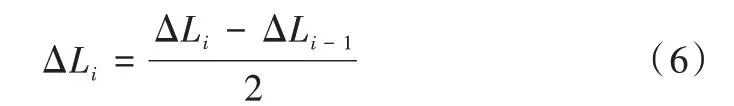

动态学习率可按式（7）推导，可以看出，随着训练轮数的增加，动态学习率会越来越小，防止越过最优解，但当Δ

L

≤0 时，即网络尚未出现收敛趋势时，动态学习率的降低速度会变慢，以保证网络训练效率。若学习率过低，会引发梯度消失问题，因此

η

不会小于0.01 。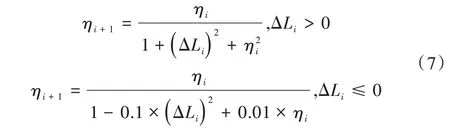

1.3 Dropout 方法

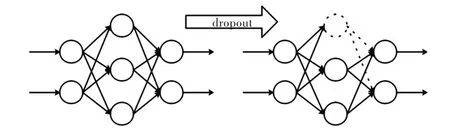
Fig.2 Principle of dropout图2 Dropout 原理

2 数据集准备

2.1 SIMPACK 仿真场景

该仿真场景中包含模型与线路两个部分，其中模型中有17个刚体、1个车身、2个构架、4 组轮对、8个轴箱和2个摇枕。其中，车身、构架和轮对考虑到了前后伸缩、左右晃动、上下浮动以及点头、摇头和翻滚6个自由度，轴箱考虑点头，只有1个自由度，摇枕与车身刚性连接，不考虑其自由度，故该模型共有50个自由度。该模型包含54个力元，因只考虑单节车辆，故没有车钩力，其中轴套与构架间使用43 号力元，一系悬挂中的弹簧使用85 号力元，一二系悬挂中的阻尼以及蛇形减振器选用6 号力元，二系悬挂的两个剪切弹簧使用79 号力元，车架与摇枕之间用13 号力元作为缓冲器以防止二者碰撞，轮轨接触力元采用78 号力元并考虑到了它的非线性特性，该模型如图1 所示。

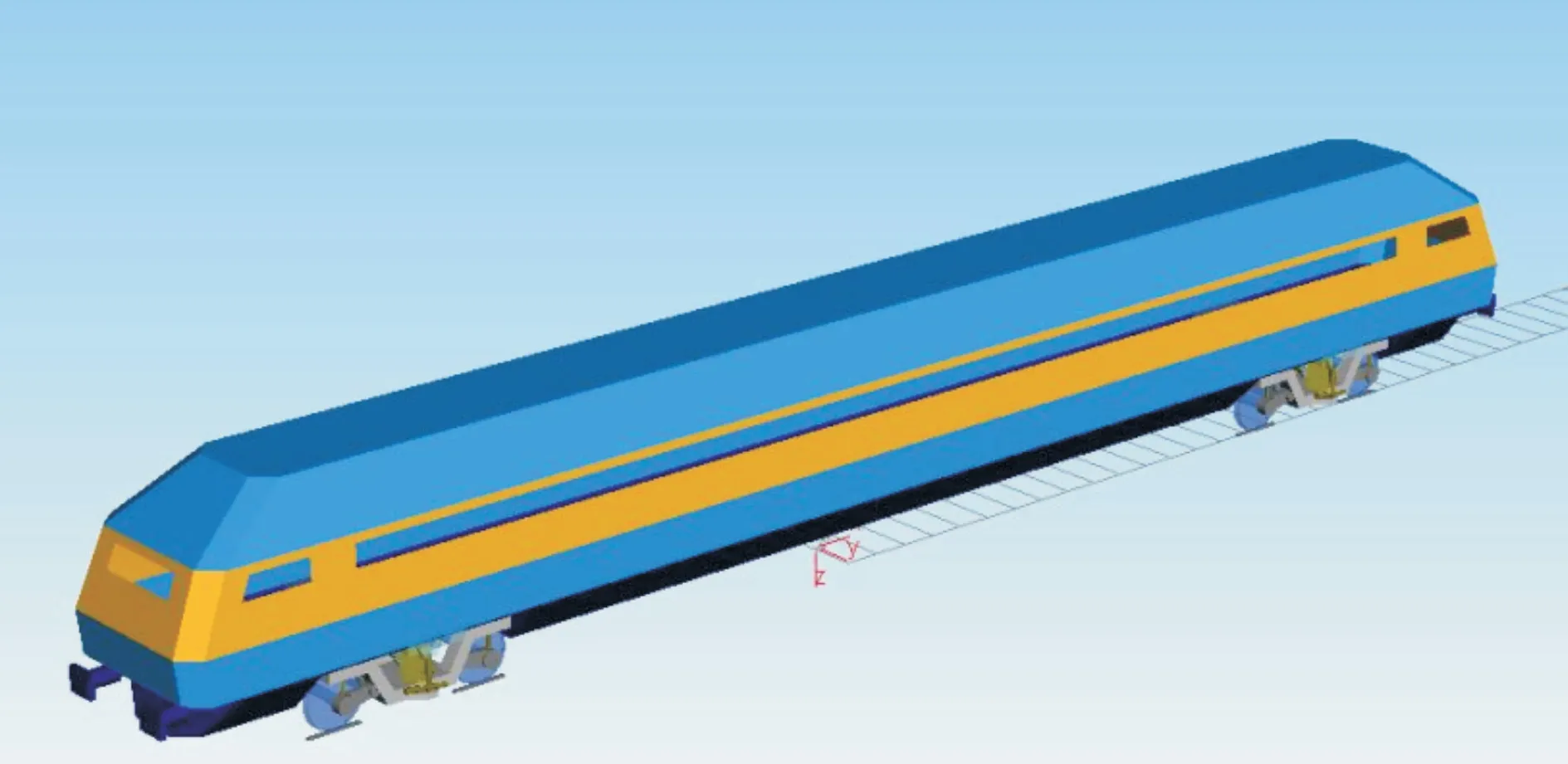
Fig.3 SIMPACK simulation model图3 SIMPACK 仿真模型

车辆行驶线路包括：直线—过渡曲线—弯道—过渡曲线—直线，列车在直线的行驶状态不是研究重点，故设置为10m，过渡曲线用线性过渡，长度为10m，弯道的长度为500m，半径可调。引入的轨道水平不平顺激励参考美国6 级谱，式（8）是其谱密度分析式，各参数如表1 所示。

Table 1 Parameter values of the six-order spectrum of the US orbit表1 美国轨道六级谱的参数值

2.2 数据集及其预处理

列车在弯道上的脱轨系数，会受到线路、车速等众多因素的影响，本文将重点放在车速、重心横向偏移量、半径和超高上，研究这三者对脱轨系数的影响。通过不同条件下的仿真实验，提取车速、半径、超高、重心横向偏移量作为属性，对应的脱轨系数作为标记，共得到如表2 所示的1 269 条样例。其中，超高按照式（9）计算，一般应该按5mm的整倍数设置，且按照国家标准一般不能超过120～150mm，但为了在仿真中能得到尽可能大的脱轨系数，暂不考虑这些限制。

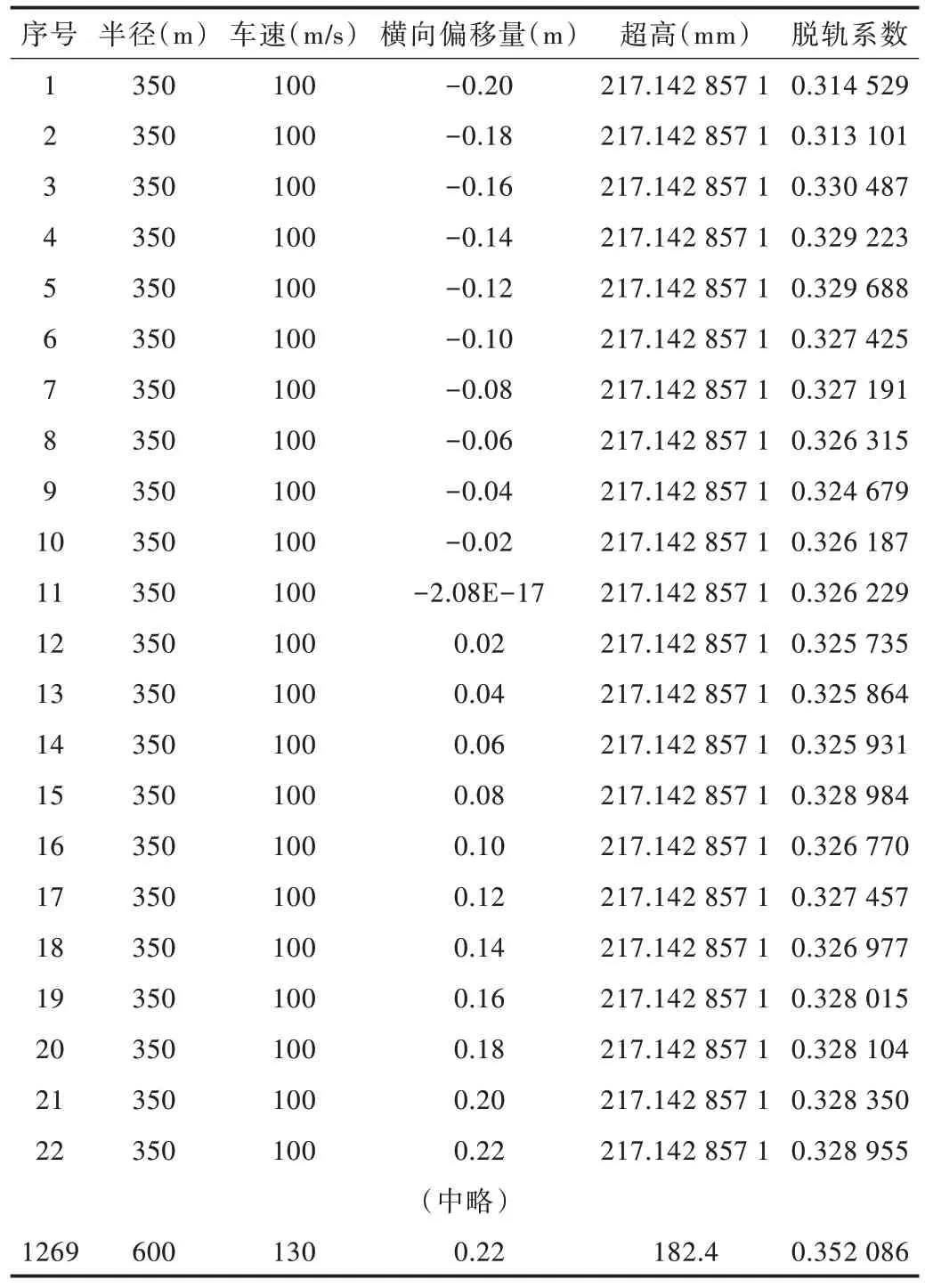
Table 2 Derailment coefficient data set表2 脱轨系数数据集

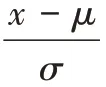
3 脱轨系数预测

3.1 评价标准

为了评估模型最终在测试集上的表现，采用均方根误差（RMSE）作为评价标准，如式（10）所示，其为各条样例预测值和真实值偏差的平方之和的平方根，反映了预测值偏离真实值的程度，当预测值出现较大误差时，会导致RMSE 激增，故RMSE 能够较为全面地反映预测的精确程度。

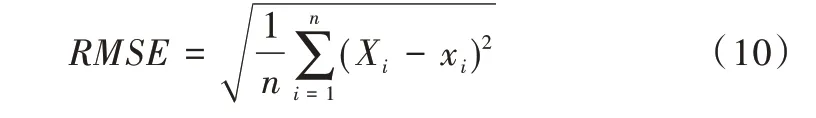
3.2 实验结果与分析

将数据集的前890条作为训练集，其余作为测试集。初始学习率为0.01，循环次数500次，batch_size 为20，keep_prob 参数决定了dropout 层保留输出权重的概率，设置为0.9、0.8、0.7，即单元有10%、20%、30%的概率失活，分别进行训练，选取测试结果较好的一种作为最终参数。3 种使用不同keep_prob 参数的LSTM 在训练集上都有不错的表现，图4 展示了500 轮训练中，损失函数值变化曲线。

Fig.4 Loss function in training图4 训练中的损失函数

几种不同Keep_Prob 参数下的LSTM 在测试集上的RMSE 如表3 所示。传统的LSTM 虽然在训练集上表现优异，但在测试集上的误差反而较大，出现了过拟合现象。引入Dropout 方法，设置keep_prob 为0.9 和0.8 时，过拟合现象有所改善，但进一步减少保留输出权重的概率时，测试集上的误差再次增加，出现了欠拟合趋势。因此，最后选取Keep_Prob 参数为0.8。

Table 3 Prediction errors of different keep_prob parameter networks表3 不同keep_prob 参数网络的预测误差

最终测试结果如图5 所示，模型经过优化后有着较好的拟合精度，预测曲线虽然未和真实值完全重合，但是模型准确预测出了脱轨系数随工况的变化趋势。其中，在113 号样例附近，模型准确地预测出了因为车速突然下降而导致的脱轨系数断崖式下跌，在其他位置模型也把握住了车速越高、弯道半径越小，则脱轨系数越大的特点，这一特点在测试集和训练集上都相同，说明模型具有了较好的泛化性能。总体而言，虽然预测值和真实值之间有一定误差，但均方根误差控制在了0.01 以内，与未经优化的LSTM预测结果相比，改善较大，RMSE 减小近24%，对于预测脱轨系数的变化趋势有一定参考价值。

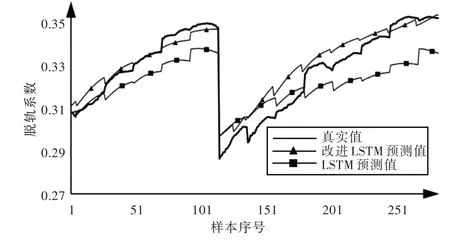
Fig.5 Prediction results of 2 kinds of LSTM图5 两种LSTM 预测结果

4 结语

列车脱轨系数是评价列车运行安全的重要参考，影响着轨道运输的设计、实验、运维等方方面面。本研究针对在弯道上受重心偏移量影响的列车脱轨系数，使用深度学习方法，建立长短时记忆神经网络进行脱轨系数预测。为了解决模型学习率调整困难的问题，引入了动态学习率方法，为了解决过拟合问题，使用了Dropout 方法。验证集表明，虽然在预测精度上仍有可以改善的地方，但通过优化，模型在验证集上的RMSE 减小了23.9%，不仅较好地预测出脱轨系数变化趋势，也把握住了脱轨系数骤然变化情况。总体而言，这种优化的长短时记忆网络时间序列预测方法能应用在脱轨系数预测上，能够为铁路安全运营提供数据支持。下一步研究将考虑更多因素对脱轨系数的影响，比如车轮抬升量、车钩力及横风等，并尝试采用其他优化方法以建立更加准确的预测方法，进一步挖掘列车运行数据的实用价值。