对中定位夹具运动分析及仿真

伞红军，徐洋洋，李鹏宇，陈久朋，陈 佳

（昆明理工大学机电工程学院，云南昆明 650500）

0 引言

近年来，随着人们生活水平的提高，越来越多人对显示器质量及显示效果的要求也越来越高。回顾显示设备发展进程，人们始终追求的目标是更加真实的视觉体验感。液晶显示器是基于液晶光电效应的显示设备。目前，液晶显示器已逐步取代了传统笨重的CRT 显示器，成为主流显示设备。对中定位夹具作为机械生产加工过程中的辅助定位夹具，对液晶显示器生产过程中的零部件定位加工精度具有重要影响。

1 相关研究

20 世纪初，随着美国市场对汽车工业标准化产品需求的迅速增加以及福特公司大量流水生产线的出现，普通机床已不能满足要求，专用夹具的出现解决了这一难题，促使汽车的生产方式发生了革命性变化，产量大幅增长。在两次世界大战期间，武器装备的生产推动科技又一次进步，夹具的设计生产也随之逐步发展完善。英国华尔通公司设计制造了世界上最早的槽系组合夹具系统。此后，前苏联也推动大型槽系组合夹具的生产与应用，并创造了夹具租赁组装站这一创新并行之有效的服务形式。

目前，显示器的生产装配仍没有完整的自动化装配生产线，主要依靠人工完成装配。当今社会对显示器的需求量越来越大，为了加快生产、提高生产效率，以更好地满足市场需求，则需要改进传统的生产装配方式，实现自动化生产装配。其中，显示器定位夹具贯穿整个装配过程，装配生产线上定位夹具的设计与应用对于显示器自动化装配生产起到重要作用。

显示器装配是显示器生产过程中必不可少的环节，装配效率将直接关系到企业的经济效益。随着如今显示器功能愈发全面，其加工技术也逐渐进步，但装配技术发展较为缓慢，一直以来都是薄弱环节，故对显示器装配生产线进行改进具有实际意义。本文在一种自主设计的对中定位夹具基础上，对其进行正运动学与逆运动学分析，得到对中定位机构的位移、速度、加速度、角速度及角加速度曲线，从而检验对中定位机构能否满足设计要求。

2 对中定位机构运动学分析

2.1 对中定位机构几何模型

对中定位机构几何模型如图1 所示，其中曲柄与机架的连接铰链位于直角坐标系原点处，滑块的滑动导路与

x

轴重合。两曲柄长度分别为

L

和

L

，两连杆长度分别为

L

和

L

，与

x

轴的夹角为

θ

和

θ

，滑块B、C 距离圆点的长度分别为

S

和

S

。对中定位机构位于初始位置时，曲柄与

x

轴的夹角为

ψ

，曲柄转动时以角速度

ω

进行转动。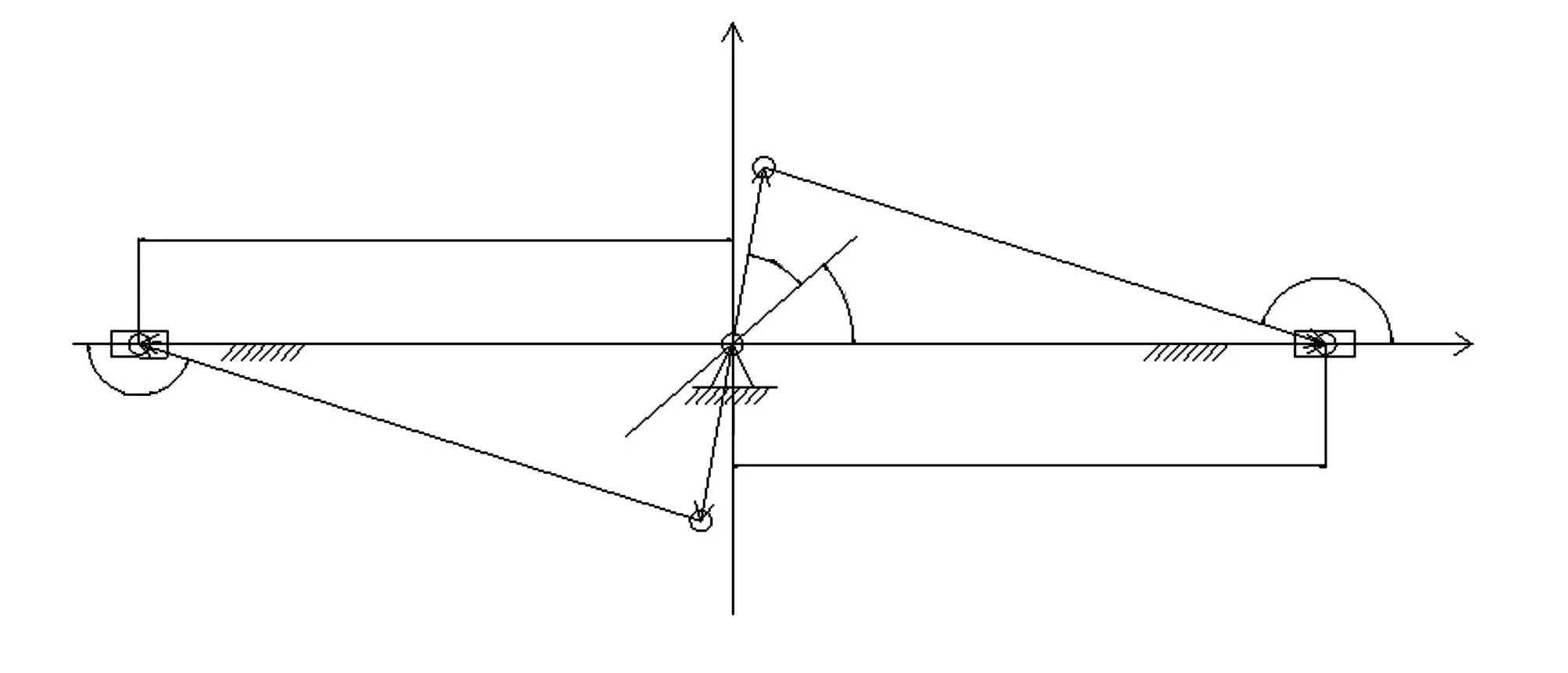

Fig.1 Geometric model of positioning mechanism motion process图1 定位机构运动过程几何模型

各构件的尺度参数和滑块行程用图1 中的符号表示，对中定位机构由连杆机构OAB 与OCD 两部分构成，通过曲柄OA 和OC 的旋转运动带动滑块B 与D 向中间靠拢，以此实现显示器在

x

轴方向上的对中定位功能。

2.2 正运动学分析

机构的正运动学分析是在已知输入构件的情况下，首先建立对中定位机构的矢量方程组，并对其在

x

轴与

y

轴上进行投影，得到机构的运动学位移方程组；其次，对位移方程组求微分，得到机构运动的速度方程组；最后，继续对速度方程组求微分，得到机构运动过程中的加速度方程组。

根据机构各构件矢量运算原理建立对中定位机构矢量方程组为：

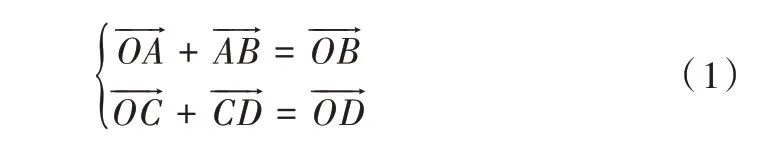
对式（1）所示的方程组分别向x 轴与y 轴投影，可得到如下矢量投影方程组：

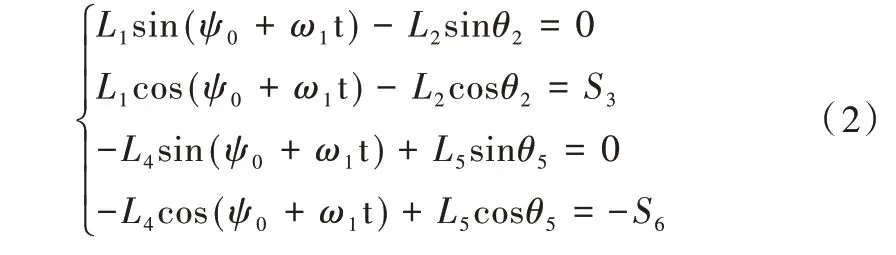
式（2）也称为对中定位机构的位移方程组，对其求解可得到滑块B、D 的行程及连杆AB、CD 与滑块导路构成的夹角，如下所示：

对式（2）的位移方程组求关于时间

t

的微分，可得到对中定位机构的速度方程组为：

对式（4）的定位机构速度方程组求解，可得滑块B、D的速度以及连杆AB 与CD 的角速度为：

继续对式（4）的速度方程组求关于时间

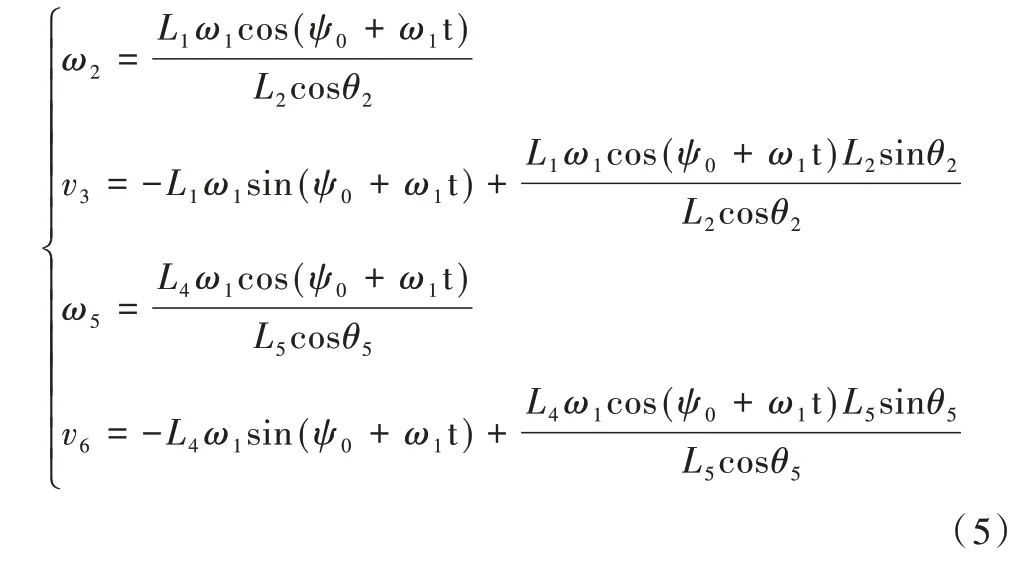
t

的微分，可得到对中定位机构的加速度方程组为：

对式（4）的定位机构速度方程组求解，可得滑块B、D的加速度以及连杆AB 与CD 的角加速度。

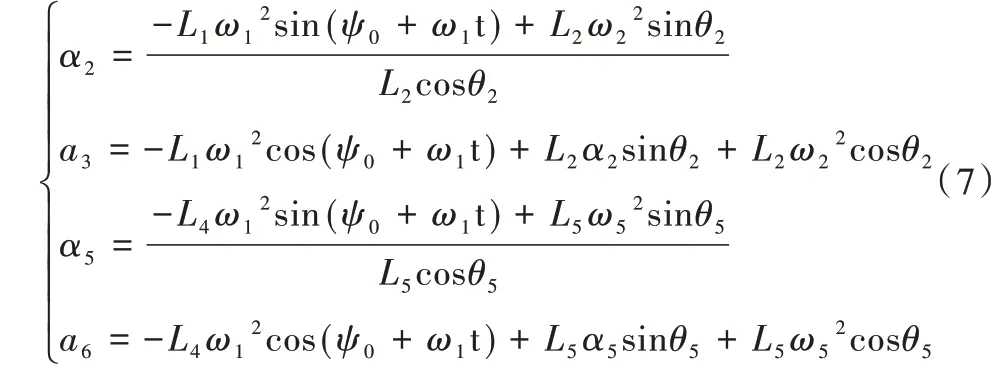
2.3 逆运动学分析

对中定位机构的正运动学分析是在已知输入构件的情况下，对机构在运动过程中各构件的运动学参数进行分析，从而使机构在运动过程中对显示器的夹持更稳定，减少夹持构件在夹持瞬间对显示器的冲击。

对定位机构的逆运动学分析过程进行建模，如图2 所示。

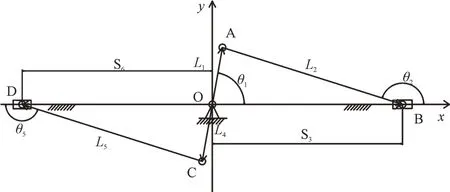
Fig.2 Geometric model for inverse kinematics analysis of positioning mechanism图2 定位机构逆运动学分析几何模型

为使定位机构快速地对显示器夹持定位，且尽量降低在夹持瞬间对显示器的冲击，设定滑块的运动参数为：滑块在启停时的速度为零，整个夹持机构的运动时间为1∕4s。

使用正弦函数实现滑块的速度变化规律，结合上述运动时间将滑块速度表示为：

对式（8）积分可得滑块的位移表达函数为：

结合显示器长度与托盘结构参数可设定滑块在启停时的位置分别为：S（0）=320mm，S（1∕4）=253mm，将滑块在启停时的位置参数带入式（8）、式（9）中，求解得到滑块的位移变化规律与速度变化规律：

对式（8）求导得到滑块的加速度变化规律：

在图2 所示的模型中，对

y

轴右侧的机构建立矢量方程：

对式（11）所示的方程分别向

x

轴与

y

轴投影，可得到如下矢量投影方程组：

式（13）也称为位移方程组，对其求解可得曲柄OA 转角和连杆AB 与滑块导路所构成的夹角，如下所示：

对式（13）的位移方程组求关于时间

t

的微分，可得到对中定位机构的速度方程组为：

对式（15）的速度方程组求导可得对中定位机构的加速度方程组为：

将滑块运动学参数的初始设定函数带入式（14）-式（16）中，可得到曲柄的运动参数，由此对整个机构进行运动控制。

3 运动学仿真及结果分析

3.1 虚拟样机仿真实验

虚拟样机技术广泛应用于机械制造、航空航天、船舶制造等领域，其通过建立虚拟样机模拟真实机构样机工作过程，并对机构构件在运动过程中的运动参数及受力情况作进一步分析研究，以此验证所设计机构的合理性。本文使用ADAMS 软件进行运动学仿真。

创建的连杆机构模型及添加约束后的模型如图3 所示。

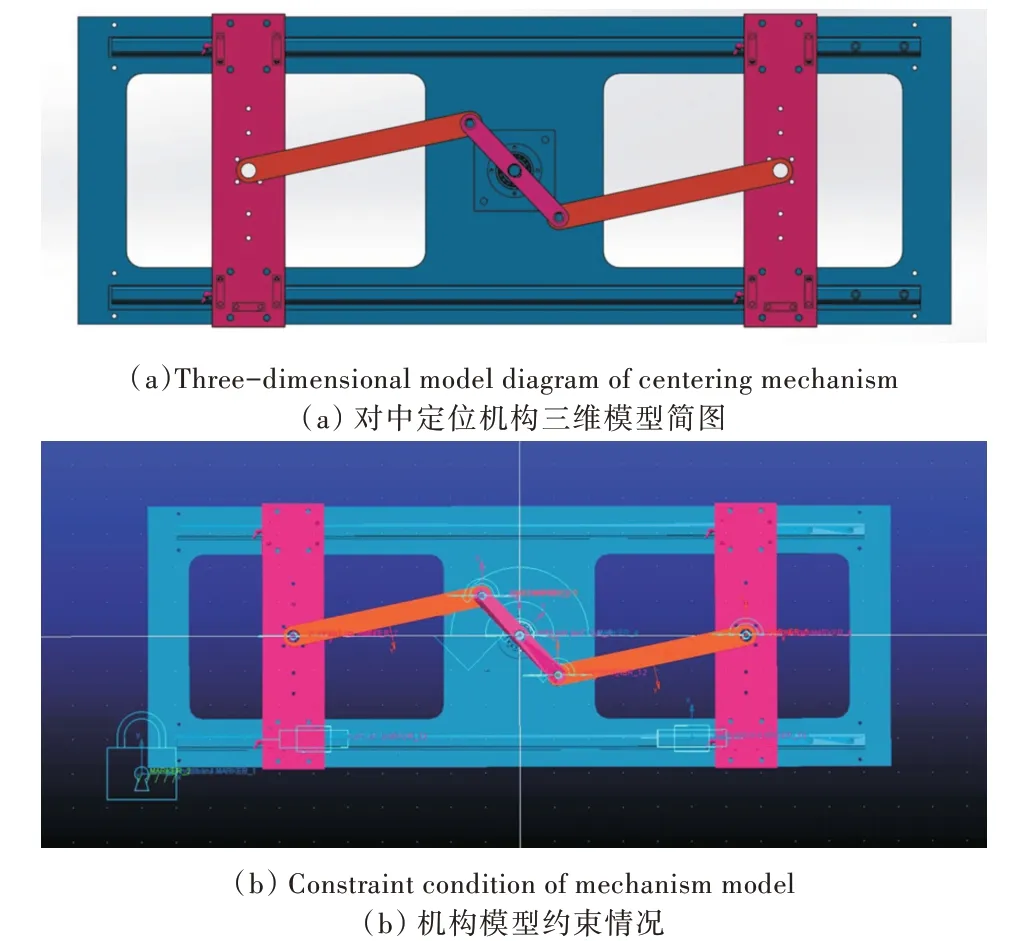
Fig.3 Centering mechanism diagram图3 对中定位机构

3.2 正运动学仿真结果分析

对虚拟样机模型进行仿真参数设置，令曲柄的驱动函数为匀速运动，并设置仿真时间，使得曲柄可运动5个周期。通过对模型的运动仿真可看到模拟机构运动过程，利用仿真运动的结果后处理工具得到各构件运动参数曲线图。两滑块的位移、速度与加速度曲线如图4 所示。

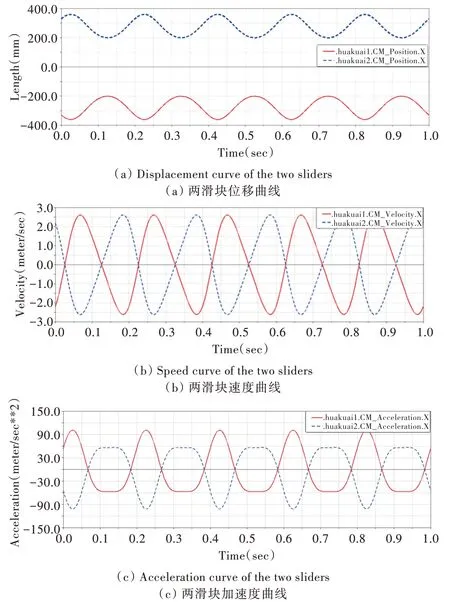
Fig.4 Curve of two sliders图4 两滑块曲线

由图4（a）所示的位移曲线图可清晰看出两个滑块在机构运动过程中的所处位置，完全满足对滑块的设计要求，即滑块要经过3个固定位置。图4（b）与图4（c）所示曲线比较平滑，且无尖点，表明对中定位机构在仿真机构运动过程中速度与加速度变化平稳，且没有出现突变，故在运动过程中不会产生较大冲击，具有良好的稳定性，进一步验证了该机构设计的合理性。

3.3 逆运动学仿真结果分析

机构在对显示器的夹紧定位过程中，为降低机构启动时滑块对显示器的冲击，在逆运动学分析中已规划了滑块运动函数，其速度与加速度曲线如图5 所示。通过规划后的滑块速度与加速度曲线可看出，滑块起步平稳，无较大冲击。

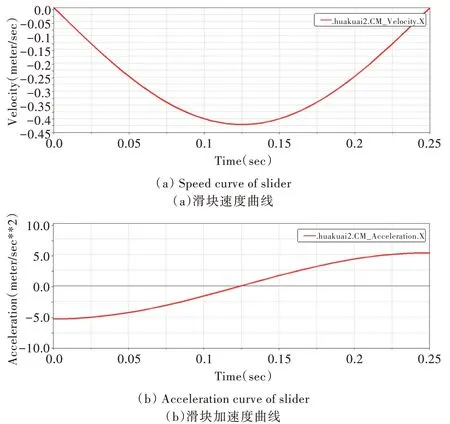
Fig.5 Velocity curve and acceleration curve of slider after planning图5 规划后的滑块速度曲线与加速度曲线

现将滑块作为驱动构件，驱动函数作为规划后的速度函数，并设置仿真时间为0.25s。通过仿真运动的结果后处理工具可得到各构件的运动参数曲线图，规划后的曲柄角速度与角加速度曲线如图6 所示。

为使滑块满足规划的运动规律，曲柄作为运动过程中的主动件，其运动过程需满足如图6（a）、图6（b）所示的速度和加速度曲线。由主动件曲柄的角速度和角加速度曲线可以看出：角速度和角加速度过渡平稳，无尖点和突变，曲柄规划的运动规律合理，且易于实现。

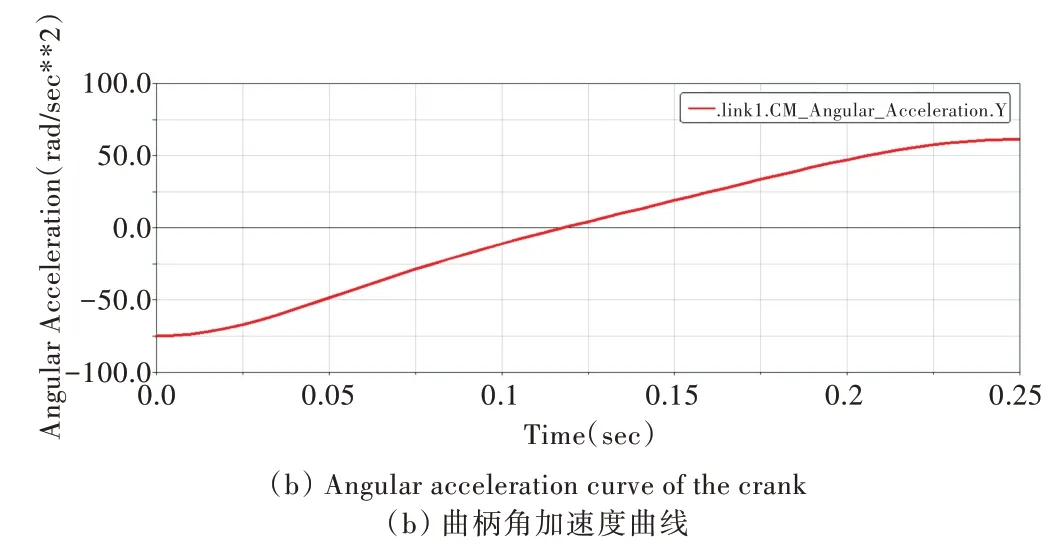
Fig.6 Curve of crank angular velocity and crank angular velocity after planning图6 规划后的曲柄角速度曲线与角加速度曲线

4 结语

本文针对设计的原理机构通过矢量封闭的方法得到机构位移方程，并对其求导得到机构的速度方程和加速度方程。求解各运动学方程，完成对中定位机构的正运动学与逆运动学分析，之后通过虚拟样机仿真实验对机构设计的合理性进行验证。用虚拟仿真软件ADMAS 得到滑块和曲柄的加速度及速度曲线，可看出曲线平滑，无尖点和突变出现，表明执行构件达到所设定的运动学要求，可作为液晶显示器生产线夹具设计的理论依据。但本文并没有对所设计的对中定位机构作动力学分析及仿真实验，这也是下一步的研究方向。