平面图形的静矩与惯性矩关系系数研究

俞晓明 ，陈 兰

1.盐城工学院 数理学院，江苏 盐城 224002；2.盐城市盐都区教师发展中心，江苏 盐城 224005

液罐半挂车是液体危险品道路运输的主要工具。当罐车上下坡时，液体系统的质心位置改变，导致汽车的轴荷分配等发生变化，从而对汽车的稳定性产生不利影响［1］，导致汽车侧倾事故的频繁发生［2-5］。因此，研究罐车系统的稳度具有重要的工程意义。

1 理论基础

对于矩形和立式圆柱液罐系统，其液位的高度计算较为简易，而两端为平盖的圆柱形或椭圆形的卧式液罐系统，液位高度的计算就比较复杂［6-8］。本文主要研究斜立式圆柱罐体系统的稳度问题。

1.1 模型假设

为研究方便，作如下假设：（1）液罐为圆柱形刚性容器，忽略车体的质量和尺寸，以及罐壁罐底的质量和厚度；（2）液罐与坡面间的摩擦系数足够大，以致汽车在坡面上行驶时液罐不下滑；（3）液面为水平，忽略液体表面张力引起罐内液面的凹凸；（4）液体为静态，忽略黏滞阻力以及振动等；（5）罐壁足够高，罐体处于临界倾角时罐内液体没有溢出。

1.2 力矩分析

装有一定量液体的圆柱形液罐静置在坡面上，液体模型如图1 所示、受力如图2 所示。设圆柱形液罐的直径为2R，坡面与水平面夹角为θ，液体的密度为ρ，重力加速度为g，液体与罐底面的交线MN 为y 轴，MN 的中点O 为坐标系原点，x 轴沿直径QP 方向，z 轴垂直于罐底面向上，如图1b所示。

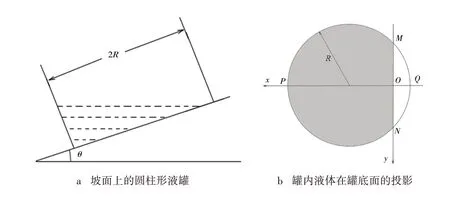
图1 坡面上圆柱形罐内的液体模型Fig. 1 Model of liquid body in cylindrical oil tan on inclined plane

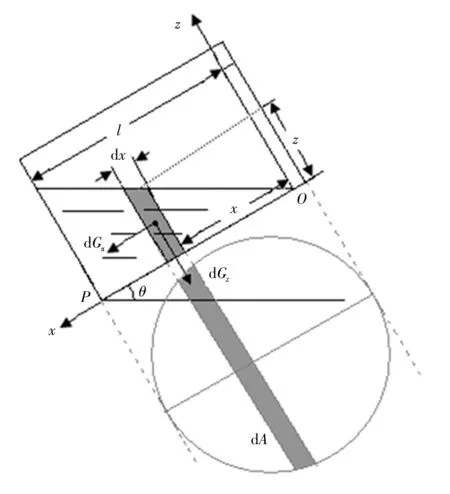
图2 坡面上圆柱形罐内液体的受力示意图Fig. 2 Stress diagram of liquid body in cylindrical oil tan on inclined plane

在xOy 平面内的x轴上距原点x处取宽度d x、高度z=x tan θ 的板形液体微元，其面积为d A、体积d V=x tan θd A、重力d G=ρgx tan θd A，则d G 的分量这两分量对过点P 且平行于y 轴的力矩分别为d MPy(d Gx)=则整个重力的分力矩及液体体积分别为：

式中：l为液体在罐底面上的投影在x轴上的长度，m；JOy=x2dA，为该投影对y轴的惯性矩，m4；SOy=xdA，为该投影对y轴的静矩，m3。

式（3）表明：圆柱形液罐内液体体积V等于液体在罐底面上投影的静矩Soy与坡面倾角正切值tanθ的乘积。

1.3 临界倾角确定

液罐不发生倾倒的条件为：

2 平面图形静矩与惯性矩关系系数

2.1 关系系数的定义

对于xOy平面内的图形K（图3），在K上任一点（x′，y′）处取面元dA，则K绕y轴、x轴的静矩和惯性矩分别为：

图3 平面图形KFig. 3 plane graph K

定义平面图形K绕y轴、x轴的静矩与惯性矩关系系数分别为：

式中：xmax、ymax分别为平面图形K在x、y轴上的特征长度，m。对于平面图形，如圆盘的直径、椭圆的轴长、矩形的边长以及等边三角形的边长等均为各自的特征长度。

根据静矩与惯性矩关系系数，式（5）可改写成：

式（11）表明，坡面上罐体的临界倾角取决于罐内液体在罐底面上投影的静矩与惯性矩关系系数。因此，研究罐体的临界倾角就转化为研究投影的静矩与惯性矩关系系数的问题。

罐体的形态不同，则投影平面的形状不同，静矩与惯性矩关系系数也不相同，因此，寻求不同平面图形的静矩与惯性矩关系系数是解决液体系统稳度问题的重要课题，但本文重点探寻平面图形静矩与惯性矩关系系数具有的基本性质，这对解决一般液体系统的稳度问题具有普适意义。

2.2 关系系数的性质

2.2.1 标度变换不变性

对于由单调连续函数y1=f1（x）、y轴、x1=a和x轴围成平面图形M1（图4），它的x轴特征长度为xmax1=a，其面积和绕y轴的静矩、惯性矩以及静矩与惯性矩关系系数分别为：

图4 中，先固定M1在x轴上的边，将M1沿y轴放大k1倍（k1>0）；再固定M1在y轴上的边，将图形沿x轴放大k2倍（k2>0），得到平面图形M2。此时M2由函数y2=f2（x）、y轴、x2=k2a和x轴围成，它的x轴特征长度为xmax2=k2xmax1=k2a，其面积和绕y轴的静矩、惯性矩以及静矩与惯性矩关系系数分别为：

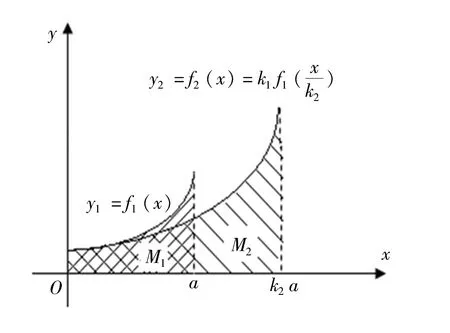
图4 标度变换不变性推证用图Fig. 4 Diagram for proof that has invariance of scale transformation

分别比较式（12）与式（16）、式（13）与式（17）、式（14）与式（18）、式（15）与式（19），可知：平面图形先后沿y轴、x轴放大k1、k2倍后，其面积变为原来的k1k2倍，绕y轴的静矩变为原来的倍、惯性矩变为原来的k1k32倍，而静矩与惯性矩关系系数保持不变。

同理可证，平面图形放大后，绕x轴的静矩与惯性矩关系系数也保持不变，即px2=px1。

物体尺度大小的变换叫做“标度变换”，标度变换过程中平面图形的静矩与惯性矩关系系数保持不变的性质，称为平面图形静矩与惯性矩关系系数的标度变换不变性。平面图形静矩与惯性矩关系系数的标度变换不变性为工程试验的小规模化提供了理论依据。利用该理论可以在实践中将大尺度液体系统的稳度问题通过缩小系统尺寸转换为小尺度问题进行研究。

2.2.2 定轴平移不变性

平面图形N1处于xOy平面内（图5），在N1上（xi，yi）处取面元dAi，则N1绕y轴的静矩与惯性矩关系系数为：

图5 定轴平移不变性推证用图Fig. 5 Diagram for proof that has invariance of translation along fixed axis

将N1沿y轴平移δ得到N2，在N2上（xi，yi+δ）处取与dAi相同的面元dAi′，则N2绕y轴的静矩与惯性矩关系系数为：

若将N1沿x轴平移任意距离，同理可证px2=px1。

式（21）表明：平面图形在其平面内沿定轴平移时，绕定轴的静矩与惯性矩关系系数保持不变。该结论称为平面图形静矩与惯性矩关系系数的定轴平移不变性。

2.2.3 第一类平面图形的垂直轴等值性

设平面图形T在第一象限内由函数y=f（x）和它的反函数x=f-1（y）组成（图6），由于函数和它的反函数关于y=x对称，从而轴y=x将T分成两个对称区域A1、A2。在A1内（xi，yi）处取面元dAi，在A2内取dAi关于y=x对称的面元dAi′，根据对称性有xi=y′i，从而xidAi=y′idA′i，x2idAi=y′i2dA′i。

图6 垂直轴等值性推证用图Fig. 6 Diagram for proof that has equivalence on plane graph

在A1区域，有

从而得到平面图形T对坐标轴的静矩、惯性矩关系，如下所示：

设平面图形T在x、y轴的特征长度分别为xmax、ymax，因为T关于轴y=x对称，有ymax=xmax。此时T对坐标轴的静矩与惯性矩关系系数满足：

式（22）表明：关于轴y=x对称的平面图形，绕相互垂直轴的静矩与惯性矩关系系数相等。这类特殊的平面图形称为第一类平面图形，该结论为平面图形静矩与惯性矩关系系数的垂直轴等值性。

进一步研究表明，还存在第二类平面图形，它们虽然并不关于轴y=x对称，但绕相互垂直轴的静矩与惯性矩关系系数也相等，这将另文阐述。

3 有质平面图形静矩与惯性矩关系系数

3.1 关系系数的定义

目前，研究平面图形静矩与惯性矩关系系数时并未考虑质量，而质量是决定液体系统稳度的重要因素。因此，从理论上探索有质物体稳度的计算方法，对解决实际工程问题具有重要指导价值。

为叙述方便，本文将考虑质量的平面图形称为有质平面图形，质量在平面内的分布状态用质量面密度描述。

设有质平面图形U处于xOy平面内（图7），在U上（x0，y0）处取面元dA，dA的质量面密度为σ（x0，y0），则U绕y轴的静矩、惯性矩（此时也称转动惯量）以及绕x轴的静矩、惯性矩分别为：

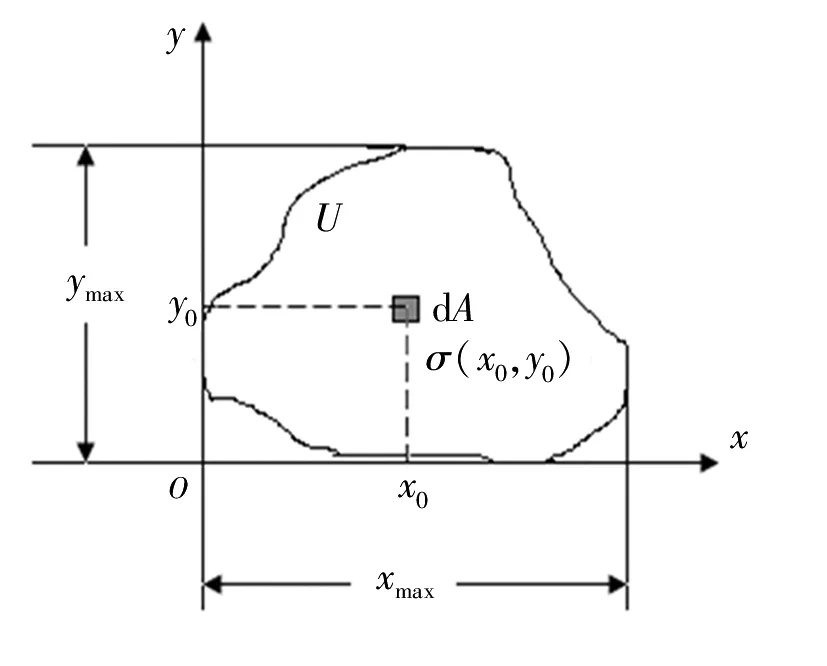
图7 有质平面图形静矩与惯性矩关系系数的定义用图Fig. 7 Diagram for definition of relation coefficient between static moment and moment of inertia with mass on plane graph

定义有质平面图形U绕y轴、x轴的静矩与惯性矩关系系数分别为：

式中：x′max、y′max分别为平面图形U在x、y轴上的特征长度，m。

3.2 标度变换时有质平面图形的静矩与惯性矩关系系数

3.2.1 轴向幂函数分布状态下的静矩与惯性矩关系系数

在xOy平面内由单调连续函数y1=f1（x）、x轴、y轴和x=a围成的有质平面图形V1（图8），其质量面密度沿x轴方向按幂函数σ（x）=λxn（λ为常量，且λ≠0）分布，而y轴方向不变，则V1对y轴的静矩、惯性矩以及静矩与惯性矩关系系数分别为：

图8 面密度呈幂函数分布的有质平面图形标度变换不变性推证用图Fig. 8 A proof diagram for scale transformation invariance of qualitative plane figure with power function distribution of areal density

图8 中，先固定V1在x轴上的边，将V1沿y轴标度变换k1倍；再固定V1在y轴上的边，将图形沿x轴标度变换k2倍，得到V2，则V2在x轴的特征长度xmax2=k2xmax1=k2a，V2对y轴的静矩、惯性矩及静矩与惯性矩关系系数分别为：

分别比较式（28）与（31）、式（29）与（32）、式（30）与（33），可知：质量面密度沿x轴按幂函数σ（x）=λxn（λ为常量，且λ≠0）分布，而y轴方向不变时，有质平面图形沿y轴标度变换k1倍、再沿x轴标度变换k2倍后，其静矩变为原来的k1kn+22倍、惯性矩变为原来的k1kn+32倍，而静矩与惯性矩关系系数保持不变。

分别比较式（13）～式（15）与式（28）～式（30）、式（17）～式（19）与式（31）～式（33），可知：（1）平面图形因考虑了质量，其静矩、惯性矩以及绕坐标轴的静矩与惯性矩关系系数一般都会发生变化；（2）尽管标度变换过程中有质平面图形的静矩与惯性矩关系系数保持不变，但该系数与不考虑质量时的值一般不同。

考虑特殊情形，若令n=0（x≠0），则σ（x）=λ，即质量面密度沿x轴为常值λ，此时平面图形V1对y轴的静矩、惯性矩以及静矩与惯性矩关系系数分别为：

标度变换后平面图形V2对y轴的静矩、惯性矩以及静矩与惯性矩关系系数分别为：

分别比较式（13）与（34）、式（17）与（37）以及式（14）与（35）、式（18）与（38），可知：质量面密度沿x轴（x≠0）为常数λ而y轴方向不变时，有质平面图形的静矩和惯性矩总是不考虑质量时的λ倍，与是否进行标度变换及变换比例无关。这说明质量分布对平面图形的静矩和惯性矩有着重要影响。

比较式（13）与（17）、式（34）与（37）以及式（14）与（18）、式（35）与（38），可知：质量面密度沿x轴（x

≠ 0）为常数λ，而y轴方向不变时，将图形沿y轴标度变换k1倍、再沿x轴标度变换k2倍后，其静矩变为原来的倍、惯性矩变为原来的倍。这说明标度变换过程中有质平面图形静矩和惯性矩的变化比例与质量面密度λ无关，但受制于变换比例k1、k2。

比较式（30）与式（33）、式（36）与式（39），可知：质量面密度相等时，有质平面图形的静矩与惯性矩关系系数在标度变换过程中始终保持不变，与是否考虑质量无关。

3.2.2 质量保持不变时的静矩与惯性矩关系系数

在xOy平面内由单调连续函数y1=f1（x）、x轴和x=a、y轴围成的有质平面图形W1（图9），其质量面密度均匀分布且为σ1，则平面图形W1的面积和绕y轴的静矩、惯性矩以及静矩与惯性矩关系系数分别为：

图9 中，将W1沿y轴标度变换k1倍，再沿x轴标度变换k2倍后，得到W2，则W2的面积为：

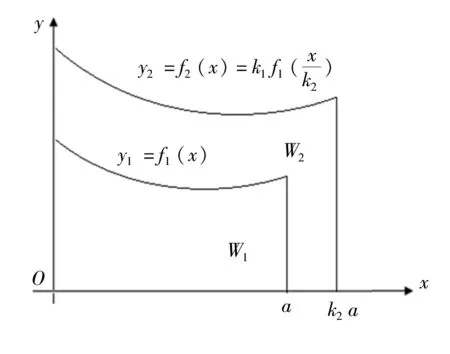
图9 质量保持不变的有质平面图形标度变换不变性推证用图Fig. 9 A proof diagram for scale transformation invariance of qualitative plane figure with constant quality

设W2的质量面密度也均匀，且为σ2，由于标度变换过程中质量保持不变，即质量m=σ1A1=σ2A2，所以σ1与σ2间存在如下关系。

W2对y轴的静矩、惯性矩以及静矩与惯性矩关系系数分别为：

式（41）～式（48）表明：在质量保持不变时，有质平面图形沿y轴标度变换k1倍、再沿x轴标度变换k2倍后，其质量面密度会发生变化，绕y轴的静矩、惯性矩也会变化，但静矩与惯性矩关系系数保持不变，并且与不考虑质量时相同。

以上研究表明：对于有质平面图形，只要质量面密度处处相等，无论是否进行标度变换，它的静矩与惯性矩关系系数总保持不变，且与不考虑质量时相同。

4 结语

本文在模型假设的基础上推导出罐体临界倾角的表达式，将液体系统稳度的立体问题转化为平面问题，进而转化为平面图形的静矩与惯性矩关系系数的问题。研究发现，对于平面图形，只要质量面密度处处相等，无论是否进行标度变换，它的静矩与惯性矩关系系数总保持不变，且与不考虑质量时相同。该结论对于研究工程中液体系统的稳度问题具有理论指导意义。