思维之道：数学教学的着力点

李昌官

(浙江省台州市教育局教研室 318000)

虽然人们普遍认为数学是思维的体操，但数学作为“思维体操”的功能并没有得到充分利用．这主要缘于数学教学存在如下三方面的缺陷：一是重知识技能而轻数学思维；二是重思维结果而轻思维过程；三是思维指导不到位、不给力，学生思维难以“开窍”．

1 何为思维之道

思维有“道”，这是毫无疑问的．这里的“思维之道”，一是指思维的原理与规律；二是指思维的缘由与依据；三是指思维的策略与方法；四是指思维的路径与节点．

2 为何要强化思维之道教学

苏霍姆林斯基(В.А.Сухомлинский，1918-1970)指出：“如果一个人在童年时期还能胜任脑力劳动并且从中感到乐趣，而到了少年时期，学习对他来说却变成了痛苦的负担，那么这正是由于没有借助抽象思维发展他的头脑所造成的可悲后果．儿童的智力才能到了少年时期好像在慢慢黯淡下来和趋向迟钝，这是十分令人担忧的．”[1]杜威(John Dewey，1859-1952)也指出：“思维需要细心而周到的教育的指导，才能充分地实现其机能．不仅如此，思维还可能沿着错误的途径，导引出虚假的和有害的信念．思维系统的训练之所以必要，不仅在于担心思维有缺乏发展的危险，更为重要的是担心思维的错误的发展．”“学习就是要学会思维”，“教育在理智方面的任务是形成清醒的、细心的、透彻的思维习惯．”[2]数学思维之道是学生学会学习数学、学会思考、学会创造的关键；教好数学的关键在于“示以学生思维之道”[3]；揭示思维之道、强化思维之道教学是发展学生思维最根本的途径与方式．

3 如何强化思维之道教学

3.1 揭示思维的原理与规律

思维是有规律的，认识和把握思维的一般规律对数学学习至关重要．先宏观后微观、先直觉后逻辑、先定性后定量、先特殊后一般、先形后数、先残缺后全面、先合情推理后演绎推理、先归纳事实后建构理论体系，等等，都是十分常用而一般的数学思维规律．以“先宏观后微观”为例，无论是对几何体的认识，还是对人或其他事物的认识，人们通常都是先有一个总体的、大致的认识，再在总体的“指引”下深入地认识各个局部．正如克伯屈(William Hurd Cobbler，1871—1965)所说：“人们不是先得到爪子、腿、躯体、尾巴和头的各自概念，然后拼凑起来形成狗的概念一样，而是相反．”[4]因为在认识一个新的事物之初，“如果你深入到细节中去，你就可能在细节中迷失自我．过多过细的枝节对思维是一种负担．它们会阻碍你对要点投入足够的注意力，甚至会使你全然看不到要点．”[5]

案例1平面向量的基本定理教学

平面向量的基本定理教学需要经历提出问题、猜想结论、完善结论、证明结论、运用定理的过程．教学时，让学生认识到同一平面内的向量(如图1)是充满联系的，然后再探究这种联系，是先宏观后微观．受力的分解启发，猜测一个向量可以用不共线的两个向量来表示(如图1、图2)，然后基于向量的平行四边形法则得到图3，是先直觉后逻辑．在确认任一个向量a可用两个不共线的向量e1,e2来表示的基础上，找出具体的量λ1,λ2，把它们的关系表示为a=λ1e1+λ2e2，是先定性后定量．通过观察图3得到a=λ1e1+λ2e2，是先形后数．发现只考虑图1或图2的情形是不完善的，还应考虑a是与e1或e2共线的非零向量以及a是零向量两种情形，是从残缺到全面．从平面向量的基本定理到向量的正交分解和坐标表示，再到向量运算的坐标表示，是从归纳事实到构建理论体系．

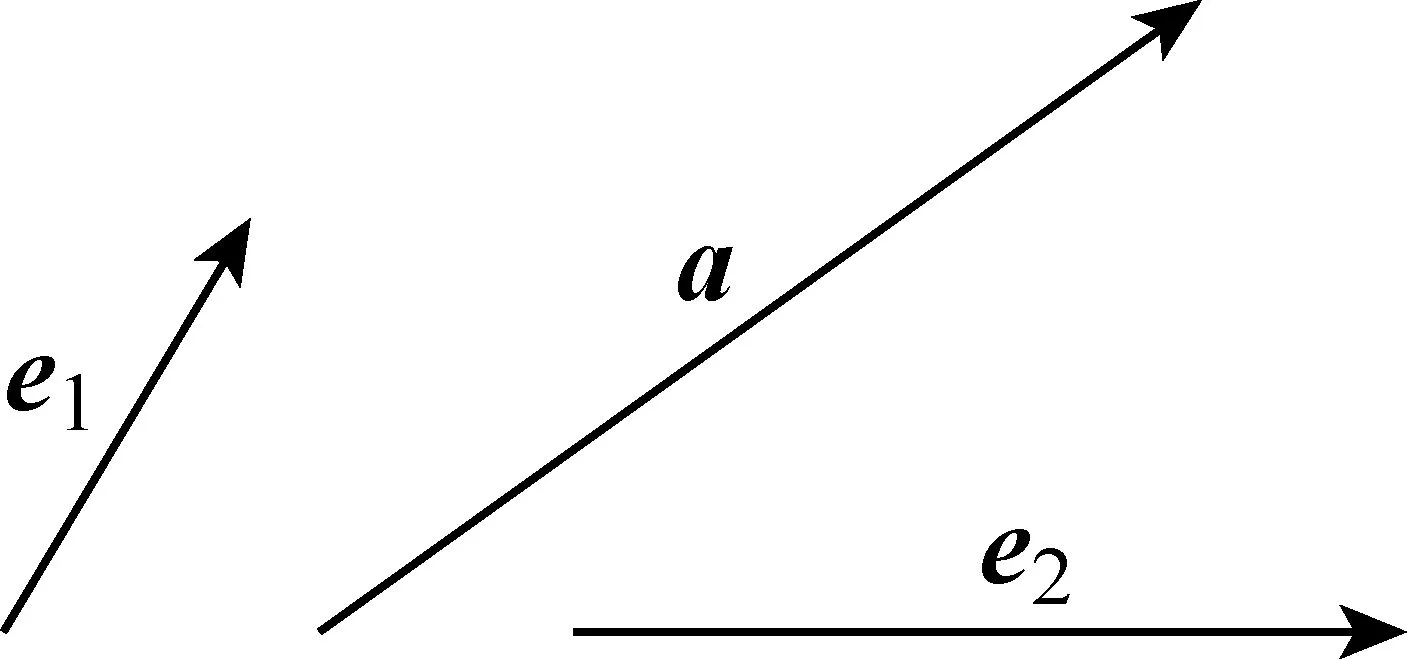
图1

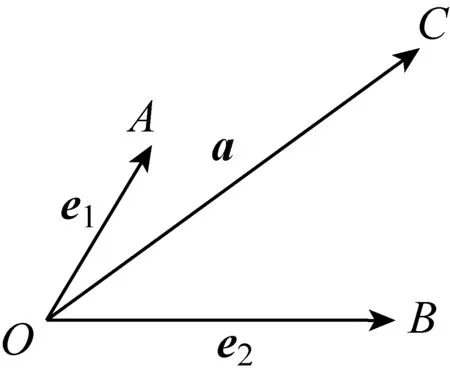
图2

图3

数学教学应通过具体事例，不断地揭示思维的基本规律，深化学生对思维的基本规律的认识，进而自觉地、主动地运用思维的基本规律思考、解决问题．

3.2 揭示思维的缘由与依据

学生在问题解决中面临的最大问题与困难往往是不会想、想不到，因此指导和帮助学生会想、能想到是教师工作的核心任务，而揭示思维的缘由与依据是指导和促进学生会想、能想到的最重要的途径与方式．因为思维的中心因素是“一种事物指示或预示另外一种事物，这种功能引导我们去思考一种事物在多大程度上可以看做另一事物的根据”[6]．数学教学应揭示思维的缘由与依据，帮助学生搞清楚一事物是怎样指示或预示另一事物的，从而促进学生“形成重论据、有条理、合乎逻辑的思维品质和理性精神”[7]．

案例2已知点A，B是抛物线y2=4x上2个不同的点，O为原点，且OA⊥OB.

(Ⅰ)求证：直线AB过定点；

(Ⅱ)求点O到直线AB距离的最大值.

为了凸显一个事物如何指示或预示另一个事物，作如下分析：

(1)问题的目标预示着思维的目标与方向，因此我们应围绕证明直线AB过定点展开思考．

(2)从问题的情境看，这是解析几何问题，因此宜用坐标法求解，即应通过建立直线AB的方程来证明直线AB过定点．

(3)由于过定点的直线的方程含有1个参数，因此需要导出只含1个参数的直线AB的方程．

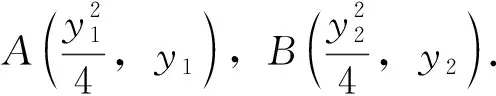
(6)由于有(Ⅰ)的结论作为基础，由“垂线段最短”知，问题(Ⅱ)中的最大值即为原点O到直线上的定点的距离．

(7)如果没有问题(Ⅰ)作铺垫，问题(Ⅱ)可视为以解析几何为背景的函数问题．由于高中所学的函数都是单变量函数，因此直线AB的方程宜含1个参数．利用点到直线的距离公式，可把点O到直线AB的距离用这个参数的表达式来表示，进而求出距离的最大值．

问题解决思路、方法的寻找与探究往往依赖经验和直觉．我们应努力追寻事物之间的联系，追寻一个事物指示或预示另一事物的因素，追寻直觉背后的逻辑和引领逻辑的直觉[8]，从而使自己的思维更好地建立在证据和逻辑的基础上．

3.3 揭示思维的策略与方法

“工欲善其事，必先利其器．”数学思维策略与方法就是数学思维与问题解决的“器”．数学思维的策略与方法有很多，如，从数学概念的定义入手、从条件与结论之间的差异入手、从事物产生的源头入手、从事物的构成要素入手、从问题中的关键因素入手、以退求进、以简驭繁、正难则反、特殊化与一般化、映射化归，等等．

案例3一组多变量问题

(1)(2018年高考数学江苏卷第13题)在△ABC中，角A，B，C所对应的边分别为a，b，c，∠ABC=120°，∠ABC的平分线交AC于点D，且BD=1，则4a+c的最小值为________.

(2)(2018年高考理科数学北京卷第7题)在平面直角坐标系中，记d为点P(cosθ，sinθ)到直线x-my-2=0的距离，当θ，m变化时，d的最大值为

(A)1 (B)2 (C)3 (D)4

(3)(2018年高考数学江苏卷第14题)已知集合A={x|x=2n-1，n∈N*}，B={x|x=2n，n∈N*}，将A∪B的所有元素从小到大依次排列构成一个数列{an}，记Sn为数列的前n项和，则使得Sn>12an+1成立的n的最小值为________.

(4)(2013年高考理科数学全国Ⅱ卷第21题)已知函数f(x)=ex-ln(x+m).

(Ⅰ)设x=0是f(x)的极值点，求m，并讨论f(x)的单调性；

(Ⅱ)当m≤2时，证明f(x)>0．

(Ⅰ)讨论f(x)的单调性；

思维策略与方法教学的关键在于把握其实质与灵魂，结合具体事例把它们用活、用好，进而运用它们解决更多、更一般的问题．

3.4 揭示思维的路径与节点

“凡事预则立，不预则废．”当下数学教学和问题解决“走一步算一步”、缺乏整体规则和安排的现象比较严重，这不仅造成了学生的学习只能跟着教师亦步亦趋，而且也不利于他们思维的发展．就单元教学而言，应突出和强化思维和问题解决的基本路径教学，揭示数学发展的基本线索与基本步骤．如，研究集合、向量、概率、复数等可运算的数学对象的基本路径通常是现实背景—运算对象—对象间的关系—运算法则—运算律—应用；研究几何对象的基本路径通常是背景—概念—表征—性质—判定—应用—推广．

案例4集合教学

高中集合教学主要包括三方面的内容：集合的概念、集合的基本关系、集合的基本运算．提出研究集合问题、建构集合概念时，就应意识到这不仅是为了刻画具有某种“类”的性质的全体，也是为了从数学角度研究它们，或者说对它们进行运算．建构集合概念时，应意识到集合元素的“确定性、互异性、无序性”是为确定集合间的关系、对集合进行运算服务的．没有集合元素的确定性，判定集合间的关系、进行集合运算就无从谈起；没有集合元素的互异性与无序性，集合的表示方式、集合之间的关系、集合的运算法则将发生极不合理的变化，甚至无从谈起．反之，集合运算是集合的概念、集合间的基本关系逻辑发展的必然；没有集合运算，前面这些研究将失去其最重要的意义与价值．

数学教学不仅应让学生了解数学知识发展的基本路径、基本环节，还应让他们感受和体会知识发展的内在逻辑以及各环节的相互联系、相互影响等；应通过具体事例让学生在真实的情境中体会和认识到：思维应“不止于观念的‘连续’(sequence)，而要求它连续的结果(consequence)——它是一个持续的、有步骤的过程．前一步决定后一步的结果，后一步参照前一步的成因；一步一步，相因而发生，相辅而成立……各个单位，这样互相连贯，持续地向着一个共同的目的前进．”[9]

就数学解题而言，应尽量在具体操作之前搞清楚解题的主导思想，做到“三思而后行”，而不是像“玻璃罩里的苍蝇盲目乱撞”．我们应牢记波利亚的教诲：数学也许往往像是猜想游戏，在你证明一个定理之前，你必须猜想到这个定理，在你搞清楚证明细节之前，你必须先猜想出证明的主导思想．[10]事实上，前面的案例2、案例3就是在猜想解题的主导思想、搞清楚解题的基本思路与方法．

3.5 示范真实的思维过程

“在我们教给学生更传统、更正式的演绎和证明的方式之前，培养他们对材料的直觉理解才是首要任务．”“如果学生从来没有见过他们的长辈们有效地使用直觉思维，那么他们几乎不可能或没有信心来培养自己的直觉思维．对于学生提出的问题，那些愿意猜测答案然后让学生来批判分析的教师，比预先为学生分析好一切的教师更容易培养学生的直觉思维习惯．”[11]因此教师展示自己真实的思维过程，谈自己看到题目时的第一感觉或直观感觉，示范面对思维障碍时如何突破、拐弯，对学生来说非常重要．

案例5已知E，F分别是四面体的棱AB，CD的中点，过EF的平面与棱AD，BC分别相交于G，H，则

障碍一及其突破：对于GH与EF的关系，也许我们开始时局限于平面PEF内思考而一无所获．由E，F分别是四面体的棱AB，CD的中点，觉察、猜测思维的突破方向是把平面问题转化为空间问题来解决．分别取AC，BD的中点M，N(如图4)，不难发现四边形EMFN是平行四边形，AD∥平面EMFN，BC∥平面EMFN，且AD，BC到平面EMFN的距离相等．又EF与GH的交点O既在平面EMFN与平面PEF的交线EF上，也在平面AHD与平面EMFN的交线GH上，故OG=OH，EF平分GH．

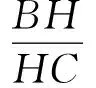
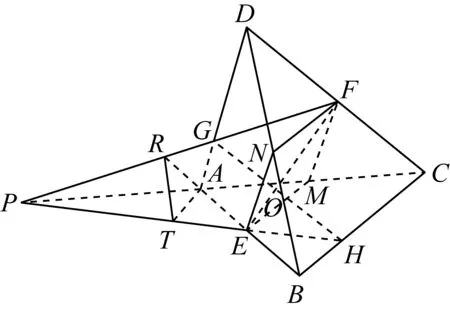
图4

4 结束语

为什么而教既关乎数学教学的目标与方向，也关乎数学教学的策略与方法．数学教学应通过强化思维之道教学，达到两方面的目的：一是有效地解决眼前面临的问题，避免无效探究；二是以解决眼前的问题为载体，学习和掌握思维之道，提升学生的数学学科核心素养．