一道高考题的解法探索与思考
——极值点偏移的七种证明方法
2022-03-05 09:20甘肃省张掖市第二中学734000彭万坤白燕茹
中学数学研究(江西) 2022年3期
甘肃省张掖市第二中学 (734000) 彭万坤 白燕茹
导数常做为高考压轴题,大多数学生由于理解不透彻、感觉比较难,从而放弃不做.俗话说:“学之道在与思、思之果在于悟”.通过对解题过程进行自觉的总结反思、归纳,不仅对解题方法有了较全面的认知,还可以在理解常规解题模型的基础上进行深层探究,从而诱发新的思考并提炼新的方法.
试题已知函数f(x)=lnx-ax.(1)讨论函数f(x)的单调性;(2)若函数f(x)有两个不同的零点x1、x2,证明:x1x2>e2.
第一问解法省略,下面仅对第二问的证明方法进行分析.

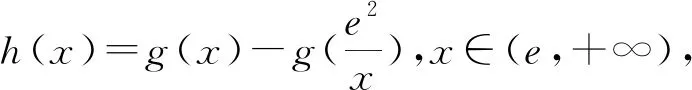

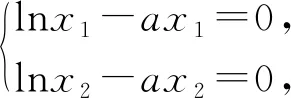
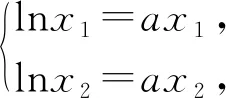

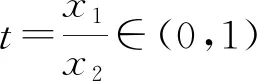


在数学解题教学中,同一个数学问题存在不同的解题思路,即一题多解,教会学生站在不同的角度去思考、审视、反思、总结,进而开阔自己的解题思路.

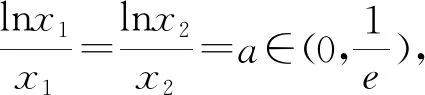
俗话说:“学而不思则罔,思而不学则殆”.只有通过这样的感悟,归纳提炼,反思总结,不仅能让学生领悟探究数学解题的愉悦感,而且也能有效激发数学思维方法,促进数学素养的不断提高.
猜你喜欢
南方医科大学学报(2021年10期)2021-11-10
小学生学习指导(低年级)(2021年3期)2021-07-21
新世纪智能(数学备考)(2021年11期)2021-03-08
小学生学习指导(低年级)(2018年3期)2018-01-31
都市家教·上半月(2017年7期)2017-08-15
三联生活周刊(2016年23期)2016-06-08
新高考·高一数学(2016年3期)2016-05-19
少儿科学周刊·少年版(2015年1期)2015-07-07
中学课程辅导·教师通讯(2014年9期)2014-09-17
小说月刊(2014年1期)2014-04-23

