基于时序差分学习的强化学习算法实验教学案例设计

邱煜炎，高心乐，吴福生

（1.蚌埠医学院 卫生管理学院，安徽 蚌埠 233000；2.蚌埠医学院 图书馆，安徽 蚌埠 233000）

人工智能对社会和经济的影响日益凸显，各国政府先后出台了发展人工智能的政策，并将其上升到国家战略的高度[1]。机器学习是解决当前众多人工智能问题的核心技术，常用的机器学习算法主要分为有监督学习、无监督学习、半监督学习和强化学习四大类[2]。国内相关高等院校开设了机器学习算法课程，课程结构涵盖原理与推导、工程实现和应用三个方面[3]。但受限于强大的算力需求、复杂的数学公式以及零星的项目实例，国内高校介绍强化学习算法仅停留在理论讲授层面，未将其落地实践，这不利于学生对算法的通透理解。

强化学习是机器学习的一个重要分支，主要研究如何在环境中做出合适的动作以获得最大化奖励[4-7]，其涉及智能体（Agent）、环境（Environment）、动作（Action）和奖励（Reward）这几个核心概念。智能体存在于环境中，并根据环境执行动作获得一定奖励。奖励有正有负，强化学习的目标就是自主构建一个策略，使得智能体针对不同状态合理化作出相应反馈，以此争取最大的分值回报[8]。围棋程序Alpha‐Go及其升级版本AlphaZero的核心算法就是强化学习[5]。

强化学习算法通过样本学习得到一个映射函数π，其输入是当前时刻环境信息，输出是要执行的动作：a=π(s)，其中，s为状态，a为要执行的动作，执行动作的目标是要达到某种目的。在强化学习中用回报函数对此进行建模，针对模型是否已知构建不同的强化学习算法。对于现实世界任务，环境的转移概率、反馈的奖赏函数往往很难确知，因此，针对模型未知的强化学习算法才具有普适意义。其中，SARSA算法和Q学习作为模型未知的基础算法，具备清晰的推导流程、明确的算法步骤、低廉的算力要求和广泛的应用场景，因此，本文采用SARSA算法和Q学习，设计了“时序差分学习的强化学习算法”实验教学项目案例，以降低强化学习课程的导入门槛，帮助学生掌握强化学习算法的设计精髓及程序框架，熟悉策略迭代的几种优化方式，

1 算法原理

SARSA算法和Q学习同属于时序差分算法（Temporal Difference Learning）类目[9]，具有相似的算法流程，都是在智能体反馈行动过程中迭代式地学习Q函数，但二者采取了不同的迭代策略。

1.1 时序差分算法

SARSA算法和Q学习均采用了时序差分算法的设计理念[10]，即执行一个动作之后就进行价值函数估计，直接通过生成的随机样本进行计算。因此，二者具备无须计算完整片段、无须依赖状态转移概率的特点。最基本的时序差分算法是利用贝尔曼方程估计价值函数的值，然后再构造更新项。迭代更新公式为

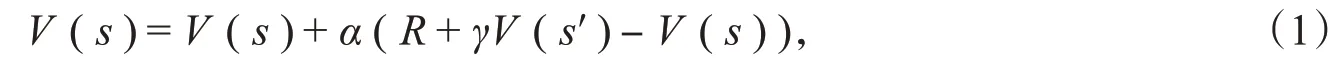
其中，R为当前动作的立即回报值，α为人工设置的学习率，γ为衰减系数，V(s′)为下一时刻状态价值函数[11]。该算法采用当前动作的立即回报值与下一状态当前的状态价值函数估计值之和构造更新项，并更新状态的价值函数，更新项为R+γV(s′)。

1.2 SARSA算法

SARSA算法用于估计给定策略的动作价值函数，同样采用每次执行一个动作就进行更新的方式。其迭代更新公式为

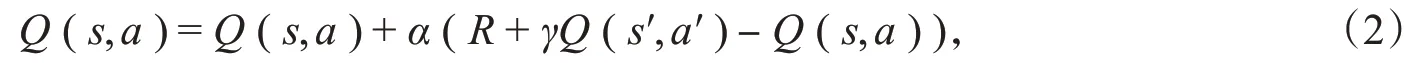
其中，Q(s,a)代表动作价值函数[12]，其他参数意义同式（1）。SARSA算法实施时需要根据当前动作价值函数的估计值为每个状态选择一个动作来执行，采用探索（Exploration）和利用（Exploitation）相结合的方式进行选择，即ε-贪心策略。以1-ε的概率执行最优动作，以ε的概率随机选择其他动作。执行完动作之后，进入状态，然后寻找状态下所有动作的价值函数的极大值、构造更新项。该算法最终收敛到动作价值函数的最优值，其算法流程如下。

（1）初始化。将所有非终止状态的Q(s,a)初始化为任意值，终止状态的初始化为0。

（2）外循环运行经验轨迹。对于所有片段，随机选择一个初始状态s，根据Q函数为状态s采用ε-贪心策略选择一个动作a。

（3）内循环运行经验轨迹中的时间步。执行动作a，得到立即回报R以及下一个状态s′，再根据Q函数为状态s′采用ε-贪心策略确定一个动作a′，根据公式（3）更新Q函数，更新状态s=s′和动作a=a′。

（4）重复步骤（3）直到s确定为终止状态。

（5）重复步骤（2）直到所有经验轨迹执行结束，输出最终动作值函数Q(s,a)。

1.3 Q学习

Q学习与SARSA算法的区别在于后者是一种同策略算法，选择动作时的策略与更新动作值函数时的策略相同，Q学习则是异策略算法，在选择动作时所遵循的策略与更新动作值函数时策略不同，其迭代公式为

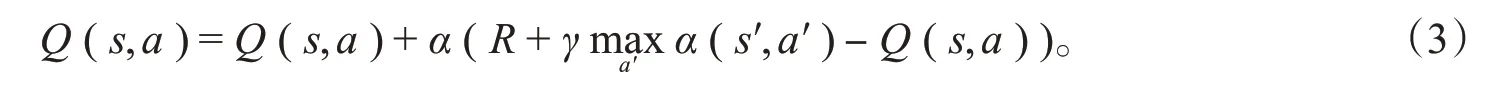
式（3）与式（2）的区别在于Q学习估计动作价值函数最大值，通过迭代运算可以找到价值函数的极值，从而确定最优策略。

与SARSA算法类似，Q学习也采用ε-贪心策略为每个状态选择动作，其算法流程如下。

（1）初始化。将所有非终止状态的Q(s,a)初始化为任意值，终止状态的初始化为0。

（2）外循环运行经验轨迹。对于所有片段，随机选择一个初始状态s，根据Q函数为状态s采用ε-贪心策略选择一个动作a。

（3）内循环运行经验轨迹中的时间步。执行动作a，得到立即回报R以及下一个状态s′，再根据Q函数为状态s′采用ε-贪心策略确定一个动作a′，根据公式（4）更新Q函数，更新状态s=s′。

（4）重复步骤（3）直到s确定为终止状态。

（5）重复步骤（2）直到所有经验轨迹执行结束，输出最终动作值函数Q(s,a)。

1.4 算法对比

综上所述，SARSA算法与Q学习具备大致相同的算法流程，都采用双循环迭代优化运算的方式，区别在于选择动作时所遵循的策略与更新动作值函数时所用的策略不同[13-15]，详见表1。

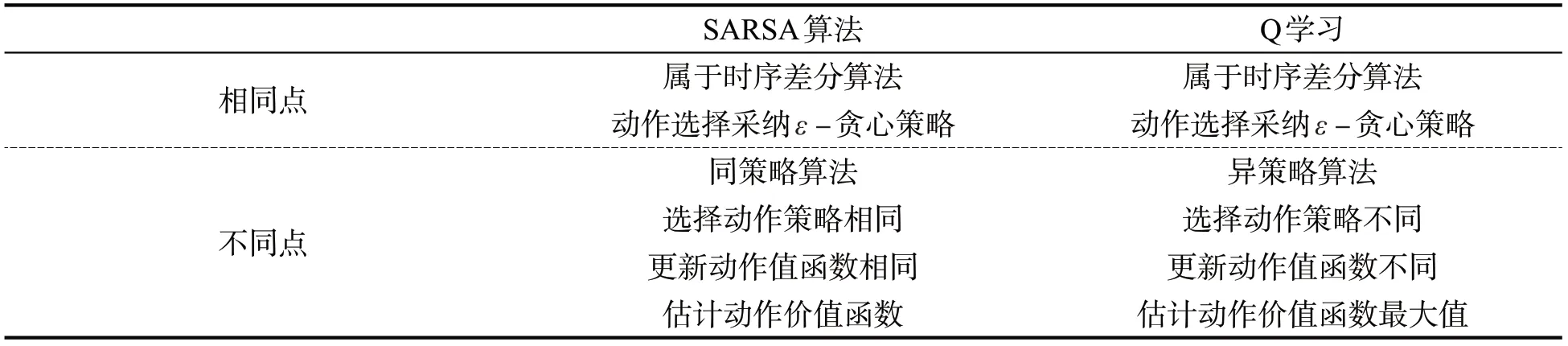
表1 SARSA算法与Q学习对比

2 实验设计

鉴于二者一致的算法流程，笔者在设计实验时采用相同的运算框架。本实验拟在确定的网格内解决“走迷宫”问题。

2.1 定义环境

本文以二维点阵的形式绘制迷宫地图，通过初始化参数设定地图的长宽大小，如图1所示。A表示智能体，它一共有4个动作：上移、下移、左移、右移[16]；实心点号“.”表示迷宫的边缘，智能体只能在边缘内移动，不能越界；“O”表示一个宝藏，当智能体移动到宝藏位置，即判定找到宝藏，并获得相应奖励；此外，“X”代表可选择的陷阱图标，也可根据需要定义陷阱的数量以提高游戏的难度，当智能体移动至该位置，所得奖励分为负值。

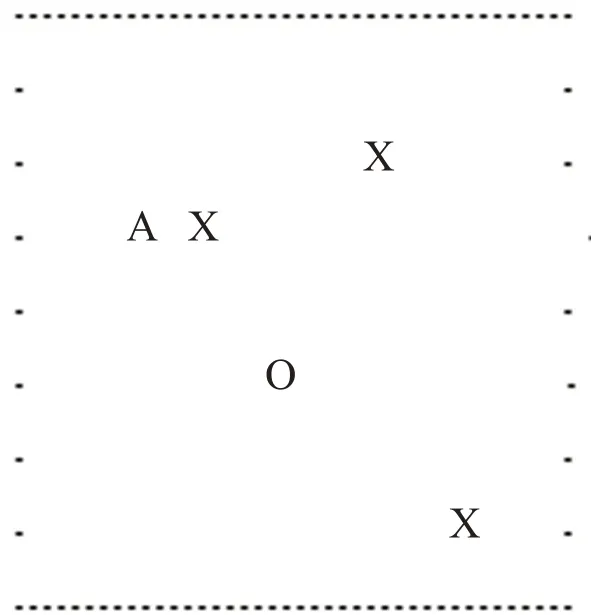
图1 “走迷宫”地图

2.2 明确关系

结合以上定义的游戏环境，明确强化学习算法的核心概念和游戏应用的对应关系。其中，智能体可以在边界内自由移动，环境以整个迷宫为代表，动作指代智能体上、下、左、右四种可采取行为，状态代表智能体在迷宫中的位置，以二维坐标表示。奖励是智能体在当前状态下所得的分值。当移动至空白位置，奖励为0；当移动至宝藏处，奖励为100；当移动至陷阱处，奖励初始值-5。此外，奖励分值可以根据实验要求自由设定。

2.3 程序实现

本项目利用Python语言构建环境模块、算法模块和监控模块。环境模块作为两种算法的公用模块实现了如下主要功能：创建地图并设置地图大小、初始化智能体和宝藏位置、定义陷阱数量；此外还需要设定其他参数，例如行动的表示方法、奖励或惩罚的分值以及迷宫的终止状态。算法模块主要通过程序语言实现SARSA和Q学习两种算法。由于走迷宫属于有限的状态和动作的集合，因此两种算法可以共同定义一张二维数组，将动作价值函数存储其中，行和列分别代表状态和动作，数组中的每一个元素即为某种状态下执行某种动作的价值函数值，见表2。

表2 Q(s,a)函数表

程序语言依据1.2节和1.3节提供的算法流程进行代码实现，并分别命名保存（sarsa.py和q_learning.py）以方便学者调试编译。程序通过外层循环参数设定游戏次数，通过内层循环参数设定智能体每次探索步数。算法运行时迭代更新数组元素，直至收敛。

3 实验结果与分析

本项目运行环境为操作系统Ubuntu14.04、编程语言Python2.7和IDE编译环境PyCharm2018。由于算法程序不断刷新输出，不适合观察，为方便实验者追踪智能体行动轨迹并提供与算法程序一致的重印程序，选择reprint库替代print函数以方便观测结果。根据地图大小、陷阱数量设置了不同的环境，并对比观测了SARSA算法与Q学习的性能，具体参数见表3。

表3 实验参数设置

3.1 总体描述

参照表3，一共执行了6次对比实验，每次实验通过若干指标进行性能对比，结果见表4。可以看出：当无障碍物时（实验1和实验4），SARSA算法表现要优于Q学习算法，并且随着地图的扩大以及迭代次数的增多，两算法整体性能越来越好，这说明智能体能充分利用大量强化学习的知识并进行移动，以获取更高分值；当地图出现障碍物时，Q学习算法要明显优于SARSA算法，甚至当负奖励分的绝对值提高时（实验3和实验6），利用SARSA算法的智能体甚至出现了负值，而且通过迭代数据细节可以发现，当SARSA算法在刚开始阶段一直处于负奖励结果时，后阶段得分一直趋于零分，这说明SARSA算法没有很强的健壮性。Q学习算法比较激进，当面对负收益时会采取积极的探索策略，因此，虽然分数低于无障碍状态，但是每次实验随着迭代的进行，最后均能保持高分奖励，详见图2。

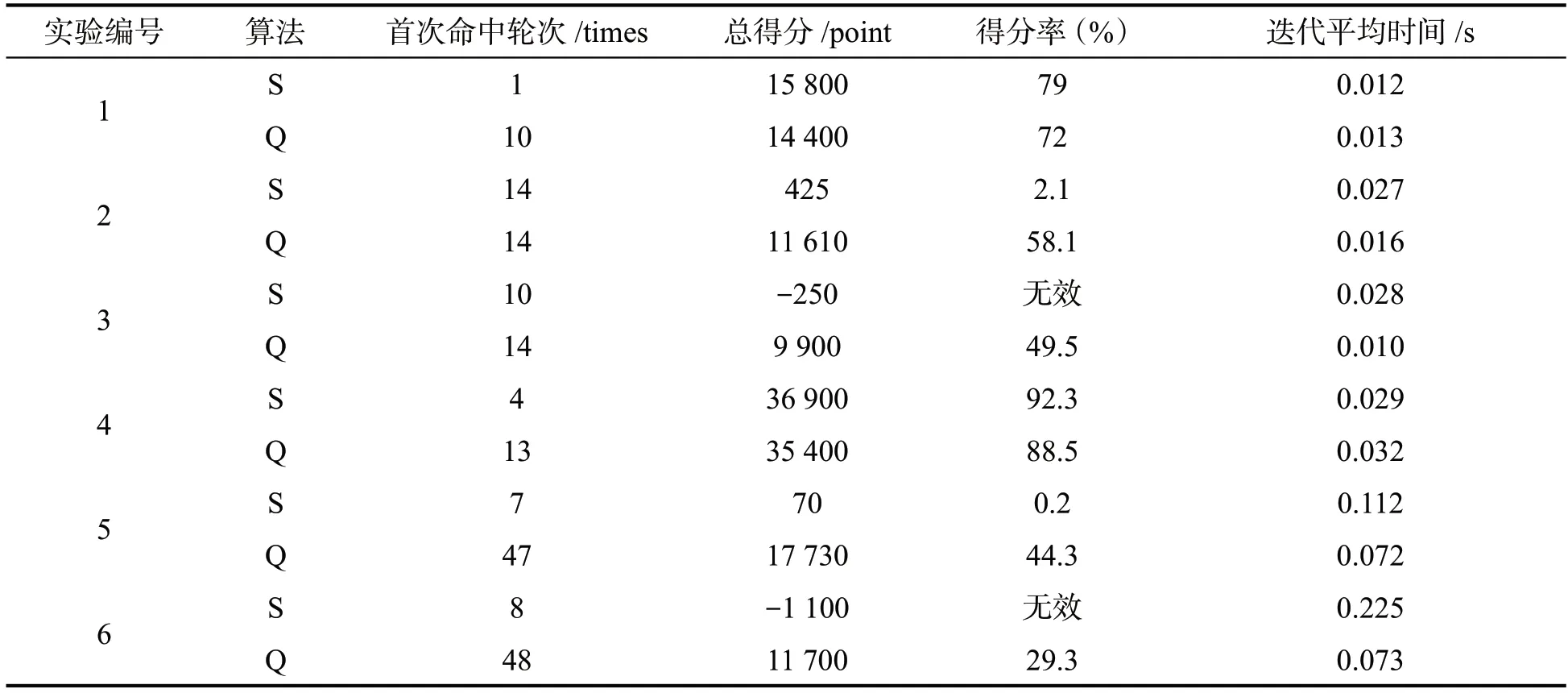
表4 6次实验指标对比（S：SARSA,Q：Q-Learning）

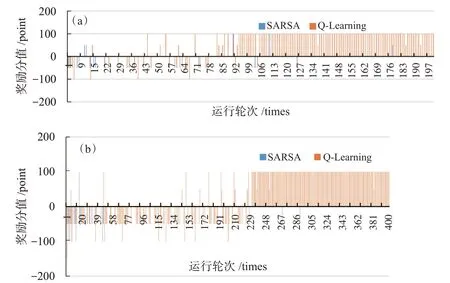
图2 两算法得分对比。（a）实验3；（b）实验6

3.2 探索效率

通过表4第3行对比数据可以看出，SARSA算法首次命中轮次基本早于Q学习算法，这说明SARSA算法在迭代初始阶段的多样性高于Q学习算法。通过监测无障碍实验环境中智能体每次的行动步数（实验1和实验4），可以判定两算法的探索效率，见下页图3。

如图3所示，SARSA算法在初始阶段表现出较频繁的多样性探索策略，随着迭代次数的增加，两种算法收敛到较低的探索步数，最后都能以快速的方式发现宝藏。同时，在没有障碍前提下，SARSA算法能略早收敛于最优解。

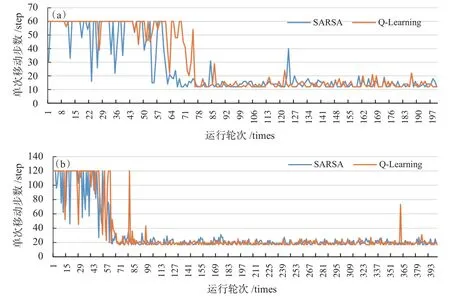
图3 两算法迭代步数对比。（a）实验1；（b）实验4

3.3 迭代时间

由表4第6行可知，在无障碍环境下SARSA算法运行时间略低于Q学习算法，而在有障碍环境下Q学习算法优势明显，下页图4追踪了4次实验（实验1、2、4、5）的每轮迭代运算时间。

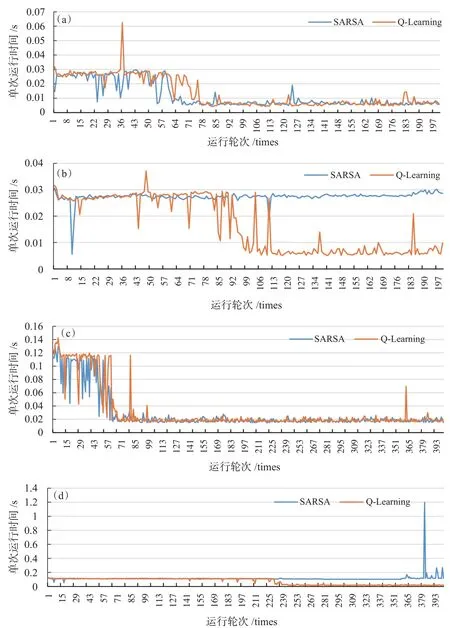
图4 每次迭代运算时间。（a）实验1；（b）实验2；（c）实验4；（d）实验5

通过跟踪4次实验的迭代运算时间可以发现，在无障碍物环境下（实验1、实验4），两种算法随着迭代次数的增加，时间逐渐收敛到低点；当环境存在障碍物时（实验2、实验5），SARSA算法一直保持高位的迭代时间，而Q学习算法的后阶段迭代时间平稳降低，性能保持较高的稳定性。综上所述，对于无障碍环境，SARSA算法的效率略高于Q学习算法；当面对障碍环境时，智能体采用Q学习算法结果优势明显，整体表现优于SARSA算法，这说明异策略时序差分的强化学习算法具有较强的鲁棒性。

4 结束语

综上所述，通过设计“时序差分学习的强化学习算法”实验教学案例，对比分析两种强化学习基本算法的原理，帮助学生掌握算法的精髓以及在不同环境下的性能优势。由于算法应用场景属于有限状态环境，因此不需要过高的计算机算力，可以在本地计算机流畅运行，适用于初学者。当然，该实验还存在诸多改进之处，譬如每次执行迭代运算之前，可随机设置智能体位置而固定宝藏位置，这样充分利用Q函数进行优化探索，以使算法具备更高的鲁棒性；也可以改进智能体多宝藏探索策略，提高算法的多样性。在未来算法实验中，亦可采纳本项目的对比测评方式设计机器学习其他基础算法，例如蒙特卡洛马尔可夫模型，也可以设计复杂的深度强化学习实践模型DQN、Actor-Critic算法等，循序渐进、以降低强化学习的教学门槛。