一类具有混合时滞的分数阶神经网络的有限时间同步分析

程景顺，张玮玮，张红梅，张 海

（安庆师范大学 数理学院，安徽 安庆 246133）

分数阶微积分本质上是任意阶的微积分，它是整数阶微积分的推广，在工程学[1]、生物学[2]、经济学[3]以及物理学[4]等领域都有广泛应用。分数阶微积分比整数阶微积分具有更多的自由度和更好的记忆与遗传性质，可以更好地描述神经元之间的信号传递关系，更精准地描述各类系统的动力学行为。

人工神经网络具有人脑的一些基本功能，其模型在不同程度、不同层次上能模拟人脑神经系统的结构。利用常微分方程刻画神经元动力学是很不准确的，因为它是局部的，无法描述神经元的记忆和遗传的性质。而分数阶微积分模型可以更准确地描述实际系统的动态响应，提高动态系统的设计和控制能力。近年来，一些专家、学者将分数阶导数引入到神经网络中，建立了分数阶神经元微分方程模型。研究表明，分数阶微积分的引入有利于神经元之间的信息传输[5]，在分数阶层次上的神经网络逼近与整数阶模型相比具有较高的收敛速度[6]，因此对分数阶神经网络的研究具有重大意义。

同步在密码学[7]、安全通信[8]、图像加密[9]等领域应用广泛，且类型很多，如准一致同步[10]、投影同步[11]、完全同步[12]、Mittag-Leffler同步[13]、全局渐近同步[14]等。在工程应用中，人们希望同步能够尽快地实现，甚至在一段有限时间内实现，基于此，有限时间同步的概念被提出。有限时间同步的概念主要有两种：（1）当t到达有限时间T时，同步误差e(t)收敛于0，当t≥T时，e(t)=0；（2）同步误差e(t)在有限时间内保持在一定的范围。本文采用第2种有限时间同步的定义。

分数阶微积分经常被用来描述记忆效应，而时滞动力学系统可以讨论另一种记忆效应。事实上，由于神经元之间的信息传输速度和信号处理受到限制，神经网络不可避免地会遇到时间延迟，这会导致系统的振荡、分叉和混沌。延迟有不同的类型，例如离散延迟[15]、泄露延迟[16]、分布式延迟[17]等。由于各种原因，时间延迟在神经网络的同步实现中不可避免。因此，对神经网络时间延迟的研究具有非常重要意义[18]。然而，对分数阶混合时滞神经网络模型的有限时间同步问题还未见文献报道，因此，本文就这一问题展开研究，主要利用Gronwall不等式、不等式放缩技巧等导出带混合时滞的分数阶神经网络有限时间同步的充分条件，以降低分析和计算的复杂性，使所得结果更加准确。

1 预备知识

1.1 分数阶微积分的定义和引理

定义1[19]函数的α阶分数积分的定义为

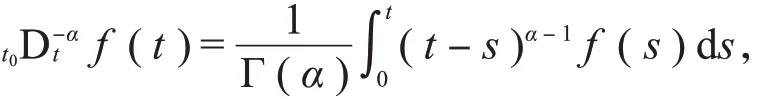
定义2[19]函数的α阶Caputo导数定义为

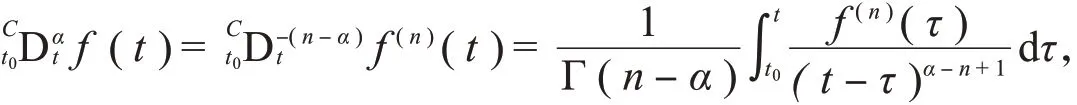
其中，t≥t0，n∈Z+，n-1＜α＜n。特别地，当0＜α＜1时

引理1[18]如果f(t)∈C n[0,+∞)且n-1＜α,β＜n∈Z+，则（1）

引理2[20]（Gronwall不等式） 假设λ＞0,0＜T＜+∞,u(t),a(t),b(t),l(t),k(t)是定义在[t0,T]上的非负连续函数，φ(t)是定义在[t0-τ,t0]上的非负连续函数，若有

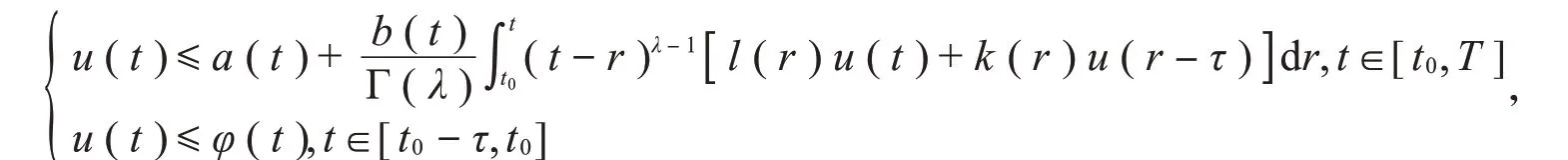
则对t∈[t0,t0+τ]，有

对t∈[t0+τ,T]，有

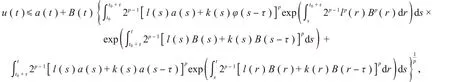
进一步讲，如果a(t),b(t),φ(t)是非递减函数，φ(t0)=a(t0)，则

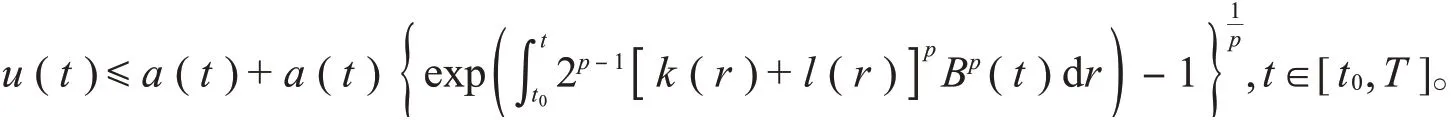
1.2 模型描述

本文所考虑的一类具有混合时滞的分数阶神经网络模型可描述为

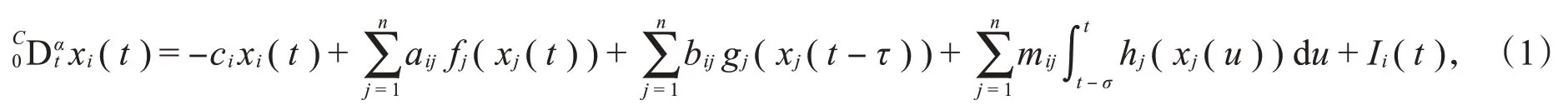
其中，0＜α＜1，x i(t)是驱动系统（1）的状态变量；f(x)表示不带时滞的激活函数，h(x)，g(x)均表示具有时滞的激活函数；c i＞0为反馈连接权重，a ij,b ij,mij是常数，分别表示第j神经元在时间t,t-τ,t-σ时与第i神经元的连接，τ,σ表示非负常数的传输延迟；I i表示外部输入偏差。

系统（1）作为驱动系统，初始条件为x i(s)=φi(s),t∈[-γ,0),γ∈max{ }τ,σ,i=1,2,3,…,n，其中，系统（1）的响应系统可表示为

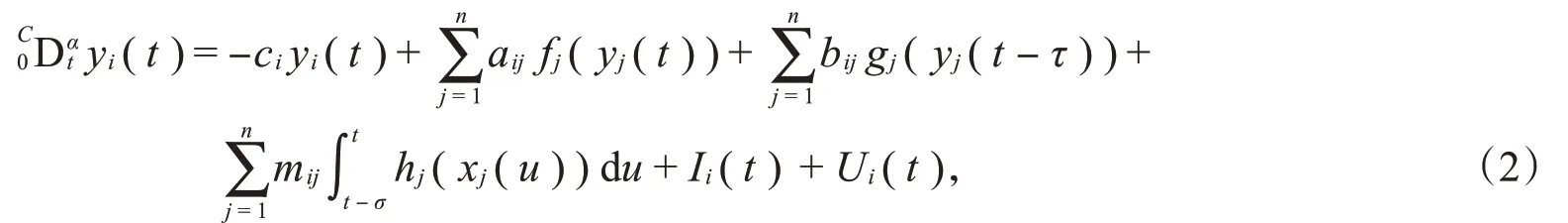
其中，y i(t)表示响应系统（2）的状态变量，U i(t)是外部控制器，其他符号与驱动系统（1）相同。系统（2）的初始值为

为了得到驱动-响应系统的同步，选取如下控制器

其中，μi＞0为控制增益。驱动系统（1）和响应系统（2）的同步误差e i(t)=y i(t)-x i(t)，则误差系统为

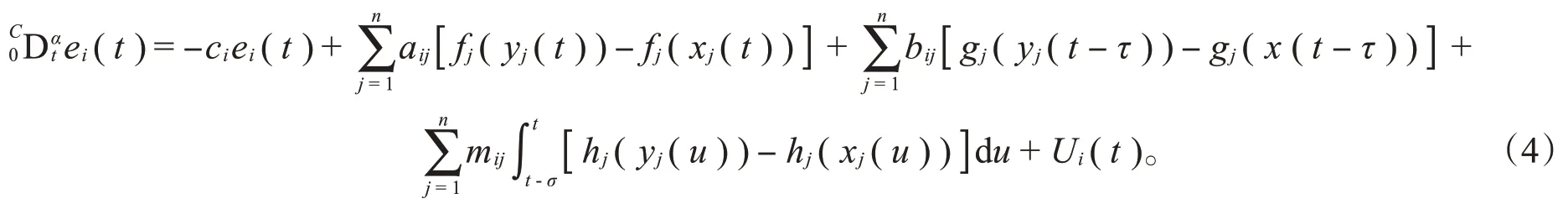
为了方便，将驱动系统、响应系统和误差系统改写为向量形式：

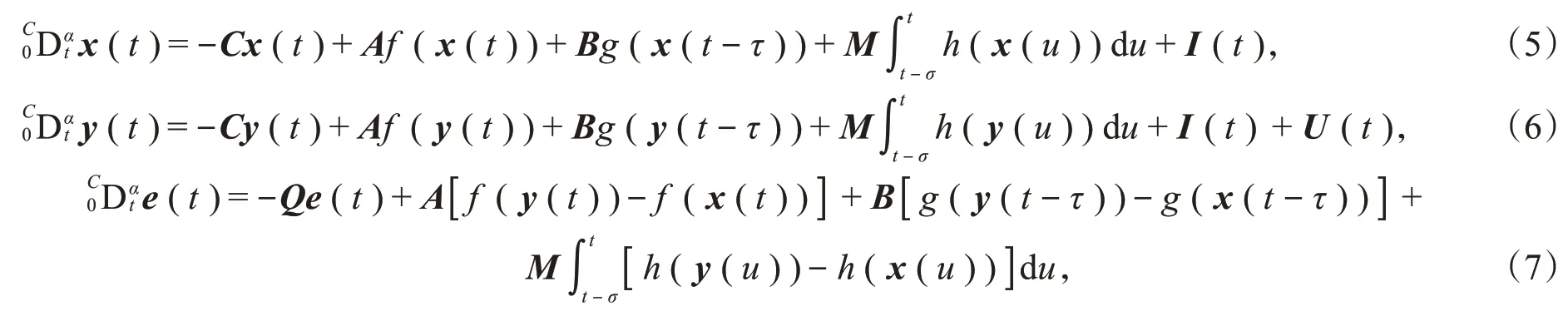
其中，Q=C+μ。

假设1神经激活函数f(x),g(x),h(x)满足：

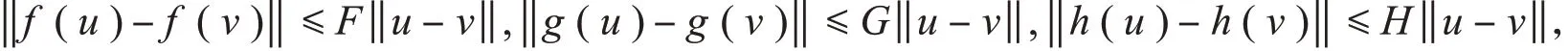
其中，F,G,H＞0，且均是Lipschitz常数，u、v∈R。

定义3[20]在控制器（3）下，驱动系统（1）和响应系统（2）在有限时间实现同步，即误差系统的状态是有限时间稳定的，若存在正数δ,ε,T，ε＞δ，当且仅当‖ψi‖＜δ，有‖e(t) ‖＜ε，对均成立。

2 主要结果

下面，利用Gronwall不等式推导一类分数阶混合时滞神经网络系统的有限时间同步的充分条件。

定理在假设1的条件下，如果满足下列条件：

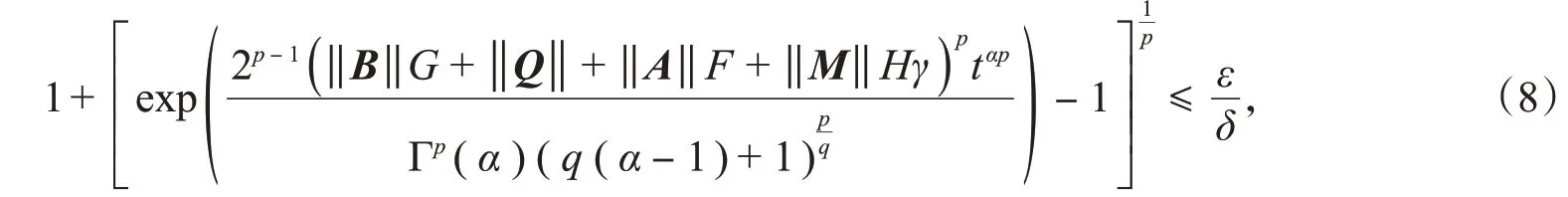
则驱动系统（1）与响应系统（2）在控制器（3）下实现有限时间同步，其中，t∈[0,T],p,q＞0使得

证明由引理1可知，对误差系统（7）进行α阶积分有

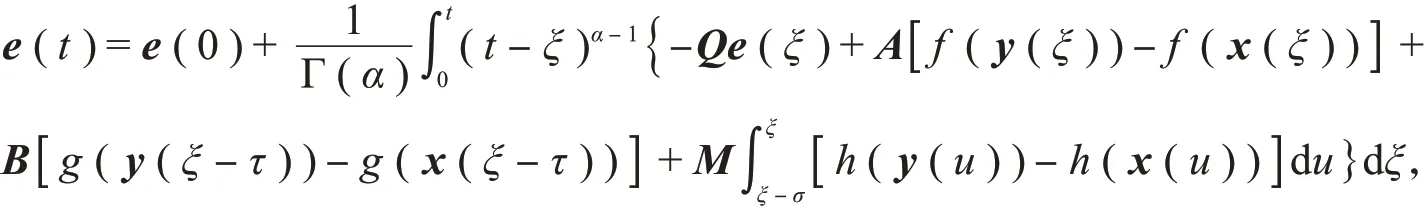
对两边取适当的范数，在假设1下有

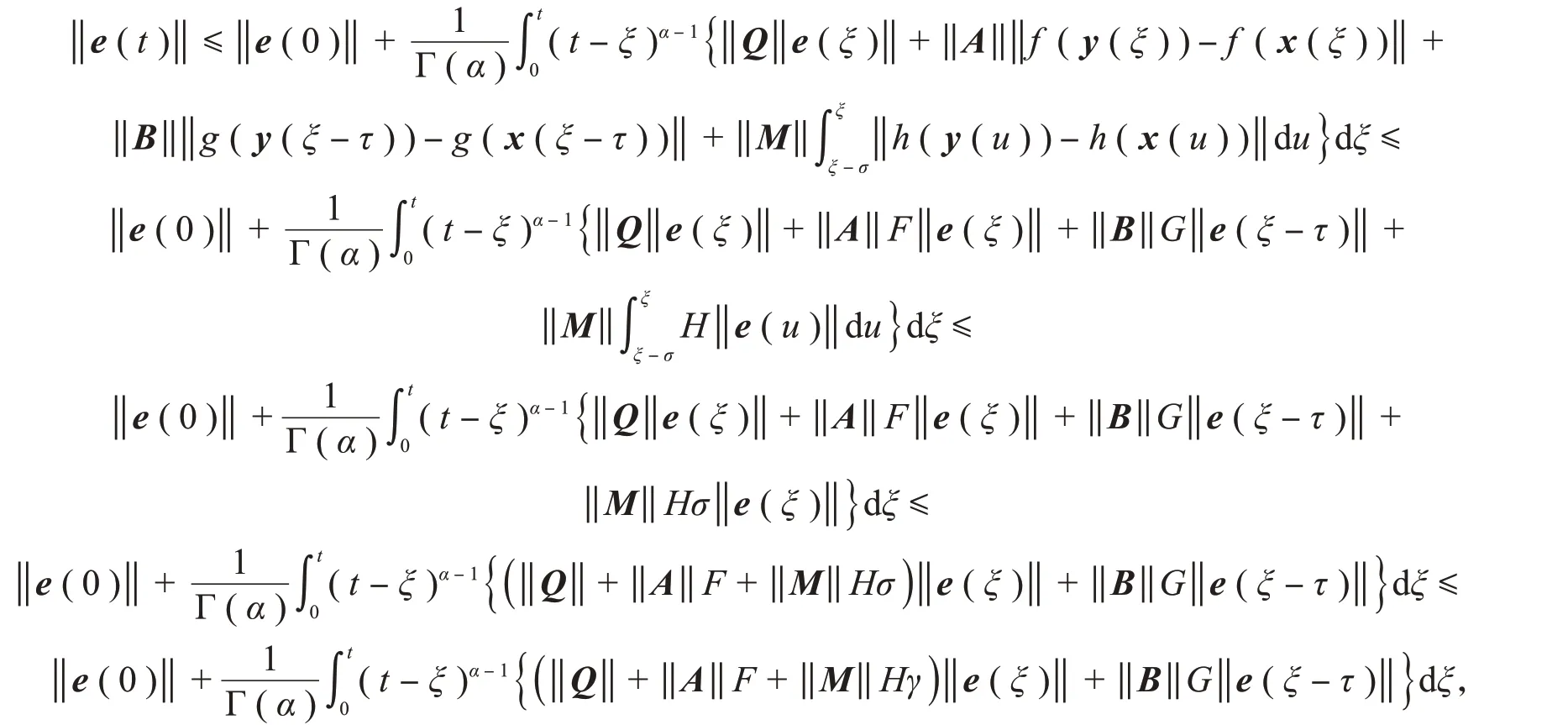
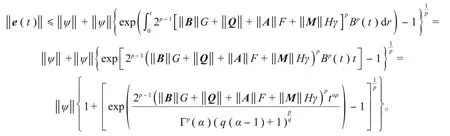
在条件（8）下，可以得到‖e(t)‖＜ε。由定义3可知：误差系统（4）是有限时间稳定的，即驱动系统（1）与响应系统（2）在控制器（3）下实现有限时间同步。

3 数值模拟

考虑一类具有混合时滞的分数阶神经网络作为驱动系统：

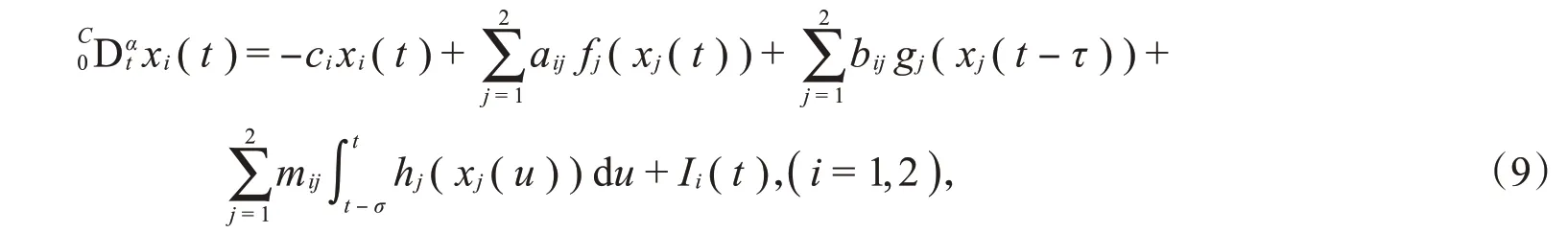
其对应的响应系统为

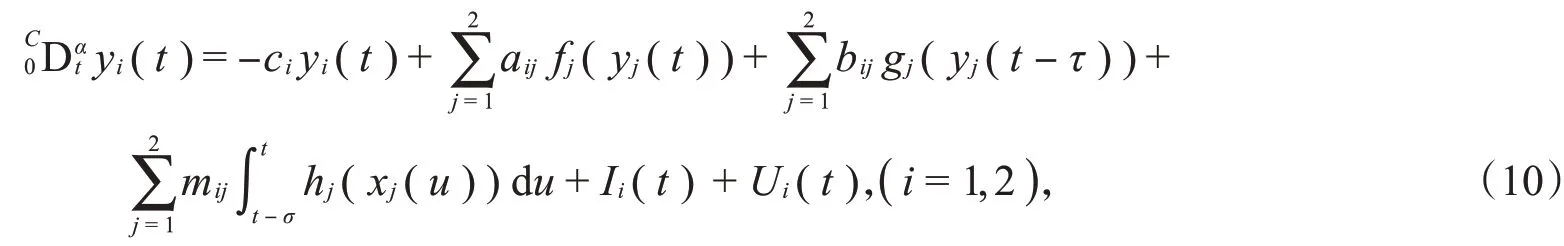
其中，激活函数取f i(x i(t))=g i(x i(t))=h i(x i(t))=tanhx。由假设1可知，F=G=H=1，参数分别为

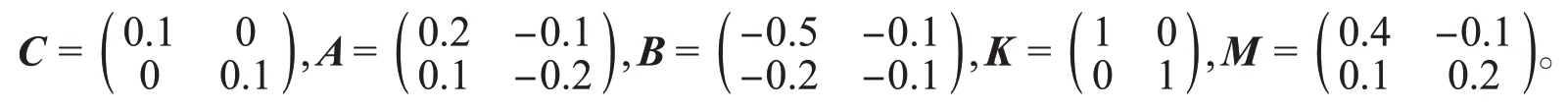
令p=2,ε=1,δ=0.01,σ=1,τ=0.4，控制器中取‖μ=1‖，由定理可得：

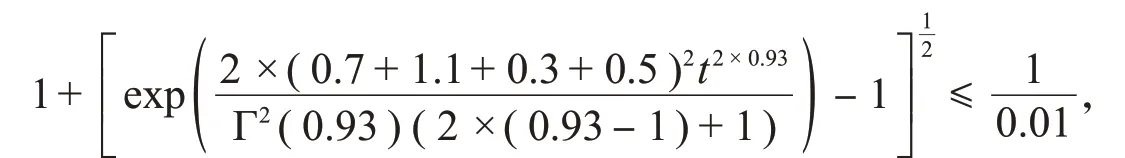
通过计算可知，同步时间T约为0.786 06。

当α1=0.93,α2=0.75,α3=0.25时，初始条件取x(t0)=0.2,y(t0)=0.1，在控制器（3）下的驱动系统（9）和响应系统（10）的误差变量e(t)的运动轨迹如图1所示，其范数‖e(t)‖的运动轨迹如图2所示。

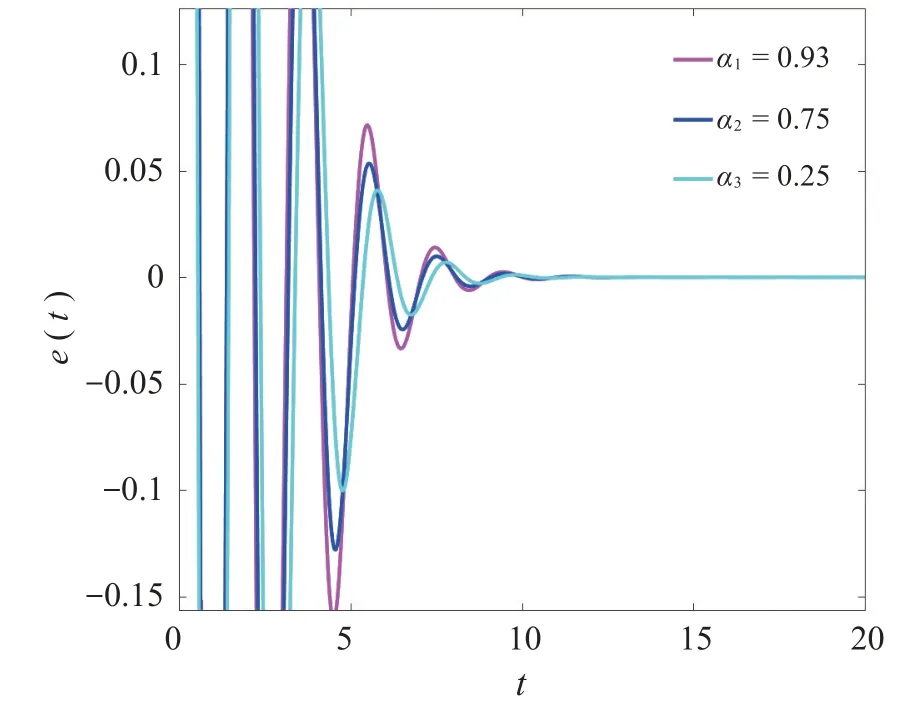
图1 e(t)的运动轨迹

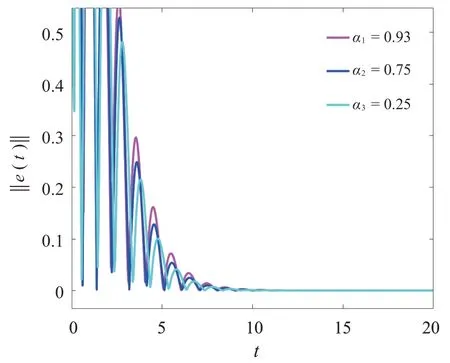
图2 ‖e(t)‖的运动轨迹

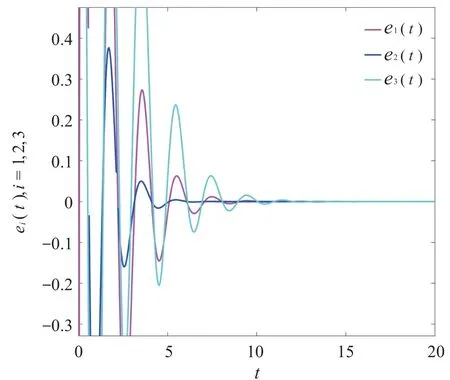
图3 e i(t)的运动轨迹

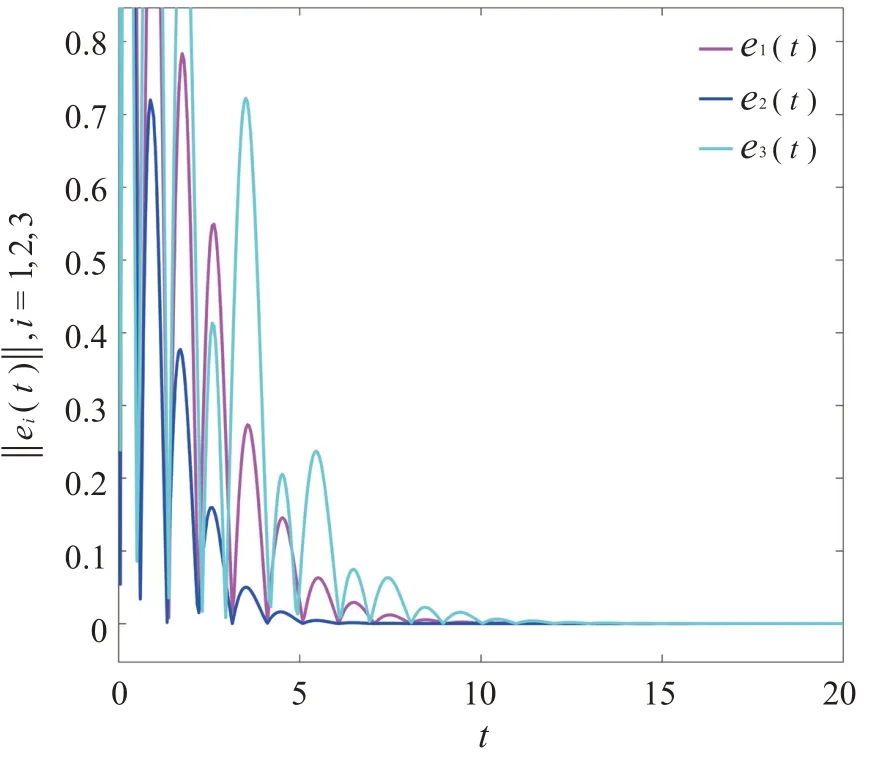
图4 ‖e i(t)‖的运动轨迹

4 结论

综上所述，本文借助具有时滞的Gronwall不等式以及一些分析技巧推导了具有混合时滞的分数阶神经网络的有限时间同步的充分判据。通过具体的数值实例证实了所得结果的正确性和可行性。值得指出的是，分数阶微积分模型在很多方面都有研究，在今后的研究课题中，也可以继续利用本文的一些分析技巧来处理其他更为复杂的模型。