圆太偏赫振兹激场光时脉H冲2+高附次加谐静波电产场生或

葛鑫磊

( 渤海大学 物理科学与技术学院，锦州 101213)

1 引 言

激光与物质相互作用时出现的非线性物理现象已经得到了人们的关注［1，2］，而高次谐波辐射就是其中热点课题之一.通过高次谐波辐射可以研究分子中电子的力学特征和分子轨道成像，同时它也是获得XUV 波段和X 射线的有效手段［3，4］，截止频率在2.33 ～4.37 nm 波段( “水窗”) 的相干X 射线［5］可以用来研究生物活体细胞.高次谐波发射( high - order harmonic generation，HHG) 呈现以下特征: 在低阶次区域急速下降，然后出现一个平台区域，接着在某一阶次迅速下降而截止.由于高次谐波强度几乎保持不变的平台结构和不同阶次谐波等频间距的特点成为理论和实验上获得阿秒(10-18s) 脉冲的有效途径.而通过阿秒科学可以研究电子的超快过程［6，7］、探索电子波包和核动力学等.

根据半经典三步模型［8］，可以对HHG 进行解释.首先，在激光场的作用下，基态电子离开原子核，电离后进入连续态.其次，电离后的电子可以当做在外场中运动的自由电子，而随着激光场周期性变化，一部分电子可以被拉回到原子核.最后，被拉回原子核的电子就有一定的几率与原子核复合从而放出高能光子，即HHG.HHG的研究已经逐渐从原子HHG 发展到结构更复杂的分子HHG.对于分子HHG［9-11］，也可以通过半经典三步模型进行描述，与原子不同的是分子中的电子可以与不同的核进行复合来发射高次谐波［12］，且分子高次谐波产生过程中核运动［13，14］、分子振动［15］和分子干涉效应［16，17］等对谐波发射影响的研究已经取得了许多进展，这为进一步完善相关动力学研究做出卓越的贡献.

人们经常选用线偏振激光脉冲作为驱动，线偏振激光脉冲作用下的谐波具有线偏振特性，而对于线偏振谐波的研究已经取得了许多创新性的成果［18-20］，实验上也已经通过高次谐波获得了43as［21］和53as［22］的超短线偏阿秒脉冲.而当圆偏振激光脉冲( circularly polarized laser pulse，CPLP)与原子或分子相互作用时，电子电离后将远离原子核，无法与原子核复合，所以HHG 强度非常低，因此，如何确保电子回复是至关重要的问题，人们对CPLP 下电子回复问题及HHG 已经展开了研究［23］.

在我们之前的工作中，研究了CPLP 作用下的HHG，通过在CPLP 的y 方向附加一个太赫兹场( terahertz，THz) ，可以成功的把电子拉回到母核而得到高次谐波，最后，通过附加一个强度为0.06 a.u.的THz 场，得到了带宽为225 eV 的连续谱［24］.在此基础上，我们还考虑了不同的THz场强度下的HHG，研究表明随着THz 场强度的增加，对谐波产生贡献的轨道逐渐从长轨道变为短轨道，实现了量子轨道的调控［25］.CPLP 附加THz场获得高次谐波的原理是破坏电子在外场中周期性运动，从而实现把电子拉回母核，而CPLP 附加静电场也可以对电子的周期性运动进行破坏，但是附加静电场和THz 场对HHG 的结果可能产生不同的影响，值得细致研究.

本文通过数值求解二维含时薛定谔方程理论的研究了CPLP 作用下H+2的高次谐波产生.对CPLP 附加静电场和CPLP 附加THz 场时的高次谐波发射谱进行对比.利用半经典三步模型、时频分析和电子波包随时间演化等对谐波发射物理机制进行研究，研究结果将对实验起到指导性作用.

2 计算方法

本文数值求解二维的含时薛定谔方程，研究了CPLP 附加静电场或附加THz 场与H+2相互时的HHG.初态波函数利用虚时演化法求得，再利用分裂算符法求解含时波函数［26］.二维含时薛定谔方程形式如下:

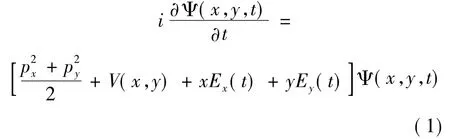
其中势能为软核库仑势:

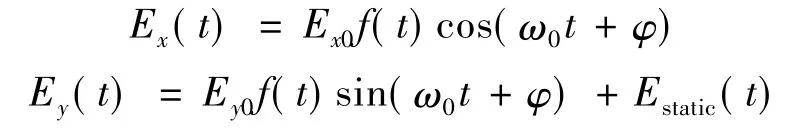
或

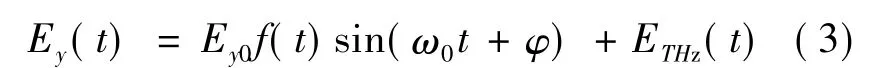
其中，静电场形式为Estatic( t)=Estatic，THz 场的形式为为入射激光脉冲包络，T 是波长为800 nm( 频率为ω0=0.057 ) 的激光的光学周期，我们选取6 个周期( n=6 ).Ex0和Ey0为CPLP 在x 和y 方向的峰值强度，光强选为Ix0=Iy0=5 ×1014W/cm2( 即Ex0=Ey0=0.1194 a.u.).附加的静电场或THz场强度选取为Estatic=ETHz=0.03 a.u..THz 场波长λ=9600 nm( 对应频率ωTHz=31.25 THz).φ=-0.1π 为相对相位.

3 结果与分析

CPLP 的x 和y 方向分量是相同的，当在CPLP 的x 或y 方向上附加静电场或THz 场相当于破坏了CPLP 的对称性.我们在y 方向附加静电场或THz 场，x 方向的激光场不会发生变化，所以在下文中着重分析y 方向谐波发射情况.图1 给出了CPLP 以及CPLP 的y 方向附加静电场或附加THz 场后的激光场形式.从图中可以看出，附加静电场或THz 场可以使激光场的强度提高，但并不会影响激光场的整体形状.在中心峰值区域( 2-4 周期) 附加静电场或THz 场时的激光场是十分相似的，区别主要体现在前后两个周期( 0 -2 和4 -6 周期).当附加静电场时，激光场的强度在6个周期内整体被提高，而附加THz 场时，只是2-4 周期的强度被加强，激光场的前后两个周期强度和只有CPLP 时相比几乎没有变化，也就是说静电场的加入将提高整个激光场的强度，而THz 场的加入只对中心区域的峰值强度进行了加强.

图1 激光场图像.黑色实线: 只有CPLP.红色点虚线: CPLP 附加静电场.蓝色杠虚线: CPLP附加THz 场.Fig.1 Laser field.solid black line: a circularly polarized laser pulse( CPLP) ; dotted red line: a CPLP combined with a static electric field;dashed blue line: a CPLP combined with a terahertz ( THz) field.

图2 给出了CPLP、CPLP 附加静电场和CPLP附加THz 场时的HHG 图像.从图中可以看出，在只有CPLP 时，谐波强度非常低，说明电子电离后无法回到母核与母核复合.当在CPLP 的y 方向附加静电场或THz 场时，谐波效率提高5 个量级左右，确保了CPLP 下电子与母核的复合.当CPLP 附加静电场时，谐波的截止位置为208 eV，呈现出双平台，且谐波谱布满调制结构，也就是说在谐波发射过程中产生贡献的量子轨道之间干涉较严重.而当CPLP 附加THz 场时，我们得到了一个，带宽大约为122 eV 的连续谱，谐波谱比较平滑，说明量子轨道之间干涉较小.

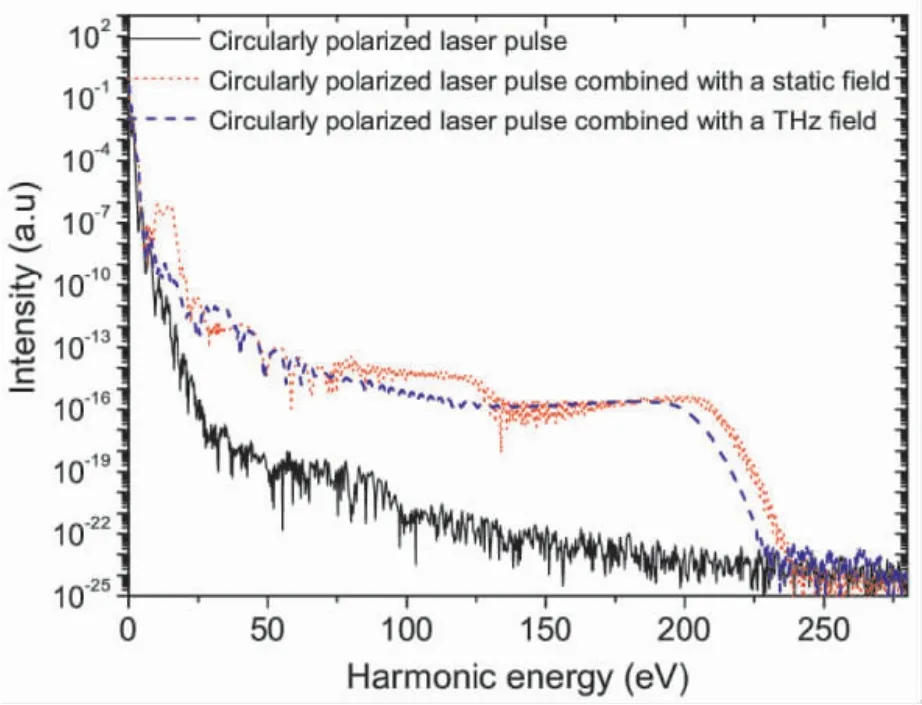
图2 高次谐波谱.黑色实线: 只有CPLP; 红色点虚线: CPLP 附加静电场; 蓝色杠虚线: CPLP 附加THz 场.Fig.2 High - order harmonic spectra.Solid black line:only CPLP; dotted red line: a CPLP combined with a static electric field; dashed blue line: a CPLP combined with a THz field.

我们应用小波变换方法计算了谐波的时频分析图像，图3( a) 和( b) 分别代表CPLP 附加静电场时和CPLP 附加THz 场时HHG 的时频分析图像.CPLP 附加静电场后( 图3( a) ) ，主要有三个峰对谐波发射产生贡献，分别标为P1，P2和P3.在135 eV 以下，P1，P2和P3都对谐波发射产生贡献，且三个峰强度相当.而在135 eV 以上，对谐波产生贡献的是P2峰的长轨道和P3峰的短轨道( 正的上升沿对应的是短轨道，负的下降沿对应的是长轨道) ，所以在135 eV 左右谐波出现双平台结构，对应图2 中红色点虚线所示.从图3( b)中可以看出，当附加THz 场后，对谐波发射产生贡献的峰标为P1，P2和P3.P3峰的强度相对于P1和P2来说非常的弱，可以忽略不计，而P1的强度要弱于P2峰，所以P2峰对谐波发射产生主要贡献.且在90 eV 以上，对谐波产生贡献的就只剩下P2峰的长轨道，所以得到了谱宽大约为122 eV的连续谱，对应图1 中蓝色杠虚线所示.

图3 时频分析.( a) 、( b) 分别对应CPLP 附加静电场和CPLP 附加THz 场.Fig.3 The time-frequency distributions of the highorder harmonic spectra corresponding to ( a) the dotted red curve，and ( b) the dashed blue curve in figure 2.

接着我们通过随时间演化的电子波包概率分布图像来研究CPLP 附加静电场和THz 场后对电子运动的影响，如图4 和5 所示.从4( a1) -( a20) 中( CPLP 附加静电场) 可以看出，随着时间演化，电子密度流沿逆时针转动.在1.4 o.c.左右电子开始电离，随着时间演化，电子以一定的半径向外运动，而静电场的加入，破坏了CPLP的x 和y 方向对称性，相当于在y 方向对电子产生了一个外力作用，可以将电子拉回到原子核附近.所以，在6 个周期内电子一共三次与母核复合，分别发生在t=2.4 o.c.、t=3.5 o.c.和t=4.5 o.c.( 如图4( a9) 、( a15) 和( a19) 中白色箭头所示) ，这三个复合时间和时频分析3( a) 中三个量子峰产生的时间完全一致.当加入THz 场时，出现的现象有所不同，如图5( b1) - ( b10) 所示( CPLP 附加THz 场) ，电子在2.3 o.c.才开始电离，这个时间比加入静电场时晚了一个周期，而且电子仅有两次与母核复合，第一次复合发生在t=3.5 o.c.( 如图5( b5) 中白色箭头所示) ，第二次复合发生在t=4.5 o.c.时( 如图5( b10) 中白色箭头所示).通过电子波包概率分布，可以清楚的看到电子在t=3.2 o.c.和t=4.7 o.c.时刻两次与母核复合发射高次谐波，而刚好与时频分析中的量子峰P2和P1的产生时间对应.

图4 CPLP 附加静电场时电子波包概率分布随时间演化图像.Fig.4 The temporal evolution of the probability density of the electron wave packet for the CPLP combined with the static electric field.

图5 CPLP 附加THz 场时电子波包概率分布随时间演化图像.Fig.5 The temporal evolution of the probability density of the electron wave packet for the CPLP combined with the THz field.

为了更直观的看到电子运动情况，我们给出了1.5 o.c.-4.5 o.c.过程中，电子波包概率分布随时间的演化图像.从图6 中可以看出，在2.5 o.c.之后的电子波包图像是几乎相同的，所以我们着重研究1.5 o.c.到2.5 o.c..在图6( a)中( CPLP 附加静电场) ，在1.5 o.c.有大量的电子电离，接着，激光场反向，在t=2.4 o.c.左右，部分电子被拉回到母核附近与母核复合( 如图6( a) 中白色虚线框所示) ，从而发射高次谐波，这就是时频分析图3( a) 中的P3峰的产生.而在图6( b) 中( CPLP 附加THz 场) ，在2.0 o.c.之前，几乎没有电子电离，所以在2 o.c.到2.5 o.c.周期内谐波效率非常的低，这与图3( b) 中时频分析图像是吻合的.

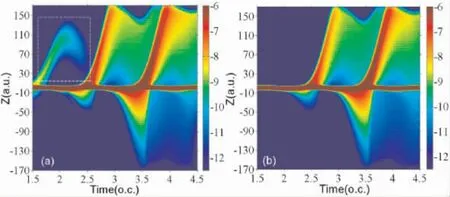
图6 电子波包的概率分布随时间的变化( 1.5o.c.-4.5o.c.).( a) 、( b) 分别对应CPLP 附加静电场和CPLP 附加THz 场.Fig.6 The electronic probability densities.( a) The CPLP combined with the static electric field，and ( b) the CPLP combined with the THz field.

为了深入了解HHG 的物理机制，我们给出电离几率和三步模型图像，如图7 和8 所示.图8( a) 为CPLP 附加静电场时的三步模型图像，图中出现三个量子峰对HHG 产生贡献，分别标记为A1、A2和A3，回复时间为2.5 o.c.、3.5 o.c.和4.5 o.c.，对应的电离时间分别为1.4 o.c.、2.4 o.c.和3.4 o.c..配合电离几率图像分析发现，1.4 o.c.、2.4 o.c.和3.4 o.c.三个时间都有电子发生电离，所以对应的A1、A2和A3三个峰对谐波发射都产生贡献，这与时频分析和电子波包的概率分布图中所得到的结果一致.图8( b)是CPLP 附加THz 场时的三步模型图像，HHG 同样自于三个量子峰，标记为B1、B2和B3.B1、B2和B3的发射时间为2.5 o.c.、3.5 o.c.和4.5 o.c.，对应的电离时间是1.4 o.c.、2.4 o.c.和3.4 o.c..但是配合电离曲线发现，电子在2.0 o.c.之前是几乎没有电离，所以在2.5 o.c.左右发射的谐波( 对应电离时间1.4 o.c.) 忽略不计，这与时频分析中的结果吻合，即图3( b) 中P3的相比于P1和P2来说很弱，对HHG 不产生贡献.从图8( b) 我们还可以观察到，电子在3.5 o.c.左右和4.5 o.c.左右与母核复合，对应的能量分别为208 eV 和86 eV.能量高于86 eV 时，B3峰对HHG 是没有贡献的，因此86 eV 以上的HHG 均来自于B2峰.故得到了一个带宽为122 eV 的连续谐波谱，这与图2 中谐波谱图像完全吻合.

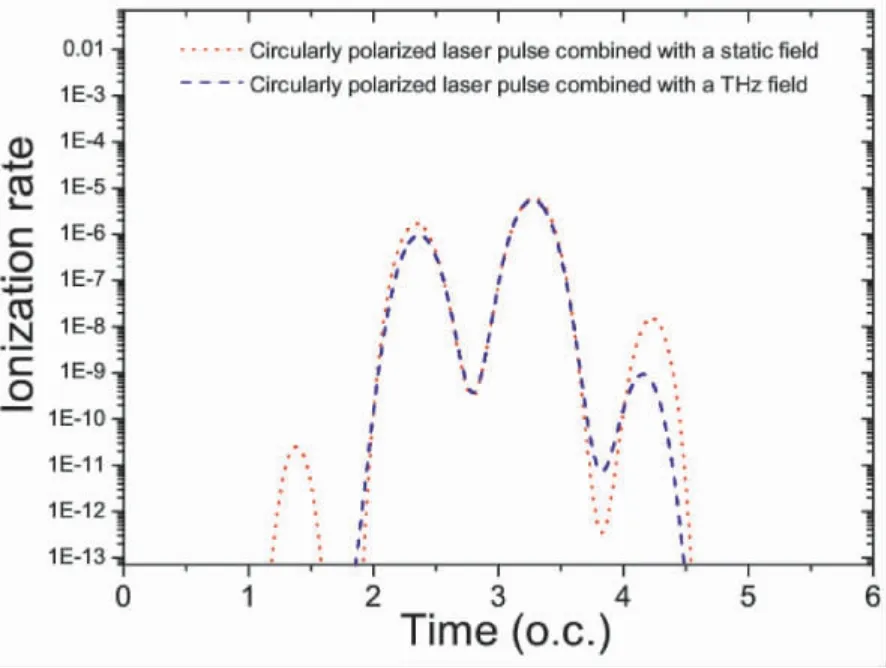
图7 电离几率.红色点虚线代表CPLP 附加静电场，蓝色的杠虚线代表CPLP 附加THz 场.Fig.7 The time dependences of the ionization rate calculated by the ADK theory.Dotted red line: a CPLP combined with a static electric field;dashed blue line: a CPLP combined with a THz field.

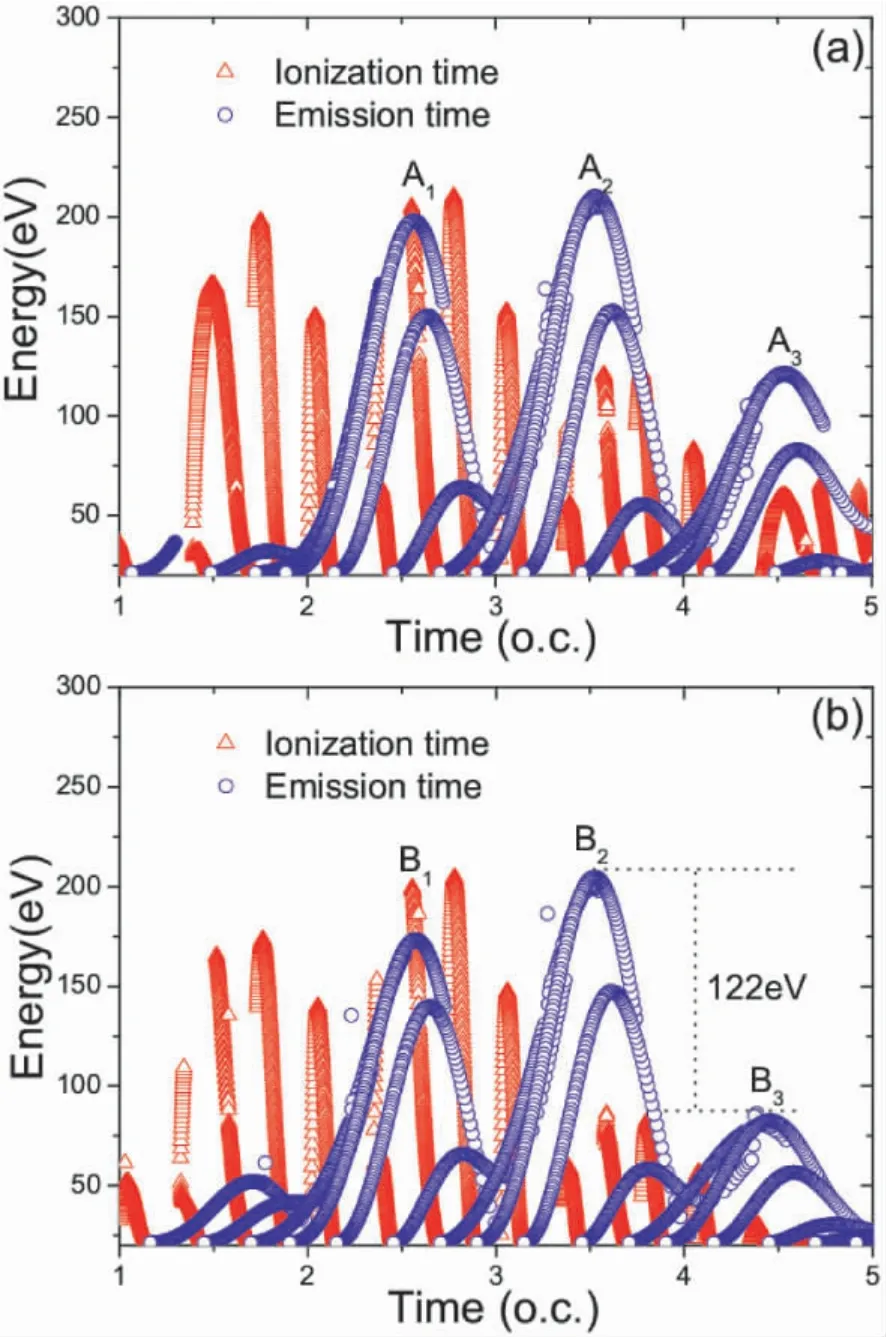
图8 半经典三步模型.( a) 、( b) 分别对应CPLP附加静电场和CPLP 附加THz 场.红色的三角表示电离，蓝色的圆圈表示复合.Fig.8 The dependences of the energy on the ionization( red triangles) and emission times ( blue circles) for ( a) the CPLP combined with a static electric field，and ( b) the CPLP combined with a THz field.

4 结 论

本文通过数值求解二维含时薛定谔方程，理论的研究了CPLP 附加静电场或附加THz 场对HHG 的影响及区别.研究表明，CPLP 的x 和y 方向是相同的，在某一个方向附加静电场或THz 场可以使这个方向上激光场强度提高，但并不会影响激光场的整体形状，而某一个方向上激光场峰值强度变大，就破坏了CPLP 的x 和y 方向的对称性，相当于这个方向的电子受到一个外力作用，可以将其拉回到原子核附近.而附加静电场或THz 场区别体现在，附加静电场时，激光场的强度整体被提高，而附加THz 场时只对中心区域的峰值强度进行了加强.从谐波谱图像上我们发现，附加静电场时，谐波呈双平台结构，且谐波谱布满调制，结合时频分析，电子三次与母核复合发射高次谐波，量子轨道之间干涉较严重.当对CPLP 附加THz 场时，电子只有两次与母核复合，轨道之间的干涉减少，故得到了一个带宽为122 eV 的连续谱.这说明，静电场的加入对激光场强度整体提高并非全部有效，反而会让量子轨道之间产生严重的干涉，从而影响高次谐波发射谱，相比于附加静电场，THz 场仅对中心区域激光场峰值进行加强，起到更好地作用.我们还研究了初速度不为零的半经典三步模型和电子波包随时间演化的概率分布等，结果都与时频分析吻合.