井下磁耦合无线电能传输系统的全谐振特性分析
张莲, 杨洪杰, 经廷伟, 李涛, 张路
(重庆理工大学 电气与电子工程学院, 重庆 400054)
0 引言
煤矿井下大功率电力设备在采用煤油燃气作为燃料时产生的粉尘、尾气在井下不通风的环境下不易排放,采用电能传输时会减少污染,但裸露的插口在开关过程中易产生火花,电线易老化;狭窄的巷道和工作面无法为井下监控系统及照明系统提供有线供电线路,只能采用容量电池供电,然而电池的容量有限,无法保证工作时长,无线电能传输(Wireless Power Transfer,WPT)技术的出现与发展为井下复杂环境的供电提供了可能。
在井下巷道有限空间内,主要应用的WPT技术有微波式、电磁感应式和磁耦合谐振式。微波式和电磁感应式WPT通过放射电磁波进行能量传输,对人体有辐射影响且存在安全隐患。磁耦合WPT(Magnetic Coupling,MC-WPT)利用高频逆变、磁场耦合等技术实现能量传输,具有传输效率高、传输有效距离范围广、安全性高等优点[1-4]。煤矿井下含有易燃易爆气体,发射功率不能超过6 W,目的是为了避免电磁场在远场区产生的电磁波辐射到金属刀片上产生热效应引起爆炸,但在一定范围内,MC-WPT技术在近场区(米级范围)可实现发射源产生不向外辐射的交变磁场,从而实现发射级宽范围搭载功率(在理论意义上发射功率可以较宽调节,但该技术目前仍在理论研究阶段)[5-8]。
MC-WPT技术现主要应用在安装有防爆装置的井下配电房或变电所,对矿井大功率运输设备如采掘车、猴车等电力设备的蓄电池充电。对矿井安全监控系统的传感器进行无线输电,由于磁能发射与拾取机构的完全电气隔离,电气设备安装、检修、移动都较灵活,可以有效保障井下电气设备的安全与灵活供电[7-8]。
在井下应用MC-WPT系统供电时,由于系统的强耦合性,如果系统参数配置不当将会引起系统输入阻抗呈现非纯阻性,从而造成系统失谐。失谐状态下的MC-WPT系统无功功率增大,谐波增加,功率因数、输出功率和输出效率降低,影响井下电力设备的供电效率,所以对MC-WPT系统进行全谐振优化配置尤为重要。在MC-WPT系统中,低阶补偿及高阶补偿存在不同的谐振特性[9-14],在保证全谐振的情况下,需根据拓扑特性选择适合煤矿井下应用的MC-WPT系统。
文献[15]为解决煤矿井下大量无线传感器节点电池更换问题,建立了井下移动式充电模型,利用MC-WPT系统对煤矿井下无线传感器进行充电。文献[16]针对传统串联-串联(Series-Series,SS) 、串联-并联(Series-Parallel,SP)、并联-串联(Parallel-Series,PS)、并联-并联(Parallel-Parallel,PP)4种补偿基本拓扑的缺点,在综合考虑煤矿井下瓦斯、粉尘对用电安全影响的基础上,提出了一种煤矿井下电气设备无线供电系统,通过与纯互感耦合模型阻抗模频率特性进行对比分析,保证系统全谐振工作的同时,得出了系统最优化谐振频率计算方法。文献[17]通过分析SS型MC-WPT系统模型,推导了使系统保持全谐振频率的负载电阻和传输距离范围。文献[18]为解决矿灯因锂电池容量有限而无法长时间工作及在井下充电存在安全隐患等问题,利用二次侧并联型MC-WPT系统,设计了一种可在井下无线充电的矿灯。文献[19]在煤矿井下运输装备特定的传输距离约20 cm的情况下,搭建了改进三线圈结构的MC-WPT系统,采用传统串联电容方式来抵消线圈互感对系统的影响,在实现系统全谐振的同时提高了系统传输效率和传输功率。文献[20]针对煤矿井下复杂的应用场景,以SS型拓扑为基础,提出了一种改进四线圈的MC-WPT系统,提高了电能传输功率。文献[21]建立了井下谐振耦合WPT系统的等效模型,分析了负载电流和谐振线圈电感变化量的特性,提出了一种基于负载电流和谐振线圈电感变化量的鲁棒性衡量系数。
MC-WPT系统二次侧采用串联补偿时易实现谐振,但在二次侧采用并联补偿时,现有研究都是在系统仅一次侧谐振、二次侧未谐振,造成系统阻抗呈感性,从而导致系统未全谐振的基础上进行的。针对该问题,提出一种全谐振补偿方式,在系统体积、成本不增大的基础上,通过系统阻抗分析得到补偿电容的计算方式,使系统一次侧及二次侧电路完全谐振,并通过互感跃变实验分析对比了SP型、PP型、LCC-P型和LCL-P型4种二次侧并联拓扑的全谐振特性,得出SP型MC-WPT系统更适合应用于煤矿井下。针对井下传输设备在线路老化、运作时长及环境因素等影响下负载容易产生变化的问题,对SP型补偿方式进行优化,通过仿真和实验对理论分析进行了验证。
1 二次侧并联MC-WPT系统传统补偿方式
以SP型、PP型、LCC-P型和LCL-P型补偿拓扑作为二次侧并联MC-WPT系统研究对象。二次侧并联MC-WPT系统模型如图1所示。其中,VDC为直流电压源(注:PP型补偿拓扑需提供稳定电流源);Q1—Q4为全控型开关管,组成全桥逆变电路;Vi为一次侧补偿结构输入电压;Ii为一次侧补偿结构输入电流;IP为一次侧补偿结构输出电流;LP为一次侧补偿电感;M为互感;LS为二次侧补偿电感;CS为二次侧补偿电容;RL为电阻负载;IS为流经LS的电流;RP,RS分别为LP,LS的内阻。
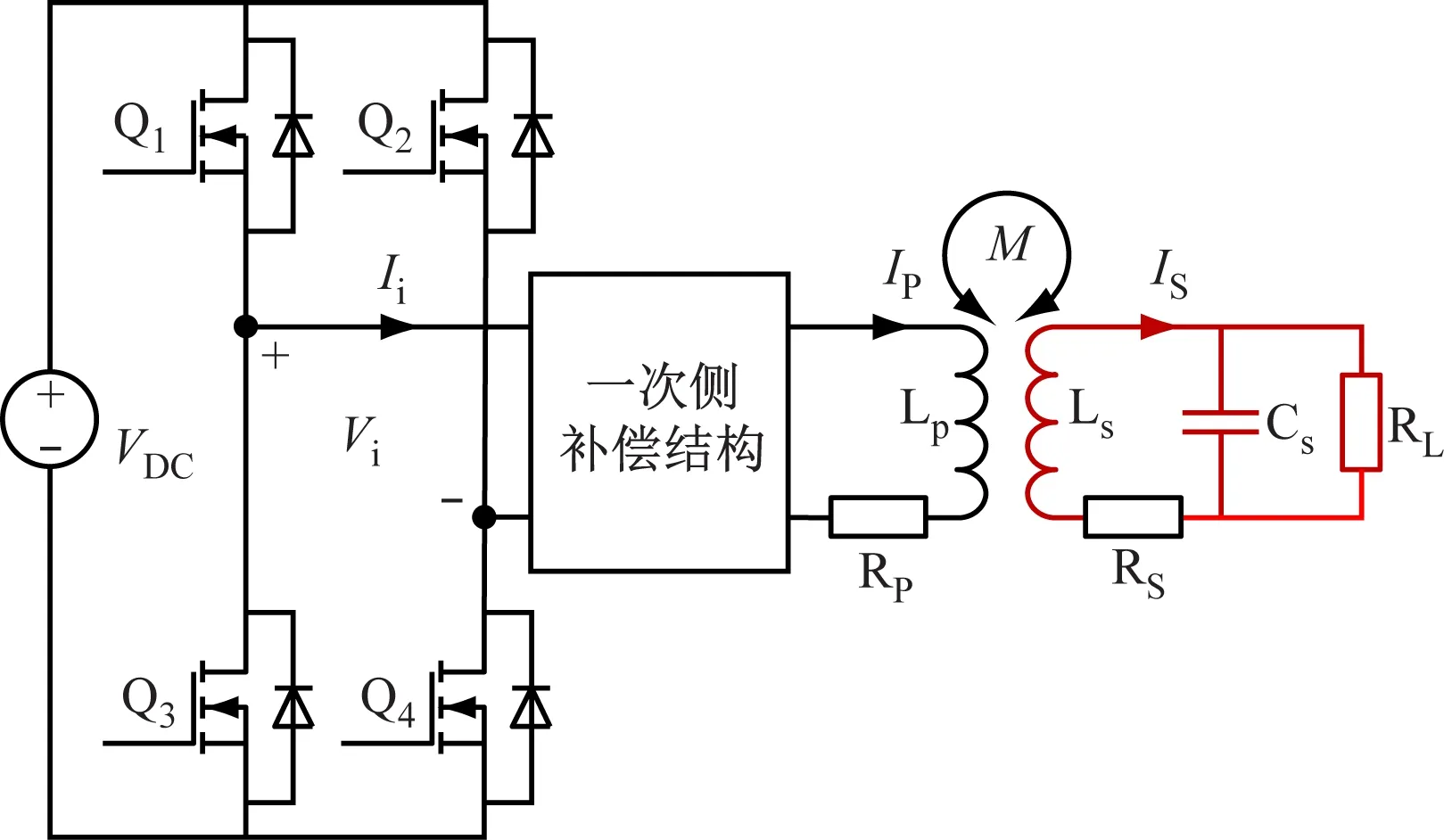
图1 二次侧并联MC-WPT系统模型Fig.1 MC-WPT system model of secondary side parallel
SP型、PP型、LCC-P型和LCL-P型补偿拓扑的一次侧补偿结构由补偿电感LT和补偿电容CP,CT的不同组合构成,如图2所示,其中RT为LT的内阻。利用交流阻抗分析法从频域角度对系统进行分析。由于4种补偿拓扑二次侧补偿结构相同,可得二次侧并联MC-WPT系统的二次侧阻抗ZS及二次侧反射至一次侧的等效阻抗ZR:
(1)
式中ω为系统工作角频率。


图2 一次侧补偿结构Fig.2 Primary side compensation structure
SP型、PP型、LCC-P型和LCL-P型补偿拓扑的一次侧阻抗为
(2)
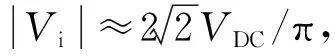
(3)
式中:Pi为一次侧电源提供的有功功率,即系统输入功率;P0为二次侧电阻负载消耗的有功功率,即系统输出功率。
为提高系统功率传输能力,利用谐振原理对系统进行无功补偿,使系统工作在谐振状态,即ω=ω0,ω0为系统谐振角频率。针对系统二次侧并联补偿结构,采用传统补偿方式时,ω0计算公式为
(4)
系统处于谐振状态时,系统二次侧阻抗为
(5)
由于内阻对补偿电容的影响较小,为便于分析计算,在计算补偿电容时不考虑内阻影响。利用式(2)和式(5)可得传统补偿方式下,SP型、PP型及LCL-P型补偿拓扑一次侧补偿电容表达式:
(6)
(7)
(8)
传统补偿方式下LCC-P型补偿拓扑的一次侧补偿电容表达式为[14]
(9)
传统补偿方式仅保证了SP型、PP型及LCL-P型补偿拓扑一次侧电路处于谐振状态,二次侧并未谐振;而LCC-P型补偿拓扑由于其一次侧具有3个谐振回路,其一次侧补偿电容的特殊性造成一、二次侧均未谐振。MC-WPT系统未谐振会造成补偿电容的电能与电感的磁能无法完全相互转换,电源需提供一定的无功功率,对系统传输功率、效率及功率密度均有一定影响。
2 全谐振补偿方式
在式(1)的基础上,令二次侧阻抗虚部为零,得到谐振时二次侧补偿电容表达式,从而得到一次侧补偿电容的表达式,保证系统两侧电路均处于谐振状态,呈纯阻性。系统二次侧阻抗虚部为
(10)
令式(10)为零,得到全谐振补偿方式下二次侧并联MC-WPT系统的二次侧补偿电容表达式:
(11)
为保证二次侧补偿电容存在有效值,需满足RL≥2ω0LS。当系统处于谐振状态时,全谐振补偿方式二次侧阻抗为
(12)
根据式(2),可得全谐振补偿方式下一次侧补偿电容在忽略内阻影响时的表达式。
(13)
(14)
(15)
LCC-P型补偿拓扑在全谐振补偿方式下的一次侧补偿电容表达式仍为式(9)。全谐振补偿方式下,系统一次侧、二次侧均处于完全谐振状态。对于SP型补偿拓扑,全谐振补偿方式下系统的谐振频率仅受电阻负载的影响,且一次侧补偿电容计算方式仅与一次侧补偿电感有关。
3 仿真分析
为使二次侧并联MC-WPT系统传统补偿方式和全谐振补偿方式的对比分析更准确,在相同参数(补偿电容取值不同)下,利用Matlab/Simulink对2种补偿方式进行仿真对比。仿真参数:VDC=24 V,LP=100 μH,RP=0.2 Ω,LCC-P型拓扑LT=20 μH, LCL-P型拓扑LT=50 μH,LCC-P型拓扑RT=0.04 Ω,LCL-P型拓扑RT=0.1 Ω,LS=100 μH,RS=0.2 Ω,M=30 μH,谐振频率f0=22 kHz,补偿电容可由式(6)、式(9)、式(11)及式(13)求得。
随着电阻负载变化,传统补偿方式与全谐振补偿方式的输出功率比值变化如图3所示。可看出SP型、PP型和LCL-P型补偿拓扑在全谐振补偿方式下的输出功率大于传统补偿方式下的输出功率,随着电阻负载增大,输出功率差值逐渐减小;LCC-P型补偿拓扑在全谐振补偿方式下的输出功率小于传统补偿方式下的输出功率。
传统补偿方式与全谐振补偿方式下的系统效率随电阻负载变化如图4所示。可看出SP型与PP型补偿拓扑的效率有着相似的变化趋势,且在全谐振补偿方式与传统补偿方式下相差不大;LCC-P型补偿拓扑在全谐振补偿方式下的效率远高于在传统补偿方式下的效率;LCL-P型补偿拓扑在传统补偿方式下的效率略高于在全谐振补偿方式下的效率。
在相同输出功率(100,200,300 W)下,二次侧并联MC-WPT系统在全谐振补偿方式与传统补偿方式下的视在功率(系统输出有功功率与无功功率总和)对比如图5所示。
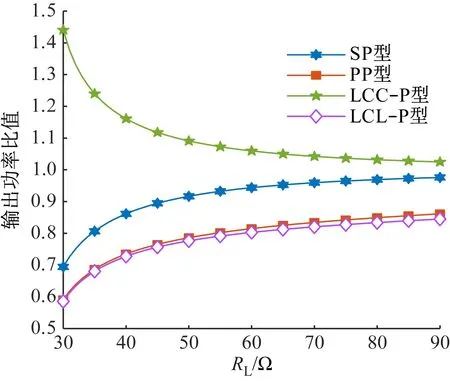
图3 输出功率对比Fig.3 Output power comparison
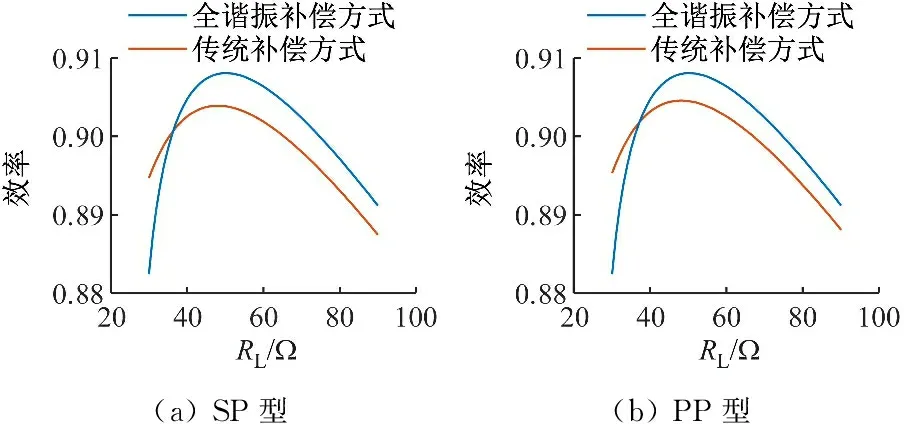

图4 系统效率对比Fig.4 System efficiency comparison
从图5可看出,在全谐振补偿方式下一次侧与二次侧电路均处于谐振状态,系统呈纯阻性,所以4种补偿拓扑的视在功率等于给定的输出功率,系统无需提供无功功率;而在传统补偿方式下二次侧电路未谐振,系统不仅需提供有功功率,还需提供无功功率,因此在输出功率相等的前提下,传统补偿方式下系统的视在功率和功率密度较大。
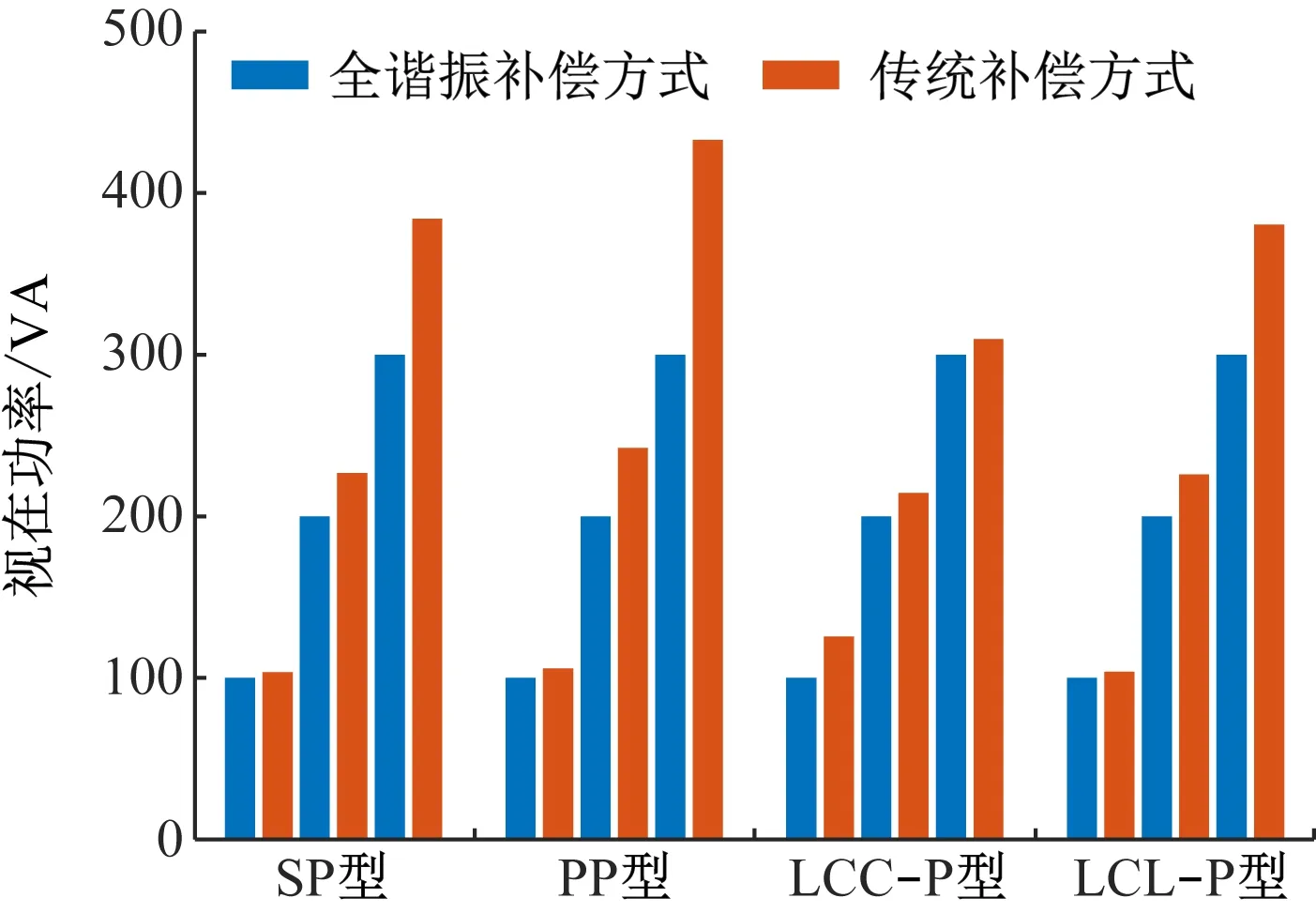
图5 视在功率对比Fig.5 Apparent power comparison
从式(6)、式(9)、式(11)及式(13)可发现,PP型及LCL-P型补偿拓扑的一次侧补偿电容表达式较复杂,系统谐振频率均受到互感及电阻负载的影响。4种补偿拓扑在全谐振补偿方式下,系统谐振频率均受到电阻负载的影响,且电阻负载需满足RL≥2ω0LS。SP型补偿拓扑在全谐振补偿方式下,系统谐振频率仅受电阻负载的影响,摆脱了互感的束缚。在Simulink中搭建仿真电路,测得互感及电阻负载跃变时,SP型补偿拓扑一次侧功率因素的变化(图6),分析参数变化对系统谐振状态的影响。
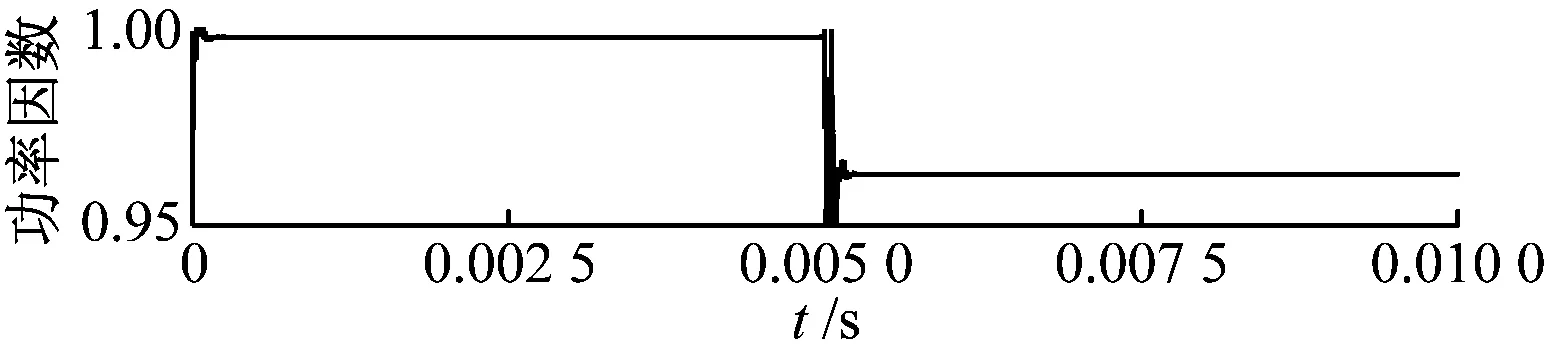
(a) 传统补偿方式下互感跃变
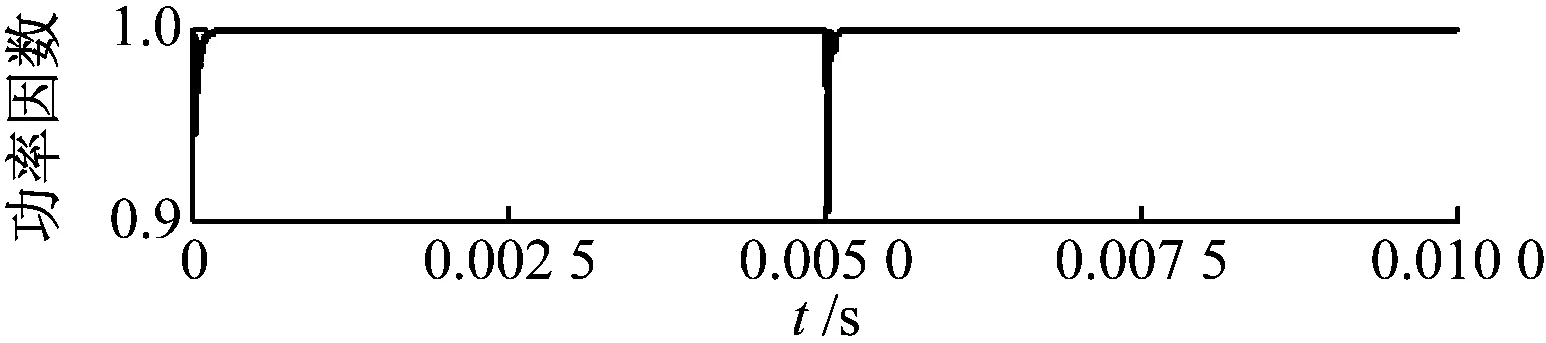
(b) 全谐振补偿方式下互感跃变
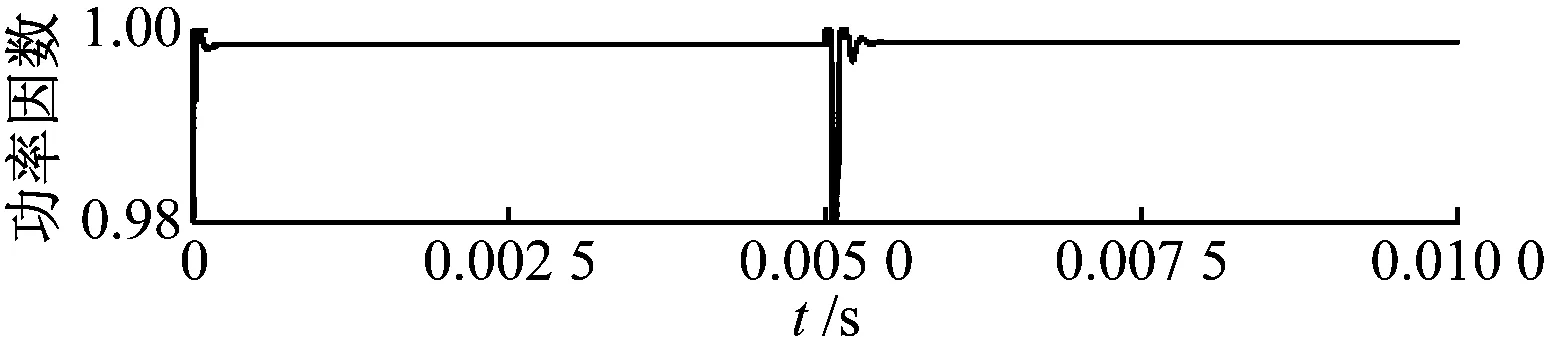
(c) 传统补偿方式下电阻负载跃变

(d) 全谐振补偿方式下电阻负载跃变
图6(a)、图6(b)为SP型补偿拓扑在t=0.005 s(t为时间),互感从系统谐振参数30 μH跃变到60 μH时,一次侧功率因数的变化。可发现重新稳定后,传统补偿方式下的功率因数降低,系统处于失谐状态;而全谐振补偿方式下由于谐振频率不受互感影响,系统功率因素波动后重新稳定于1,系统仍处于谐振状态。
图6(c)、图6(d)为SP型补偿拓扑在t=0.005 s电阻负载从系统谐振参数40 Ω跃变到90 Ω时,一次侧功率因数的变化。由于补偿电容计算忽略了内阻影响,传统补偿方式下一次侧补偿电容计算不精确,系统即使处于预设谐振参数(M=30 μH)下,系统功率因数仍不为1,但不受负载变化影响;全谐振补偿方式下由于电阻负载对系统谐振频率有影响,在电阻负载变化后,系统一次侧功率因数降低,系统处于失谐状态,说明电阻负载变化对系统谐振效果的影响较明显。
通过互感跃变验证了SP型MC-WPT系统在全谐振补偿方式下即使互感发生变化,也能快速趋于稳定。因此,SP型MC-WPT系统在煤矿井下受复杂因素如粉尘、振动等引起互感变化时,系统不受影响,因此SP型MC-WPT系统更适合应用于互感容易变化的煤矿井下,但仍然受电阻负载的影响较大。井下用电设备受复杂因素(如线路老化等)影响会引起负载电阻变化,需进一步改进,使系统脱离负载束缚,以适用于煤矿井下电阻负载多变的情况。
4 全谐振补偿方式的优化
针对二次侧并联型MC-WPT系统谐振频率受电阻负载影响及电阻负载具有下限值(需满足RL≥2ω0LS)的问题,利用DC-DC变换器,将阻抗匹配思想与有源功率因数校正思想相结合,实现系统整流桥输入侧等效阻抗始终等于预设谐振频率对应电阻值,同时保证系统整流桥输入电流与电压同相位,降低DC-DC变换器的引入对系统阻抗的影响。
采用四开关Buck-Boost变换器对二次侧并联MC-WPT系统全谐振补偿方式进行优化[23]。四开关Buck-Boost变换器拓扑结构如图7所示。变换器由4个功率开关管T1—T4及电感L和电容C构成。ICin为Buck-Boost变换器输入电流,VCin为四开关Buck-Boost变换器输入电压,VCout为四开关Buck-Boost变换器输出电压,ICL为电感电流。
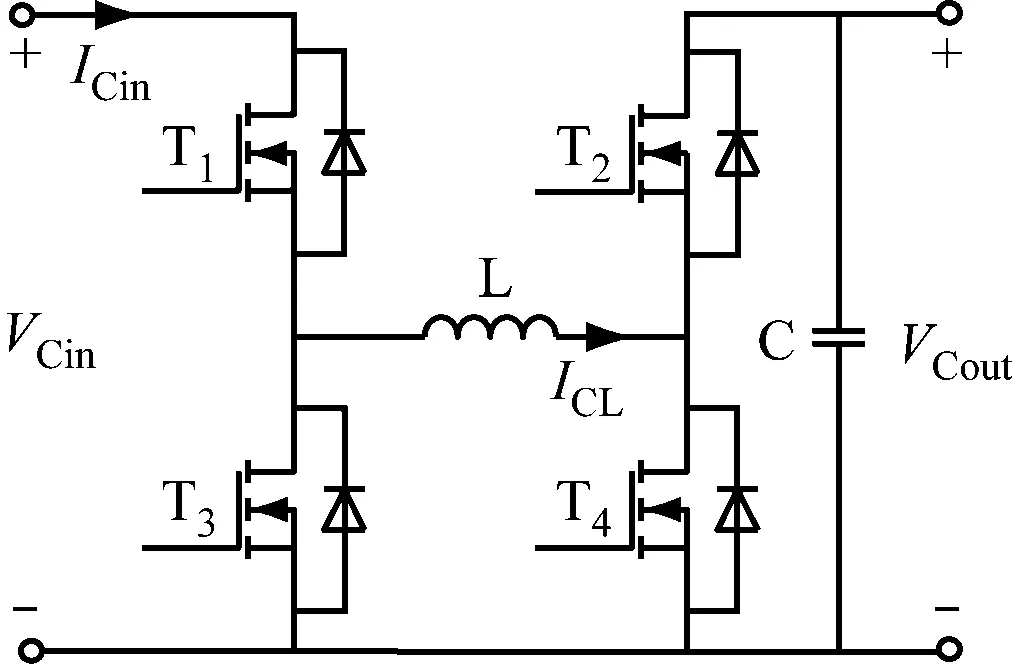
图7 四开关Buck-Boost变换器拓扑结构Fig.7 Four switch Buck-Boost converter topology
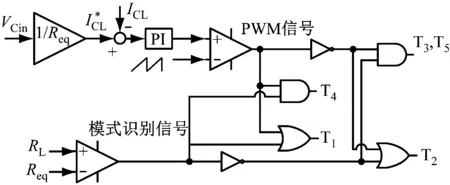
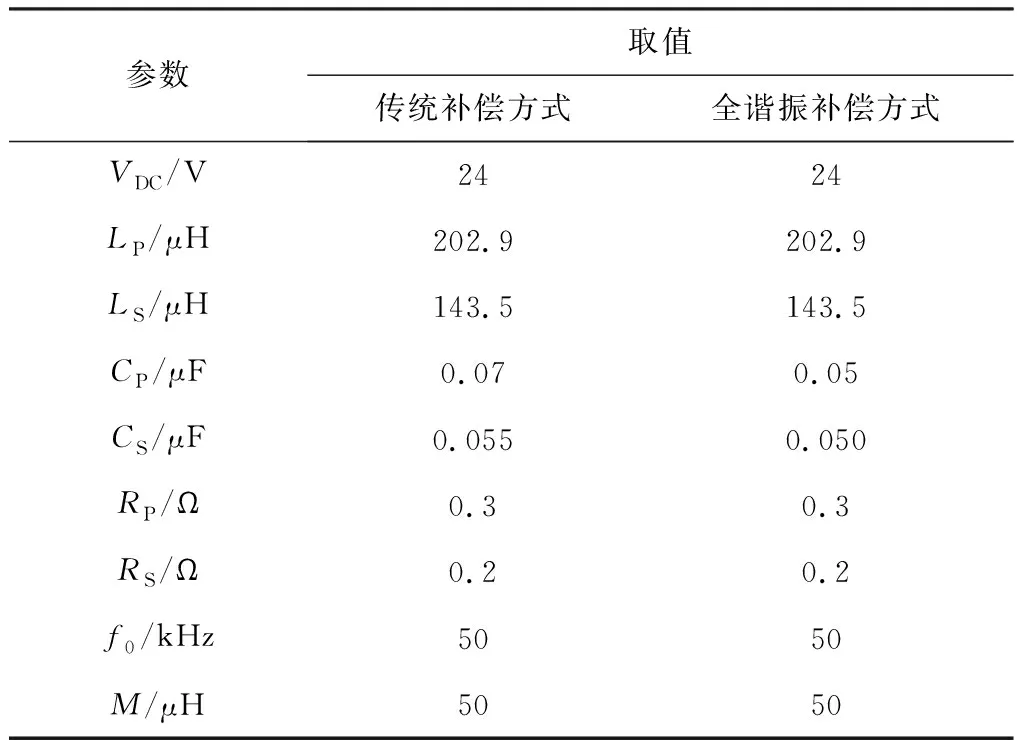
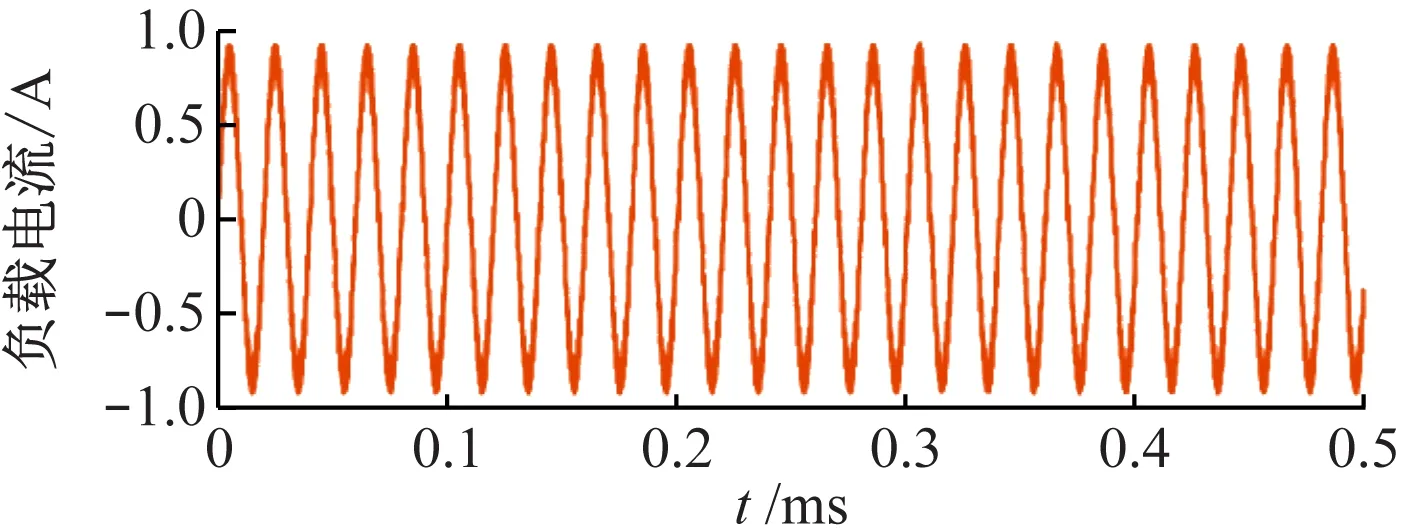
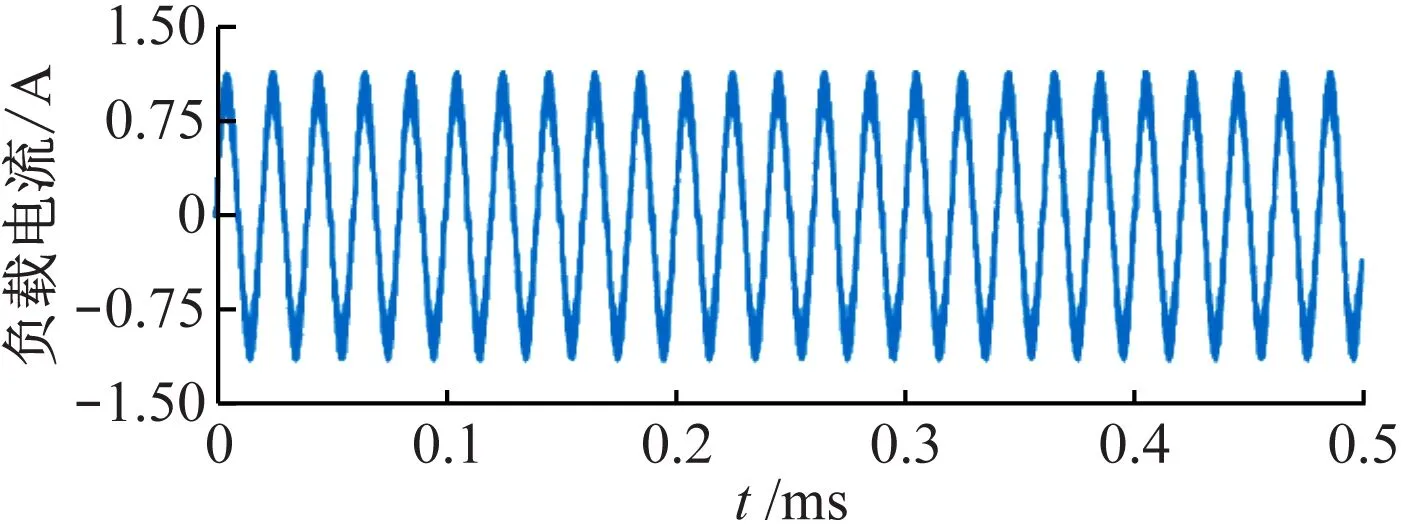
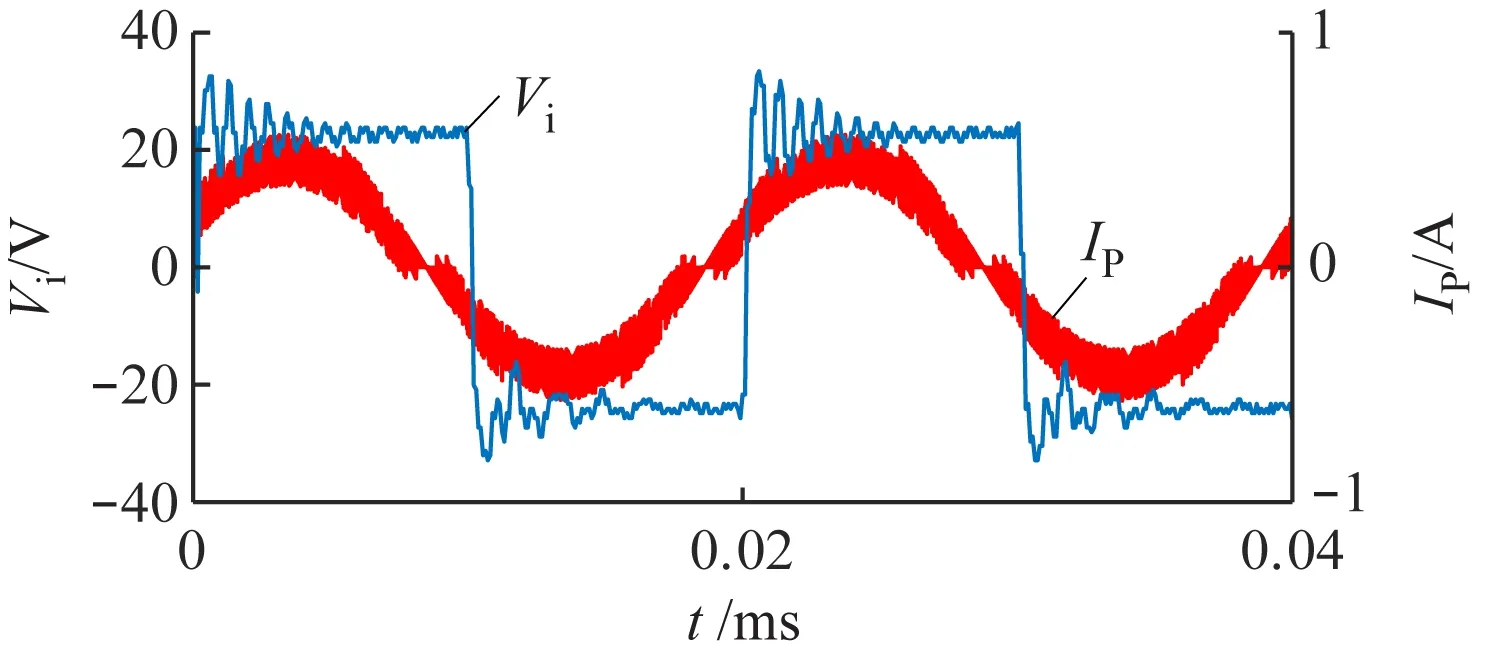
为降低系统损耗及共模干扰,采用双模态切换的控制方式,即当VCout>VCin时,T1常通,T3常断,T2与T4互补导通,四开关Buck-Boost变换器工作在Boost模式;当VCout 当四开关Buck-Boost变换器工作在Boost模式下,ICin连续时,ICin=ICL,系统可实现理想的阻抗匹配控制;工作在Buck模式下,ICin不连续,ICin≠ICL,MC-WPT系统难以实现阻抗匹配。针对此现象,引入补偿电阻R,通过对功率开关管T5的控制,可实现四开关Buck-Boost变换器在Buck模式下ICin连续,使二次侧并联MC-WPT系统在全谐振补偿方式下电阻负载可全范围调节。以SP型补偿拓扑为例,系统完整电路如图8所示,其中Req为整流桥输入侧等效电阻,R等于Req。当四开关Buck-Boost变换器工作在Boost模式下时,T5常断;当四开关Buck-Boost变换器工作在Buck模式下时,T3与T5同通断。故可得四开关Buck-Boost变换器阻抗匹配电路控制逻辑,如图9所示。 图8 系统完整电路Fig.8 Complete circuit diagram of the system 图9 阻抗匹配电路控制逻辑Fig.9 Impedance matching circuit control logic 为验证上述理论的正确性,利用Simulink搭建SP型MC-WPT系统,仿真参数:LP=202.642 μH,LS=144.2 μH,RP=0.4 Ω,RS=0.35 Ω,Req=100 Ω,VDC=24 V,CP=CS=0.05 μF,f0=50 kHz,M=50 μH。 不同电阻负载下SP型MC-WPT系统一次侧电压、电流仿真波形如图10所示。图10(a)和图10(c)为系统未接入阻抗匹配电路时的波形,当系统电阻负载偏离预设谐振参数(RL=100 Ω)时,系统一次侧电路明显失谐,电压与电流未同相;图10(b)和图10(d)为接入阻抗匹配电路后的波形,可看出经阻抗匹配后,即使电阻负载发生变化,一次侧电路仍处于谐振状态,一次侧电压、电流同相,说明二次侧电路也处于谐振状态。 为验证上述理论及仿真分析的正确性,以SP型MC-WPT系统为实验对象,搭建SP型MC-WPT实验系统,如图11所示。 图11 实验系统Fig.11 Experimental system 实验系统所用开关管均为IPP320N20N3,控制芯片采用STM32F103C8T6,开关管驱动器为IR2104,系统采用固定50 kHz逆变开关频率。实验系统参数见表1。RL=100 Ω时传统补偿方式与全谐振补偿方式下系统负载电流如图12所示。 通过图12计算得传统补偿方式下系统输出功率为37.93 W,全谐振补偿方式下系统输出功率为50.10 W,相较于传统补偿方式,全谐振补偿方式在同等参数条件下,将输出功率提升了25%左右。 系统从预设谐振参数M=50 μH变为M=90 μH后,一次侧电压、电流波形如图13所示,可看出在传统补偿方式下,互感变化后一次侧电压、电流有明显相位差,系统处于失谐状态,全谐振补偿方式下系统仍处于谐振状态。 表1 系统参数Table 1 System parameters (a) 传统补偿方式 (b) 全谐振补偿方式 (a) 传统补偿方式 (b) 全谐振补偿方式 全谐振补偿方式下电阻负载不同时系统一次侧电流与电压波形如图14所示。 图14(a)与图14(c)为系统未接入阻抗匹配电路时,一次侧电压与电流在不同电阻负载下的波形,可看出系统一次侧电压、电流不同相,RL=50 Ω 时,电压滞后于电流;RL=200 Ω 时,电压超前于电流。图14(b)与图14(d)为系统接入阻抗匹配电路后,在不同电阻负载下的一次侧电压、电流波形,可看出电压、电流无相位差,系统谐振效果较理想。 (a) RL=50 Ω (b) RL=50 Ω阻抗匹配 (c) RL=200 Ω (d) RL=200 Ω阻抗匹配 未加入及加入阻抗匹配电路时,系统一次侧电压、电流相位差(正值表示电压超前电流,负值表示电压滞后电流)随电阻负载的变化趋势如图15所示。 图15 一次侧电压、电流相位差Fig.15 Phase difference of primary side voltage and current 从图15可看出,系统经阻抗匹配后,一次侧电压、电流相位差不受电阻负载的影响,说明系统谐振状态不受影响,同时由于谐振补偿方式下互感不影响谐振频率,所以可采用固定逆变开关管频率的控制方式,保证系统始终谐振,简化了系统一次侧控制难度。上述实验证明本文设计的阻抗匹配电路可使二次侧并联MC-WPT系统在全谐振补偿方式下,在电阻负载全范围内均可实现系统处于谐振状态,摆脱了电阻负载对系统谐振频率的影响。 (1) 针对井下应用MC-WPT系统二次侧并联补偿结构时,传统补偿方式存在二次侧未谐振的问题,以SP型、PP型、LCC-P及LCL-P型补偿拓扑为例,在未添加任何元件的前提下,得到系统处于全谐振状态的参数约束关系,使一次侧、二次侧电路均处于谐振状态。 (2) 通过对比分析2种补偿方式的功率及效率,发现SP型、PP型及LCL-P型补偿拓扑在全谐振补偿方式下的功率均优于传统补偿方式下的功率,4种补偿拓扑在全谐振补偿方式下均可提高系统功率因数及功率密度,且全谐振补偿方式下的SP型拓扑不受互感影响。在全谐振补偿方式下,4种二次侧并联结构的MC-WPT系统无需提供无功功率,输出功率增加。通过互感与电阻负载跃变仿真,验证了SP型MC-WPT系统更适合应用于煤矿井下,在全谐振补偿方式下,即使受煤矿井下复杂因素影响造成系统互感跃变,也会快速趋于稳定,系统保持谐振。 (3) 对二次侧并联型MC-WPT系统提出了优化方案,并使用SP型拓扑为实验对象进行了验证,实验结果表明本文理论分析有效,SP型MC-WPT系统在全谐振补偿优化方式下能脱离电阻负载的束缚,系统不受互感影响及负载变化影响,稳定在全谐振状态下,提高了系统输出功率与输出效率,为煤矿井下应用二次侧并联型MC-WPT提供了理论依据。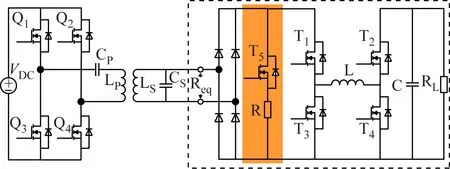

5 实验验证



6 结论

