高精度矿用超声波风速测量仪设计

李秉芮， 刘娜， 井上雅弘

(山东科技大学 安全与环境工程学院， 山东 青岛 266500)

0 引言

通风智能化是指通过动态采集通风信息实现通风状态分析、故障诊断和风量调控，是矿井通风的主流发展方向[1-2]。信息采集是通风智能化的基础，然而目前井下风速测量常用的机械式风表、压差式和超声波涡街式风速监测传感器的测量范围大多为0.3～15 m/s，误差为±0.2 m/s[3]，启动风速几乎都大于0.3 m/s[4-8]。《煤矿安全规程》第一百三十六条规定：输送机巷，采区进、回风巷，采煤工作面，掘进中的煤巷和半煤岩巷的最低允许风速为0.25 m/s；掘进中的岩巷和其他通风人行巷道的最低允许风速为0.15 m/s。现有风速传感器难以满足《煤矿安全规程》的风速测量要求，同时也难以满足通风系统异常诊断及智能调控的需要，是通风智能化需要解决的技术难题之一[9-10]。

超声波风速测量仪可以适应恶劣环境，具有较高的精度和较宽的测量范围，因而被广泛应用于气象、军事、矿山等领域[6,11-13]。利用超声波测风速有涡街法和时差法2种技术途径。之前煤矿普遍使用的超声波风速传感器多采用涡街法，如GFW15型矿用风速传感器[5]，但涡街法对风流稳定性及安装精度要求较高。时差法不破坏风流流场，无压力损失，几乎不受风流温度、压力等因素影响，是未来矿井风速测量技术的发展方向。国外生产的风流监测设备如Accutron MAQS和Zephyr AQSTM均采用超声波时差法。国内早期开发的基于超声波时差法的矿用风速测量仪使用2对超声波换能器，通过交替发射与接收超声波信号实现风速测量[14]。文献[15]在此基础上进行了改进，使用1对超声波换能器完成风速测量，最低测量风速达0.2 m/s，性能优于传统的风速测量仪，但由于风速越低，测量误差越大，该风速测量仪仍不能满足矿井低风速条件下精准测风需要。针对该问题，本文基于超声波时差法风速测量原理，设计了一种具有低启动风速的高精度矿用超声波风速测量仪。

1 超声波时差法风速测量原理

超声波在空气中的传播速度与风速叠加，在顺风方向上传播速度加快，在逆风方向上传播速度变慢，在一定检测条件下与风速函数对应，可通过计算求出精确风速。超声波在空气中的传播速度受温度的影响，但若采用2个通道分别检测2个相反方向的超声波传播速度，则温度对超声波传播速度产生的影响可以忽略不计。超声波时差法风速测量原理如图1所示。在巷道相对的两侧巷壁分别布置A1，A2和B1，B22组超声波探头。其中A1，B2为超声波发射探头，A2，B1为超声波接收探头。发射探头与接收探头的距离为L，其连线与风流方向的夹角为α。

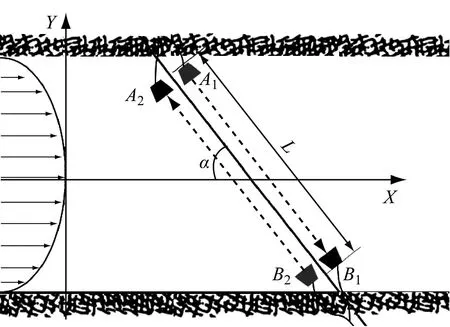
图1 超声波时差法风速测量原理Fig.1 Principle of wind speed measurement of ultrasonic time-difference method

设巷道的风流方向为X方向(巷道轴方向)，与风流方向垂直的方向为Y方向，沿Y方向的风速分布为v(Y),当A1，B2同时发射超声波时，顺风方向超声波由A1到B1的传播时间为

(1)

式中:C为巷道空气中超声波的传播速度，m/s，C=331.45+0.607t,t为巷道空气温度，℃;l为测距的积分变量。

逆风方向由B2到A2的传播时间为

(2)

用平均风速vm表示沿Y方向的风速分布v(Y)，并代入式(1)和式(2)得

(3)

(4)

由式(3)和式(4)可得

(5)

(6)

当L已知时，测量顺风与逆风状态超声波的传播时间，根据式(5)即可求出沿Y方向的平均风速，且与风流温度无关。当超声波探头受外界影响而发生位移时，可根据式(6)计算位移量并校准探头间距。

2 超声波风速测量仪设计和信号调理

2.1 超声波风速测量仪设计

超声波风速测量仪工作原理如图2所示。超声波发射探头A1，B2和接收探头A2，B1交错设置，形成2个超声波传播通路，分别用于测算超声波在特定风速场中的顺风和逆风传播时间。

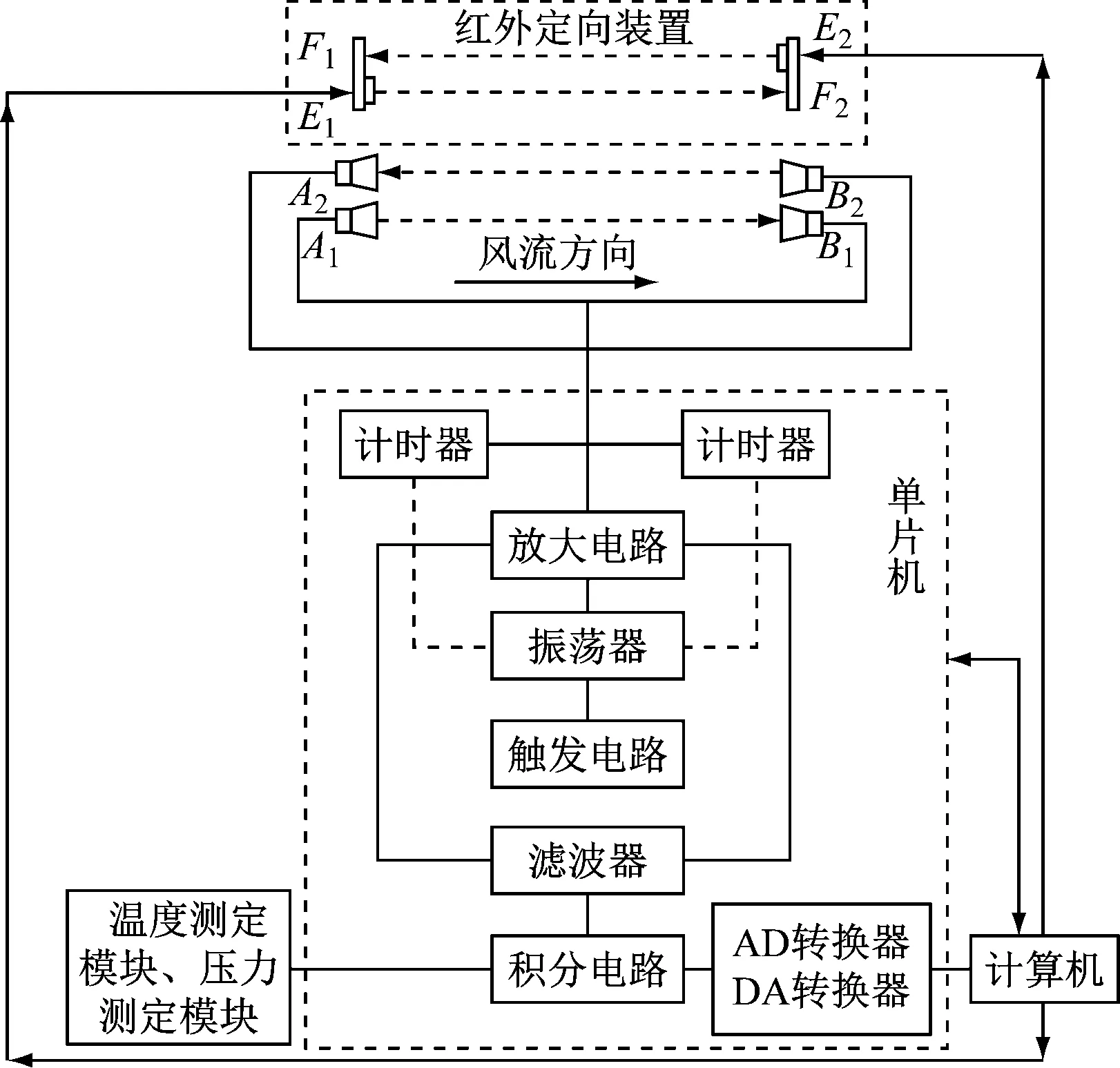
图2 超声波风速测量仪工作原理Fig.2 Working principle of ultrasonic anemometer

风速测量仪由单片机、超声波收发模块及红外定向装置等组成。单片机集放大电路、计时器、振荡器、触发电路、滤波器、积分电路、信号转换器于一体，完成时差法风速测量。红外定向装置由红外线发射器E1，E2及标志区F1，F2组成，位于超声波探头A2，B2上方。E1，E2分别发射红外线至对面标志区F1，F2，进行风速测量仪安装方向校准，以减小由安装方向偏离引起的测量误差。

风速测量仪工作电压为5 V，通过触发电路触发振荡器，产生具有一定频率的脉冲信号，激励超声波发射探头发射规定频率的超声波，即将电信号转换为超声波信号。在发射超声波的同时，单片机启动计时器。2个超声波接收探头接收超声波信号，并将其转换为电信号输入单片机，同时中断计时器。信号经过放大、滤波处理后，再经过积分电路处理成方波。低电平持续时间就是超声波在空气中的传播时间，在顺风与逆风条件下低电平持续时间不同，由此可计算出超声波传播时差，根据式(5) 可计算出风速并判断风向，然后实时输出风速。

2.2 超声波信号调理

超声波信号调理是指对超声波信号进行与或非逻辑运算。对振荡器产生的电信号进行信号处理及门电路运算，得到传播时间差造成的脉冲宽度，再通过滤波器及积分电路将电信号转换为稳定的输出电压。

超声波风速测量仪信号调理如图3所示。超声波风速测量仪由IO口输出一个10 μs的高电平信号至TRIG(控制端)，激励超声波发射探头A1，B2发射8个40 kHz方波(波形O)，同时A1和B2的TRIG输出一个低电平。B1接收到A1发射的超声波后，换能器产生脉冲信号a，同时发生电平跳变，从B1的ECHO(接收端)输出一个高电平，经积分电路整形为方波(波形P)并存储，低电平宽度为超声波在顺风条件下的传播时间T1。A2接收到B2发射的超声波后，换能器产生脉冲信号b，同时发生电平跳变，从A2的ECHO输出一个高电平，经积分电路整形为方波(波形Q)并存储, 低电平宽度为超声波在逆风条件下的传播时间T2。图3中，Tr为超声波风速测量仪的1个发射周期，即从超声波发射探头A1，B2第1次发射8个40 kHz方波到第2次发射方波的时间；T0为待机时间，即超声波发射探头发射8个40 kHz方波后至下一次发射的等待时间。

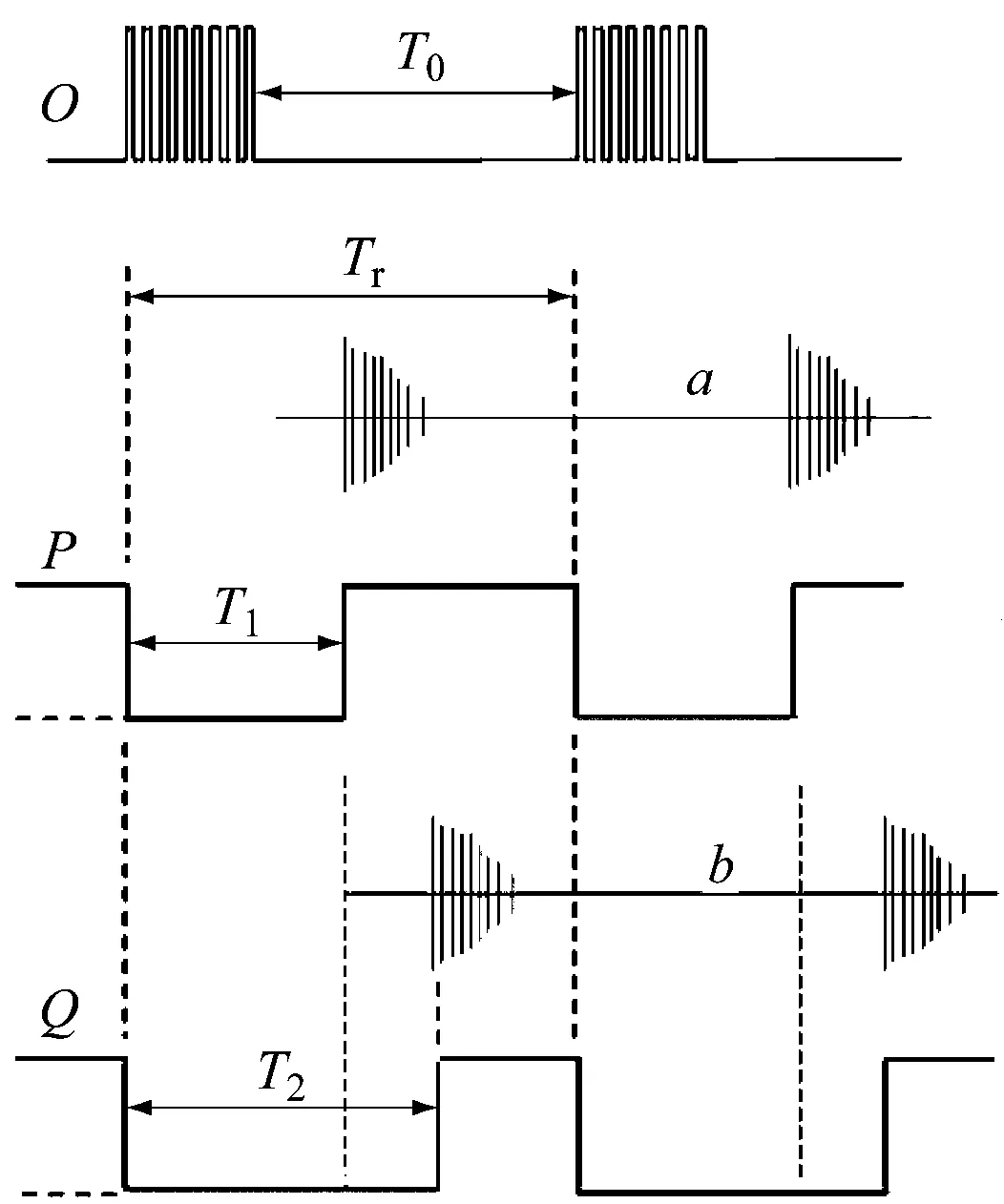
图3 超声波风速测量仪信号调理Fig.3 Signal conditioning of ultrasonic anemometer

3 性能参数设定及其影响因素分析

超声波风速测量仪的测量精度除了受频率、待机时间等性能参数影响外，还受探头方向、声噪声等因素干扰。

3.1 超声波频率

超声波在空气中传播的过程中，强度会随距离增大而衰减，频率越高，衰减率越大，长距离测量越困难；但低频超声波的工作噪声较大，易对测量精度产生影响。按照图1所示的超声波风速测量仪布置方式，10 m以内的测距基本可以满足井下巷道测风要求。根据理论和实践经验，10 m以内测距最适宜的超声波频率为40 kHz[16]，因此，本文选用特性频率为40 kHz的超声波换能器。

3.2 待机时间

若超声波风速测量仪待机时间过短，则测量空间内发射探头的余振、回响信号等声噪声会降低测量精度；若待机时间过长，则测量响应速度慢。因此，需设置合理的待机时间。设探头间距L=10 m，α=0，空气温度t=0 ℃，巷道平均风速vm=10 m/s，考虑反射波的影响，超声波从发射到返回所需的传播时间为

(7)

由式(7)可知，待机时间大于60 ms时，可避免反射波的影响。若探头间距L=1 m，则待机时间应大于6 ms。

设定探头间距L=1 m，待机时间分别为50，100，200 ms，连续进行300次测试，风速标准差及风速波动范围见表1。可以看出，当待机时间大于超声波折返所需传播时间时，风速标准差很小，实测值波动小，表明测量稳定性好，几乎不受待机时间的影响。考虑风速测量仪的响应速度，设定待机时间为100 ms。

表1 不同待机时间的风速标准差及波动范围Table 1 Standard deviation and fluctuation range of wind speed under different stand-by time

3.3 超声波探头方向性

超声波具有良好的方向性，超声波场中至波源充分远处同一横截面上各点的声压不同，轴线上的声压最高[17]。一般实用性的超声波探头半扩散角为4～15°，即测距为1 m时，超声波探头方向的最大允许错位为0.268 m。因此，设超声波探头方向错位0.25 m，采用4种布置方式进行室内实验，如图4所示。超声波连续发射100次。

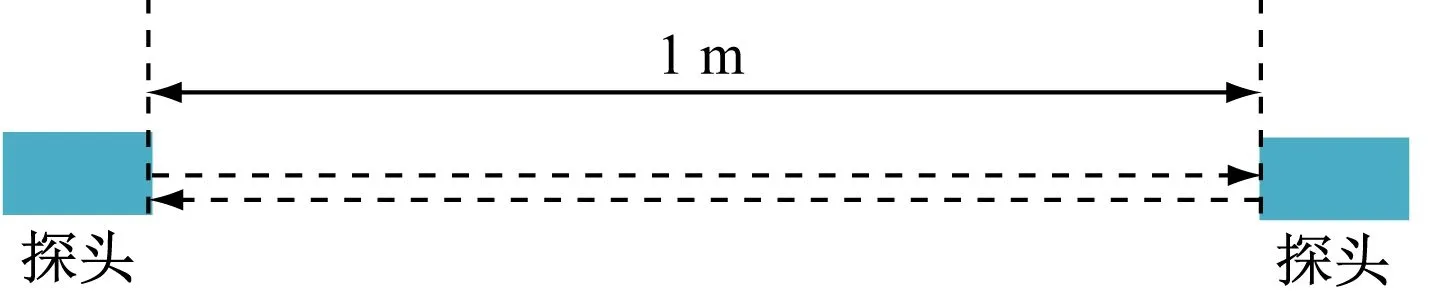
(a) 布置方式1

(b) 布置方式2

(c) 布置方式3

(d) 布置方式4

不同超声波探头布置方式的实测风速如图5所示，风速标准差及波动范围见表2。

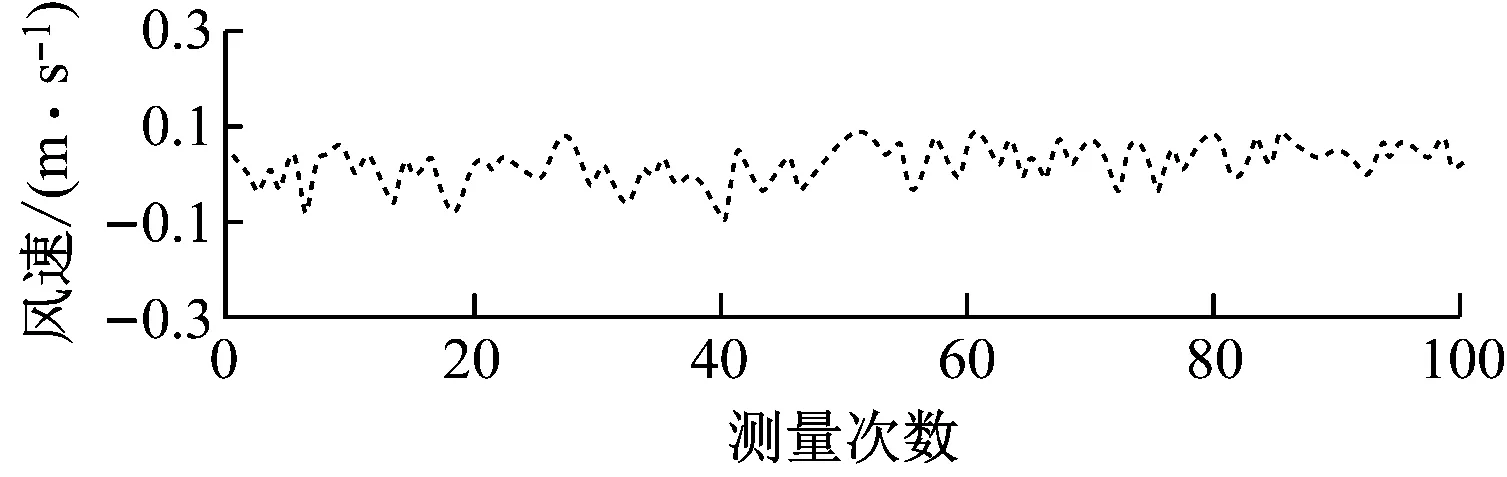
(a) 布置方式1实测风速

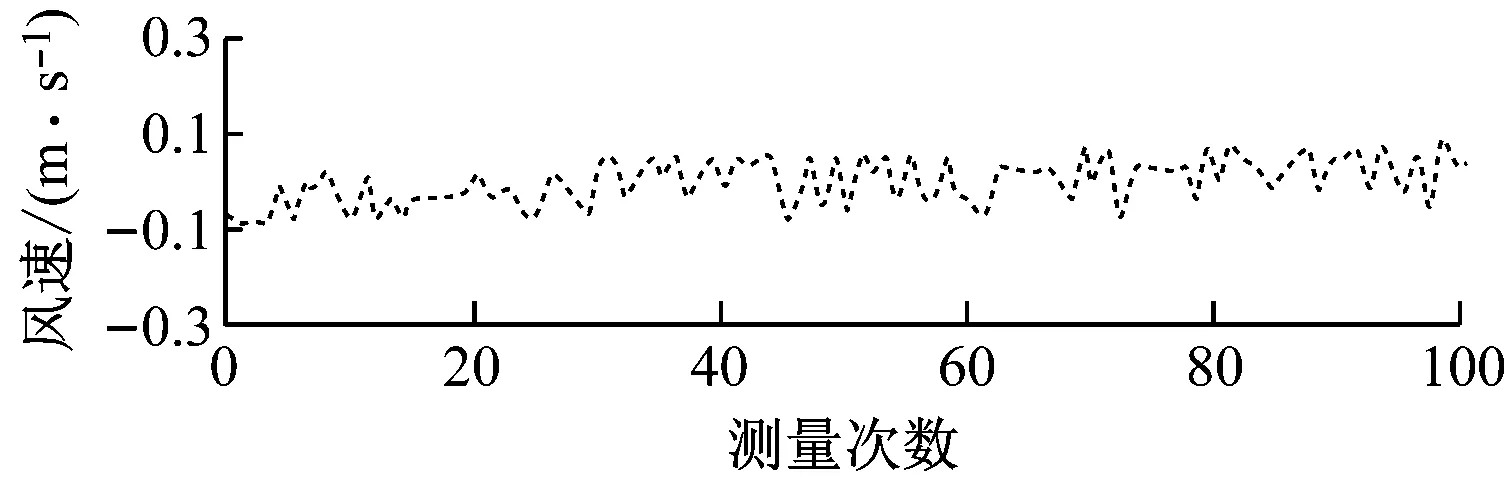
(b) 布置方式2实测风速

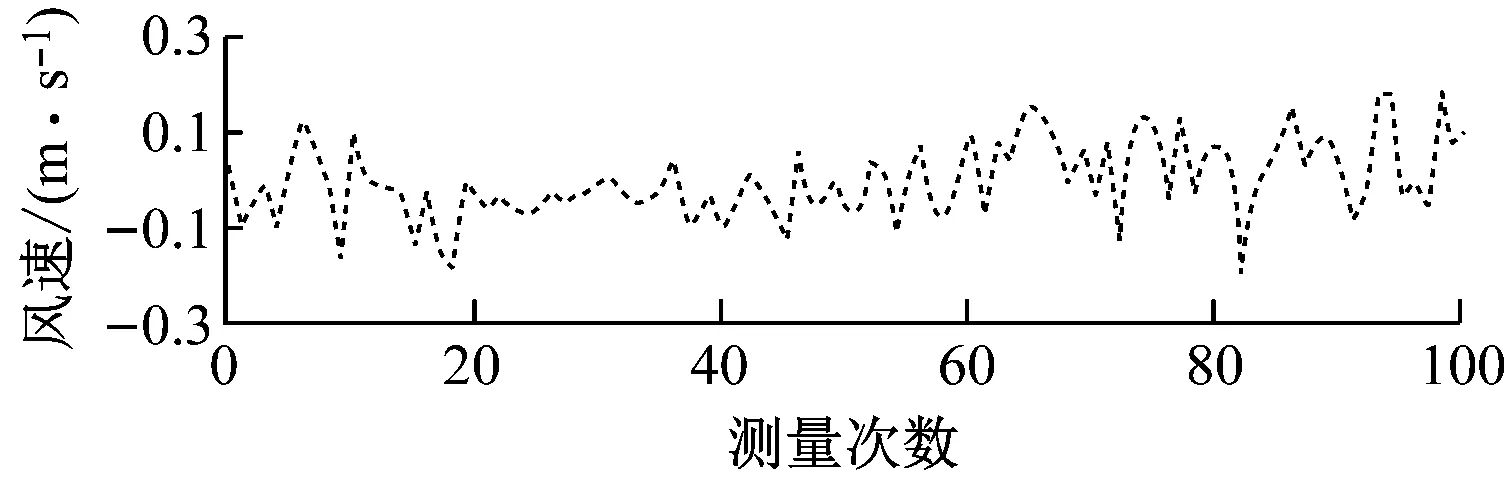
(c) 布置方式3实测风速

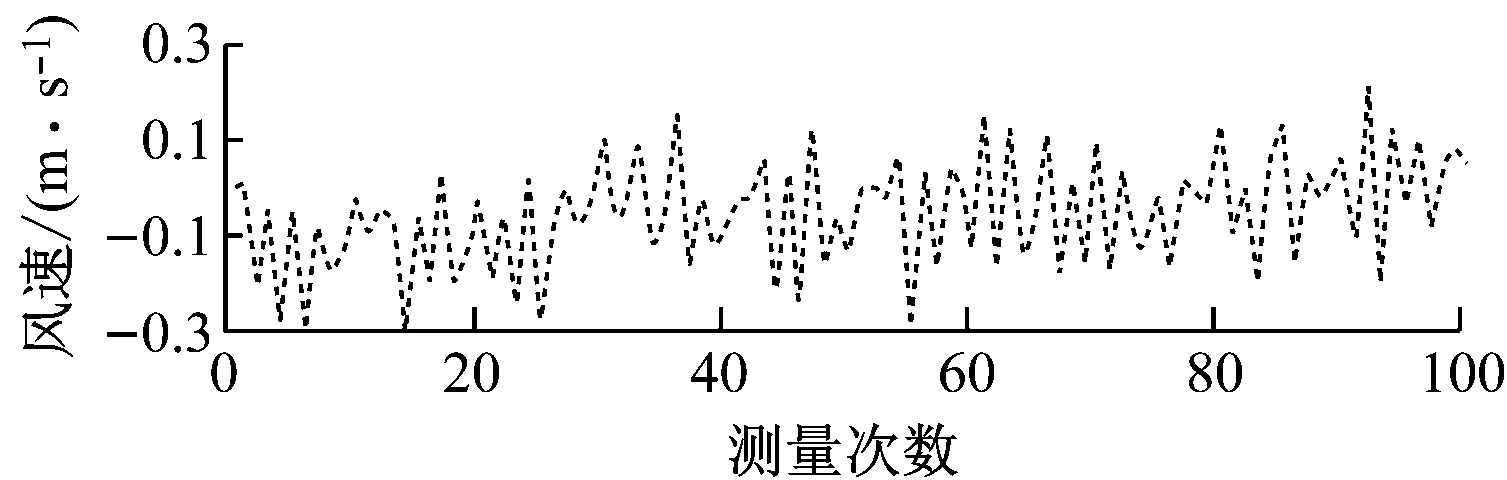
(d) 布置方式4实测风速

从图5和表2可看出，超声波探头方向错位越严重，风速标准差和波动范围越大，表明探头方向对测量的准确性与可靠性有一定影响。为减小探头方向错位造成的误差，本超声波风速测量仪设置了红外定向装置。

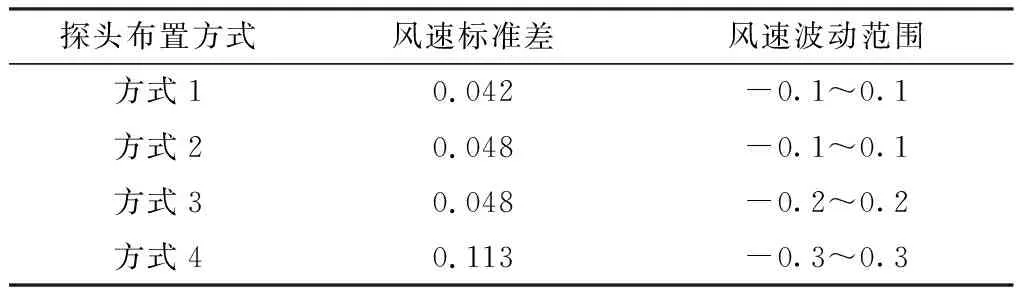
表2 不同超声波探头布置方式的风速标准差及波动范围Table 2 Standard deviation and fluctuation range of wind speed under different ultrasonic probe arrangements m/s

3.4 数据平滑处理

对原始风速波形曲线进行平滑处理的目的是消除随机噪声，提高输出风速的稳定性。通过比较分析，本文选用滑动平均法，其原理是对n个非平稳数据{yi}(i=0,1,…,n-1)，逐个滑动取m个相邻数据计算算术平均值：

(8)

式中：fk为第k个算术平均值；yk+i为原始风速测量值。

m的取值直接影响平滑效果:m值较大有利于抑制频繁随机起伏的随机误差，但可能导致高频变化的确定性成分被平均；m值较小不利于抑制随机误差。数据处理中多设置m值为5～11。为确认m值对风速波形曲线平滑效果的影响，分别取m值为4，6，8，10，12，对测距1.0 m的原始风速波形进行数据平滑处理，结果如图6所示。

(a) 原始风速波形

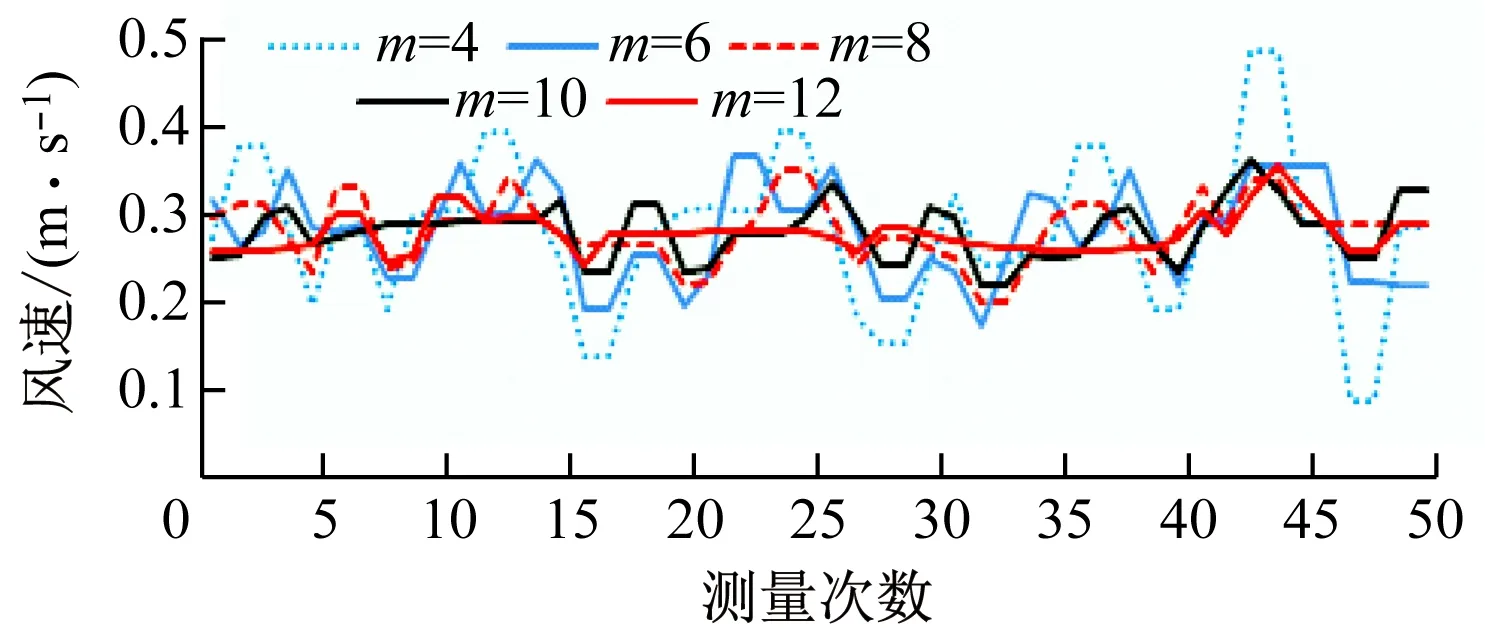
(b) 平滑处理后波形

m值与风速标准差的关系如图7所示。可以看出，m值越大，风速标准差越小，风速变化范围越小，风速越稳定，但风速测量仪响应速度变慢。当m≥8时，风速标准差变化小，可以认为m对风速平均值的影响很小，因此，本文取m=8进行数据平滑处理。

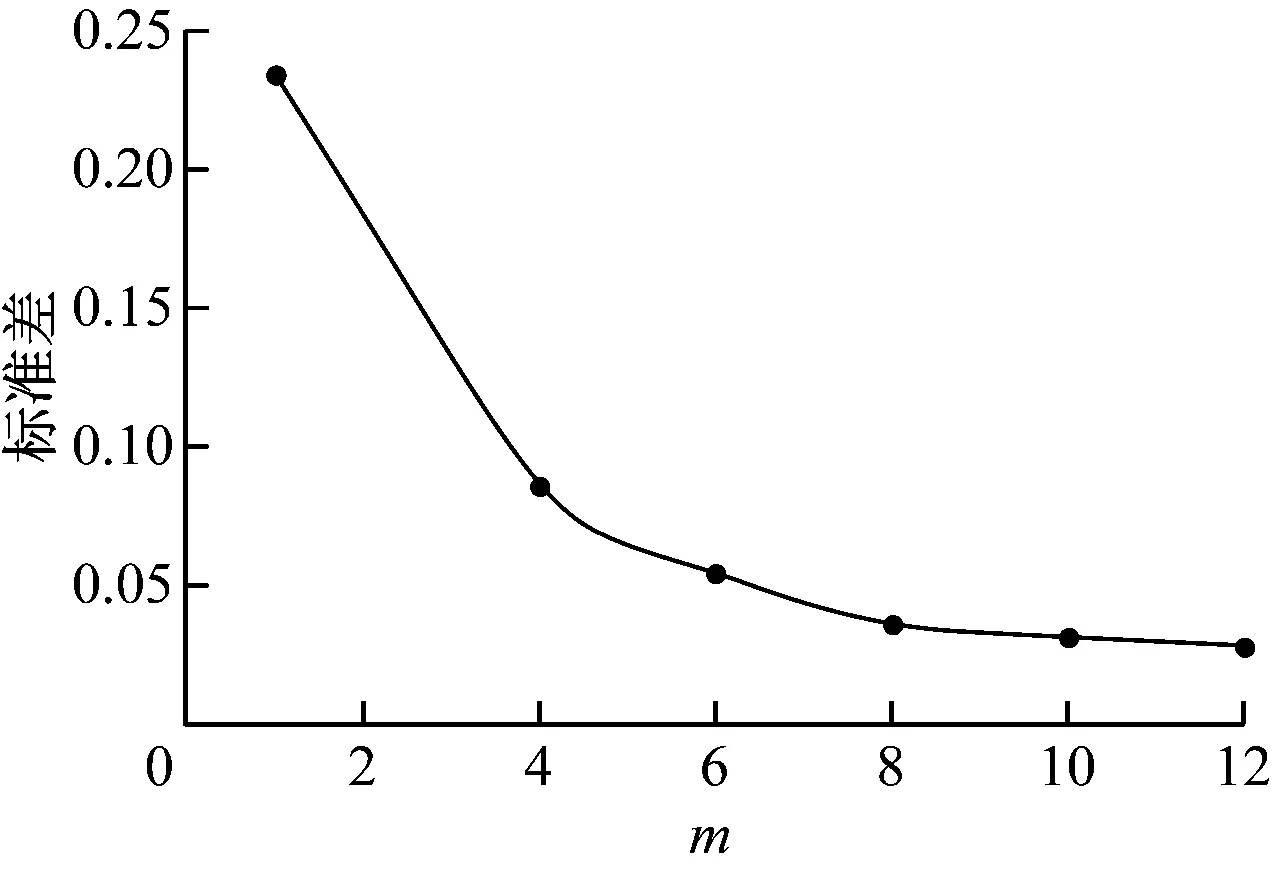
图7 m值与风速标准差的关系Fig.7 Relation between m and the standard deviation of wind speed

4 性能指标分析

(1) 分辨率。设α=0，对式(5)求T1的导数，得

(9)

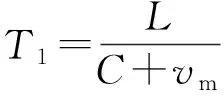
(10)

已知超声波风速测量仪计时器的分辨率为1 μs，设L=5 m，C=340 m/s，vm=5 m/s，代入式(10)得dvm=0.011 9 m/s，即超声波风速测量仪的测量分辨率为0.01 m/s。

(2) 测量误差。已知超声波探头的测距误差|dl|≤3 mm，换算为超声波传播时间误差得

(11)

将dT1代入式(10)得dvm=0.103 m/s，则超声波风速测量仪误差为0.1 m/s。

(3) 启动风速。因为采用非机械式传动方式，理论上超声波风速测量仪的启动风速应该等于其分辨率。根据实验室内无风、微风状态的实测，在风速小于0.1 m/s的情况下，超声波风速测量仪均获得了稳定的实测值，证明其启动风速低于0.1 m/s。

5 结论

(1) 基于超声波时差法风速测量原理，设计了具有低启动风速的高精度矿用超声波风速测量仪。通过2个发射探头同时发射超声波，形成2个超声波传播通路，温度对风速测量的影响可以忽略不计。

(2) 采用红外定向装置，可减小超声波探头方向错位引起的测量误差。选用滑动平均法对原始风速波形曲线进行平滑处理，以消除随机噪声，提高输出风速的稳定性。

(3) 理论计算和实验结果表明：该风速测量仪的分辨率为0.01 m/s，测量误差为±0.1 m/s，启动风速低于0.1 m/s，可以满足矿井低风速条件下的精准测风要求，今后将通过实践进行进一步验证。