矿井带式输送机运行状态预测方法
李敬兆, 孙杰臣, 叶桐舟
(1.安徽理工大学 电气与信息工程学院, 安徽 淮南 232001; 2.安徽理工大学 机械工程学院, 安徽 淮南 232001)
0 引言
矿井带式输送机具有运输效率高、输送距离长等优势,一旦发生故障会严重影响煤矿生产安全和工作效率[1]。目前,通过在带式输送机重要零部件部署相关传感器,能够得到带式输送机运行状态[2-3]。然而,这种方式只能实现事后维护,无法满足带式输送机预知维修的要求。
近年来,矿井带式输送机运行状态预测逐渐成为研究热点,传感器监测数据结合神经网络预测模型是带式输送机运行状态预测的主流方法[4-5]。方宇[6]根据带式输送机常见故障类型对应的监测数值变化,利用主成分分析提取故障特征,然后利用灰狼算法优化的支持向量机对不同故障类型数据进行预测,从而实现带式输送机故障预警;高伟[7]通过分析当前带式输送机监控系统中软硬件数据随运行时间的变化规律,利用循环神经网络对数据进行预测,从而得到带式输送机运行状态信息。Li Xiangong等[8]对带式输送机上各类传感器监测数据进行处理,并采用深度置信网络建立了带式输送机运行状态预测和性能评估模型。然而,利用接触式传感器对带式输送机运行状态进行监测存在安装不便、数据误差大等问题,导致带式输送机运行状态预测精度不高。
带式输送机不同运行状态下的音频信号存在一定差异。带式输送机正常运行时,当前时刻采集的带式输送机音频信号与前一段时间的音频信号相差不大;带式输送机发生撕裂、跑偏故障时的音频信号相较于正常运行时的音频信号有明显区别[9]。此外,音频信号由非接触式传感器采集,保证了数据的准确性。因此,本文提取带式输送机运行时的音频信号的梅尔频率倒谱系数(Mel-Frequency Cepstral Coefficients,MFCC)特征,使用残差块优化的卷积神经网络结合长短期记忆网络(Residual Block optimized Convolutional Neural Network combined with Long Short-Term Memory,Res-CNN-LSTM)模型对带式输送机运行状态进行在线预测。
1 矿井带式输送机运行状态预测流程
矿井带式输送机运行状态预测流程如图1所示。首先,对带式输送机运行时的原始音频信号进行滤波降噪处理,提取音频信号的MFCC特征;然后,将MFCC第1维分量(MFCC0)输入到Res-CNN-LSTM模型中进行离线训练;最后,将带式输送机实时音频信号特征输入到训练好的Res-CNN-LSTM预测模型中进行在线预测,得到带式输送机运行状态预测结果。
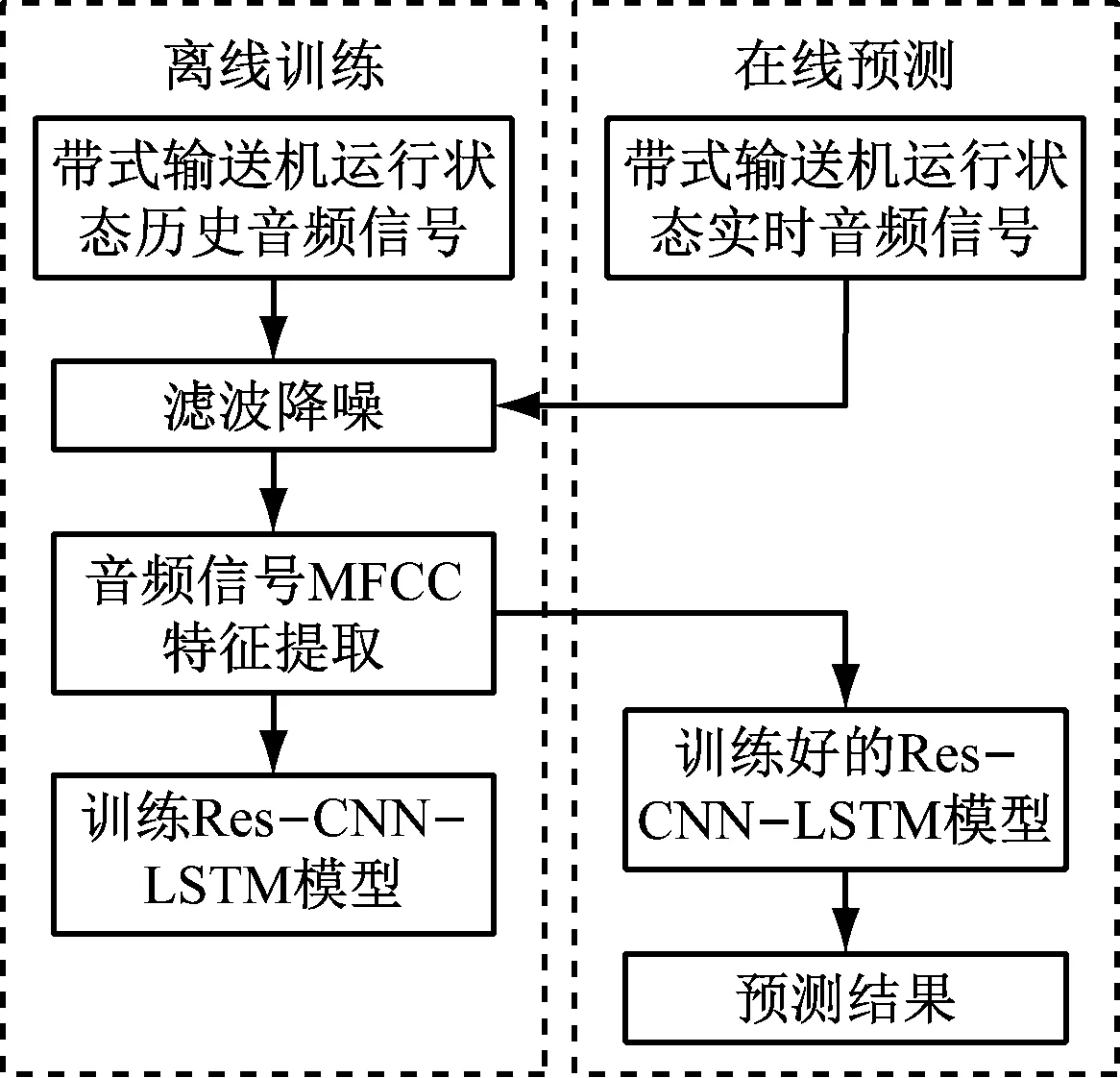
图1 矿井带式输送机运行状态预测流程Fig.1 Operation state prediction process of mine belt conveyor
2 音频信号特征提取
带式输送机工作环境复杂,采集到的原始音频信号中包含大量噪声。针对音频信号中噪声特点,采用高通滤波器滤除音频信号中低频噪声,再利用Boll谱减法进行整体噪声滤除。
MFCC作为语音信号中常用的时频域特征,已广泛应用于机械设备音频信号处理中[10]。但直接提取带式输送机音频信号的MFCC特征,得到的是高维特征数据,且大部分高维特征数据包含的设备运行状态信息少,不利于带式输送机运行状态预测。
MFCC第1维分量MFCC0包含的带式输送机音频信号特征最多,相对于其他维度分量具有较强的特征表达能力。为减少运行状态预测模型的输入数据量,将MFCC0作为带式输送机音频信号特征。MFCC0提取过程如图2所示,具体步骤如下。
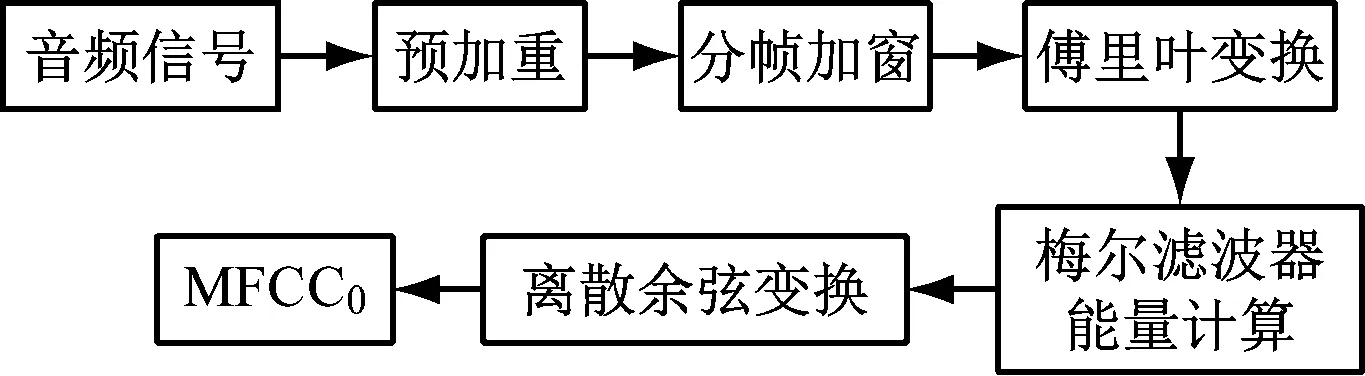
图2 MFCC0提取过程Fig.2 MFCC0 extraction process
(1) 滤波降噪后的带式输送机音频信号z(t)经过预加重可提高音频信号中的高频分量,弥补信号处理过程中的高频信息损失。
(2) 非平稳信号在很短的时间内可认为是线性信号,因此将音频信号分为若干帧,并对每一帧进行加窗处理,以避免频谱泄漏问题。
yn(t)=w(t)z((n-1)s+l)
(1)
式中:yn(t)为第n(1≤n≤N,N为音频信号总帧数)帧音频信号加窗后的结果;w(t)为汉明窗函数;s为帧移长度;l为帧长。
(3) 对每一帧音频信号进行快速傅里叶变换(Fast Fourier Transform,FFT),求取每一帧音频信号的频域值:
X(n,k)=FFT[yn(t)]
(2)
式中k为频域中谱线序号,0≤k≤K-1,K为总谱线数。
(4) 计算每一帧音频信号的能量谱:
E(n,k)=X2(n,k)
(3)
(5) 将每一帧音频信号的能量谱映射到梅尔滤波器,并与梅尔滤波器的频域响应相乘后求和,得到梅尔滤波器能量:
(4)
式中:m为梅尔滤波器序号,1≤m≤M,M为梅尔滤波器总数;Hm(k)为第m个梅尔滤波器频域响应。
(6) 对梅尔滤波器能量取对数后进行离散余弦变换,去除数据的相关性并实现数据降维,得到音频信号的MFCC:
(5)
式中j为离散余弦变换后的谱线。
(7) 保留第1个梅尔滤波器的MFCC,并去除前2帧的数据,然后取每一帧音频信号MFCC的第1个数,组成新的音频信号特征MFCC0。
3 Res-CNN-LSTM模型设计
Res-CNN-LSTM模型结构如图3所示。采用添加残差块的CNN自适应提取带式输送机音频信号的MFCC0的空间特征,并对数据进行降维;基于LSTM提取降维数据的时间特征,从而对带式输送机运行状态进行预测。
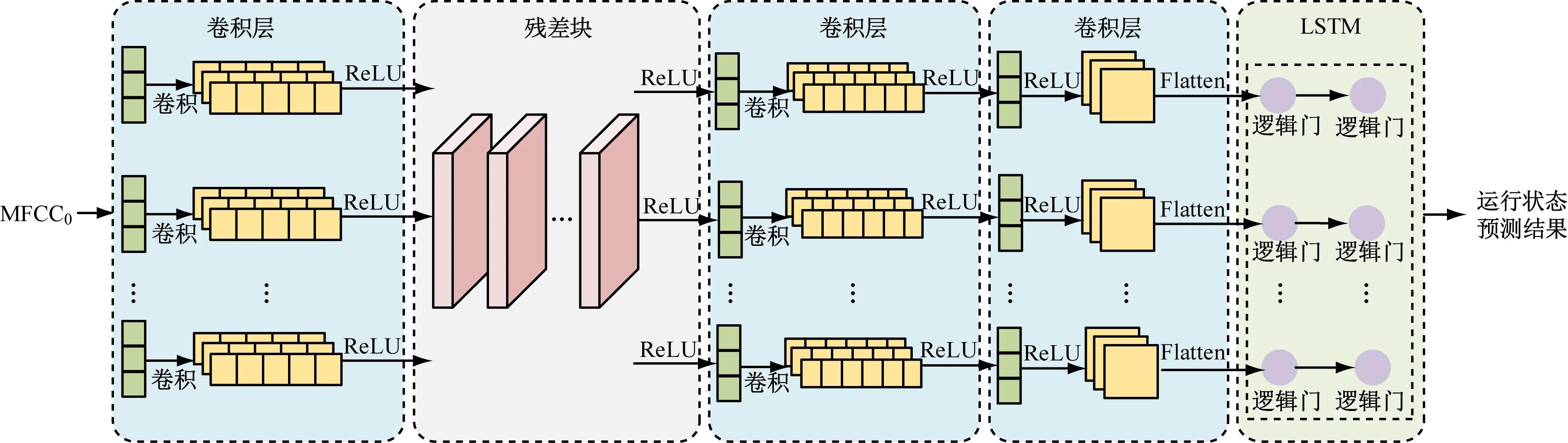
图3 Res-CNN-LSTM模型结构Fig.3 Structure of Res-CNN-LSTM model
3.1 残差块优化的CNN
CNN由卷积层、池化层和全连接层组成。卷积层通过卷积核对MFCC0进行卷积运算,提取MFCC0的空间特征;池化层用于对卷积层输出数据进行降维,仅保留较为明显的特征信息;全连接层用于对池化层输出结果进行运算,从而对特征进行分类[11-12]。传统CNN中的池化层虽然能够实现数据降维,但同时导致大量特征信息丢失。本文通过增加卷积层数量,采用不同尺寸卷积核对MFCC0进行卷积运算,得到较多的MFCC0空间特征。使用尺寸为1的卷积核构成的卷积层代替池化层进行特征降维,以避免池化后信息的丢失。考虑到卷积层数量增加会导致模型预测速度慢及过拟合现象,使用残差块对CNN进行优化。残差块结构如图4所示。图中BN为批归一化,ReLU为激活函数。
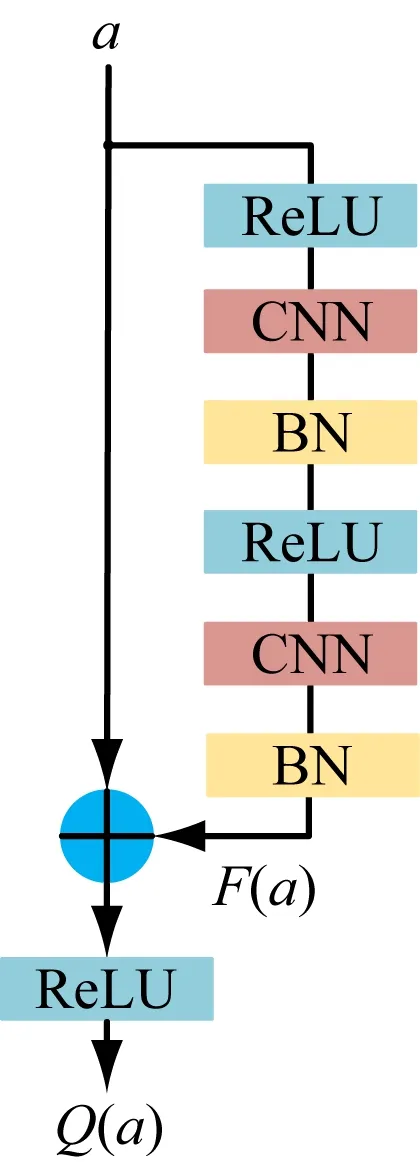
图4 残差块结构Fig.4 Structure of residual block
设输入为a时得到的特征为Q(a),则1个残差块可以表示为
Q(a)=a+F(a)
(6)
式中F(a)为残差部分。
3.2 LSTM
LSTM通过引入门控结构来控制信息的传递量和传递路径,有效记忆时序数据间的特征,充分挖掘MFCC0的时间特征,使预测结果更可靠。LSTM主要包括遗忘门、输入门和输出门[13-14],如图5所示。
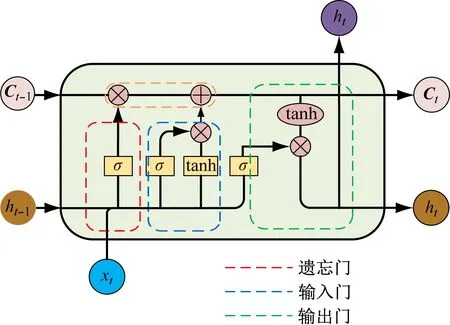
图5 LSTM结构Fig.5 Structure of LSTM
(1) 遗忘门:用于对上一时刻的输出信息进行选择性遗忘,保留与预测结果相关性大的信息。
ft=σ(Wf*[ht-1,xt]+bf)
(7)
式中:ft为遗忘门的输出值;σ()为sigmoid激活函数,取值范围为0~1,0代表遗忘信息,1代表保留信息;Wf为权重;*为卷积符号;ht-1为上一时刻LSTM输出;xt为当前时刻LSTM输入;bf为遗忘门的偏置。
(2) 输入门:将当前时刻的输入与上一时刻的输出共同作为输入门的输入,经过激活函数运算后结合前一个单元的候选向量,得到当前单元的候选向量,代替输入门上一时刻的状态。
it=σ(Wi*[ht-1,xt]+bi)
(8)
Ct=ftCt-1+ittanh(Wc*[ht-1,xt]+bc)
(9)
式中:it为输入门的输出值;Wi,Wc分别为输入门、候选向量的权重;bi,bc分别为输入门、候选向量的偏置;Ct为当前单元的候选向量;Ct-1为前一个单元的候选向量。
(3) 输出门:由sigmoid激活函数和tanh激活函数共同确定LSTM的最终输出ht。
ht=σ(Wh*[ht-1,xt]+bh)tanhCt
(10)
式中Wh,bh分别为输出门的权重和偏置。
4 实验与结果分析
对煤矿井下相似工作环境下同类型带式输送机运行时的音频信号进行采集,当传感器检测到带式输送机发生撕裂和跑偏故障时,追溯故障发生前24 h内的音频信号。长期实验中共采集到4次撕裂故障音频信号(共96 h)、5次跑偏故障音频信号(共120 h)。考虑到预测的动态性,以当前时刻及过去270 min的数据预测未来30 min的数据。
实验平台参数:CPU为Intel Core i7-10700;GPU为RTX2070;运行内存为32 GB;音频信号处理软件为Matlab 2018b;模型框架为PyTorch。
4.1 模型训练流程
Res-CNN-LSTM模型训练流程如图6所示,具体步骤如下:① 对带式输送机不同运行状态的音频信号提取MFCC0特征,并进行归一化处理;② 采用滑动窗口法[15]对不同运行状态的MFCC0特征数据进行分割;③ 寻找模型最优超参数;④ 根据评估指标计算结果,调整模型参数;⑤ 对预测结果进行反归一化,得到预测结果的真实值。
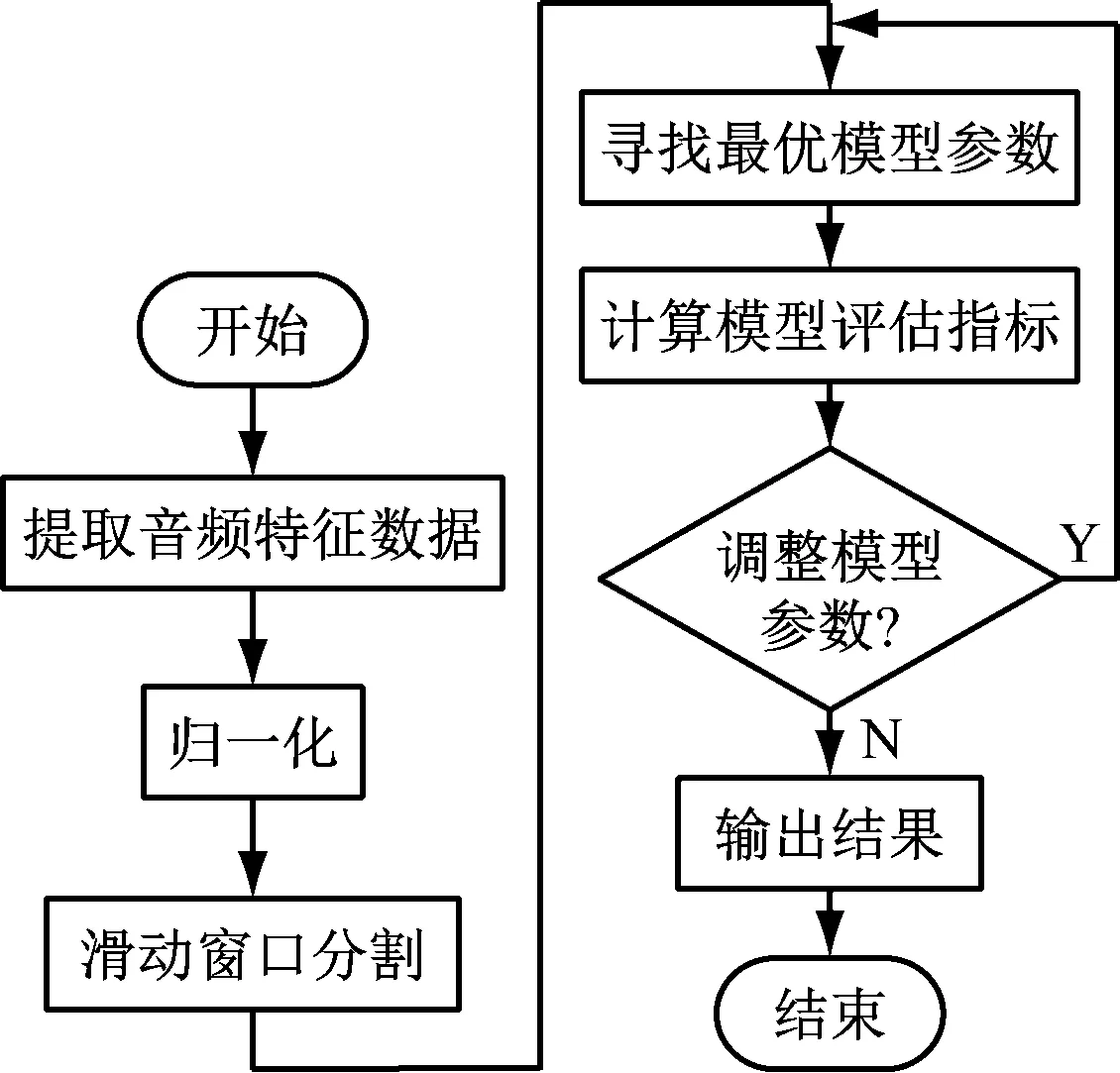
图6 Res-CNN-LSTM模型训练流程Fig.6 Res-CNN-LSTM model training process
4.2 模型参数
经过多次实验调试,设置预测模型的第1个CNN卷积层的卷积核大小为64,步长为16,数量为8,采用“same”作为数据边界填充方式;第2个卷积层卷积核大小为3,数据边界填充方式为“same”;最后一层卷积的卷积核大小为1,以减小数据维度,降低模型计算量。在LSTM网络中采用“Dropout”,使模型在训练过程中以一定概率将神经元置零,解决模型过拟合问题;采用随时间反向传播(Back-Propagation Through Time,BPTT)算法[16]不断更新模型的权重矩阵;残差块个数为8;将批大小和迭代次数作为变量,根据目标函数的最优解,使用网格搜索法得到模型的批大小为128,迭代次数为500。
4.3 模型评估指标
选取平均绝对误差(Mean Absolute Error,MAE)和均方根误差(Root Mean Square Error,RMSE)作为模型性能评估指标[17]。MAE用来判断预测值与真实值的误差,也可判断预测值与真实值之间的拟合度,其值越小,说明预测值越接近真实值;RMSE用来评判预测值与真实值之间的偏差,其值越小,说明模型性能越好。
4.4 实验结果
4.4.1 滤波降噪结果
采用高通滤波器和Boll谱减法对原始音频信号进行滤波降噪的效果如图7所示。可看出原始音频信号中包含大量噪声信号,对其进行滤波降噪后可消除大部分噪声信号,且很好地保留了有用信号。
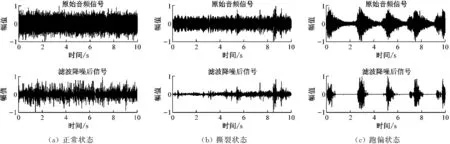
图7 滤波降噪前后音频信号波形Fig.7 Waveforms of audio signal before and after filtering and noise reduction
4.4.2 音频特征提取结果
分别提取带式输送机3种运行状态下音频信号MFCC0特征,如图8所示。当带式输送机正常运行时,音频信号变化平稳,且主要集中在低频,得到的MFCC0特征变化平缓,幅值较小。当带式输送机发生撕裂故障时,产生故障冲击,音频信号中含有大量高频信号,提取的MFCC0特征幅值呈明显上升趋势。当带式输送机发生跑偏故障时,由于输送带上的煤炭分布不均衡,音频信号中的高频分量具有一定的周期性,MFCC0特征幅值也呈周期性变化,且幅值变化区间较大。因此,通过音频信号的MFCC0特征可很好地区分不同运行状态,反映不同运行状态的趋势。
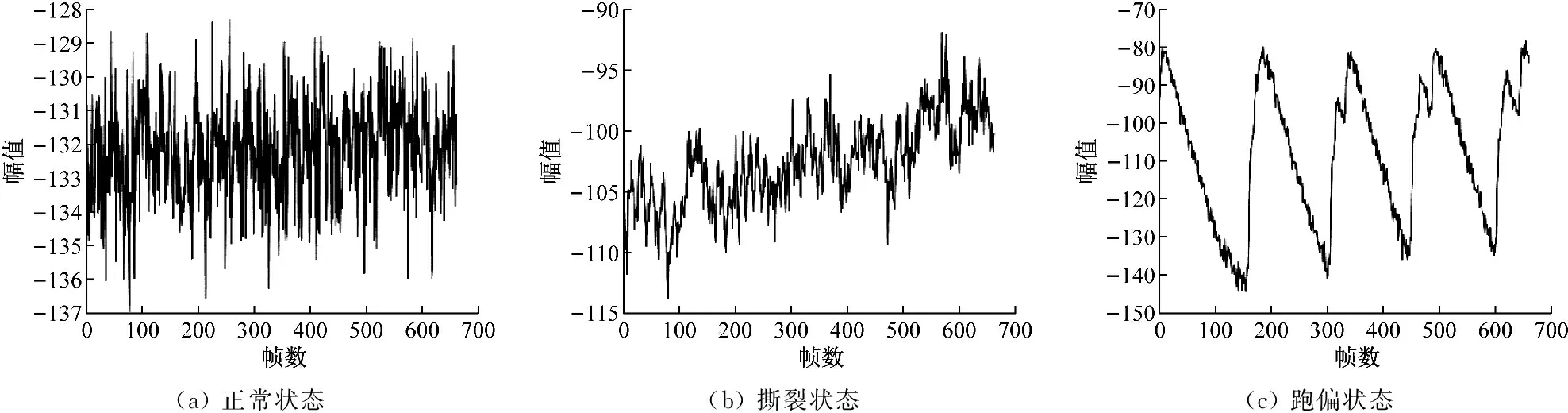
图8 带式输送机不同运行状态下音频信号MFCC0特征Fig.8 Characteristics of audio signal MFCC0 under different operation states of belt conveyor
4.4.3 运行状态预测结果
为验证本文提出的Res-CNN-LSTM预测模型的准确性,将其与CNN,LSTM,CNN-LSTM模型进行对比。不同模型训练时的损失函数曲线如图9所示。可看出随着迭代次数增加,4种模型的损失函数值均趋于收敛;CNN和LSTM模型的收敛效果较差,损失函数值变化较大;随着迭代次数增加,CNN-LSTM模型损失函数值出现明显波动;相较于其他模型,Res-CNN-LSTM模型损失函数收敛速度更快,且损失函数值变化更稳定。
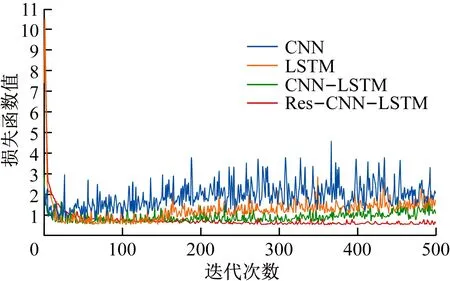
图9 不同预测模型损失函数曲线Fig.9 Loss function curves of different prediction models
将带式输送机3种运行状态下的音频特征输入不同预测模型,得到带式输送机运行状态预测结果,如图10所示。
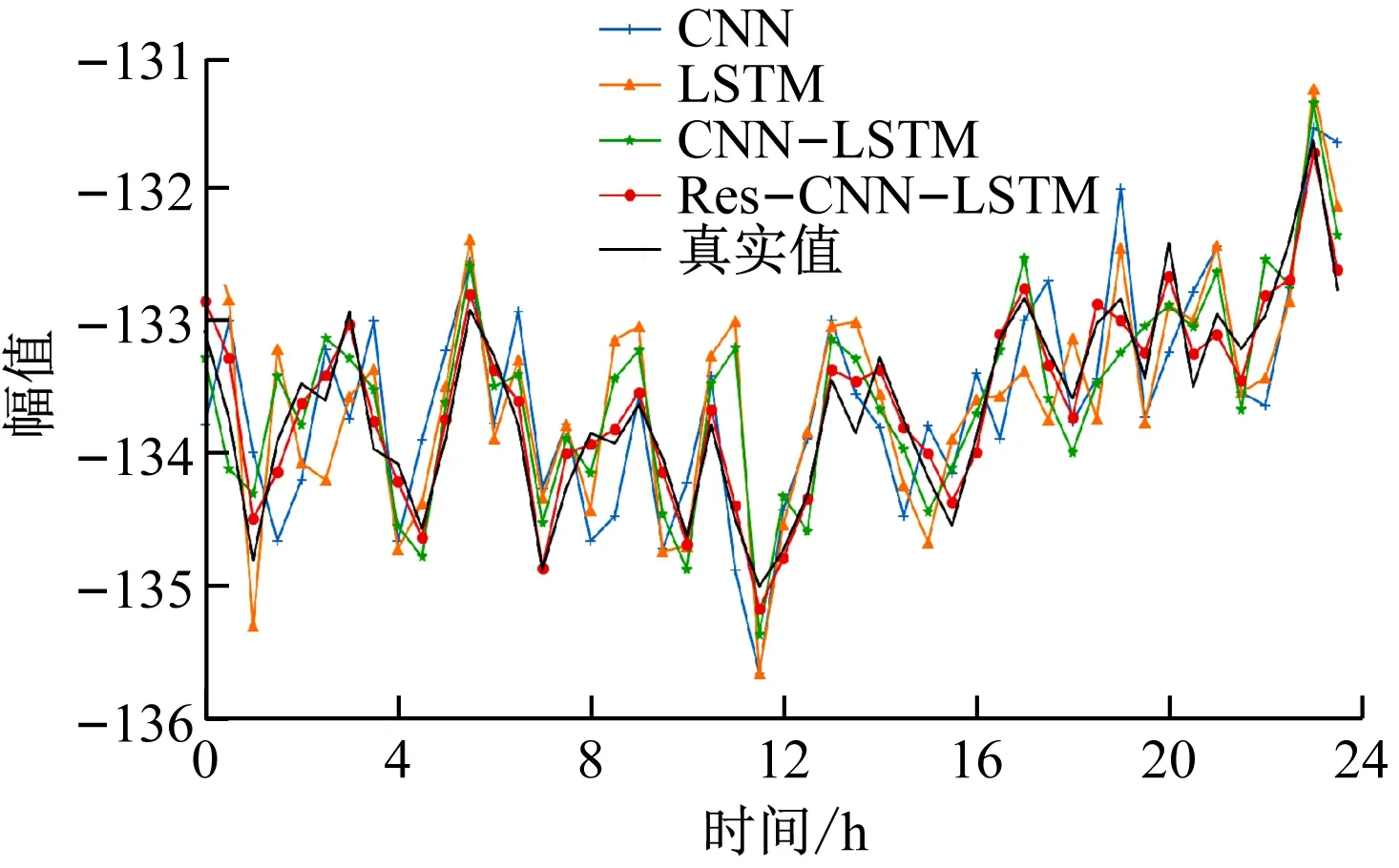
(a) 正常状态
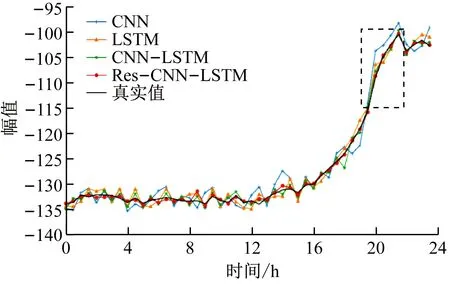
(b) 撕裂状态
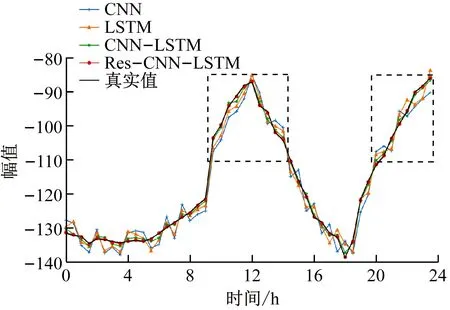
(c) 跑偏状态
从图10可看出4种模型均可有效拟合带式输送机运行状态变化趋势;CNN和LSTM模型的预测值相比于真实值偏差较大;CNN-LSTM模型的预测结果优于CNN和LSTM模型,但对正常和撕裂运行状态的预测结果偏差大于Res-CNN-LSTM模型;Res-CNN-LSTM模型对3种运行状态的预测结果优于其他模型,与真实值偏差较小,且该模型可对故障运行状态的故障变化趋势(虚线框处)进行准确预测。
不同预测模型性能评估结果见表1。可看出Res-CNN-LSTM模型的MAE和RMSE均低于其他模型,表明该模型对带式输送机运行状态的预测更准确。
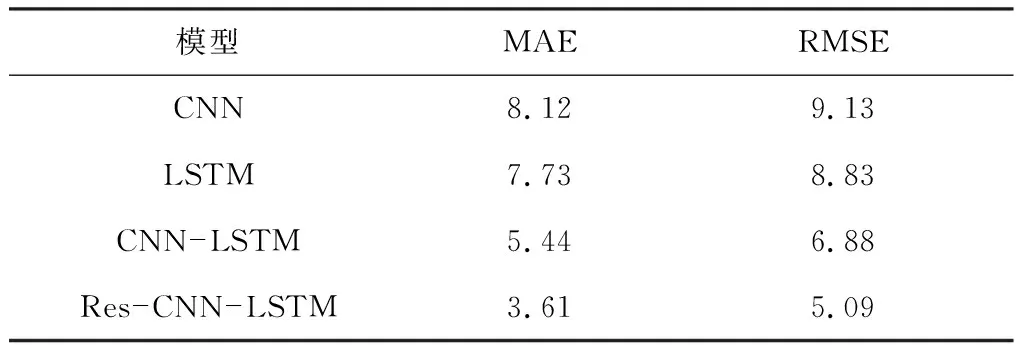
表1 不同预测模型性能评估结果Table 1 Performance evaluation results of different prediction models
5 结语
提出了一种基于音频信号特征和Res-CNN-LSTM模型的带式输送机运行状态预测方法。通过提取带式输送机不同运行状态时的音频信号MFCC0特征,可以少量数据获得更多的带式输送机运行状态信息,减少预测模型的输入数据量;Res-CNN-LSTM模型利用CNN和LSTM网络分别提取MFCC0的空间特征信息与时间特征信息,并且在CNN中添加残差块,以提取更多的特征信息,同时避免了过拟合与性能衰退问题。实验结果表明,通过音频信号的MFCC0特征可准确反映带式输送机不同运行状态;与CNN,LSTM,CNN-LSTM模型相比,Res-CNN-LSTM模型对带式输送机运行状态的预测更准确。

