基于有向网络非对等关系的异常子图识别算法

石灏苒, 吉立新, 刘树新, 张奕鸣

中国人民解放军战略支援部队信息工程大学 郑州 中国 450001

1 引言

异常检测作为数据挖掘领域中的经典问题, 主要解决如何发现数据集合中不符合预期的对象, 模式或现象[1]。根据所利用特征, 可分为基于结构特征, 流量特征[2], 用户属性特征[3-4], 文本内容特征[5]等异常检测方法。其中基于结构特征的图异常检测方法, 由于具有特征易获得、不易伪造且异常可解释性较强的特点[6], 在近年来备受关注并在电信诈骗检测[7], 网络入侵检测[8], 社交网络虚假用户识别[9-10]等多个领域均有普遍应用。

根据对异常结构定义不同, 可将图异常检测分为基于结构, 基于概率, 基于社团及基于压缩分解4种方法[11]。基于结构方法通过节点间共同结构或连通路径衡量节点相似性, 将不相似节点间连边所组成的结构定义为异常结构[12-14]。基于概率方法根据节点正常结构特征构建概率分布模型, 将异常结构定义为偏离分布的离群点[15], 如提取一阶自我中心网络(egonet)结构特征的Oddball方法[16]。基于社团方法通过划分社团识别密集异常结构或跨社团异常行为[17-18], 如文献[8]通过划分社团发现跨社团的网络入侵行为, 该方法具有较好异常可解释性, 但由于对网络特征依赖较强, 使用场景较为局限。基于压缩分解方法将异常结构定义为结构噪声, 通过总结网络生成规律发现不符合规律的异常子结构, 如设置残差矩阵非负约束的NrMF算法[19], 利用低秩矩阵自表示的LFNR算法[20]等, 该方法对异常连边这类单点异常具有较好识别精度, 但对异常子图这类集体异常识别效果不够理想, 且较依赖于网络规律性。相比基于社团和基于压缩分解方法, 基于概率和结构的方法从节点邻域与路径出发提取特征, 具有较高普适性及识别精度鲁棒性, 近年来在图异常检测领域受到较多关注[11]。

现存的基于结构和概率方法已对无向结构特征有较为深入研究, 但对于有向网络中节点间非对等关系特征在异常结构挖掘中的作用仍待进一步发掘。因此, 本文从有向网络结构出发, 利用三阶模体作为连边距离度量, 从节点egonet结构量化分析节点与邻居间非对等关系强度, 并以图密度形式表示, 后结合基于密度的影响异常因子算法(Influenced outlierness, INFLO)识别异常子图。与大多目前将网络结构映射为多维特征空间中孤立点的方法相比, 本文方法进一步考虑了节点的实际物理联系, 以及节点间关系不对称的实际情况。通过在具有4种不同异常类型的合成网络结构与存在真实异常的网络结构上分别进行了试验, 验证了该方法在不同网络结构下对不同的异常类型均具有较高检测精度与鲁棒性。

2 相关工作

由于异常检测所面临的问题往往是从无标签数据中发现不符合预期的数据, 这类数据占比极小使得有监督方法难以此进行学习建立具有较好检测效果的模型, 且基于历史数据特征学习所得模型对于未知异常不能起到较好检测效果。因此无监督学习技术目前仍是异常检测主流技术, 其主要可以分为基于近邻, 基于统计分析, 基于聚类, 基于子空间四类方法[21]。其中基于近邻方法由于计算复杂度低, 普适性与可解释性较强, 受到了长期关注且已有众多经典方法, 如K-近邻(K-NearesNeighbor, KNN), 局部异常因子(Local outlier factor, LOF)等, 并在图异常检测领域被广泛用于对结构特征进行分析, 以下对其研究现状进行主要介绍。

2.1 基于局部近邻异常检测方法

基于近邻的局部方法也被称作基于密度的方法。KNN这类从全局出发的方法, 虽能找到明显远离大多数数据的异常点, 但对于离聚类较近的异常点却无法起到较好检测效果。由此, LOF算法最先引入了局部异常概念[22], 对于特征空间中某一数据点p, 首先计算与其最近的k个节点欧氏距离,k个节点中距其最远节点o的距离k-distance(o)也被称为k-最远可达距离。

根据对距节点p最近的k个节点距离计算, 可以得到这k个节点距点p的平均距离, 以此根据距离倒数可以得到该节点局部密度。

同理计算节点p的k个最近节点的局部密度, 节点p局部密度与这k个节点局部密度的比值平均值即为该节点的异常分数。

LOF算法虽可对局部异常进行较为精准的量化分析, 但却容易将边界处的点误判为异常。因此INFLO算法在LOF基础上, 考虑了k近邻点和反向近邻集合[23], 即在计算数据点p局部密度时, 令节点p最近的k个节点邻居集为N(k), 当节点p作为其他节点的k近邻时, 将这些节点也加入p的邻居集中, 记为RN(k), 节点p最终邻居节点集为SN(k)=N(k)+RN(k), 局部密度计算如下。

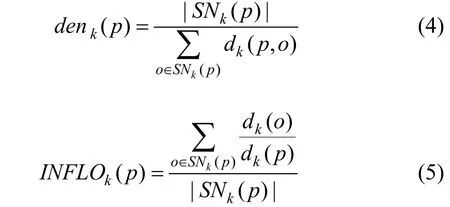
Akoglu L等人[16]最早从图特征角度, 提取节点一阶无向egonet结构特征构建特征空间, 在拟合函数基础上利用LOF方法统计分析, 以此发现偏离拟合函数且与其k近邻较远的离群点, 实现了对过于稀疏或密集的异常子图识别。文献[24]在这一结构特征基础上运用层次聚类对离群点检测方法进行了改进。文献[25]进一步考虑了节点的二阶无向egonet结构特征, 通过提取节点本身与周围节点一阶egonet闭合三元组比值以及节点与连边等特征构建特征空间, 即在节点无向二阶邻域特征基础上, 运用INFLO方法进行统计分析, 进一步提高了检测精度。

2.2 有向网络模体结构特征

相比无向结构, 有向网络通过连边方向进一步明确了行为主客体, 相关联个体间由于主客体不同可能处于非对等关系之中, 文献[26-27]根据连边方向将异常子图定义为“火山”(volcano)与“黑洞”(blackhole)这类行为过于发散或汇聚的模式, 并运用剪枝方法挖掘这种关系异常不对等的结构。在连边方向特征基础上, 模体作为有向网络特有结构, 其定义为在目标网络中出现次数远超过在随机网络中出现次数的频繁且独特的子图模式[28], 对连边方向特征进行了整合, 体现了个体间直接与间接非对等关系, 可更好突出这类异常模式特征。高阶模体由于计算复杂度高且难以表示, 目前研究中主要还是从三阶模体提取有向网络结构特征, 不同于无向三元组只存在闭合和非闭合两种结构, 三阶模体根据是否存在互惠边以及连边方向不同, 可以分为13种同形异构体, 如表1所示。

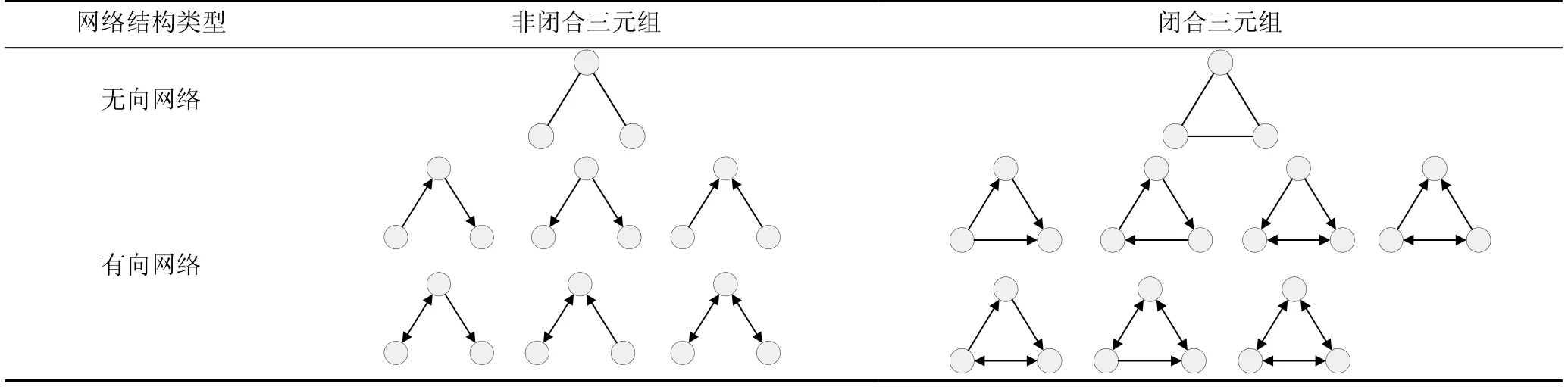
表1 不同类型网络中三元组结构 Table 1 Triple structure in different types of networks

非闭合有向三元组结构在链路预测研究中常被作为预测器以还原缺失连边, 即一条连边的加入若能使更多预测器结构转变为目标模体结构, 则其出现的概率就越大[29-30]。张鹏等人[12]认为当这种根据结构相似性衡量节点间相似程度的方法运用在已产生连边的节点对间时, 其结构相似性可看作对连边的距离度量, 用以表示连边真实性或节点双方紧密程度。Kagan等人[31]基于这一思想, 在对连边真实性及紧密程度度量的基础上, 进一步聚焦于产生行为的个体, 通过连边真实性反映节点异常程度, 以此挖掘异常节点。Zhang等人[32]进一步考虑了行为方向信息, 根据3-FFL有向模体提出的DCN(Directed Common Neighbors), DAA(Directed Adamic Adar)等指标在预测缺失连边与识别异常连边均具有较好的效果, 证明了其在描述连边生成机制以及作为结构特征的有效性, 并可较好表示节点间结构相似性以及关系不对等性, 其结构如图1所示。

图1 3-FFL结构示意图 Fig. 1 Schematic diagram of 3-FFL structure

3 局部有向异常因子

节点间有向路径代表信息传递方向, 有向路径数量以及方向共同决定了节点间紧密程度。以电信网通信为例, 用户向另一用户单向通信, 仅代表该用户存在想要建立关系的目的, 但不代表目标用户与通信行为发出者具有紧密联系。即仅当用户双方具有频繁对称通信行为, 才能代表用户双方存在紧密关系, 反之, 若某节点频繁向多个不相关目标用户进行通信且均未被回应, 则可能是一异常用户, 如电信诈骗者等, 该类异常特征也常见于网络扫描、金融诈骗等异常场景。目前基于节点邻域结构特征的图异常检测方法主要是提取单个节点无向邻域特征构建特征空间, 根据节点邻域结构映射到特征空间中的数据点间距离关系发现异常结构。然而, 对于网络结构数据中的异常, 数据对象被视为独立存在于多维空间中的点, 其相互依赖特征也在映射过程中被忽略, 且难以确定最佳的最近邻k值, 将导致异常检测精度的不稳定性。因此本文将从实际连接关系出发, 首先根据三阶模体特征作为连边距离度量, 根据节点最近邻度量以该节点为中心的子图异常分数, 并提出异常子图识别算法。

3.1 节点非对等联系强度分析量化

传统图异常检测方法研究中, 将个体间交互关系抽象为复杂网络结构, 节点代表个体, 连边代表行为。由于异常行为由异常用户直接发出, 因此节点的一阶结构信息包含了最主要的异常行为特征。取节点与其邻居作为节点集, 并取节点与邻居及其邻居间通联关系作为连边集, 所共同构成的网络结构被称为节点自我中心网络(egonet)。如图2给出了该结构示意图, 其由若干三元组所构成。

图2 不同类型网络egonet结构示意图 Fig. 2 Schematic diagram of egonet structure of different types of networks

在无向网络中, 三阶连通子图只具有封闭与非 封闭三元组两种结构, 节点与邻居节点间连边距离由共同邻居数量决定, 即节点双方拥有共同结构越多, 节点间距离越近, 但使用无向共同邻居结构作为距离度量过于粗粒化, 对于结构完全一致的两对节点无法进一步进行区分。而在考虑有向信息后, 3-FFL结构可根据节点间一阶及二阶有效连通路径更准确描述节点间距离。相比图2(a), 图2(b)的有向网络进一步刻画了信息传递的方向, 如在节点对(p,b)间, 节点p存在通向节点b的一阶路径p→b, 节点b存在通向节点p的二阶连通路径b→a→p; 而在节点对(p,e)间, 节点p存在通向节点e的一阶路径p→e与二阶路径p→f→e, 但节点e不存在相应反馈通信路径。因此两相对比, 在无向网络中结构完全相同的节点对(p,b)与(p,e), 在考虑了结构方向信息后可发现其节点对间距离具有明显差异, 可见行为方向可对节点间疏离程度进一步进行细粒度区分。

在基于局部近邻异常检测方法中, 如INFLO方法, 首先根据设定的k值找到距离数据点p最近的k个节点, 作为邻居节点集N(p), 后若点p亦属于其他数据点的k近邻, 则也将该节点加入邻居节点集, 形成反向邻居节点集RN(p)。由此得到最终邻居节点集SN(p)=N(p)+RN(p), 以此计算SN(p)距点p的平均距离倒数得到该节点局部密度, 再根据节点与邻居节点密度对比达到发现离群点目的。由于节点间连边可根据节点结构相似性转化为对节点间距离的度量, 基于这一思想, 节点一阶有向子图结构可以分解为由出连边组成的出子图与由入连边组成的入子图, 如图3所示, 假设k值即为节点p的出子图邻居数量, 其邻居节点集为N(p)={a,b,d,e}, 而入子图代表节点p属于其邻居节点的k近邻, 则入子图的邻居节点集为RN(p)={c,d}, 节点p的k近邻和反向k近邻最终组成了节点p的egonet结构邻居节点集SN(p)= {a,b,c,d,e}。

图3 有向子图结构类比INFLO方法示意图 Fig. 3 Schematic diagram of directed subgraph structure analogy INFLO

显然, 相比在特征空间基础上进行离群点检测, 本文方法局部近邻k值由节点邻域结构直接确定, 避免了k值确定不合适导致的局部异常衡量不准确情况。且在有向网络中由于路径方向不同所导致的节点间关系强度非对等可由有向连边的距离度量体现, 如图3中节点p相对节点d距离为1/4, 而节点d相对节点p距离为1/2, 该距离可根据3-FFL模体结构可进行量化, 以下对其具体定义进行介绍。

定义1. 基于模体结构的节点间距离度量定义网络结构G=(V,E), 对于某一节点x∈V, 抽取其自我中心网络ego_x={(Vx,Ex)|Vx=Γ(x),Ex}, 如图4所示。

图4 节点一阶有向子图交互示意图 Fig. 4 Interaction of first-order directed subgraphs

根据以上模体分析可知, 3-FFL结构可看作一条一阶有向路径与二阶有向路径的组合, 因此对于组成该结构的任意节点对, 该结构可从一阶与二阶角度对其节点间相对距离进行衡量, 进而描述其关系非对等程度。而3-FFL预测器结构作为3-FFL缺失一条连边所构成的非闭合三元组结构, 虽不存在直接路径, 但同样可从节点间二阶路径角度对进行描述。如图4中节点(x,y,z1)所构成的3-FFL结构可从一阶与二阶路径上对节点y到x的节点距离进行度量, 而从节点x到y虽不存在直接一阶有向路径, 但节点(x,y,z2)所构成的3-FFL预测器仍可从二阶路径角度对节点x到y的距离进行度量。由此可根据以上对x到y以及y到x的距离进行对比得到节点对(x,y)间通信关系的非对等程度。

因此当节点对(x,y)间至少存在一条连边lxy, 且该连边所构成的闭合三元组3-FFL结构或非闭合三元组3-FFL预测器结构越多, 则可认为该连边对节点间紧密联系贡献越大, 连边的距离度量值越小, 这种根据连边对节点间连通性贡献进行的距离度量可表示为下式。其中Sxy代表节点x与y所共同构成的3-FFL模体数量及非闭合的3-FFL模体结构预测器数量, 其意义是衡量节点间二阶路径对节点对间疏离程度影响。而|lxy| 则代表节点间直接存在的连边数量对节点对紧密程度的贡献, 显然, 存在互惠边的节点对比仅存在单向连边的节点对, 其节点连接更加紧密, 联系也更加对称。在节点egonet结构中, 该度量对中心节点及其邻居间紧密程度进行衡量, 以此获得中心节点间距离各邻居节点疏离程度的整体视野, 进而对其密度进行量化。

egonet结构中除节点间局部联系外, 还可能存在可以进行信息传输的较长有效路径, 如图5所示。路径长度由构成的有向连边距离决定, 即所构成路径的连边距离度量值越小, 路径信息传输能力越强, 对于节点对间连通性贡献越大。因此在获得每条连边距离度量后, 根据下式可以计算路径对节点对间的距离贡献, 根据具体情况可对考虑的路径最大长度进行调整。

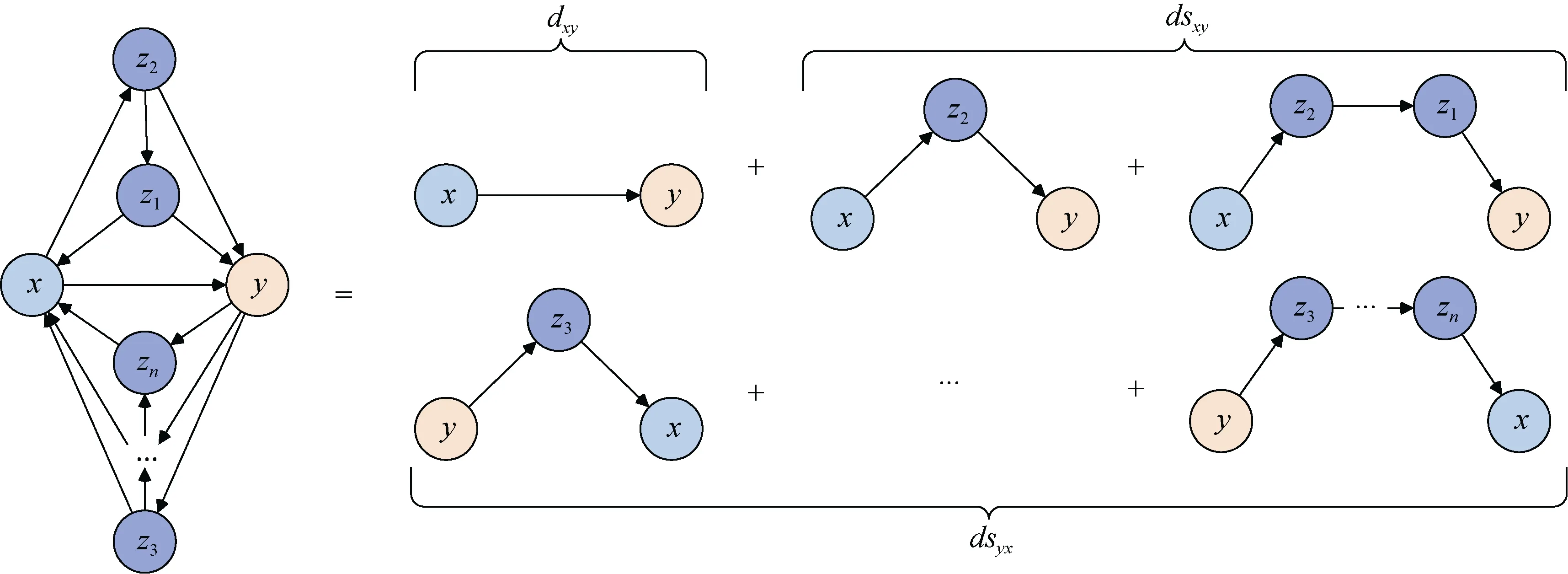
图5 节点一阶子图间连通路径分析示意图 Fig. 5 Connectivity path analysis between first-order subgraphs

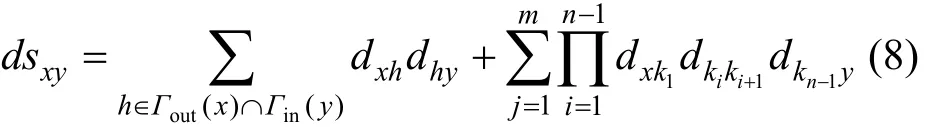
在对节点间所有连通路径的距离进行度量后, 可以由此得到节点间的平均距离, 如下式, 其中 |Lxy| 为节点x向y方向的所有有效路径。显然, 当节点间直接联系越近或是组成连通路径上的节点, 即x与y的邻居节点间距离越紧密, 都可使最终x相对y的平均距离较小。由此根据从x到y以及从y到x的相对距离差值, 可以得到节点对(x,y)间联系的非对等强度度量, 由xyt↔表示。该值绝对值表示联系非对等强度, 当该值为负时, 表示邻居节点相对目标节点的距离更近, 联系更加紧密, 而目标节点相对邻居节点距离更远, 联系更加疏远, 反之同理。

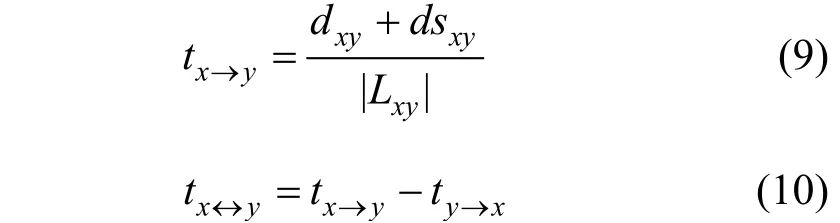
3.2 局部有向异常因子

在egonet结构中, 根据节点与其所有邻居节点非对等联系的度量之和, 可以从整体角度对该节点相对局部结构的离群值进行量化, 其计算如下。该值受邻居节点数量以及节点与各邻居节点非对等联系差异的共同影响。即当个体邻居节点明显较多, 节点与邻居节点及邻居节点间行为非对等强度较大, 则以该节点为中心的子图结构离群值越大。

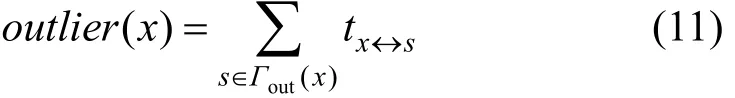
但由于复杂网络结构的同质性与自组织特性[33], 处于网络不同位置的结构可能相对整体网络结构更加密集或稀疏, 这将导致处于密集社团中的正常节点具有较高离群值, 而处于边缘结构中的异常节点却离群值较小。为解决这一问题, 基于社团内节点行为呈现趋同性这一特点, 在根据egonet结构对节点子图离群值进行度量后, 还需进一步与其邻居节点子图离群值进行对比, 以避免处于网络结构密集区域的正常结构被错误识别为异常子图。

定义2. 局部有向异常因子为直观度量节点与其邻居节点的离群值差异, 将其转化为节点子图密度进行表示, 如下式。当节点与各邻居节点联系都较对称时, 则认为其与各邻居节点连接都较紧密, egonet结构密度越大; 而当其与各邻居节点联系呈现向同一方向不对称联系的情况, 则认为各邻居与其联系较为疏远, egonet结构密度越小。其绝对值为对这种紧密程度的度量, 符号表示联系不对称的方向, 即为负时, egonet结构中连边方向总体呈现向目标节点汇聚的现象, 为正时呈现由目标节点向外发散的现象。

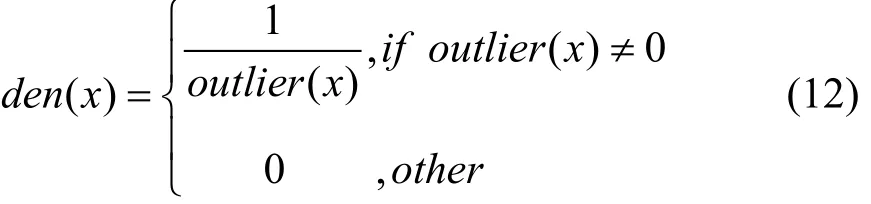
由于复杂网络结构的自组织特性, 对于正常节点而言, 有较大概率与其邻居节点处于同一社团, 且出于正常目的, 其行为呈现趋同性与相似性, 在网络结构上表现为结构特征相近。而对于异常节点行为而言, 如电信诈骗, 网络攻击等, 作为入侵其他社团的恶意节点, 其行为目的明显与正常节点不一致, 即使经过伪装, 其网络结构特征与入侵社团内正常节点特征必定存在一定差异。根据这一推断, 为避免异常节点对其行为特征进行伪装, 使得仅从节点一阶egonet结构的稀疏与密集特征判断导致错误识别, 还需运用INFLO方法在对节点子图密度衡量基础上, 进一步对节点邻域特征与邻居节点邻域特征进行对比, 通过区域性信息进一步判断异常子图结构以提高识别准确率。

根据以上对于节点间非对等关系强度度量以及对于由这种节点关系所构成的子图密度度量。可以从节点间关系是否对等与子图间密度是否一致两个层面对节点子图异常程度进行衡量。前者主要关注于节点间关系特征, 后者则关注节点邻域在其所在局部区域的异常特征, 因此本文将两者结合共同对以节点为中心的异常egonet结构子图进行识别, 提出了局部有向异常因子(Local directed outlier factor, LDOF):

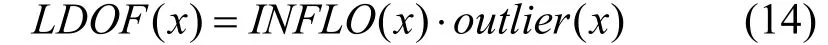
为更直观表述LDOF算法识别异常子图的具体步骤流程, 表2给出了LDOF算法的完整实现步骤。对于存在异常数据的网络结构, 将其记为G(V,E), 其 中V={v1,v2,…,vn}代表网络中所有节点的集合, E则为对应节点间通联关系所组成的连边集合。由于LDOF算法在衡量所得节点间距离受考虑的最大有效连通路径长度影响。因此需根据具体网络结构特性, 设计对应适合有效连通路径长度范围以达到最佳检测效果, 设该值为n。其决定了节点一阶egonet交互结构中, 衡量各连边权重时所利用的节点间最大有效连通路径长度。通过改变n可以对算法的计算复杂度与检测精度进行灵活调整, 并适用于不同类型网络结构。

表2 LDOF算法实现步骤 Table 2 Implementation steps of LDOF algorithm

4 实验分析

4.1 网络数据集介绍

本文选取了5个真实网络对所提方法有效性进行验证, 具体介绍如下:

(1) Politicalblogs(PB): 美国政治论坛的博客首页间通过超链接所构成网络, 节点表示网页, 连边表示网页之间的链接跳转关系。

(2) Email-EU-core(EU): 由大型欧洲研究机构的电子邮件数据生成网络, 节点对应于该机构中人员, 有向边表示某人已向另一人发送电子邮件。

(3) Wikivote(WV): 维基百科管理员选举投票所构成的网络, 节点代表维基百科用户, 连边表示用户间的投票关系。

(4) CTU-13_6(CTU): 存在网络扫描行为的计算机通信网络, 节点代表计算机网络上的设备, 连边代表节点间基于UDP, TCP, ICMP协议的流量记录。

(5) Relity-Call(RC): 存在骚扰电话的真实电信网通信数据, 节点代表通话设备, 连边代表用户间通信记录。

由于存在真实异常数据的网络难以获取且无法满足多角度定量分析的要求, 因此本文选取了EU, PB, WV 3个未标注异常的真实网络, 通过人为注入异常形成半仿真数据集对算法异常检测效率进行定量验证。之后在存在标注异常数据的网络CTU, RC中进行实际效果验证。以下是各网络的结构数据。

表3 网络数据集及其参数 Table 3 Network dataset with parameters

4.2 异常仿真类型

在实际存在异常的网络结构中, 异常用户在进行欺诈、入侵等异常行为时, 也会采取一些伪装措施避免被检测系统发现。文献[34]对异常行为在网络中的结构表现形式进行了分析, 提出了三类典型的网络异常结构。本文在此基础上, 分析设置了以下4类异常行为表现形式:

(1) 无伪装异常(Random): 异常节点随机向正常节点采取行为, 目标正常节点间相关性不强, 常见于电信诈骗, 垃圾邮件等场景。

(2) 偏向性伪装异常(Biased): 假设异常节点对于网络结构具有一定认识, 向某一正常节点采取行为的同时也对其邻居节点采取行为。通过这种向一个社团偏向性采取行为的方法达到伪装成正常节点, 或是针对某一特定群体采取对应行为以达到最优效果的目的。常见于计算机病毒传播控制, 谣言针对性传播等有较强目的性的异常场景。

(3) 劫持节点(Hijack): 异常用户通过控制网络中正常节点进而采取异常行为, 利用正常节点之前的正常历史通信行为对之后采取的异常行为进行掩饰。常见异常场景如DDos攻击之前的潜伏僵尸网络, 被控制主机在收到攻击指令前保持正常通信状态, 而在发起DDos攻击后转而采取有针对性的异常行为。

(4) 劫持-偏向性伪装节点(Bi-Hijack): 此类异常为以上两类异常结合, 异常用户在控制网络中正常节点后, 通过该节点向正常节点及其邻居节点采取行为, 具有正常历史通信行为作为掩饰的基础上, 在发起异常行为阶段也尽可能模仿正常节点通信行为特征, 以达到持续获取非法利益的目的, 常见于网络诈骗、金融诈骗等异常场景。

4.3 实验衡量指标及对比方法

4.3.1 检测精度衡量指标

为准确衡量异常子图识别算法检测精度, 本文选取了TPR, FPR, Precision, Accuracy 4种指标从对异常子图的查全率、误报率、查准率以及整体分类准确能力等方面来衡量算法异常检测能力, 具体介绍如下:

(1) 真正例率(True positive rate, TPR): 分类最终获得的正例集中, 真实情况为正例的比率, 用以衡量方法的正例分类质量, 也称作召回率。

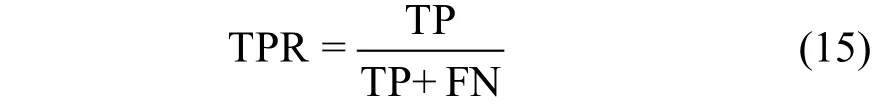
(2) 假正例率(False positive rate, FPR): 分类最终获得的正例集中真实情况为反例的数量, 占真实情况中反例的比率, 用以衡量方法对于负例的检测能力。

(3) 精确率(Precision): 计算所有真实情况为正例的样本中, 被正确分类为正例的比例, 主要关注正样本的分类准确率。

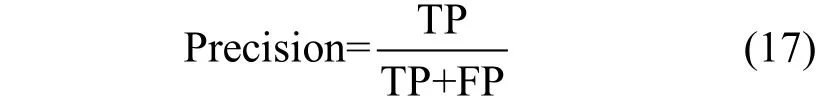
(4) 准确率(Accuracy): 从总体角度出发, 衡量所有被正确分类的正负例占总数的比率, 用以衡量方法整体分类能力。

其中, TP, FP, TN, FN分别代表被正确识别的正类, 被错误识别的正类, 被正确识别的负类, 被错误识别的负类。

4.3.2 对比方法

本文选取同样是基于图结构信息进行异常节点识别的Oddball方法[16], Fraudar方法[34]及ANMFG方法[35]作为本文所提算法的对比方法, 其中Oddball方法为定量异常检测方法, 其通过提取节点egonet无向结构特征, 将每个节点的egonet结构看作特征空间中一个样本点, 利用最小二乘法获取样本点在特征空间中分布的拟合函数, 最后结合LOF方法进行统计分析为每个样本点分配一个异常分数, 用以衡量节点egonet结构的异常程度。该方法不直接确定异常节点子图, 而是对各节点子图异常程度进行量化, 通过对量化值排序以确定可能的异常子图。

ANMFG方法同样作为一种定量异常检测方法, 在有向网络结构上利用非对称非负矩阵分解算法(asymmetric nonnegative matrix factorization, ANMF)[36], 将有向图聚类为节点的逻辑分组, 以此作为有向网络邻接矩阵分解的隐特征维度。且为提升检测精度与计算效率, 先基于非负二重奇异值分解方法(Nonnegative Double Singular Value Decom- position, NNSVD)进行初始化, 后利用ANMF进行非对称矩阵分解直到收敛。分别得到各节点在出连边与入连边方向特征上相对图节点的离群程度, 整合以上离群值并结合节点之间直接与间接链接度量最终对某一节点相对网络的离群程度进行衡量。

而Fraudar方法将异常检测看作分类问题, 基于节点间有向结构特征, 通过剪枝方法发现网络中存在的异常节点簇, 这些异常节点簇中节点一阶邻域结构异常特征表现为存在与该节点簇中其余节点的频繁通信行为, 而与该节点簇之外的节点间的连接却较为稀疏。该节点簇在网络中以异常密集子图的形式表示, 通过发现该类子图进而将其分类为异常, 相比定量分析方法, 定性分析方法对节点异常标签进行了明确分类, 但未对节点具体异常程度进行量化, 也存在无法突出异常子图间异常程度差异性的问题。

本文方法基于一阶有向邻域信息对各节点子图进行异常量化分析, 属于定量分析方法。所以首先利用同是定量分析的基于一阶无向邻域结构信息的Oddball方法与本文方法进行比较, 以证明个体间行为非对等特性对于异常检测精度提升的有效性, 以及对异常区分能力的改善。后为突出本文方法在使用同样异常行为特征条件下, 相比其他方法的在异常检测精度上的提升, 使用了同样利用了行为方向特征的定量分析方法ANMFG及定性分析方法Fraudar进行比较。与前者对比以突出同样维度信息条件下本文方法的异常量化能力, 而与后者对比以突出同样维度信息条件下本文方法与定性的异常检测方法的检测精度区别。

4.4 实验仿真结果

由于在实际情况中, 存在真实异常数据难以获得, 异常类型单一, 异常样本数量稀少等问题可能导致无法全面衡量各类方法实际异常检测能力, 且所标注数据集由于数据处理过程中操作不当仍可能存在错误标注, 影响实验结果。因此为从各方面衡量各方法异常检测能力, 参照目前图异常检测研究中主流仿真异常数据生成方法[6], 在PB, EU, WV 3个真实但未进行异常标注的网络中按以上分析的4种异常类型分4种情况构造半仿真数据集。每种情况下人为依次注入100个异常节点构成对应的半仿真网络数据集, 其中每个节点在注入网络时按照对应异常类型与网络中其他节点产生连接, 由此生成的半仿真网络中可能存在单个异常节点构成的异常子图或是多个异常节点相互连接构成的异常节点簇子图。其中注入的异常节点产生的连边数量与其所注入网络的平均度一致。将Oddball与Fraudar两种方法异常检测效果与本文方法进行比较, 并使用TPR, FPR, Precision三种指标进行衡量, 其中计算Precision时L设置为100, 本文方法考虑的路径最大长度n设为2, 效果如表4所示, 实验结果由10次重复实验值平均所得。

表4 各方法对4种异常情况检测精度 Table 4 Detection accuracy of each method for four abnormal situations

根据以上实验结果分析可得出以下结论, 当异常子图规模趋近于网络平均子图规模时, 在注入Random与Hijack异常类型的网络中, 各方法均能达到一定识别精度。相对Random异常, Hijack对各方法检测精度存在不同程度影响, 其中对ANMFG方法影响最明显。主要原因是由于ANMFG根据节点出入连边与周围节点的直接与间接关系计算相对网络整体离群值, 而Hijack异常节点由于是劫持正常节点后进一步采取异常行为生成, 因此其本身与一部分邻居节点的直接与间接连接就较为紧密, 降低了其相对网络结构的离群程度。而对于Oddball, 虽然其也基于节点局部结构紧密程度衡量节点子图异常程度, 但主要是与同等规模节点子图进行对比, Hijack虽改变其局部结构但随着节点采取新的异常行为, 使其与同规模结构产生了一定差异, 因此对其影响有限, 但利用局部信息也使其对Random与Hijack异常无法达到较高异常识别精度。本文所提出的LDOF方法则综合考虑了以上问题, 从有向局部结构出发与同规模结构进行对比同时, 还对节点子图密度进行衡量, 与区域内周围子图密度进行对比, 针对Random与Hijack异常类型均有较高识别精度。

而在注入Biased与Bi-Hijack异常类型的网络中, 由于这两类异常类型节点是对目标节点采取异常行为后, 搜索该目标邻居节点继续行为从而生成对应 异常子图。与Random与Hijack异常类型相比, 节点子图中邻居节点间连接更加紧密, 其局部结构异常特征被较好隐藏, 因此对于ANMFG方法而言, 其检测精度随网络结构特性不同发生较大波动, Oddball检测能力由于网络结构不同也在这种扰动下检测精度趋于不稳定。而LDOF算法由于考虑了节点子图密度相比邻居节点子图密度的离群程度, 当节点子图中邻居节点连接紧密时, 仍能通过异常节点与周围邻居节点间的非对等关系突出其行为的异常特征, 保证一定的异常识别精度并具有较好的鲁棒性。

而对于Fraudar而言, 虽然在四种异常类型上均具有较为稳定的识别精度, 但可见由于其作为异常分类方法, 直接分类节点是否异常使其相比其他方法的误报率FPR明显较大, 且异常检测能力根据网络结构特点不同波动较大。

以上从精确度, 查准率与误报率三个方面对各方法异常检测的精确能力进行了刻画, 但仅在异常子图规模与所注入网络平均度相同条件下, 从前100个节点的识别表现衡量各方法的异常检测能力仍不全面, 还需进一步在其他条件下对各方法进行比较。因此为衡量4种方法的整体异常检测能力, 使用Accuracy从查准及误报两方面衡量各方法的全局分类能力, 如图6所示。

图6 各方法在4种异常类型情况下不同网络中Accuracy度量 Fig. 6 Accuracy of each method in different networks under four abnormal types

可见, 当在PB, EU, WV 3个未标注异常的网络结构中, 根据各网络平均度按4种异常类型分别注入100个异常节点后用本文方法与各对比方法进行异常检测。从全局分类效果来看, 本文方法相比对比方法也仍具有更为稳定且有效的检测效果。Fraudar作为分类方法, 当网络中各节点簇间连接关系普遍不紧密时, 其可对异常子图达到较高准确度, 但当网络结构较密集, 异常节点子图特征不突出时, 其分类范围将明显扩大导致Accuracy值降低。

以上对各方法从异常识别精确能力与整体分类能力两方面进行比较都是基于异常子图规模固定假设条件下进行。为进一步验证各方法对不同规模的异常子图识别能力, 通过设置异常节点注入时与网络中各节点产生连接的概率以调整异常节点连接节点数占网络总节点数的比例, 并在区间[0.02,0.12]内对4种异常类型进行验证, 采用Precision进行衡量, 其中L值设为100, 效果如图7所示。观察实验结果可发现, 4种方法对于Random与Hijack异常类型检测精度与异常子图规模总体呈现正相关趋势, 即异常子图规模越大, 异常特征越明显。

图7 各方法在不同网络4种异常情况下Precision度量 Fig. 7 Precision of each method in four abnormal cases of different networks

但对于有偏向性伪装的异常类型Biased与Bi-Hijack, Oddball与ANMFG方法检测精度明显降低, 且随着异常子图规模扩大, 检测精度并无明显提升。其原因可能为有偏向性异常由于选取互为邻居节点进行连接, 因此可以较好伪装为正常节点邻域结构, 在特征空间中与同规模正常结构相似。Oddball方法将目标节点egonet无向结构特征与网络中同样规模的egonet无向结构特征进行比较时, 有偏向伪装后的异常子图在不同规模下都能缩小与同规模子图结构的特征差异, 可较好躲避Oddball方法的检测; 同理, ANMFG方法虽进一步考虑了行为方向特征, 但仍是结合节点之间直接与间接链接设置隐特征, 当异常节点与目标社团连接较为紧密时, 分解过程中目标节点离群程度则难以突出。Fraudar方法虽然对于4种异常类型检测精度较为稳定, 但对于异常子图规模并不敏感, 且受网络结构规律性影响, 在不同网络中异常检测精度具有一定差别。

相比以上对比方法, LDOF方法在不同网络中对4种异常类型的检测精度均相对更加精确, 且对于有偏向性伪装异常的检测能力较为稳定, 并与其异常规模呈现正相关。在实际异常检测应用中可以较好的避免忽略大规模异常带来的损失。

由于以上对比方法中的Oddball方法, ANMFG方法与本文方法均为对节点异常程度进行排序的定量方法, 方法的准确度Precision取决于L的取值, 仅在L=100条件下对各方法异常检测能力精确性衡量仍不全面, 为进一步证明本文方法的异常检测能力与L取值的关系, 同样在PB, EU, WV 3个真实但未进行异常标注的网络中按以上分析的4种异常类型分4种情况构造半仿真数据集, 注入异常节点N=100, 注入异常节点产生的连边数量与其所注入网络的平均度一致。取50～500间不同L值计算其Precision, 并与Oddball方法与ANMFG方法进行比较, 结果如图8所示。

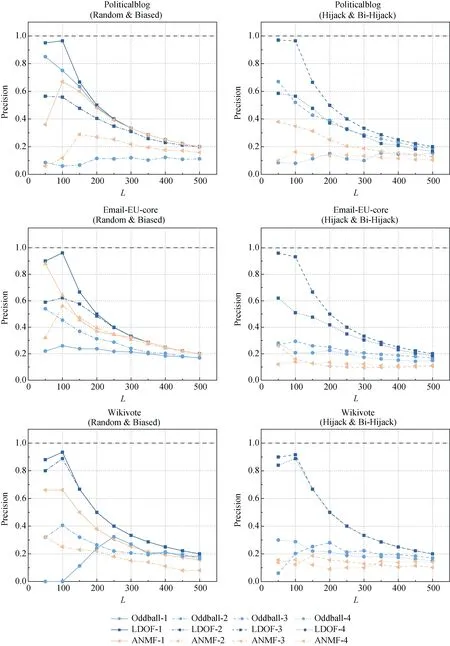
图8 各方法在不同L值下针对4种异常情况的Precision度量 Fig. 8 Precision of each method for four abnormal cases under different scales of L

4.5 真实数据集验证

以上通过在未标记异常的网络结构中人工注入异常节点, 生成存在不同异常类型, 不同规模异常子图结构的半仿真网络, 以此从异常检测的精确性与全局分类能力两方面对各方法进行比较评估。但在实际异常场景中, 网络中所存在的真实异常数据可能根据实际场景存在相应的隐蔽手段与独特的异常特征, 仿真实验并不能完全模拟还原这种异常行为。因此为验证本文所提的LDOF算法相比以上所选取的各异常检测算法, 在无监督条件下的真实异常场景中仍能达到更加精准的异常检测效果。选取了两个存在真实异常数据的复杂网络数据集: (1)CTU-13_6: CTU-13数据集是捷克理工大学于2011年捕获的僵尸网络流量数据集, 其包含在13种场景下僵尸网络在不同攻击阶段, 采取不同类型异常行为的流量数据集, 其多样性与真实性使其成为近年来异常检测领域内较为权威的数据集。该数据集中抓取的计算机网络实际流量数据由pcap文件格式存储, 包含网络扫描, 基于UDP, TCP, ICMP等协议的DDos攻击, 以及发起攻击前僵尸网络控制主机与受控节点间通信等真实异常行为数据。本文选取了存在水平网络扫描行为的场景6所对应的pcap文件, 根据节点间通信记录将其抽象为复杂网络形式进行分析。(2) Relity-Call(RC): 存在骚扰电话的真实电信网通信数据, 将通信设备间通信行为抽象为连边所构成的对应异常网络数据集, 其中, 节点代表通话设备, 连边代表用户间通信记录。

在CTU-13中的场景6异常数据集中, 记录了由12558个通信节点所组成的通信网络2.18h内的通信数据, 节点间通信数据基于IP, UDP, TCP, ICMP, HTTP协议进行传输。其中IP地址为“147.32.84.165”的主机为标记的异常主机, 其目的是水平扫描该网络中各节点IP地址, 为僵尸网络构建与选取DDos攻击目标做准备。为充分利用图特征实现对该数据集中存在的异常节点与行为精准检测, 数据处理过程中将通信节点间一次通信行为看作节点间产生的一条连边, 其中行为发出者为连边起点, 接收者为连边终点, 以此确定连边方向。若在一段时间内节点间存在同一方向的多次通信行为, 则通信行为产生的次数作为该有向连边的权值, 以此将该异常数据集抽象为存在异常节点与连边的有向加权网络结构。由于本文的LDOF方法与Oddball方法及ANMFG方法均为定量排序方法, 所以首先运用这三种方法对该数据集所有节点进行异常程度量化并排序, 结果如下: 异常主机在LDOF方法下排名为2; Oddball方法排名为17; ANMFG方法排名11; 而Fraudar方法是通过抽取行为异常的节点簇达到识别异常节点的目的, 本质是对节点进行分类, 根据该方法在该数据上最终分类获得的异常节点簇分析, 异常主机节点未被包含于异常分类结果中。

由于CTU-13虽然存在大量异常行为, 但过于集中, 异常节点个数较少。为避免单个异常节点特征的特殊性, 进一步使用Relity-Call异常数据集衡量各方法在同一数据集中对多个不同异常节点的识别能力。在Relity-Call异常数据集中, 记录了由6810个通信设备所组成的电信网的通话记录, 连边代表用户间的通话。该网络中存在90个异常通信设备, 因此将L值设为90, 并运用LDOF与Oddball方法及ANMFG方法对比进行异常检测, LDOF方法最终检出异常节点61个, 所得Precision值为67.78%; Oddball方法最终检出异常节点55个, 所得Precision值为61.11%; ANMFG方法最终检出异常节点43个, 所得Precision值为47.78%; Fraudar方法最终生成一个由151个节点组成的异常子图, 检出异常节点51个, 所得Precision值为33.77%。

通过以上真实数据集上实验, 显然, Fraudar方法虽然仍可检出大部分异常通信设备, 但抽取异常节点簇规模也相应较大, 准确率较低。而Oddball算法与ANMFG算法及本文LDOF方法异常检测效率较为接近, 由于在进行对比时, 将L值设为了90, 前90个节点都被认为是异常节点, 但在实际未知异常节点数量情况下, 该类方法仅可通过异常分数对节点异常程度进行判断。因此为进一步对比方法的异常检测能力, 在以上两个真实数据集上, 将各节点在两种方法下的异常分数归一化后进行比较, 如图9所示。

图9 真实数据集上各对比定量分析方法与LDOF算法异常量化比较 Fig. 9 Comparison of abnormal quantification between different control methods and LDOF algorithm on real datasets

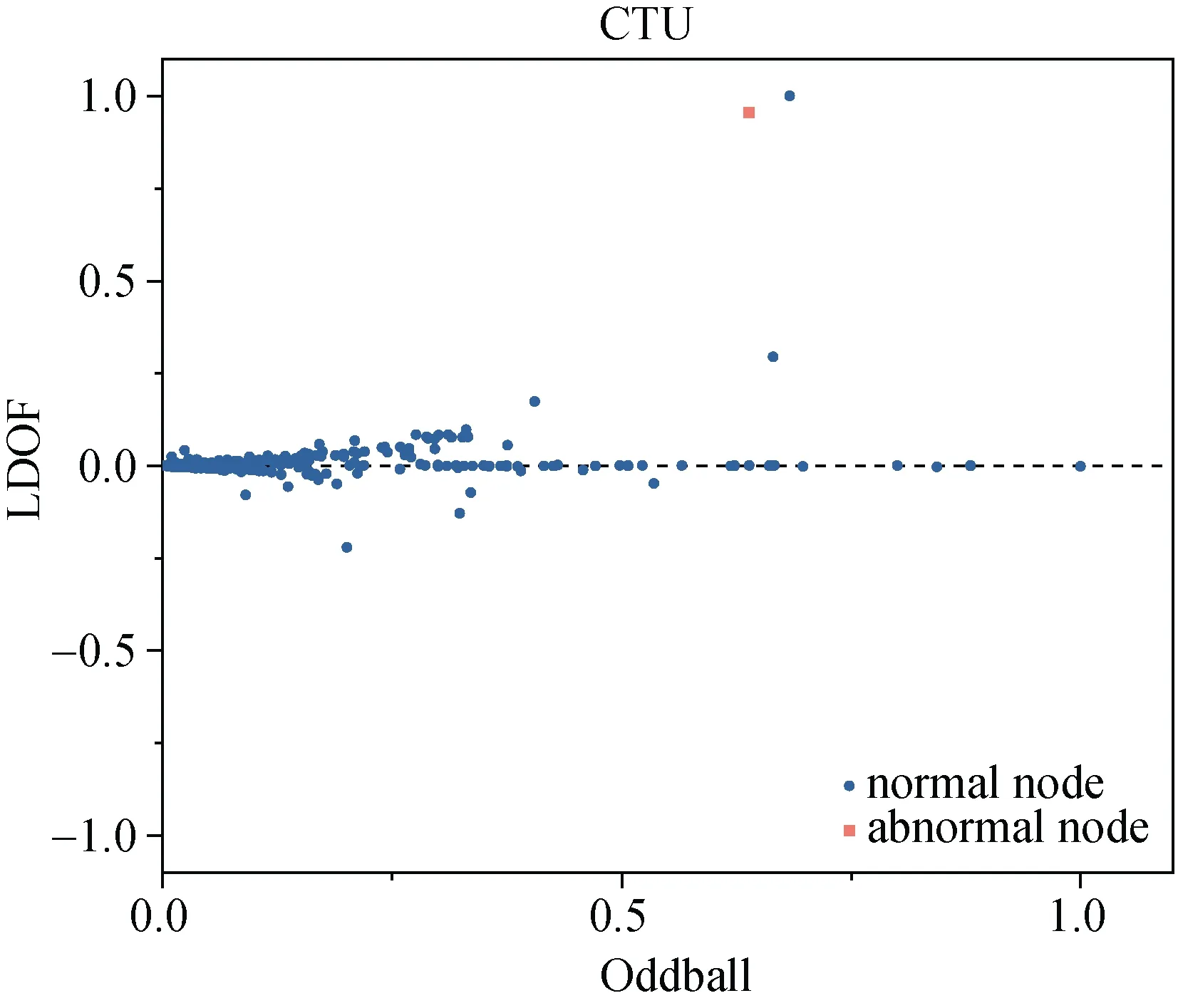
在上图9中, 蓝色数据点代表正常样本, 红色数据点代表所要检测的异常样本, 每个节点横坐标为对比方法Oddball及ANMFG对该节点异常程度进行 量化所分配的对应归一化异常分数, 纵坐标为LDOF为节点分配的对应归一化异常分数。由于Oddball方法仅考虑节点在网络中的一阶无向邻域结构, 因此其节点异常分数归一化后取值为[0,1], ANMFG虽然考虑了行为方向, 但未对节点子图异 常类型进行区分, 仍归一化为[0,1], 这两种对比方法都是异常分数越大, 节点所代表的用户异常程度越高。而本文的LDOF方法无向结构上进一步考虑了行为方向性, 因此其节点异常分数归一化后取值为[–1,1], 节点异常分数绝对值越大, 节点邻域中邻居节点间相互越疏离, 节点所代表的用户越可能存在异常。而其异常分数的符号进一步表明了异常类型信息, 异常分数符号为正, 代表节点邻域的行为呈现由节点向外发散趋势, 反之, 代表节点邻域的行为向节点呈现集中趋势, 据此可以进一步区分目标节点是采取异常行为的恶意节点, 还是被恶意节点进行攻击的目标节点。根据上图数据可发现, 本文LDOF方法相比Oddball方法及ANMFG方法在预先设定的L值条件下在以上两个真实数据集上指标衡量精度更高, 且在实际应用中, LDOF相比以上两种方法也可以更好地将异常用户节点从正常节点中区分开来, 且可以表明用户的异常性质。具有更强的异常检测能力。

5 总结

近年来, 基于结构特征的图异常检测算法由于其简单高效, 异常可解释性强等特点而备受关注。现存方法大多从无向网络结构出发, 通过提取节点一阶或二阶子图结构特征构建特征空间, 在此基础上进行离群点检测以挖掘异常结构。但在特征空间上的相邻节点, 可能在物理空间上并没有实际联系, 忽略了节点实际联系以及连边方向特征使其异常检测精度仍待提高。本文从节点实际连接关系出发, 利用模体结构对连边关系与方向特征转化为对节点间非对等联系的度量, 并在此基础上抽象为节点一阶子图密度, 运用基于密度的异常检测方法在实际网络结构中挖掘异常子图结构。通过在存在4种不同异常的合成网络以及存在真实异常的实际网络中进行实验, 实验结果表明该方法可有效挖掘异常子图结构, 且面对不同异常具有较高的鲁棒性。

本文仅从网络拓扑结构信息对网络中异常用户进行挖掘, 虽具有较好的异常检测效果, 但未考虑节点属性特征及行为属性特征, 如用户属性信息及文本内容信息等。虽然该类特征可能存在虚假或缺失信息影响异常检测精度, 且容易被异常用户伪装, 但结合结构信息不易伪装, 真实可靠的特点, 可以克服这一缺陷。如何综合这类特征, 在基于结构特征的异常检测方法上做进一步扩展, 共同对异常用户进行挖掘, 是下一步需要进行深入研究的方向。