图深度学习攻击模型综述

任一支, 李泽龙, 袁理锋, 张 祯, 朱娅妮, 吴国华

杭州电子科技大学网络空间安全学院 杭州 中国 310018

1 引言

随着人工智能的不断发展, 深度学习模型被广泛地应用在不同的领域中, 例如语音识别, 图像识别, 文本翻译等。图深度学习是深度学习在图结构数 据领域中的重要研究方向, 但在将数据建模为由点和边组成的图结构的社交网络、推荐系统等领域, 其应用仍然面临诸多安全问题。恶意用户通过攻击图深度学习模型往往能获得巨大的经济利益。例如在金融欺诈检测的场景中, 由于交易行为通常发生在高信誉用户之间, 因此信用评估模型往往利用此规律评估用户的信用度。而低信用的欺诈者通过与其他高信用者进行交易, 可使模型误判欺诈者信誉度, 并骗取高额信贷[1]; 在恐怖分子检测的场景下, 警方利用已认定恐怖分子间的通话记录来推断嫌疑人的身份。如两个恐怖分子与一个嫌疑人都与某用户进行过通话, 则警方会认为, 嫌疑人大概率是恐怖分子。而嫌疑人可通过隐藏共同通话记录躲过模型的检测。因此, 解决图深度学习模型的安全问题十分有意义。

现有图深度学习安全性问题研究主要包括攻击研究和防御研究。攻击研究模拟对真实系统的攻击过程, 目的是发现系统中潜在的安全威胁; 防御研究则是针对常见的攻击, 设计训练健壮模型的方法。攻击研究作为防御研究的前置步骤, 对后续的模型安全性的评估和防御工作有重大影响。与深度学习领域的攻击研究相比, 图深度学习攻击研究具有一定的特殊性, 主要是攻击手段和攻击模型构建方法的区别。从攻击手段看, 图深度学习攻击多采用对图结构数据中的点、边进行操作, 修改整体数据结构进而间接影响节点的特征的手段。而深度学习则是通过直接对数据的特征向量进行操作, 以达到攻击效果。从攻击模型构建方法来看, 构建图深度学习的攻击模型难度更大, 因为修改节点/边本质上是一种离散的操作, 因此通常需要将离散的选择问题连续化并构建攻击模型, 而这是一般的深度学习攻击模型构建过程中不需要考虑的。图深度学习攻击的特殊性也给该领域的研究带来困难与挑战。由于图数据呈现离散的状态(数据由节点表示, 数据之间的关系由连边表示), 因此在图深度学习攻击研究中, 最大的难点在于如何将节点(边)的选择表示为能对图深度学习模型损失函数造成影响的连续模型, 即如何将离散的邻接矩阵建模到连续的损失函数中。

自2018年Zügner等[2]提出图深度学习模型对抗的概念以来, 研究者们提出大量针对不同场景的攻击方法[3]。本文汇总现有图深度学习模型攻击的工作, 提出了一个统一的、全面的图深度学习攻击分析理论框架。理论框架有助于研究者能够快速理清、重现攻击模型, 并便于研究者设计新的攻击模型。

针对图深度学习中对抗性攻击问题, 本文首先介绍了不同图结构数据。然后, 对图深度学习模型攻击分析理论框架的结构进行详细介绍, 并围绕框架中预备阶段、攻击算法设计阶段、攻击实施阶段, 对现有的攻击方法进行了分析。最后, 对攻击模型中常用的数据集进行汇总, 并对图深度学习对抗领域现有的挑战以及未来可能存在的研究点进行总结。

2 图结构数据分类

图结构数据G=(V,E)被定义为由节点集和连边集构成的网络。根据节点和边的特点可将图划分为以下类型:

同构图与异构图:同构图与异构图[4]根据图的结构特征进行划分。同构图是指在整张图中仅有一种类型的节点和连边; 异构图指在整张图中包含多种类型的节点和连边。

动态图和静态图:动态图和静态图[5]根据图是否随时间变化进行区分。静态图是指节点和边不会随着时间的变化改变; 动态图是指在不同时刻, 节点或者边的分布不相同。

有向图和无向图:有向图和无向图[5]根据图中连边是否存在指向关系进行划分。有向图指连边存在方向, 比如在微博中存在的单向关注关系; 无向图是指连边不存在方向, 如社交网络中, 用户之间的好友关系。

有权图和无权图:有权图和无权图[5]根据图中连边是否等价进行划分。有权图也称为加权图, 指连边具有权重的图; 无权图是连边不具备权重的图。通常, 有权图中的边可根据不同权重进行区分; 而无权图中的边彼此之间并无差别。

3 通用图模型攻击流程框架

本文通过对现有图深度学习模型攻击的工作进行汇总分析, 提出了一个有助于研究者设计攻击模型进行参考的图深度学习模型攻击分析理论框架(如图3所示)。该框架将攻击过程分为三个阶段: 预备阶段, 攻击算法设计阶段和攻击实施阶段。

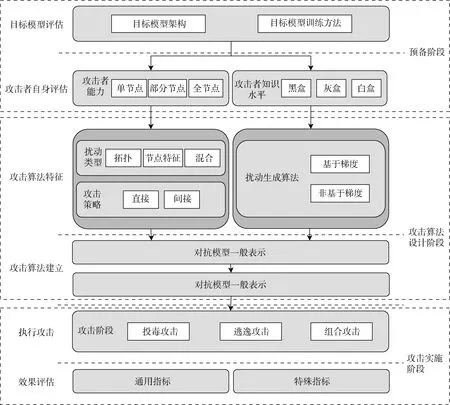
图3 图深度学习模型攻击分析理论框架 Figure 3 Graph deep learning model attack analysis theoretical framework

3.1 预备阶段

预备阶段是执行攻击前, 攻击者整合必要信息的阶段。在该阶段中, 攻击者需要对目标模型和攻击者自身进行评估。其中, 目标模型的评估工作包括对目标模型架构、目标模型训练方法等信息的整理; 攻击者自身的评估工作包含对攻击者知识水平的评估以及对攻击者能力的评估。

3.1.1 目标模型评估

1) 目标模型的架构

一般的深度学习中, 可以将模型的架构分为2种: 基于Pipeline的模型架构和基于端到端的模型架构[6]。

(1) Pipeline架构: 此类架构将问题分解为多个子任务, 并针对每个子任务设计不同的模型, 最终得到原始任务结果。见图1所示。

图1 Pipeline架构模型 Figure 1 Pipeline architecture

(2) 端到端架构: 此类架构使用一个模型解决原始任务, 模型的输出就是最终结果。见图2所示。

图2 端到端架构模型 Figure 2 End to end architecture

在攻击研究中, 由于Pipeline架构模型由多个子模型组成, 因此成功干扰其中一个子模型便能对整体结果产生巨大影响, 执行攻击的难度相对较小。而端到端模型仅包含一个模型, 攻击者的入手角度有限, 攻击难度更大。

2) 目标模型的训练方法

根据训练模型包含标签的情况, 目标模型采用不同的训练方法, 分别为: 监督学习, 无监督学习和半监督学习[7]。

(1) 监督学习: 利用包含标签的样本训练模型。典型的监督学习任务是回归任务和分类任务。

(2) 无监督学习: 利用无标签且类别不同的样本训练模型, 由模型生成样本的标签。典型的无监督学习任务是聚类任务。

(3) 半监督学习: 利用包含标签和无标签的样本共同学习模型, 无标签样本通过模型生成对应的标签。典型的半监督学习任务包括回归任务和分类任务。

三种学习方法的区别在于: 监督学习仅利用包含标记的样本训练模型; 无监督学习仅利用不包含标签的样本训练模型; 半监督学习同时利用两种数据训练模型。多数的应用场景中只知道部分数据的标签信息, 因此半监督学习方法的适用性更加贴合真实场景。

3.1.2 攻击者自身评估

攻击者自身评估指攻击者对自身知识水平和数据操作能力的评估。攻击者自身评估结果影响攻击算法设计阶段中的扰动生成方法, 自身知识水平影响扰动生成方式; 操作能力影响攻击模型中的扰动类型和攻击策略。

1) 攻击者能力评估

通常认为攻击效果与受到影响的节点/连边数量呈正相关。根据攻击者操作目标数由少到多, 将攻击者能力划分为单节点、部分节点、全部节点。

(1) 单节点

单节点攻击者对数据的操作权限最小, 只能改变图数据中某一特定节点的属性或者拓扑情况。如在社交网络推荐中, 攻击者不能操作其他用户, 只能通过改变自身的连边干扰预测模型。由于仅能操作单个节点, 攻击者通常会在图中寻找最具影响力的节点进行攻击[8]。

(2) 部分节点

部分节点攻击者对数据操作能力大于单节点攻击者, 其能操作图中部分节点和连边构成的子图。一般来说, 可操作的子图包含目标节点在内的n跳邻居, 攻击者在该子图中寻找代价最小的目标集合作为扰动样本[9]。

(3) 全节点

全节点攻击者对数据操作能力最大, 能操作全图中的节点或边。全节点攻击者需要在一定的代价内, 从全图中选择出的最佳的对抗样本。

通常, 攻击者不具备对全图的操作能力, 因此单节点攻击和部分节点攻击最贴近真实攻击场景。由于操作节点个数受到限制, 大多数单节点攻击和部分节点攻击得到的是局部优解。而全节点攻击利用全图的信息并从中寻找全局最优解, 因此其造成的破坏也最大。但从执行难度来看, 单点攻击和部分节点攻击成本更小, 攻击者更容易达到攻击的限制条件, 使其威胁更大。

2) 攻击者知识水平评估

本文将攻击者的知识水平从低到高分为黑盒攻击、灰盒攻击、白盒攻击。

(1) 黑盒攻击

黑盒攻击(Black-box attack, BA)者掌握的知识最少。在黑盒知识水平下, 攻击者不清楚模型架构、参数及训练数据等信息, 只能获取少量的模型反馈信息。Dai等[1]将黑盒攻击进一步划分为实用黑盒攻击(Practical black-box attack, PBA)和限制黑盒攻击(Restrict black-box attack, RBA)。实用黑盒攻击指攻击者仅了解模型的输出结果, 其中了解各类标签输出概率的实用黑盒攻击称为概率黑盒攻击(Confidence practical black-box attack, PBA-C), 了解输出标签的黑盒攻击称为离散黑盒攻击(Discrete practical black-box attack, PBA-D)。限制黑盒攻击指攻击者仅了解有限的模型输出反馈。

(2) 灰盒攻击

灰盒攻击(Gray-box attack, GA)者掌握知识多于黑盒攻击者。灰盒知识水平下, 攻击者掌握目标模型的部分信息。根据攻击者掌握的模型细节及数据情况可分为两种: 一是攻击者掌握部分模型细节。如文献[2]中, 攻击者清楚模型架构及部分参数细节, 但不掌握训练数据; 二是攻击者掌握模型的训练数据, 文献[10]将其进一步划分为掌握全部训练数据和掌握部分训练数据。

(3) 白盒攻击

白盒攻击(White-box attack, WA)者掌握最多的模型知识。白盒知识水平下, 攻击者充分了解目标模型的细节及训练数据。攻击者能利用模型结构, 参数和训练过程等信息设计有针对性的攻击方法。目标模型对白盒攻击者是透明的, 因此攻击者能采用的攻击策略也最丰富。

综合来看, 黑盒攻击执行难度最大, 威胁性也最大。由于其不需要攻击者掌握过多的模型知识和数据便能达到攻击效果, 多数的攻击者都能利用黑盒攻击方法干扰模型。相对的, 白盒攻击的效果最好, 但攻击需求知识最多。因此, 真实场景下很少出现白盒攻击者。同时, 通常将白盒攻击者假设为模型建立者, 攻击目的是提升模型的鲁棒性而非影响真实系统的运行, 因此白盒攻击的威胁性相比于灰盒/黑盒攻击更低。灰盒攻击的难度和威胁性介于两者之间。

3.2 攻击算法设计阶段

攻击算法设计阶段是图深度学习攻击分析理论框架的核心。攻击者根据预备阶段的信息设计攻击模型特征, 并利用模型特征对一般攻击表示进行修改, 得到特定场景下的攻击模型。攻击模型特征包含扰动类型, 攻击策略以及扰动生成方法。攻击者结合对图的操作能力设计扰动类型和攻击策略; 依据自身知识水平设计扰动生成方法。

3.2.1 算法特征设计

1) 扰动类型

攻击者通过向数据中添加不同扰动进行攻击。依据扰动类别的不同, 可将攻击分为图拓扑攻击、节点特征攻击和混合攻击。

(1) 图拓扑攻击

图拓扑攻击中, 攻击者专注于修改图中的连边来污染数据。依据攻击者对边的操作行为进行划分, 分为加边, 减边和重写三种攻击方式。

加边会改变节点的度、中心性等统计特征, 而添加固定的连边也会使得模型梯度上升, 如Wu等[11]攻击GCN模型, 提出一种基于梯度积分的攻击方法, 通过向图中添加使梯度上升最大的连边, 减缓GCN模型损失函数的梯度的下降速度。加边攻击的策略设计相对简单, 同时对攻击者的权限要求相对较低, 攻击策略的可解释性也比较好。但一旦添加的连边数量比较大时, 会显著改变图中的某些统计特征, 在抵抗基于统计特征的检测中加边攻击表现较差。

减边能切断与邻居节点之间的消息传递从而降低节点间的相似性。如Sun等[12]在论文合著网络上的减边攻击, 通过删除桥接不同社区的连边, 使得目标节点之间的相似性从0.67下降到0.37。类似地, 加边、减边也能影响梯度下降的速度, 如Chen等[13]通过删除GCN模型中对梯度下降贡献最大的边, 使得模型的损失下降过程变慢, 影响模型效果。相比于加边攻击, 减边攻击的执行效率要更高一些, 因为多数的图数据都是稀疏的, 已知的连边数量远远小于未知的连边数量, 故减边攻击候选的扰动空间通常小于加边攻击。当然, 减边攻击同样存在容易被防御模型检测的缺点。

重写攻击(Rewrite attack, RA)指对图中的连边同时执行增加、删除操作, 其增减连边的数量可以相同。2018年, Waniek等[14]提出一种可扩展的启发式重写攻击ROAM。ROAM将攻击过程描述为两个步骤, 首先删除目标节点与其度数最大的邻居节点间的连边, 之后建立目标节点与其度数最小的k–1个邻居节点间的连边。在2019年, Chen等[15]提出针对社区检测的启发式攻击, 每轮攻击中对一阶邻居节点间的连边进行成对增减。同年, Ma等[16]改进一阶邻居选择策略, 利用强化学习选择需要修改的一阶和二阶邻居连边替代仅修改目标节点一阶邻居的连边, 提升了攻击的隐蔽性。Takahashi等[17]进一步优化邻居的选择过程, 提出一种修改m阶邻居的拓扑结构的方法POISONPROBE。POISONPROBE通过构建内外层循环函数和参数化的方法, 将连边选择问题连续化为可利用梯度求解的连续优化问题。其中, 内层循环在一组参数控制下寻找局部的较小扰动; 外层循环外循环通过使用二进制搜索迭代地更新全局控制参数λ, 当全局控制参数λ小于定值时输出扰动结果。重布线增减的连边数量也可以不同, 如文献[1,13]等选择每一轮模型中对梯度影响最大的连边作为候选扰动, 每一轮修改的连边数量并不固定。重写攻击通过减小加边、减边对统计特征的干扰, 克服了加边、减边方法容易被检测的困难, 提升了攻击的隐蔽性。但是重写攻击的时间成本显著增加, 攻击者需要同时从加边、减边的候选集合中选择的扰动, 其复杂度是加边、减边策略之和。

(2) 节点特征攻击

节点特征攻击中, 攻击者专注于修改图中节点的特征来污染数据集。在图深度学习中, 节点特征嵌入完成前, 其表现形式通常为离散矩阵X∈ { 0, 1}N×D, 攻击者可直接翻转对应位置的特征值达成攻击目的[10]; 嵌入完成后, 离散的特征矩阵转化为连续形式X∈ℝN×K, 攻击者可以直接在连续值上添加扰动来进行攻击[18]。特征攻击的策略更加直接, 但是其可解释性也更差, 难以在真实场景中得到应用。即使可以找到实际应用场景, 但很少有攻击者能直接操作数据中节点本身的特征, 除非该攻击者具备极高的权限, 因此该假设在实际攻击中几乎不能成立。

(3) 混合攻击

混合攻击中, 攻击者结合图拓扑与节点特征来增强攻击效果。根据是否修改已经存在的连边, 可将混合攻击分为两种: 一是注入节点, 攻击者构造注入节点的连边和特征, 并添加到原始图中。如Hou等[19]针对异构图上的异常节点检测问题提出HG-ATTACK方法, 通过构造辅助软件并将其注入到软件下载异构图中, 使得检测模型无法识别目标恶意软件。二是直接在原始图上选择连边和节点特征进行修改。如Wang等[20]提出的Greedy和Greedy-GAN方法。Greedy方法通过计算候选连边和特征对梯度上升的影响, 贪婪地选择对梯度影响最大的节点特征和连边, 翻转后作为扰动注入原始图数据。Greedy-GAN借鉴GAN的思维对Greedy进行改进, 在Greedy模型的基础上添加了生成器和检测器模型, 由Greedy生成的扰动送至检测器模型进行真假判断, 在生成器和检测器的博弈过程中提升生成节点特征的真实性。Zou等[21]研究了文献[22]中抛出的针对黑盒逃逸场景的图注入攻击问题(GIA), 提出一种节点注入攻击方法TDGIA来提升攻击效果。TDGIA设计了拓扑缺陷边选择模块和用于注入节点属性生成的平滑对抗优化模块解决GIA黑盒逃逸问题。拓扑缺陷边选择模块利用原始图的拓扑漏洞来检测对攻击最有效的已知节点, 然后在该节点周围注入一定数量虚假节点。平滑对抗优化模块定义了一个损失函数来优化节点的特征, 以最小化受害GNN模型的性能。TDGIA相比于先前的节点注入方法, 解决了黑盒逃逸场景设置下, 投毒攻击方法效果不佳和无法处理大规模图数据的问题。同时, TDGIA针对顶级防御模型也有较好的效果。混合攻击的优势在于, 攻击者添加极少的注入节点或者修改少数连边和节点特征就能对结果造成比较大的影响, 在攻击某个特定目标节点时表现优秀。特别是注入节点攻击, 攻击者能自由控制注入数量, 使得攻击具备可伸缩性, 同时保证原始图中已有连接关系不会被破坏。但当扰动限制较小时, 对受害模型整体效果的影响还有待考证, 且攻击者需要同时构建(计算)对结果影响较大的连边和特征, 计算复杂度较高。

总结三种攻击扰动类型各自的特点: a)图拓扑攻击中, 加边、减边会破坏原始图结构中的统计特征(如连边的总数), 容易基于此特征检测到攻击, 而重写攻击面对统计特征检测方法的隐蔽性更高; b)节点特征攻击对权限要求较高, 在真实的攻击场景下难以执行; c)混合攻击策略中, 在原始图上寻找候选扰动的代价较大。而注入节点攻击代价较小且具备可伸缩性, 且能保证原始图中已有连接关系不会被破坏, 但构建虚假节点特征和连边的计算复杂度较高。

2) 攻击策略

攻击者需要根据自身操作能力选择合适的攻击目标。依据操作目标, 将攻击策略分为直接操作和间接操作。

(1) 直接操作

直接操作是指攻击者将扰动直接添加到目标节点上。即攻击者可以通过直接修改测试节点的特征[23]; 或修改目标节点的连边关系[13], 误导模型对某节点的预测结果。

(2) 间接操作

间接操作是指攻击者将扰动添加到目标节点的邻居上, 利用图中节点间的信息传递, 使目标节点受到干扰。根据邻居节点的选择情况, 可分为操作一阶邻居和操作多阶邻居。如文献[24]对一阶邻居的拓扑结构执行重写攻击; 文献[16-17]对m阶邻居拓扑结构重写攻击, 提升了攻击的隐蔽性。

直接操作的缺陷在于, 攻击目标往往是受到严密保护的重要节点, 使得直接攻击容易被发现。间接操作攻击有效利用图模型中的信息传递的特性, 解决了对布防节点添加扰动的问题, 同时提升了攻击的隐蔽性。

3) 扰动生成方法

扰动生成方法影响模型求解最佳扰动的效率及计算难度。现有工作中, 依据不同的攻击者知识水平, 可将扰动生成方法分为两类: 基于梯度和基于非梯度的扰动生成方法:

(1) 基于梯度的扰动生成方法

基于梯度的方法适用于白盒攻击场景, 或灰盒攻击中, 攻击者能训练一个替代模型来进行攻击的场景。在图深度学习中, 模型训练的本质是参数顺着损失函数梯度下降的方向更新的过程, 因此攻击者计算对抗样本对目标模型梯度的影响, 并选择影响梯度下降结果的扰动。

Dai等[1]最早采用梯度方法求解扰动, 提出RL-S2V和GradArgmax算法。假设攻击者具备白盒知识水平, 在模型的训练过程中计算梯度变化矩阵, 对梯度变化影响最大的一组边进行增删。为了优化计算效率及效果, 后续研究者对梯度方法进行逐步优化。Xu等[25]提出PGD攻击方法, 结合谱图理论、一阶优化和稳健(最小-最大)优化的理论, 将梯度投影到一个连续的空间中, 通过优化离散梯度的近似表示对梯度计算过程进行优化, 解决了梯度饱和带来的次优解问题。Xu等[26]为解决攻击GNN模型时计算离散梯度困难的问题, 提出GTA攻击方法, 每次选择n条边替代全图边的梯度计算, 大大降低了梯度更新计算的复杂度。Bojchevski等[27]针对半监督节点嵌入方法(如Deepwalk、随机游走等)模型不连续造成的梯度计算困难问题, 提出一种通用攻击方法。该方法首先利用半监督模型的嵌入过程将攻击模型中的双层优化问题转化成单层优化问题。再通过将嵌入矩阵通过SVD分解为邻接矩阵及两个特征矩阵, 并将分解结果带入单层优化模型并将其转化为一个线性优化问题。最后通过计算邻接矩阵的变化求解使得最大化的扰动连边。Gupta等[28]对Bojchevski的攻击方法进行了改进, 提出VIKING攻击方法简化模型并提升了攻击效率, 同时提升了攻击效果。他们通过自定义一个与邻接矩阵相关联的影响力函数求解增删连边对节点嵌入结果的影响, 将原本的双层优化问题转化为最大化影响力的问题。VIKING在限制修改连边数量的约束下, 在每轮影响力计算中翻转影响力最大的连边, 使得嵌入模型效果变差。Wang等[29]提出一种近似快速梯度符号的算法, 通过将GCN模型的损失函数近似为0-1线性特征和边缘0-1向量的关系, 通过梯度最小化新的损失函数得到近似解, 从而解决离散梯度计算困难问题。Wu等[11]对离散优化问题的梯度计算过程进行优化, 提出一种基于梯度积分的选择扰动边的方法。使用梯度积分可以准确计算翻转离散边或特征引起的模型变化, 与先前攻击模型使用的迭代方法相比, 大大提高了节点和边缘选择的效率和准确性。Zhu等[30]认为基于图的异常检测系统OddBall在实际应用中存在脆弱性。他们提出一种基于梯度的攻击方法BinarizedAttack, 目的是通过操作图拓扑结构提升OddBall系统对节点异常得分值计算的误差。BinarizedAttack借鉴了BNN的思想, 为图中的每条边/非边关联了一个离散和一个连续的决策变量, 两个决策变量分别在前向传播和反向传播中起作用。在前向传递中, 离散决策变量用于评估目标函数; 在反向传播中, 首先根据分数梯度更新连续决策变量, 然后相应地更新离散决策变量。BinarizedAttack设计的这种新的梯度下降计算方法, 很好的解决了离散的双层优化问题难以计算和计算结果过于复杂的问题。Chen等[31]提出一种基于梯度动量的攻击方法MGA, 通过求解梯度的方向动量替代以梯度的绝对值选择扰动边, 解决了结果陷入局部最优的问题。MGA的框架利用原始网络来训练代理GCN模型, 之后为损失函数计算每个链路的梯度并计算动量。选择梯度动量绝对值最大更新原始网络并迭代计算, 直到达到扰动代价上限。对于动态图上的攻击研究空缺, Chen等[32]提出一种针对动态网络链路预测任务的攻击的方法, 计算来自不同时间节点的动态网络嵌入梯度信息, 贪婪选择梯度绝对值最大的连边翻转, 通过在历史图数据上添加扰动, 完成对动态图的攻击。Geisler[33]等发现, 先前的图深度学习攻击模型普遍会利用邻接矩阵, 这造成这些方法无法在实际的大规模图数据上使用。为了解决这个问题, 他们提出了两种基于一阶优化的不使用邻接矩阵的攻击方法GANG和PR-BCD。GANG通过在目标节点周围注入节点, 执行基于约束梯度的优化, 以确定给定代价下的最佳扰动边, 并采用PGD优化新节点的初始特征(随机采样)。PR-BCD基于随机块坐标下降(R-BCD)在现有节点之间添加/删除边, 将增删边的问题建模为L0范数PGD和随机块坐标下降(R-BCD)的自适应组合的问题, 在每轮迭代中保留候选搜索空间, 并对其余部分重新采样进行次轮迭代。Miller等[34]提出了最短路径攻击问题, 即攻击者意图通过删除最少的边, 使得两个目标节点之间的最短路径能通过某条期望路径。他们将NP难的路径切割转化成加权集覆盖问题, 并提出两个最小化总代价的优化方法PATHA- TTACK-Greedy和PATHATTACK-LP求解优化问题。PATHATTACK-Greedy通过迭代添加最具成本效益的子集(每个成本中未覆盖元素数量最多的子集)寻找候选连边集合; PATHATTACK-LP将整数约束放宽为实数并对结果进行四舍五入, 解决了离散域上的优化求解困难。Tian等[35]的研究发现FGA和NETTACK存在忽略注入节点之间的互相影响, 在固定的扰动预算下, 不能保证所有目标节点的全局攻击成功率的问题。针对该问题, 他们提出改进方法P-FGA和P-NETTACK。两个改进方法应用了节点过滤机制, 从目标节点集中过滤掉那些被成功攻击的节点, 同时在提取常见扰动后, 还利用随机的扰动补充攻击预算。同时, 还利用新的损失函数CW-loss代替FGA中CE-loss, 并将代理损失的最大总和作为新的目标函数, 以支持P-FGA和P-NETTACK集成统一的并行计算框架。Zhan等[36]研究了Mettack等传统灰、黑盒图深度学习攻击模型的特点, 发现传统方法存在需要访问训练数据以建立攻击模型的缺陷。他们提出首个在不访问训练数据的情景下的梯度攻击方法BBGA。BBGA利用谱聚类生成的伪标签来训练代理模型, 解决了不能访问训练数据的真实标签问题。同时, BBGA采用一种k-折贪婪策略, 将所有节点分为k组, 并定义每对节点的元梯度标准差和为连边的贪婪分数, 每轮迭代中选择贪婪分数最大的边作为候选边, 解决了大多数传统攻击不能将扰动均匀分布到原始的训练数据中的问题。

基于梯度的求解方法能够保证得到局部最优解甚至全局最优解, 就攻击效果而言是所有方法中最好的。但是基于梯度的方法也存在一定限制。首先基于梯度的方法要求攻击者具备能支撑建立损失函数的知识, 要求相对较高。其次, 在建立梯度模型的过程中存在比较多的困难, 如离散问题连续化和离散优化问题求解, 虽然已经有较多的研究者对这些挑战进行研究并提出应对方法, 但是大多数解决方案得到的是近似结果, 仍然存在一定误差。同时, 梯度计算的困难程度还和数据规模呈正比, 这就意味着, 一般规模数据下采用梯度方法的复杂度还是可以接受的, 一旦数据规模增大, 其复杂度会呈现指数级增长, 而这对于现实场景中日趋庞大的图数据规模显然是一个巨大的难题。

(2) 基于非梯度的扰动生成方法

基于非梯度的攻击适用于黑盒攻击场景, 或在灰盒攻击中, 攻击者无法建立替代模型进行攻击的场景。攻击者通常采用启发式、遗传算法或强化学习的方法替代计算梯度来求解扰动集合。

a) 启发式方法

图深度学习模型攻击中, 启发式方法通常指根据图的统计特征构造扰动样本。如改变度分布, 降低两个节点之间的相似度, 进而影响模型结果。

最简单的启发式攻击通过在节点之间随机增删连边来改变图的拓扑结构, 或随机修改节点特征。如Chen等[15]攻击社区检测模型, 通过随机增删原始图数据的连边, 改变模型社区划分结果。同时, 他们提出针对不同目标的攻击方法CDA和DBA。CDA的攻击目标为社区中的随机节点, 删除与本社区中节点相连的边, 增加与其他社区中节点的连边; DBA攻击目标为社区中的度数最大的节点, 其增删连边的策略和CDA相同。结果显示两种方法都降低了社区检测模型的准确率。Xuan等[37]对无标度网络的分类模型进行攻击, 结合节点度数量和度分布设计了两种攻击策略DILR和DALR。首先根据度大小将节点分为三档, DILR删除度最大的一档节点与随机节点之间的连边, 并在两个随机二档节点间添加连边; DALR保证扰动添加前后网络的度仍然服从幂律分布, 删除大度节点之间的连边, 同时选择度数较小的节点添加连边。然而, 实际攻击场景下, 攻击者掌握的知识非常有限, Hussain等[38]提出一种基于结构的攻击方法Structack来解决这一问题。他们考虑更实际的攻击场景, 并假设攻击者仅具备图数据的结构知识, 探究节点的度中心性和最短路径相似度对GNN分类模型的影响。Hussain通过归一化理论将节点的度中心性和最短路径相似度建模到GNN模型中并通过计算梯度得到两者对GNN模型的影响程度, 结果表明低度中心性和低最短路径相似度节点更能影响GNN的准确率。依据此结论, Structack攻击方法即为低中心性以及低相似度的节点之间添加虚假连边。

启发式的方法通常从图数据的统计特征出发, 并对统计特征(如度、中心性、相似性等)存在特殊性的节点或边进行操作, 这令启发式攻击方式比较依赖图数据的分布。一旦图数据的分布发生比较明显的变化, 启发式方法的效果也会下降, 因此启发式攻击的可迁移性弱。但启发式攻击的优点在于算法简单, 往往能在很短的时间内生成大量的扰动样本, 在一些大规模的图数据上也能有不错的表现。

b) 基于遗传算法

图深度学习模型攻击中, 基于遗传算法生成扰动即, 上一轮生成的扰动作为亲代, 交换扰动生成子代扰动, 并通过评价函数筛选出符合条件的结果。

Dai等[1]最早将遗传算法用于求解扰动, 提出GeneticAlg算法。GeneticAlg算法选择能够增加目标函数损失的子图作为候选亲代, 子代样本保留亲代样本中相交的部分, 同时随机选择两亲代间不相交的部分作为剩余填充。GeneticAlg的突变部分则是采用概率随机变化的策略, 即交换的节点对中的一个以一定概率变化为亲代节点序列中的随机一个节点。迭代计算直到达到代价上限输出最后一轮中保留的子代作为攻击扰动。Chen等[15]针对社区检测提出Q-ATTACK攻击方法, 将扰动边组合作为遗传算法中的亲代基因, 以模块度Q作为适应性的评价函数。模块度Q较低的亲代扰动样本得以保留, 并交换单点基因产生新的子代扰动样本。为了防止解陷入局部最优, Q-ATTACK中提供三种变异方式: 链接删除、链接添加变异和链接重写。链接删除和链接添加属于单独变异, 链接重写则是共同变化, 且三种突变以相等的概率发生, 并用总突变率来控制。Chen等[9]对Q-ATTACK算法进行拓展与改进, 在不同对抗目标下采用不同的评价标准: 节点度变化衡量单目标攻击结果的适应性; “度变化+熵变化”衡量对整体模型的可用性攻击结果的适应性。同时提出了一种非对称交换遗传因子的方法, 增加了亲代对抗样本产生子代对抗样本的种类, 使得对抗样本生成更加灵活。Yu等[39]针对提出了一种欧几里德距离攻击(Euclid Distance Attack, EDA), 旨在直接干扰嵌入空间中向量之间的距离。EDA采用遗传算法求解扰动样本集, 使用空间中向量距离的相对变化来构造适应度k。EDA筛选k值较大的扰动样本作为亲代, 通过单点交换规则生成子代, 大大提升攻击的隐蔽性。

基于遗传算法的方法对图数据统计特征的破坏相对较小, 能够有效规避常规的检测模型。同时, 遗传算法计算效率和启发式方法类似, 收敛速度快。但基于遗传算法在数据规模较大时, 候选亲代数量会出现指数级增长, 使得计算复杂度增大。

c) 基于强化学习的方法

图深度学习攻击中利用强化学习生成扰动, 通常将当前状态定义为当前已有的扰动样本集, 动作定义为添加特定扰动, 对应奖励则与目标模型结果关联。强化学习生成扰动的过程可以描述为, 利用动作(添加特定扰动)更新当前状态(扰动样本集), 添加扰动使模型准确度下降则获得奖励。

Dai等[1]最早将强化学习应用于攻击图嵌入模型。攻击模型输入原始图数据, 强化学习的状态对应阶段t生成的扰动样本; 动作为增加/删除连边; 奖励与预测节点标签相关。若预测标签与原始标签不同则得到正向的激励, 相同则得到负向的激励。算法将选择扰动分解为两个动作, 每个动作选择原始图中的一个节点。Ma等[16]将重写攻击的过程视为在图数据上的离散马尔可夫决策过程, 并提出一种强化学习的方法ReWatt求解决策结果。ReWatt中, 状态被定义为生成扰动结果之前的所有中间结果, 动作定义为删除一阶邻居连边, 增加二阶邻居连边的重写操作。ReWatt使用GCN来学习每个中间状态的节点和边缘嵌入, 在执行一步重写操作之后, 查询黑盒分类器以获得下个中间状态的预测损失, 将其与当前状态的损失进行比较以获得奖励, 直到奖励达到最大值输出最终扰动。Sun等[40]基于贪婪策略行注入攻击, 并将RL-S2V算法的两步选择优化为三步选择: 第一步为选择注入节点; 第二步为选择原始节点并添加连边; 第三步为选择注入节点的标签。

强化学习是最近几年兴起的机器学习邻域, 该方法对求解离散优化问题有很好的效果。基于强化学习的攻击方法在不同的受害模型上都有较好的表现, 因此该类方法迁移性最高。然而, 强化学习的方法需要攻击者构建代理模型, 虽然对模型知识的要求小于基于梯度的方法, 但还是高于启发式和遗传算法。同时, 强化学习的动作选择空间限制了其计算效率和处理离散优化问题的规模, 当图规模较大时, 动作选择空间随之增大, 寻优过程复杂度增加, 造成强化学习方法求解真实场景中过大图数据时速度慢的问题。

总结梯度与非梯度方法的特点: a)基于梯度的方法的优势在于能保证结果的局部最优性。其缺点在于, 对攻击者的知识水平和权限要求较高, 要求攻击者有能力重建目标模型的损失函数。因此, 攻击者的目标通常是寻找到网络数据中比较敏感的节点加以保护。由于真实攻击场景中很难获得完备的知识及权限, 基于梯度的方法求解扰动比较困难。b)基于非梯度的方法的优势在于可迁移性好, 且算法相对简单, 计算复杂度更低。缺陷在于: 多数启发式算法和基于遗传算法的方法, 通过图的统计特征选择扰动, 隐蔽性较差。特别是启发式的方法, 还存在迁移性较差的问题。而基于强化学习的方法虽然具备较好迁移性, 但动作选择空间比较大, 寻优的过程相对复杂。

3.2.2 攻击算法建立

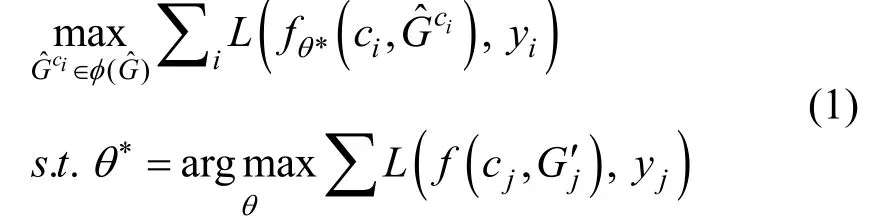
其中 ()f·表示的不同的图深度学习模型(如图分类模型、图预测模型、图嵌入模型等)。

需要注意的是, 攻击中不仅需要保证攻击的可行性, 还需要保证隐蔽性。即通过差异计算函数Q得到扰动添加前后图数据之间差异值, 当差异值小于定值ε时, 则认为攻击足够隐蔽:

另一个保证隐蔽性的方法是, 规定一个攻击代价Δ, 扰动总和小于代价Δ时, 则认为攻击不会被发现:

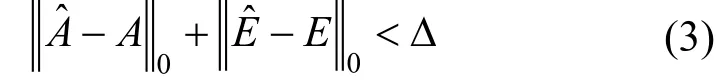
攻击者生成新的攻击模型, 首先确定一般表示中的图深度学习模型, 然后将模型特征转化为约束条件, 整合约束条件便得到新场景下的攻击模型。

3.3 攻击实施阶段

攻击实施阶段, 攻击者选择攻击执行的时间, 并在攻击结束后, 结合目标模型的任务对攻击进行评估。

3.3.1 执行攻击

不同时刻添加扰动会造成不同结果。依据攻击时目标模型所处的训练阶段, 将攻击划分为投毒攻击(Poison attack, PA), 逃逸攻击(Evasion attack, EA)和组合攻击(Combination attack, CA)。

1) 投毒攻击

投毒攻击是指攻击者在模型训练完成前进行攻击。投毒攻击者向训练数据集中注入扰动, 利用“污染”数据集训练模型。如Wang等[20]向推荐系统数据集中添加虚假评分数据, 提升了目标商品的推荐度; Wu等[11]增删训练数据中的连边并利用污染数据训练模型, 使模型准确率降低; Zhang等[41]攻击知识图谱嵌入模型, 替换知识图谱训练数据中三元组的首尾实体, 改变实体的嵌入表示, 进而降低实体预测模型的准确度。

2) 逃逸攻击

逃逸攻击是指攻击者在模型训练完成后向测试数据中添加扰动, 使得污染的测试数据在模型上结果出错。由于扰动添加在测试数据集中, 逃逸攻击仍使用“干净”数据集训练目标模型, 不会对模型本身造成影响。Chen等[13]攻击图嵌入模型, 构造扰动测试样本在原模型中得到错误嵌入表示, 并降低下游的节点分类准确度; Zhang等[18]意图规避基于图的恶意代码检测, 将恶意代码视为由语义信息组成的图数据, 向恶意代码中注入空语义, 使得恶意代码逃避检测。

3) 组合攻击

组合攻击是指攻击者向训练数据和测试数据中同时注入扰动来影响模型结果。Hou等[19]攻击基于图的恶意软件检测模型, 不仅向原始的训练数据图中添加“辅助”恶意节点, 还对测试样本中的恶意软件的特征和结构特征进行修改, 使得检测模型误判恶意软件为正常软件。Zhang等[42]研究了图分类中的后门攻击(Backdoor attack, BA), 通过构造一个特殊结构的子图(触发器)并赋予标签, 将其注入训练数据中, 模型会学习触发器与标签的对应关系。将触发器插入测试样本, 使得分类模型将测试样本分类为特定的类别。Xi等[43]也探究了图分类上的后门攻击, 并证明后门攻击在隐蔽性上有很好的表现。

从不同角度进行分析, 三种攻击各有优势: a)影响范围来看, 逃逸攻击本质上不改变模型, 攻击只会改变添加扰动的测试样本的结果; 投毒攻击和组合攻击会改变模型, 影响范围更大, 威胁也更大; b)从攻击操作的复杂程度看, 投毒攻击属于一种“一劳永逸”的攻击方式, 而逃逸攻击、组合攻击需要攻击者在每次攻击前向目标注入扰动, 相对与投毒攻击执行过程更加繁琐; c)从攻击执行条件上看, 由于获得训练数据的代价较大, 因此投毒和组合攻击花费的代价更大; d)从攻击的隐蔽性来看, 投毒攻击使大量测试样本结果出现偏差, 攻击容易被察觉; 逃逸攻击和组合攻击针对特定样本攻击, 攻击不易察觉; e)从攻击效果上来看, 多标签分类任务中, 大部分投毒、逃逸攻击不能使目标被分类为指定类别, 而组合攻击中的后门攻击能误导模型将目标分类为指定类别。

3.3.2 攻击效果评估

攻击完成后, 攻击者需要对攻击结果进行评估, 以评判对抗样本的优劣。从适用范围来看, 可将评价指标划分为通用指标和特殊指标。

1) 通用指标

(1) 攻击成功率

攻击成功率(Attack success rate, ASR)表示成功的攻击次数占全部攻击次数的比例, 主要用来衡量攻击算法生成的扰动效果好坏。攻击成功率越高表示攻击算法效果越好。攻击成功率是图对抗研究中应用最多的评估指标之一, 计算表达式为

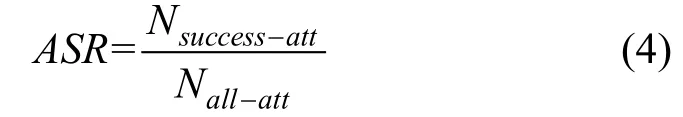
其中Nsuccess-att表示攻击成功的对抗样本数量,Nall-att表示所有对抗样本数量。

(2) 目标模型准确率

模型准确率(Accuracy)表示结果正确的样本数占全部测试样本数量的比例, 用来衡量攻击目标模型效果的好坏, 目标模型的准确率越低证明攻击越有效。计算表达式为

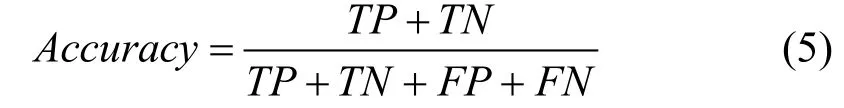
其中TP和TN分别表示真正例和真负例的数量,FP和FN分别表示假正例和假负例的数量。

(3) 平均扰动连接数量

平均扰动数量(Average modified links, AML)表示攻击成功的情况下, 修改连边数量的平均值。该指标引用与图拓扑攻击中, 主要用来衡量攻击代价。AML的值越高则攻击者成功执行攻击需要的代价越大。计算表达式为:

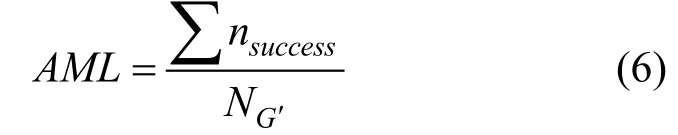
其中nsuccess表示攻击成功的对抗样本修改的连边数,NG′表示对抗样本的数量。

(4)F1值

F1值(Macro-F1)表示精确率(Precision)和召回率(Recall)的加权平均。不同模型的F1值能衡量不同的攻击性能。如Wang等[20]以虚假节点检测器的F1值衡量攻击的隐蔽性, 检测器的F1值越高则扰动的隐蔽性越好; Yu等[39]用目标模型的F1值衡量扰动的攻击效果, 目标模型的F1值越低则攻击效果越好; Hou等[19]利用恶意软件检测器的F1值衡量模型攻击效果, 其F1值越小则攻击效果越好。F1值的计算表达式为:

其中TP和TN分别表示真正例和真负例的数量;FP和FN分别表示假正例和假负例的数量。

(5) 分类边界

分类边界(Classification margin, CM)表示节点被分类为正确类别的概率与被分类为错误类别的最大概率之差。对分类模型来说,CM越大证明分类准确度越高; 对攻击者来说,CM的值总和越小则攻击效果越好。分类边界计算表达式为:

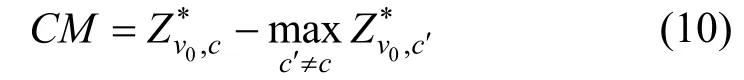
其中c表示目标节点的真实标签,Z0,vc*表示图模型分类正确的概率。分类边界的值可以小于0, 此时表示节点被错误分类。

(6) 分类错误率

分类错误率(Misclassification rate, MR)表示分类错误的样本个数占全部测试样本的比例。对攻击者来说, 目标模型的分类错误率越高则攻击效果越好。文献[11,23,25,29,27,44]采用此指标衡量扰动效果。分类错误率的计算表达式为[23]:

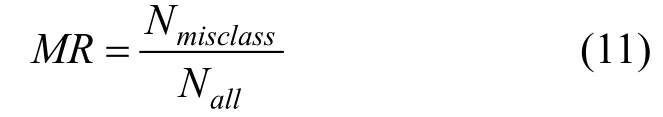
其中Nmisclass表示错误分类的样本数量,Nall表示全部测试样本数量。

(7)AUC值

AUC值表示ROC曲线下的面积, 用于衡量目标模型效果。图深度学习模型中,AUC值越接近1, 则模型效果越好。文献[45-47]利用AUC值来衡量扰动对目标模型的攻击效果,AUC值越低攻击效果越好。Lin[47]等攻击基于GCN的链路预测模型, 并将AUC值下降到0.1以下。

(8) 归一化互信息量

归一化互信息量(Normalized mutual information, NMI)结合互信息和信息熵, 计算出两个聚落之间的相似度。在社区检测任务中, NMI的值越大则社区检测模型效果越好。对攻击者来说, NMI的值越小则攻击效果越好。文献[9,15,39]等对社区检测模型进行攻击, 其结果都显示能将NMI的值降低至0.5以下。计算表达式为[15]:

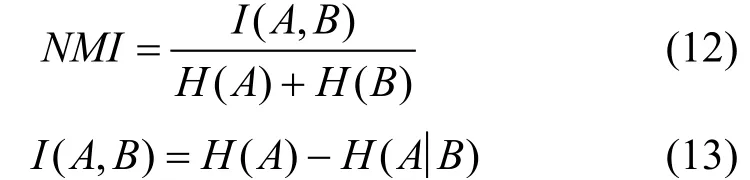
其中H(A) 和H(B)分别表示A和B的信息熵,I(A,B)为两社区的互信息。直观上,A和B越相似, 互相能提供的有用信息越多,H(A|B)越小。

2) 其他指标

(1) 添加的虚假节点的数量

添加虚假节点数量(Add fake node num, AFNN)用来描述攻击代价大小, 值越小则攻击者的代价越小, 应用于添加虚假节点的攻击方法[20]。

(2) 攻击隐蔽性度量

攻击隐蔽性度量由三个指标组成, 分别为: 平均距离相对变化(Relative change of average distance, ΔL)、平均聚类系数相对变化(Relative change of average clustering coefficient,CΔ )、对角线距离的相对变化(Relative change of diagonal distance,DΔ )[37]。三个指标均能表示扰动添加前后图结构的变化程度, 主要用于衡量针对无标度网络的攻击的隐蔽性。三个指标越小表示添加扰动前后图结构的变化越小, 攻击越隐蔽。Xuan等[37]在无标度网络的攻击中, 利用上述三个指标控制扰动连边的数量。

平均距离相对变化表示扰动添加前后最短路径长度的平均值之差, 与原始网络最短路径长度平均值的比值。计算表达式为[37]:

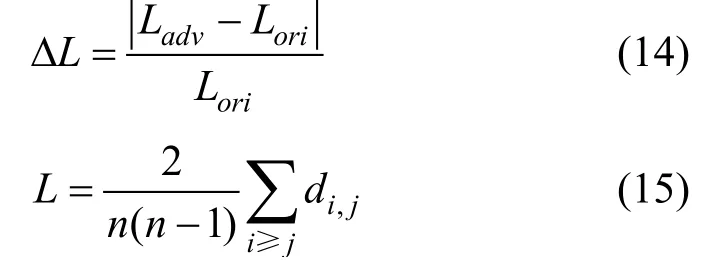
其中n表示图中节点个数,di,j表示节点vi,vj之间的最短路径。

平均聚类系数相对变化表示扰动添加前后平均聚类系数之差, 与原始网络平均聚类系数的比值, 反映了节点邻居之间的紧密程度。计算表达式为[37]:

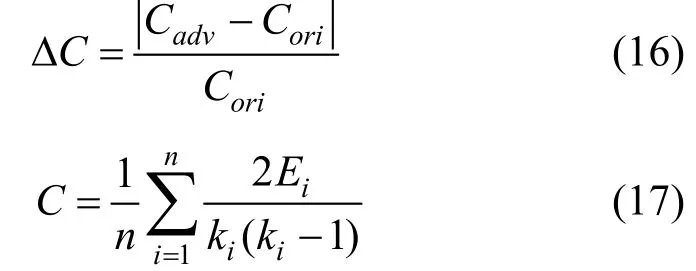
其中ik和iE分别表示节点iv的邻居节点数量和邻居连接数量。

对角线距离相对变化表示扰动添加前后对角线距离之差与原始对角线距离的比值。其计算表达式为[37]:

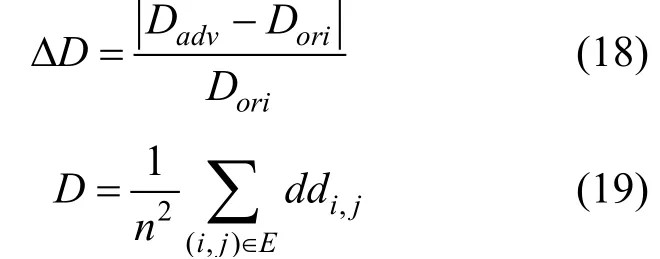
其中ddi,j表示邻接矩阵A中元素i,j到主对角线的距离。

(3) 正精度下降

正精度下降(Benign accuracy drop, BAD)应用于后门攻击中[43]。该指标表示分别使用污染前后数据训练模型, 两模型在无污染的测试数据上精确度的差距。该指标用于衡量注入攻击的隐蔽性, 越小则证明后门攻击隐蔽性越好。

(4) 度平均值差异

度平均值差异(Average degree difference, ADD)表示攻击前后测试样本节点度的平均值之差。该指标应用在后门攻击中[43], 用于衡量注入攻击的隐蔽性, 其值越小证明后门攻击隐蔽性越好。

(5) 节点选择成功率

节点选择成功率(Success rate with node selection, SRNS)表示将扰动添加到多跳邻居中, 与随机添加扰动后, 目标模型的召回率之差[17]。该指标适用于多阶邻居的攻击场景, 用于衡量攻击效果, 其值越低表示多阶扰动的效果越好。

(6) 分类准确率变化

分类准确率变化(Change in classification accuracy, CCA)表示攻击前后目标模型分类准确率之差[48], 用于衡量针对分类任务的攻击效果, 变化率越大则证明攻击效果越好。

(7) 损失变化

损失变化(Loss change)表示攻击后目标模型的损失提升程度。变化程越大则攻击效果越好[49]。

(8) 相似度分数

相似度分数(Similarity score, SS)表示节点向量之间的距离, 该指标通常用于衡量对节点嵌入模型的攻击效果。在攻击中, 两正(负)例间的相似度下降, 或正负例间的相似度上升都能体现攻击的有效性。Sun等[12]对基于图嵌入的链路预测模型进行攻击, 改变目标节点周围的拓扑结构, 提升了正例、负例节点间相似度导致预测出错。

(9) 攻击时间

攻击时间(Attack time, AT)一般用来衡量算法复杂度。文献[47,50]对传统的攻击方法进行改进, 从攻击时间上证明新方法的优势。

(10) 模块化度量Q

模块化度量Q[15](Modularity Q)表示社区内连边eii(端点位于同一社区)与跨社区连边(端点位于不同社区)数量平方2a的差。在针对社区检测模型的攻击中, 模块度Q越小, 表示模型划分的结构越不稳定, 则攻击效果越好。计算攻击表示为[15]:

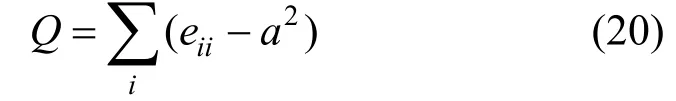
(11) 单个对抗样本生成时间

单个对抗样本生成时间(Generating time in seconds per-sample, GTSP)用来衡量生成对抗样本的效率。恶意代码检测模型的攻击场景中, 单个样本生成时间越短, 则固定时间内生成的对抗样本越多, 说明攻击者的攻击能力越强[18]。

(12) 修改特征平均数量

修改特征平均数量(Average number of features inserted, ANFI)表示在攻击成功的情况下, 修改节点特征的数量的平均值。其值越小则攻击者花费的代价越小[18], 则攻击模型设计越合理。

(13)M1和M2

M1和M2[51]都表示节点被分类到其他社区中的概率。在规避社区检测模型的场景中, 两项指标越大则目标节点隐藏程度越高, 攻击效果越好。计算表达式为[51]:

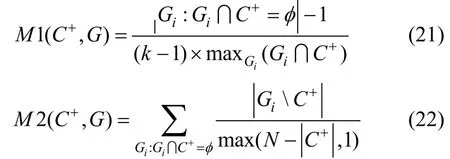
其中C+表示目标社区的节点集合,iG表示其他类别的社区。

(14)Hit@10

Hit@10表示推荐列表前10位中出现目标商品的用户数量与全部用户数量之比。Fang等[52]攻击Top-K类型的推荐系统, 通过在普通用户周围注入恶意用户, 大大提升了目标商品的Hit@10。Zhang等[41]研究了基于知识图谱嵌入的实体预测攻击, 对于每个训练三元组(h,r,t), 使用其他实体作为候选项来替换h或t。预测阶段Hit@10值越小则嵌入效果越差, 攻击越成功。计算表达式为:

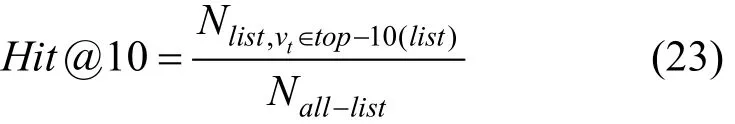
其中Nlist,vt∈top-10(list)表示推荐列表包含目标节点vt的用户数量,Nall-list表示所有用户数量。所有指标及文献见表 1所示。

表1 图深度学习攻击模型评价指标 Table 1 The evaluation of deep learning based graph

4 常用数据集介绍

根据图深度学习模型任务, 可将常用数据集划分至分类任务, 链路预测任务, 其他任务三大类任务中。分类任务旨在利用模型得到节点或图的标签, 因此分类任务的数据集重点关注节点或子图的类别数量的相关信息; 链路预测任务旨在求解图中两节点之间存在连边的概率, 数据集的重点关注节点和连边的数量; 其他任务中包括推荐任务、社区检测、顶点提名等, 数据集的重要特征视不同任务有所区别。从现有的工作来看, 分类任务和链路预测任务是当前的研究热点。

数据集中, Cora[57]、Citeseer[57]、Pol.Blogs[58]被广泛应用于分类任务的评估中, 同时一些链路预测任务也使用了Cora和Citeseer数据集。Reddit[59]数据集包含大量的用户和评论, 且用户的类别标签足够丰富, 可应用于节点/图分类任务, 文献[60]还将其应用于舆情控制问题中。BA模型生成的无标度网络数据被用于图分类任务[37]和链路预测问题[50]中。Twitter和Facebook数据集是社交网络中常用的数据集, 可用于分类问题和链路预测任务中。KarateClub[61]、Dolphin[62]、Football Network[63]、Email-Eucore Network[64]是典型的社区检测任务数据集。数据集对应任务及文章见表 2所示。

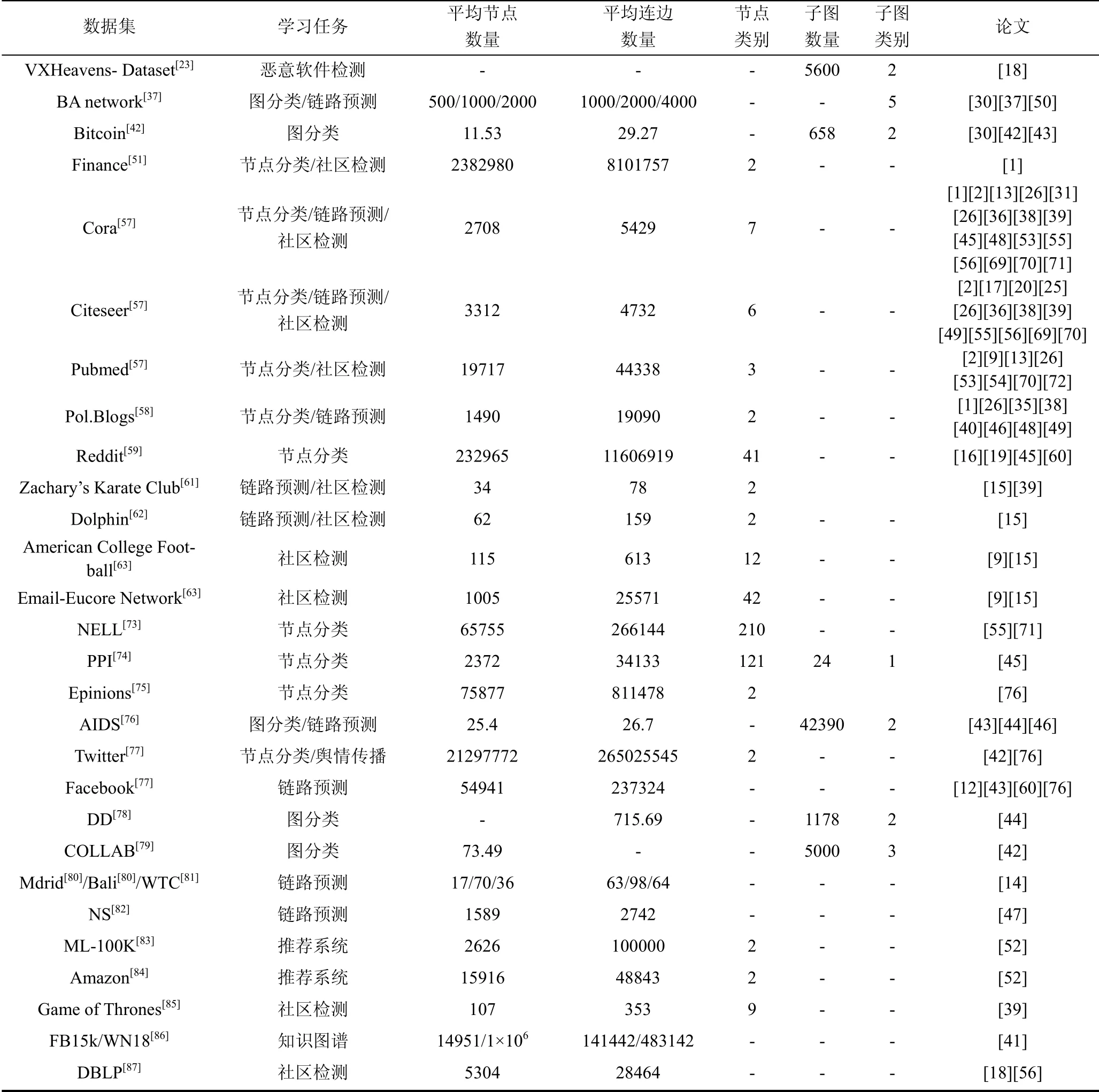
表2 图深度学习模型常用数据集 Table 2 Dataset of deep learning based graph

5 现有挑战与未来展望

5.1 现有挑战

现有的图深度学习攻击问题研究中, 攻击者仍然面临一些难以解决的难题。

1) 扰动的隐蔽性及评价标准

当前攻击研究的挑战之一是确保扰动具备足够的隐蔽性。在图像领域中, 攻击者通过限定像素值变化的范围来保证对抗的隐蔽性。而对于离散的图结构数据, 现有工作通过约束扰动或采用预定义分布的方法[2]解决攻击的隐蔽性问题。约束扰动是指, 限制扰动连边/特征的数量。直观来说, 当添加扰动的数量规模足够小, 则就可以认为扰动足够隐蔽。预定义分布是指攻击者添加扰动后不破坏原始数据的统计分布特征(如幂律分布等)。但两种方案仍存在一定限制: 约束扰动多采用人为定义的方法, 缺乏一定的数据支撑; 预定义分布在理论上有效果, 但有研究证明真实的数据服从不同的分布特征[65], 人为假设的分布规律同实际的图数据分布特征可能不同。同时, 由于扰动类型的不同, 攻击者在保证隐蔽性时, 攻击代价的衡量标准不相同, 也是当前面临的挑战。

2) 扰动添加的离散优化问题

在图深度学习模型的攻击研究中, 受限于扰动的离散性, 如何合理表示扰动对梯度的影响, 以及利用梯度寻优的过程存在挑战。扰动的离散性是指, 攻击者只能选择添加/删除连边或节点特征。虽然传统的对抗攻击方法FGSM[66]和C&W[67]的方法在连续空间域(如图像、文本)上有比较好的表现, 但不能直接应用在离散优化问题的求解上。此外, 即使定义出了梯度表示, 在大规模的图数据中该问题往往是NP难的。因此, 如何转化离散优化问题, 简化计算也是目前研究的面临的困难之一。

3) 黑盒/灰盒攻击研究较少

真实场景中的攻击多是黑盒和灰盒攻击。由于黑盒/灰盒攻击在寻找最优攻击节点/连边的问题上存在一定限制, 目前多数研究仍假设攻击者掌握白盒知识。黑盒攻击的研究还不够深入, 其建模与求解过程仍存在相当的挑战。

4) 扰动添加后的再训练问题

投毒攻击中, 如何解决模型重训练代价过大是当前研究者们需要重点考虑的问题之一。逃逸攻击不需要对原始模型做出修改, 因此假设模型是静态的。但投毒攻击在模型训练过程中发生, 对抗样本注入后可能会对目标模型训练结果产生影响, 攻击者必须对模型进行重新训练[68]。若图的规模较大或目标模型的训练过程较复杂, 则重训练会消耗巨大的计算资源, 增加攻击者的攻击成本。因此, 如何摆脱重训练的带来的问题, 是攻击者们需要解决的难题。

5.2 未来展望

未来工作中, 我们可以将图深度学习与以下问题或方法进行结合, 进一步解决不同应用场景下的特殊问题。主要包括:

1) 多种约束共同作用

未来工作中, 攻击者应当考虑结合离散域和原始图的分布特征制定攻击模型的约束条件。目前大多数攻击者通过改变目标节点的拓扑结构来进行攻击, 且仅从离散域约束来保证隐蔽性。文献[10]中提出, 若不考虑添加扰动后度分布的变化, 则会导致攻击隐蔽性的降低。则在扰动约束设计上, 不仅在离散域上限制修改连边(特征)的数量, 保证在不同规模的数据集上攻击的伸缩性; 同时, 在扰动添加后, 结合度、节点中心性、节点的特征分布等指标衡量攻击前后图数据的差异, 并以此作为额外的约束, 保证扰动后图数据能规避统计分析检测。两方面共同考虑使得攻击更加隐蔽。

2) 转化离散问题

图对抗中, 数据离散问题带来的挑战是, 扰动对目标模型的梯度影响很难定义。这直接影响扰动生成的计算难度。将离散问题进行合理转化能有效缓解计算难度, 如将离散的选择过程抽象为连续优化问题, 即利用连边选择概率替代原本的0/1选择; 也可利用近似梯度来替代离散域上的梯度变化; 或考虑绕过计算梯度, 采用基于启发式的方法来求解。

同时, 对于全图的离散优化问题, 已有研究证明可以利用局部图来表达全图的结构特征[88], 据此可将全图优化转化为局部图优化问题, 不仅能减少梯度计算的规模, 同时为未掌握全图信息的攻击者提供攻击机会。

3) 迁移攻击

目前, 多数研究假设攻击者掌握白盒知识, 在真实场景下假设很难成立。可通过建立替代模型, 并在替代模型上进行攻击, 将得到的对抗样本迁移到目标模型上。特别是在黑盒攻击场景下, 如何利用更少的知识构建更合理、更贴近原目标模型的替代模型, 是未来迁移攻击中需要不断优化的问题。

4) 结合增量学习

机器学习中, 增量学习模式解决了重训练的困境, 降低了模型更新对时间和空间的消耗。而在图深度学习攻击问题中, 投毒攻击在模型的训练过程中向训练数据中添加新扰动, 本质问题类似批量训练困境。未来工作中, 结合增量学习构建攻击模型, 学习新添加的数据对原始模型的影响, 减小计算代价是非常值得研究的问题。

5) 不同结构的图数据

现有的对抗工作大部分是针对静态图进行的, 相对于静态图表示, 动态图考虑了时序信息, 在诸如交通信息[89]、网络节点异常检测[90]等现实场景中表现更好。虽然动态图包含比静态图更多的信息, 但也因此增加了对抗的难度, CTDNE[91]、JODIE[92]等方法证明动态图上同样存在一定的安全隐患, 但由于现有的研究证明还不够充分, 因此未来的研究重点之一是在动态图上的对抗问题。

异构图比同构图更复杂, 其将实际系统抽象成图中不同类型的节点, 以对应真实场景中类型各异、彼此交互的组件。现有的异构图研究从2011年Sun等的研究[93]起发展至今, 已经在网络表示上有了大量成果[94-101]。异构图增加了图结构的复杂度, 也给攻击者带来更多的机会。基于同构图的传统手段在异构图上的有效性, 仍值得验证。同时, 复杂的图结构表明攻击具备更多的策略选择, 如何在规模更大的组合中挑选最有的扰动, 也是值得深入的问题。