基于可逆信息隐藏技术的认证方案的攻击与改进

王 泓, 黄方军,

1中山大学 计算机学院, 广东省信息安全技术重点实验室, 广州 中国 510006

2中国科学院信息工程研究所, 信息安全国家重点实验室, 北京 中国 100093

1 引言

近年来, 手机、便携式录音笔、以及摄像机等数字产品的日益普及, 为人们获取图像、音视频等多媒体文件提供了便利。人们可以非常方便地利用这些手持式设备拍照、录音或者摄像, 并将其上传到微信空间、个人微博等。同时, 随着计算机、网络、多媒体处理及传输技术等的飞速发展, 图像抓拍、音视频监控等设备也已遍布日常生活的每个角落。图像和音视频监控技术在社会治理、民生服务等领域得到了长足的发展。但同时我们也应看到, 随着计算机软件技术的迅速发展, 图像、音视频处理软件越来越多, 对图像、音视频等多媒体文件进行篡改也变得越来越容易。如何确保这些海量多媒体文件在存储和传输过程中的原始性和完整性是一个亟待解决的问题。信息隐藏是20世纪90年代发展起来的一门新的学科。其基本原理是利用人类感官系统对某些细节的不敏感性, 嵌入部分信息到原始载体而不引起观察者的怀疑。面对新形势下的海量多媒体文件, 利用信息隐藏技术来对其进行认证和保护具有非常重要的意义。

然而由于信息嵌入所具有的入侵特性, 信息隐藏在完成信息嵌入的同时会对原始载体引入改变。自20世纪90年代末期, 着眼于保护军事、医学和艺术等领域的高精度图像, 一门新学科即可逆信息隐藏(又叫可逆水印)受到了国内外学者广泛关注。不同于传统信息隐藏技术, 可逆信息隐藏技术可在提取所嵌入信息的同时无失真恢复原始载体。考虑到原始图像、音视频等文件可能会成为法庭上重要证据, 利用可逆信息隐藏技术对多媒体文件的原始性和完整性进行认证和保护, 同时确保原始载体可恢复, 在实际应用中具有重要意义。

当前应用于认证技术中的可逆信息隐藏主要采用三种方法: 无损压缩(Lossless compression)[2]、差值扩展(Difference expansion, DE)[3]和直方图平移(Histogram shifting, HS)[4]。无损压缩技术通常会在图像视觉质量上引入较大失真, 因此后两者近年来受到更多的关注。差值扩展[3]与直方图平移[4]类似, 都是对载体直方图(如原始直方图和差分直方图等)进行平移和扩展操作来进行信息的嵌入, 其中峰值点被扩展以嵌入秘密信息, 而非峰值点向两侧或某一侧平移以留出嵌入空间。由于平移操作主要用于预留空间, 无信息的嵌入, 通常被称作无效平移。一般图像越平滑, 图像中相邻像素的相关性越高, 产生的载体直方图的峰值越高, 对直方图进行扩展操作得到的嵌入容量越大, 同时无效平移而引入的图像失真越小。为了更好地利用相邻像素的相关性以提高嵌入容量并降低图像失真, 许多学者基于直方图平移与差值扩展技术提出一系列新的基于预测误差直方图的方法, 包括基于一维预测误差直方图的方法[5-6]、基于多维预测误差直方图的方法[7-8]、基于像素值排序的方法[9-15]、基于多直方图的方法[16-17]、基于状态转移矩阵的方法[18-19]、基于非对称直方图[20-21]的方法等。上述方法通常以嵌入容量、视觉质量等作为衡量算法性能的主要指标, 在认证功能方面考虑较少。

由于对图像进行认证需要使认证信息尽可能地在图像中均匀分布, 具体来说是要分布到图像的每个子块, 甚至是每个像素中, 以便于检测出图像被篡改的位置, 因此要在完成认证的同时实现可逆是一项具有挑战性的工作。已有的一些基于信息隐藏的认证方法主要是对图像进行分块认证。如Lee和Suh利用差值扩展的方法对图像进行认证[22]。认证码的产生利用的是Holliman和Memon在文献[23]中采取的脆弱水印生成方式, 即首先通过图像自身的信息产生哈希序列, 将哈希序列与待嵌入的二值水印图像异或, 最后将异或后的信息嵌入到图像的每一个子块中。虽然在该方法中哈希序列的生成是由图像信息与密钥共同确定的, 但这种基于块独立的重复嵌入方法易受到伪造攻击[23]。

在文献[24]中, Lo和Hu提出一种新的基于可逆信息隐藏的认证方法。该方法首先将图像分成N个子块, 并在每个子块中生成预测误差直方图, 然后对预测误差直方图进行扩展平移操作从而将N比特认证信息分别嵌入到N个子块中。但考虑到部分子块的嵌入容量可能为0, 因此对这部分嵌入容量为0的子块难以进行有效认证。Nguyen等人[25]及Yin等人[26]分别通过对图像进行小波变换和引入希尔伯特曲线, 对Lo和Hu的方法进行改进, 从而提高了嵌入容量与认证精度。但二者的方法在安全性上仍存在一定的漏洞, 如可对图像进行以下篡改, 对块中的所有像素值同时加上一个常数(常数攻击)[1], 确保预测误差直方图保持不变, 由于上述的认证方法是通过对预测误差直方图扩展平移来嵌入认证信息的, 因此常数攻击后认证方提取的认证信息与嵌入方嵌入的一致, 篡改无法被检测。

为了进一步提高安全性, Hong等人[1]提出了基于IPVO[11]和LSB替换的认证方法。在该方法中, Hong等人根据嵌入容量将子块分为两类, 即嵌入容量大于0的子块和嵌入容量等于0的子块。该认证方法不仅能对嵌入容量大于0的子块用IPVO的方法进行认证, 且巧妙地利用了LSB替换对嵌入容量为0的子块进行认证, 有效提高了认证精度。同时对于常数攻击, 该方法也能有效地进行检测。

该方案提出后, 受到国内外学者的较多关注[27-29]。本文针对Hong等人提出的方法[1]进行深入研究, 指出该方案中由于攻击方能准确获知认证图像中参与了认证码生成和提取的部分像素, 在安全性方面还存在明显缺陷。针对这些缺陷, 本文提出了一种针对性的攻击方案, 即选择对子块中不参与认证码生成且不影响认证信息提取的像素进行篡改, 从而使得Hong等人认证方案无法准确检测一些针对性且有意义的篡改。为了提高算法的安全性, 本文还提出了相应的改进方案。理论分析和实验结果验证了本文提出的攻击和改进方案的有效性。

本文的具体安排如下: 第二节简单介绍了IPVO方法及Hong等人提出的基于可逆信息隐藏的认证方法, 第三节给出了本文所提出的攻击和改进方案, 并在第四节给出了我们所提出的攻击与改进方案的具体实验结果, 最后在第五节我们对本文进行了总结。

2 相关工作

Hong等人提出的基于可逆信息隐藏的认证方法主要基于IPVO方法来实现, 这一部分我们将首先介绍IPVO方法, 再对Hong等人提出的认证方法进行分析。

2.1 IPVO方法[11]

IPVO是对Li等人提出的PVO方法[9]的改进, 两者均采用分块嵌入方案。不失一般性, 设图像中任意子块像素为。首先对子块中的像素按像素值的大小升序排序, 得到排序后的像素值序列为, 其中下标σi表示xσi在初始序列中的位置。排序方式为稳定排序, 即当xi=xj且i＜j时, 有σi＜σj。PVO方法直接采用最大像素值减第二大像素值, 最小像素值减第二小像素值来得到预测误差值, 并进而构造预测误差直方图。通过改变每个子块内的最大和最小像素以实现对预测误差直方图的扩展和平移操作, 进而完成信息的嵌入。PVO方法中, 一般选择对预测误差值1和–1进行扩展, 对小于–1和大于1的预测误差值分别向左右两边平移以腾出空间。

为了进一步提高嵌入容量, IPVO在计算预测误差值时考虑了像素值的位置信息, 从而可以利用预测误差值0进行扩展嵌入。预测误差值的计算如公式(1)和(2)所示

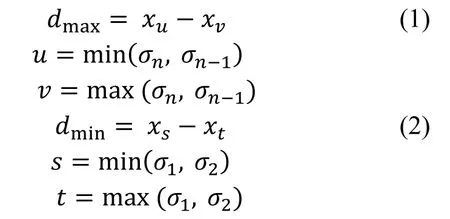
在上述公式中, 当σn＜σn-1时, u=σn, v=σn-1, 由排序的方式可知此时有dmax＞0; 当σn＞σn-1时, u=σn-1, v=σn, 根据排序的方式可知此时有dmax≤0。对于dmin同理。

分别构造关于dmax与dmin的预测误差直方图, 具体信息嵌入如公式(3)和(4)所示

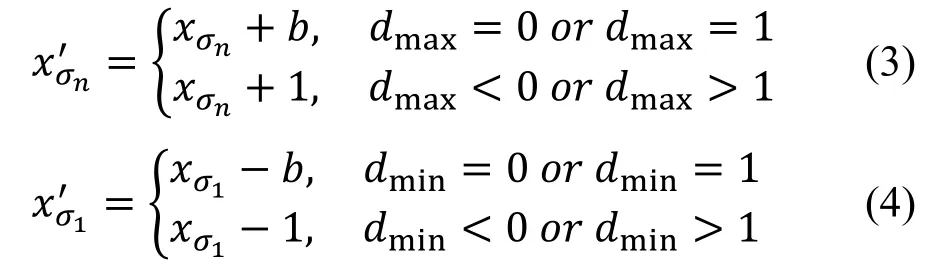
在公式(3)和(4)中,b表示要嵌入的认证信息比特。由公式(3)可见: 当嵌入信息为b= 1时, 该子块内的最大像素值xσn加1, 此时预测误差值如为0则扩展为 –1, 如为1则扩展为2; 当嵌入信息为b= 0时, 该子块内的最大像素值保持不变, 此时预测误差值无论是0还是1均保持不变; 当预测误差值小于0或大于1时, 对预测误差直方图进行平移操作, 即对最大像素值加1, 使得小于0和大于1的预测误差值分别向左右两边平移。公式(4)对该子块内最小像素值的操作同理可得。由嵌入规则可知, 嵌入信息后任意子块中最大像素值和最小像素值仍为该子块中的最大和最小值。

对于提取方, 同样对子块中的像素按像素值大小升序排序, 排序后用同样的方法计算预测误差, 根据预测误差值提取信息并恢复图像。在提取公式(5)和(6)中, b为提取的认证信息比特。由公式(5)和(6)可知: 当预测误差值为0或1时, 提取认证信息比特b=0; 当预测误差值为-1或2时, 提取认证信息比特b=1。

原始载体图像按照公式(7)和(8)进行恢复。

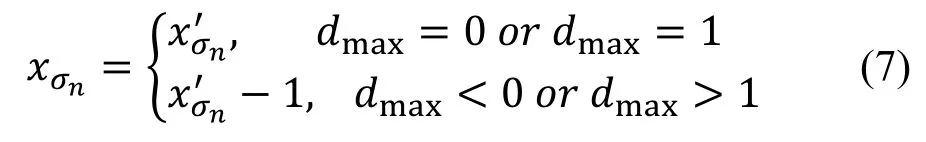
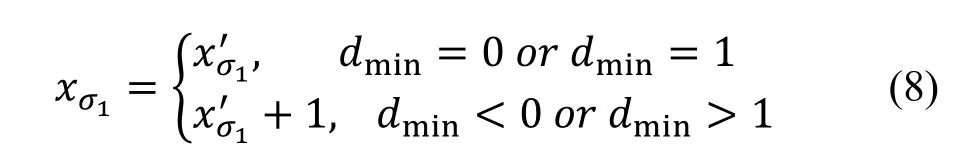
2.2 Hong等的的认证方法[1]

在Hong等人的方法中, 首先对图像分块, 并按嵌入容量将块分成可嵌入块和非可嵌入块, 然后针对不同类别的块分别用IPVO和LSB替换方式进行认证。具体的认证方案如下。

2.2.1 块分类

在Hong等人的基于可逆信息隐藏的认证方法中, 首先对原始载体图像进行4×4不重叠分块, 再将所得的每一个4×4图像块进一步划分成4个2×2的子块, 具体划分方式如图1所示。为了便于说明, 我们将4×4的图像块称为嵌入块, 将2×2的子块称为嵌入单元, 根据嵌入块的嵌入容量又将其分为可嵌入块(即E块)和非可嵌入块(即U块), 其中E和U分别代表Embeddable和Unembeddable, 其具体分类方案如下:

图1 块Bi的划分 Figure 1 The partition of block Bi

1) 对每个2×2嵌入单元中的像素按像素值大小升序排序;

2) 计算2×2嵌入单元中的预测误差值dmax与dmin, 根据其为0和1的数量计算该嵌入单元的嵌入容量, 由IPVO算法可知每个2×2嵌入单元的嵌入容量最多为2;

3) 将4个2×2嵌入单元的嵌入容量相加得到整个嵌入块的嵌入容量, 整个嵌入块的嵌入容量最多为8, 最少为0;

4) 当整个嵌入块的嵌入容量为0时将其分类为U块, 否则分类为E块。

2.2.2 U块认证

首先对U块进行预处理, 具体如下: 1) 对所有2×2嵌入单元所属的预测误差直方图进行平移操作, 如当原始嵌入单元中得到的预测误差值为–1或2时, 平移后分别为–2或3; 2) 在平移后的嵌入块中根据密钥key任意选择一个嵌入单元, 将该嵌入单元中的最小像素值与最大像素值进一步向左右两边各平移两个单位, 即进行减2和加2的操作。上述预处理主要用于确保在该嵌入块的任意2×2嵌入单元中, 所得的预测误差值均一直大于2或小于–1, 从而使认证方在提取信息过程中不至于与E块混淆。

对预处理后U块的认证方案如下: 1) 根据当前嵌入块的所有像素7个高位平面的值及当前嵌入块的位置信息生成1比特的认证码; 2) 用认证码替换根据秘钥key选定的2×2嵌入单元中左上角像素的LSB位, 对该嵌入块进行认证, 并将被替换的LSB顺次保存在数组中。

2.2.3 E块认证

对E块进行认证无需进行预处理, 记当前E块的嵌入容量为α。对E块认证过程具体如下: 1) 对每个2×2嵌入单元中的像素按其像素值大小升序排序, 分别提取每个嵌入单元中居中的2个像素, 共得到8个像素; 2) 根据这8个像素的像素值及当前嵌入块的位置信息生成α-1比特的认证码, 记当前的认证码为A(注: 当嵌入容量α=1时, 直接生成1比特认证码即可); 3) 从2.2.2节中得到的S数组中顺次提取1比特, 并将其和A进行拼接, 得到的α比特记为即= A | si(注: 当α=1时, 认证码不与si进行拼接, 即=A); 4) 将α比特的用IPVO方法嵌入到当前嵌入块中。

3 攻击与改进方案

根据前文介绍可知, Hong等人的方法中, 由于分块信息是公开的, 攻击方无需其他信息即可准确计算出每一个嵌入块的嵌入容量, 再根据嵌入容量可将其准确分类为U块或E块。同时对于嵌入容量不为0的E块, 攻击方也可以根据IPVO的嵌入和提取规则, 准确得到嵌入方具体通过改变哪些像素值嵌入信息。根据上述分析, 我们提出如下的攻击及改进方案。

3.1 攻击方案

攻击方按照已公开的分块信息, 对图像进行分块并将嵌入块划分成4个嵌入单元。计算出嵌入块的嵌入容量后进行块分类, 若为E块则按照一定规则修改嵌入单元的最大或最小像素, 若为U块则按照一定规则修改嵌入单元中的非左上角像素。攻击方案的流程如图2所示。

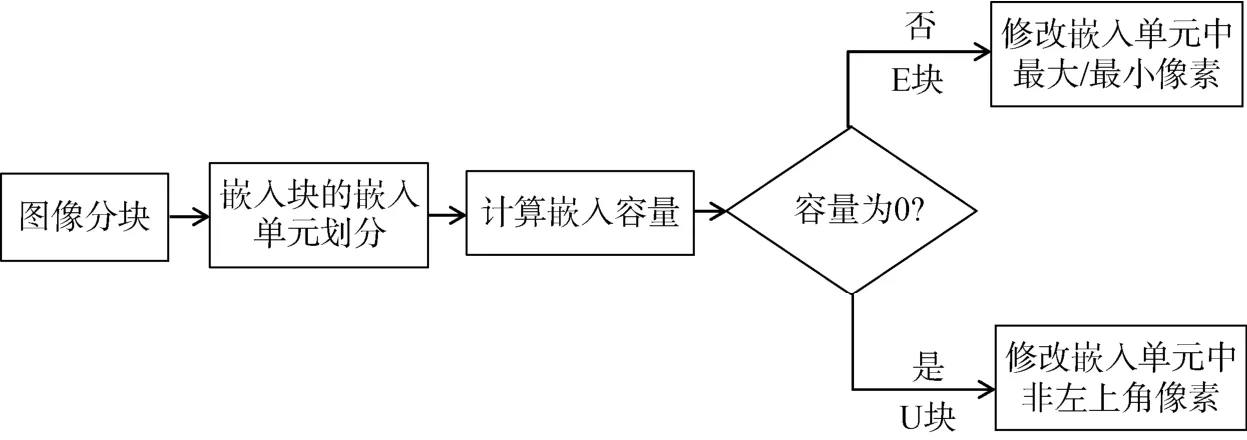
图2 攻击方案流程图 Figure 2 The flowchart of the attack

3.1.1 E块攻击

认证方在对E块进行认证时, 首先提取出所嵌入的认证信息, 然后根据原嵌入方所采取的方式重新生成认证信息, 将提取出的认证信息与重新生成 的认证信息进行比对, 若二者一致, 则表明该E块没有被篡改, 反之则表明该E块已被篡改。因此对E块攻击后要达到的主要目标包括: 1) E块篡改前后认证方提取的认证码保持不变; 2) E块的篡改不影响认证信息的生成, 即篡改前后运用原嵌入方所采取的方式生成的认证信息保持不变。

根据公式(5)和(6)IPVO算法的提取规则, 只有当预测误差值属于{–1, 0, 1, 2}时, 认证方才可提取出对应的认证信息, 因此要保证E块篡改前后认证方提取的认证码保持不变, 只需在篡改前后确保与预测误差值{–1, 0, 1, 2}相关的所有像素值保持不变即可。另一方面, 由于E块认证码的生成只与E块中每个2×2嵌入单元中的两个中间像素相关。因此, 要使得对E块的篡改不影响认证信息的生成, 只需确保每个2×2嵌入单元的中间两个像素保持不变即可。

由上述的分析可知, 篡改方可对不参与认证码生成且不影响认证信息提取的像素进行篡改。具体到每一个2×2嵌入单元, 只要在该嵌入单元中计算得到的预测误差值不属于{-1, 0, 1, 2}, 则可对最大或最小像素值进行修改。具体篡改方案如下:

1) 对E块中2×2嵌入单元的像素按其值的大小升序排序, 由公式(1)与(2)分别计算出预测误差值dmax与dmin;

2) 当dmax∉-1,0,1,2时, 将2×2嵌入单元最大像素值增加为不大于255的任意值;

3) 当dmin∉-1,0,1,2时, 将2×2嵌入单元最小像素值减小为不小于0的任意值。

经过篡改, E块中嵌入单元的最大和最小像素值仍为嵌入单元中最大和最小值, 不会对E块的嵌入容量产生影响, 也就不会影响认证方对嵌入块的分类。而 篡 改 仅 发 生 在dmax∉-1,0,1,2与dmin∉-1,0,1,2的那些嵌入单元的最大和最小像素值上, 对认证信息的提取与重新生成均不会产生影响。

3.1.2 U块攻击

认证方在对U块进行认证时, 首先提取出所嵌入的认证信息, 然后根据原嵌入方所采取的方式重新生成认证信息, 将提取出的认证信息与重新生成的认证信息进行比对, 若两者一致, 则表明该U块没有被篡改, 反之则表明该U块已被篡改。

根据上文介绍, Hong等人的方法中, 对于U块嵌入方仅利用预处理后图像的当前嵌入块所有像素的7个高位平面来生成认证码, 因此只需保证当前嵌入块所有像素的7个高位平面不变, 即可确保篡改前后生成的认证码保持不变。

此外, 由该认证方法可知, 嵌入方用密钥key随机选择嵌入块中任意一个2×2嵌入单元, 并用1比特认证码替换该2×2嵌入单元左上角像素的LSB。虽然篡改方无法准确得知嵌入方所选中的2×2嵌入单元, 但篡改方只需保证每个2×2嵌入单元的左上角像素保持不变即可, 从而可确保篡改前后从载体图像中提取的认证码保持不变。

根据上述分析, 在对U块进行攻击时, 首先要确保每个2×2嵌入单元的左上角像素保持不变。另外, 由于U块所有像素的高7位均用于认证码的生成, 所以对U块的攻击只考虑对每个2×2嵌入单元的非左上角像素LSB位进行翻转攻击。但根据2.2.3节可知, U块是非可嵌入块, 在其每一个2×2嵌入单元中均有dmax∉-1,0,1,2与dmin∉-1,0,1,2成立, 因此若随机对非左上角像素的LSB位进行翻转攻击, 有可能导致dmax∈-1,0,1,2或dmin∈-1,0,1,2, 从而进一步导致认证方无法准确定位U块和E块。因此对U块的篡改可采取如下方式:

1) 计算每个2×2嵌入单元的预测误差值dmax与dmin;

2)在确保dmax∉-1,0,1,2和dmin∉-1,0,1,2的情况下, 对每一个2×2嵌入单元的非左上角像素LSB位进行随机翻转。

3.2 改进算法

由于对E块像素值的修改幅度更大, 对像素的篡改效果更加明显, 第4节中将给出实验对此进行说明, 因此对于E块考虑更加安全的认证码生成策略。

根据上文提出的攻击方案可知, 由于在Hong等人的认证方法中可嵌入块E块的每个2×2嵌入单元中的最大和最小像素值均不参与认证码的生成, 因此可对其进行较大幅度的修改。为了提高认证算法的安全性, 可以考虑将E块中的所有像素均引入到认证码的生成过程。具体实施过程中, 可以考虑在嵌入认证信息前, 根据该E块的所有16个像素及其位置信息来生成认证码, 并将其按Hong等人的方法嵌入到相关嵌入块中。不同之处在于, 认证方在进行认证时, 先按公式(7)和(8)对原始载体进行恢复, 并根据恢复后得到的嵌入块重新生成认证码, 然后将其与提取的认证信息进行比对以确定当前可嵌入块是否被篡改。

图3说明了改进算法与Hong等人的认证算法对E块认证时的区别, 图3(a)和(b)中的红色区域分别是Hong等人的算法与改进算法中参与认证码生成的像素, 与Hong等人的认证算法相比, 改进算法在生成认证码时考虑了嵌入单元中的最大和最小像素值。

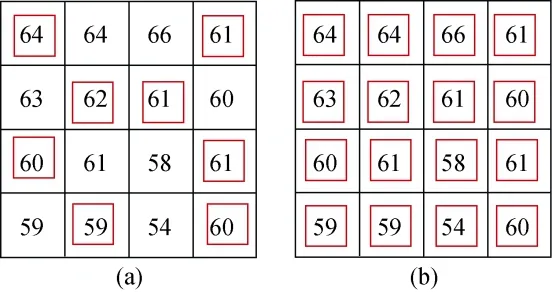
图3 Hong等人算法(a)与改进算法(b)参与认证码生成的像素对比 Figure 3 The difference of the pixels participating in the generation of the authentication code between the Hong’s algorithm (a) and the improved algorithm (b)

此外, 根据Hong等人的算法可知, 分块信息是公开的, 因此攻击方能够根据嵌入块的划分方案, 计算得到嵌入块的嵌入容量, 进而对其进行准确分类。无论对于E块还是U块, 攻击方能够准确得知嵌入方针对每个2×2嵌入单元的预测误差直方图所采取的扩展或平移等操作。为了避免攻击方获知嵌入块的划分方案, 可在划分嵌入单元之前对嵌入块进行Arnold置乱, 再将置乱后的嵌入块进一步划分成4个2×2嵌入单元。在Arnold置乱的过程中需要3个正整数参数, 分别记为a,b,n, 其中a,b为映射矩阵的参数,n为迭代次数, 三个参数数值过大时易导致计算速度降低, 本文将a,b,n的大小均控制在[1, 256]之间, 则每个参数均用8比特即可存储。用密钥key对置乱参数进行加密, 将其以差值扩展的方式嵌入已嵌入认证信息的图像中。认证方同样以差值扩展的方式提取并解密得到置乱参数。

至此, 改进算法可总结如下:

1) 对原始载体图像进行4×4不重叠分块, 对每个4×4嵌入块进行Arnold置乱, 将置乱后的嵌入块按图1的方式进一步划分成4个2×2嵌入单元, 并将置乱参数存于数组S中;

2) 同样根据嵌入块的嵌入容量将其分类为U块和E块;

3) 对于U块, 按与Hong等人的方法相同的方式进行认证码的生成与嵌入;

4) 对于E块, 根据所有像素的像素值及当前嵌入块的位置信息生成认证码, 认证码的长度与嵌入容量α的对应关系与Hong等人方法中的相同, 然后同样用IPVO方法将α比特信息嵌入到嵌入块中。

改进算法与Hong等人的方法相比, 将可嵌入块E块中更多的像素引入了认证码的生成过程, 同时在对所有嵌入块划分嵌入单元之前增加了对嵌入块置乱的过程。由于置乱后嵌入块中相邻像素的相关性减弱, 一定程度上会使嵌入容量降低, 但基本不会对认证产生影响, 第4节中将会有相关实验结果对此进行进一步的说明。

4 实验结果

实验过程中我们主要针对图4中的6副512×512的灰度图像进行了测试, 具体包括攻击实验和改进算法实验两个部分。攻击实验部分我们主 要通过篡改像素个数及篡改前后图像之间的峰值信噪比(Peak signal-to-noise rate, PSNR)来对篡改效果进行说明。在改进算法实验部分, 我们从PSNR、随机攻击的检测率及用本文攻击方法针对性攻击后改进算法的检测效果三个方面来对本文提出的改进算法的效果进行说明。

图4 实验图像 (a) Tank (b) Splash (c) House (d) Lena (e) Pepper (f) Plane Figure 4 Experimental images (a) Tank (b) Splash (c) House (d) Lena (e) Pepper (f) Plane

4.1 攻击实验

攻击实验包括对E块和对U块的攻击两个方面, 我们运用前文所给出的攻击方案分别进行了实验, 具体如下。

4.1.1 E块攻击实验

首先用Hong等人的方法对图4所示6幅灰度图像进行认证信息的嵌入, 再用本文提出的攻击方法对图像中的E块进行攻击。为使篡改效果更加显著, 当2×2嵌入单元中的最大像素值可修改时, 将其均修改为255; 当2×2嵌入单元中的最小像素值可修改时, 将其均修改为0(注: 根据上文的E块攻击策略, 上述篡改不影响认证方认证信息的生成和提取, 即认证方无法确认该图像已被篡改)。具体实验结果如表1所示。

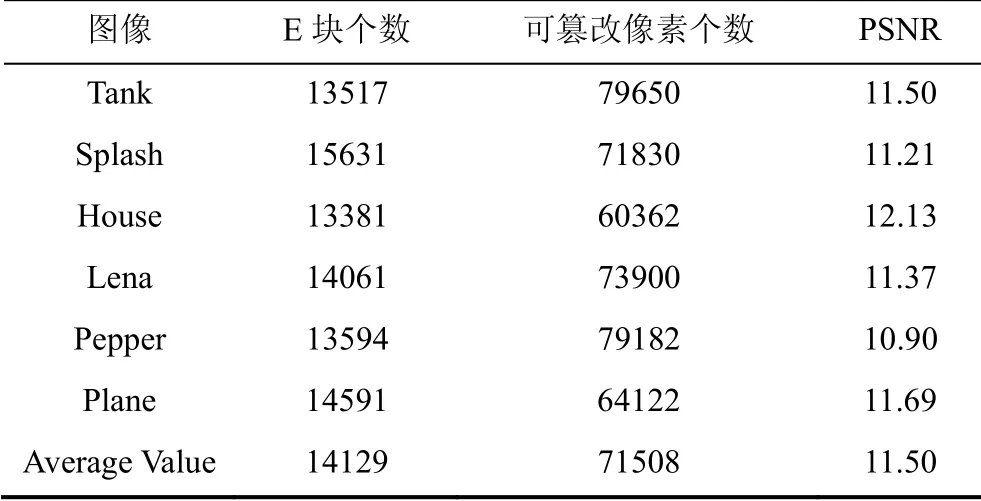
表1 E块篡改实验结果 Table 1 Results of tampering E blocks

表1中的第一列为本文实验中所采用的所有图像, 第二列是每幅图像中E块的个数(注: 整幅图像所包含4×4分块的个数为16384), 第三列是图像可篡改像素个数, 第四列是篡改前和篡改后图像之间的PSNR值。由表1可见, 在所有6幅图像中E块比例均较高(E块个数最少的House图像, 其E块比例高于81%), 可被篡改的像素个数也相对较多, 篡改后的图像质量有了大幅度的下降, 表中最小的PSNR值为10.90, 最大的PSNR值小于12.20, 平均值仅为11.50。说明对E块的攻击可以取得非常显著的篡改效果。

图5给出了对运用Hong等人方法嵌入认证信息后Lena图像中所有的E块进行针对性攻击后的结果, 可以看到被篡改后的图像会呈现类似于添加了椒盐噪声的效果, 这是因为篡改时部分像素值被修改为255, 部分像素值被修改为0, 且可篡改的像素在图像中分布相对均匀。实验过程中我们还对图5用Hong等人的方法进行认证, 经过验证, 从图5中提取的认证信息与按照Hong等人方法生成的认证信息完全匹配, 即Hong等人所提出的认证方法无法检测出图5中的篡改。

图5 对所有E块攻击后的Lena图像 Figure 5 Lena image after attacking all E blocks

考虑到图5中的篡改类似于添加随机噪声, 在图6中我们给出了有意义篡改后的图像, 即对使用Hong等人方法嵌入认证信息后的图像中部分E块, 运用本文E块攻击方案进行篡改后, 使得图像中出现图6(c)所示的中国银行图标。图6(a)是对嵌入认证信息后的Lena图像在其左上角进行局部篡改后的图像, 篡改后图像左上角处显现图6(c)所示的中国银行的图标。图6(b)为对嵌入认证信息后的Lena图像在多个位置进行有意义篡改后的图像, 篡改后图像 中的左上角处, 镜子处, 以及人物肩膀下方均出现图6(c) 所示中国银行图标。经过验证, Hong等人的认证方法无法检测出图6(a)和(b)中的篡改。

图6 部分E块攻击后图像 (a)左上角篡改后Lena图像 (b)多个位置篡改后Lena图像(c)中国银行图标 Figure 6 The Lena image after tampering partial E blocks (a) The Lena image after tampering in the upper left corner (b) The Lena image after tampering in multiple locations (c) The bank of China icon

4.1.2 U块攻击实验

同样, 首先对图4中的6幅灰度图像用Hong等人的方法进行认证信息嵌入, 再用本文提出的攻击方法对U块进行攻击。具体实验结果如表2所示。

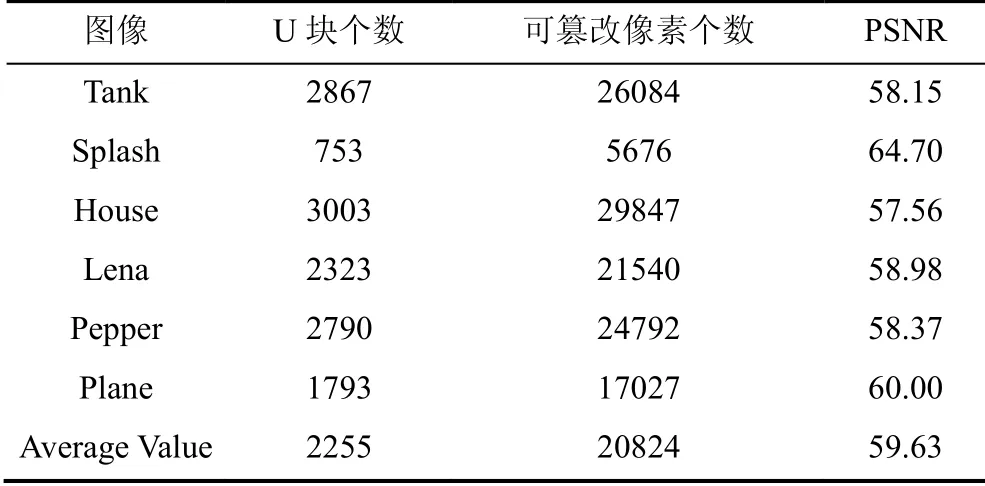
表2 U块篡改实验结果 Table 2 Results after tampering U blocks

表2第一列为本文实验中所采用的所有图像, 第二列是每幅图像中的U块个数(注: 整幅图像所包含4×4分块的个数为16384), 第三列是图像被篡改的像素个数, 第四列是篡改前和篡改后图像之间的PSNR值。由表2可见, 每幅图像U块的个数, 通常要远低于嵌入容量大于0的E块的个数, 分别在750～3800不等, 但平均篡改的像素个数仍有20000左右。虽然本文对U块的攻击仅针对像素的LSB位进行翻转(即对像素进行±1操作), 篡改前后图像之间的PSNR值平均约为59.63, 通常不能获得有意义的篡改图像, 但从图像真实性和完整性认证的角度而言, 本文所提出的U块攻击方案是有效的。

4.2 改进实验

根据第3.3节中的改进方案可知, 改进算法需要对4×4嵌入块(包括E块和U块)中的像素进行Arnold置乱。置乱操作通常会减小相邻像素之间的相关性, 导致后续得到的预测误差直方图峰值降低, 因此在认证信息嵌入过程中会增加无效平移的次数, 影响后续所得到的认证图像的视觉效果。但由于Hong等人算法中所选择的嵌入块一般为4×4大小, 因此置乱对图像像素之间相关性的影响相对较小。

表3分别给出了运用Hong等人算法嵌入认证信息后得到的图像, 以及运用本文所提出的改进方案嵌入认证信息后得到的图像与原始载体之间的PSNR值, 可以看到运用本文的改进算法后PSNR值的下降平均不超过0.3%。

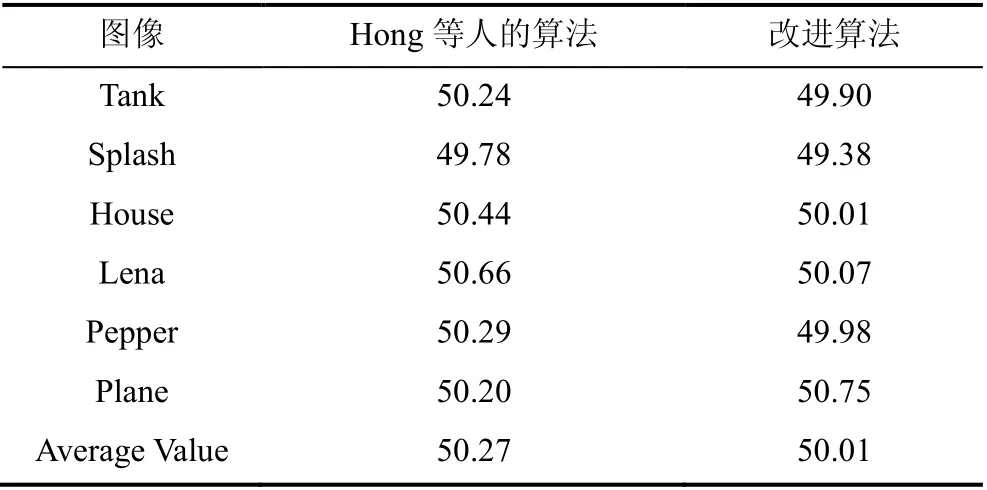
表3 PSNR对比 Table 3 Comparison of PSNR

表4对比了针对随机攻击的检测效果。随机攻击具体方式为: 随机选择图像中1%左右的嵌入块, 并将所选中块里面的每个像素的像素值随机修改为>0且<255的任意值。运用Hong等人的方法和本文改进算法对篡改后图像进行认证的正确检测率如表4所示, 其中正确检测率为正确检测出被篡改的嵌入块个数与真正被篡改的嵌入块个数的比值。由表4可知, 本文所提出的改进方案不影响Hong等人算法在普通随机攻击下的检测效果。注: 在Hong等人的方法中, 因为图像可嵌入块中可嵌入的认证码数量一般较少, 且为比特串, 根据篡改后图像生成的认证码有一定几率与从篡改后图像中提取的认证码正好相同, 因此通常正确检测率小于100%。

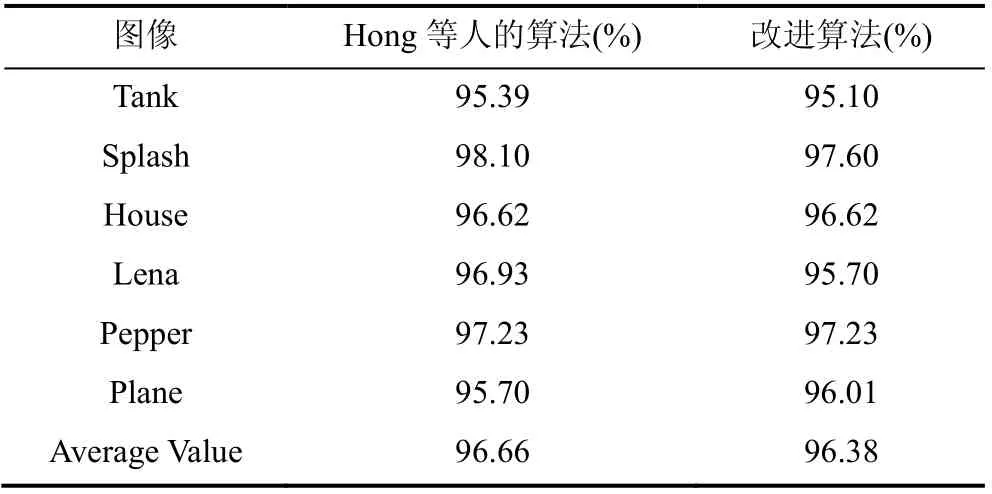
表4 随机攻击后正确检测率对比 Table 4 Comparison of correct detection rates of the random attack

图7给出了改进方案对本文所提出的针对性攻击的篡改检测效果。首先用改进算法在Lena图像中嵌入认证信息, 然后运用本文提出的攻击方法对图像中部分嵌入块进行针对性的篡改攻击, 使得篡改后图像中平滑程度较高的左上角处、镜子处和平滑程度较低的帽子与头发交界处出现如图6(c)的中国银行图标, 得到的篡改后的图像如图7(a)所示。对图7(a)运用改进方法进行篡改检测, 将检测到被篡改的嵌入块中所有像素值置为255, 得到检测结果如图7(b)所示。图7(b)中白色区域(像素值为255的区域)为运用本文改进方案检测并定位到的篡改区域, 可以看到改进算法能检测出针对性攻击并对篡改进行定位, 且对于不同平滑程度的区域均有成效。可见改进算法对本文提出的针对性攻击方案有较好的防御作用, 较大程度上提高了Hong等人算法的安全性。

图7 改进算法对针对性攻击的篡改检测结果(a)针对性攻击后Lena图像(b)篡改检测结果 Figure 7 The tampering detection results of targeted attacks for the improved algorithm (a) Lena image after the targeted attack (b) The tampering detection result

5 结语

基于可逆信息隐藏的认证技术能够在对图像的原始性和完整性进行认证和保护的基础上, 实现原始载体图像的无失真恢复。本文主要对Hong等人提出的一种新型认证方法进行深入研究, 主要贡献包括: 1) 对Hong等人所提出的认证方案的安全性进行了深入分析和研究, 指出了其在安全性方面存在的缺陷, 并提出了一种针对性的攻击策略; 2) 对Hong等人的方案进行了改进, 提高了Hong等人方案的安全性; 3) 本文所提出的攻击和改进策略对于所有基于PVO系列的认证方案具有一定的参考价值, 对后期设计更安全的认证方案具有较为重要的意义。