加筋高填方边坡稳定性影响因素分析
魏 浩,韩文喜,云海浪,马 捷,徐洪兵
(1.成都理工大学环境与土木工程学院,四川 成都 610059;2.成都理工大学地质灾害防治与地质环境保护国家重点实验室,四川 成都 610059;3.民航中南机场设计研究院(广州)有限公司,广东 广州 510000;4.中国建筑西南勘察设计院有限公司,四川 成都 610000)
边坡治理一直以来都是岩土工程界的热点问题,加筋土也是一种历史悠久的边坡支挡方式。国内外许多学者对加筋高填方边坡的稳定性做了一系列研究[1-5],但为了简化模型,研究对象往往比较特殊,如万年华[6]通过对不同坡高、坡度、填料的高陡加筋边坡进行离心模型试验,得出加筋使岩土边坡内部应力产生重分布,可以增加边坡稳定性系数,使潜在滑动面深度增加;赵偲聪[7]通过对降雨下的土质边坡进行离心模拟,发现短期暴雨下的边坡失稳为冲刷型破坏,长期小雨则会导致边坡发生牵引式破坏;Charles等[8]通过离心模型试验,研究了极蒸腾作用对降雨诱发边坡水文的影响。关于加筋土边坡数值模拟前人也做过许多研究[9-11],如邓方明等[12]运用有限元数值模拟手段分析了降雨入渗对台阶式加筋土挡墙稳定性的影响;Marián等[13]采用数值模拟手段,阐明2种计算MSE加筋墙体内部稳定性的方法,并与有限元数值模型进行比较。为进一步得到加筋高填方边坡的稳定性影响因素以及影响规律,以重庆巫山机场2号沟高填方边坡为研究对象,探究在同等加筋形式的情况下,不同坡度以及降雨条件对加筋土边坡的影响。
1 试验简介
取用现场填料用以制作模型填料,由于工程现场使用的填方土料颗粒过粗,为避免粒径效应影响,需对粒径进行缩尺,且缩尺后的最大粒径应为模型箱与模型结构物所允许[14-15]。本次试验采用的级配缩尺方法为梯形相似级配缩尺法[4],得到原型模拟填料(命名为A型填料),填料级配见表1。文献[16]中指出,理想的替代材料应该与原型材料有相同的强度和变形。结合实际工程与试验,最终选择耐碱玻璃纤维网作为模型格栅材料。由《土工离心模型试验规程》(DL/T 5102-1999)得模型层厚宜在2~8 cm之间,此时相当于格栅纵向间距成为原则上的6倍(2.2 cm),因此模型格栅抗拉强度也应扩大至原则上的6倍。根据厂家提供的信息,拟定3种模型格栅强度如下:A型7.86 MPa,对应原型抗拉强度为130 MPa;B型13.22 MPa,对应原型抗拉强度为200 MPa;C型18.54 MPa,对应原型抗拉强度为300 MPa。
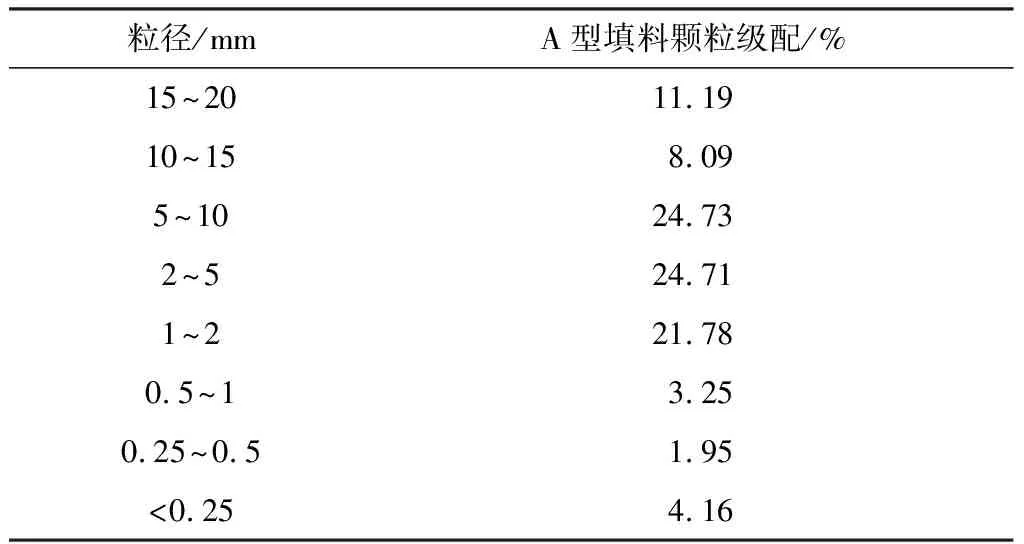
表1 填料级配Table 1 Filler gradation
此次试验原型的基岩为灰岩,风化程度低,其内部含有少量的岩溶并且经过充填处理。所以使用标准砖与水泥砂浆制作模型基岩,砂浆的强度参数保证试验过程中不发生显著变形及破坏且不透水即可,不需控制相似比。此次试验确定的基岩材料混合比为m水泥∶m粗砂=3∶1。
只要使离心模型的试验加速度加大到重力加速度的n倍,就可使模型达到与原型相同的应力水平状态[17-18]。离心模型试验比尺越小,同等条件下因元器件测量误差等导致的试验误差越小[19]。综合考虑后确定模型箱净尺寸为1.2 m(长)×1.0 m(宽)×0.8 m(高),按n=130比尺进行模型制作,130g进行试验。
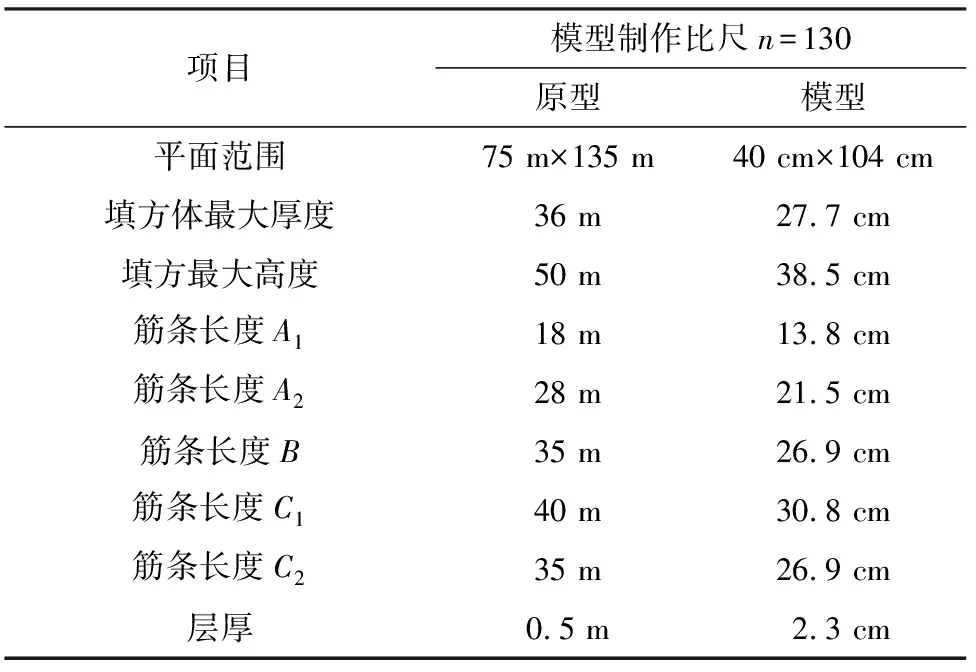
表2 原型与模型比尺对照Table 2 Comparison between prototype and the model
为模拟重庆巫山机场2号沟加筋土填方边坡的实际填筑过程,采用分级加载的方式。具体流程如下:
① 开机;
② 从0加载到30g,之后保持5.5 min(模拟时长0.5 d),模拟0~11.5 m高填方填筑过程;
③ 从30g加载到60g,之后保持5.5 min(模拟时长0.5 d),模拟11.5~23.1 m高填方填筑过程;
④ 从60g加载到90g,之后保持5.5 min(模拟时长0.5 d),模拟23.1~34.6 m高填方填筑过程;
⑤ 从90g加载到130g,之后保持5.5 min(模拟时长0.5 d),模拟34.6~50 m高填方填筑过程;
⑥ 保持130g,离心加速44 min(模拟时长4 d);
⑦ 停机。
在一定水压范围内,模拟降雨量随控制水压增加呈近线性增加趋势,则能通过控制水压来模拟预设的降雨强度。拟定降雨工况模拟上机方案如下:
① 开机,直接加载到130g;
② 增加水压至0.1 MPa(模拟降雨133.85 mm/d),保持11 min(模拟降雨时长1 d),之后停止加压5.5 min(模拟降雨间歇时长0.5 d);
③ 增加水压至0.2 MPa(模拟降雨168.93 mm/d),保持11 min(模拟降雨时长1 d),之后停止加压5.5 min(模拟降雨间歇时长0.5 d);
④ 增加水压至0.3 MPa(模拟降雨207.70 mm/d),保持11 min(模拟降雨时长1 d),之后停止加压5.5 min(模拟降雨间歇时长0.5 d);
⑤ 增加水压至0.4 MPa(模拟降雨244.62 mm/d),保持11 min(模拟降雨时长1 d),之后停止加压5.5 min(模拟降雨间歇时长0.5 d);
⑥ 停机。
2 离心模型试验结果分析
2.1 格栅应变分布情况
模型A-1的应变片全部布置在模型中轴面上。应变片传感器在中轴面上的分布情况如图1所示。

图1 模型A-1格栅应变片布置图Fig.1 Layout of strain gauge distribution of model A-1
由图1可知,应变片布置在模型格栅的四等分点。严格按设计的过程进行上机试验后,得到从底到顶的各层格栅在不同离心加速度下应变随距坡面距离的变化曲线(见图2)。

图2 模型A-1格栅在不同离心加速度下应变随距坡面距离的变化曲线Fig.2 Variation curve of strain changing with distance to slope of model A-1 under different centrifugal acceleration
由图2可以发现在离心加速度增加过程中部分应变片读数出现了负值,根据已有文献与本次试验具体现象推测可知,这种现象出现的原因是模型填料中的较粗颗粒在受力发生迁移的过程中对部分应变片产生了挤压作用,A-2模型也存在这种情况,其原因相同,不再赘述。
将模型A-1所测格栅应变最大处连接可得出该模型中潜在破裂面大致位置如图3所示。
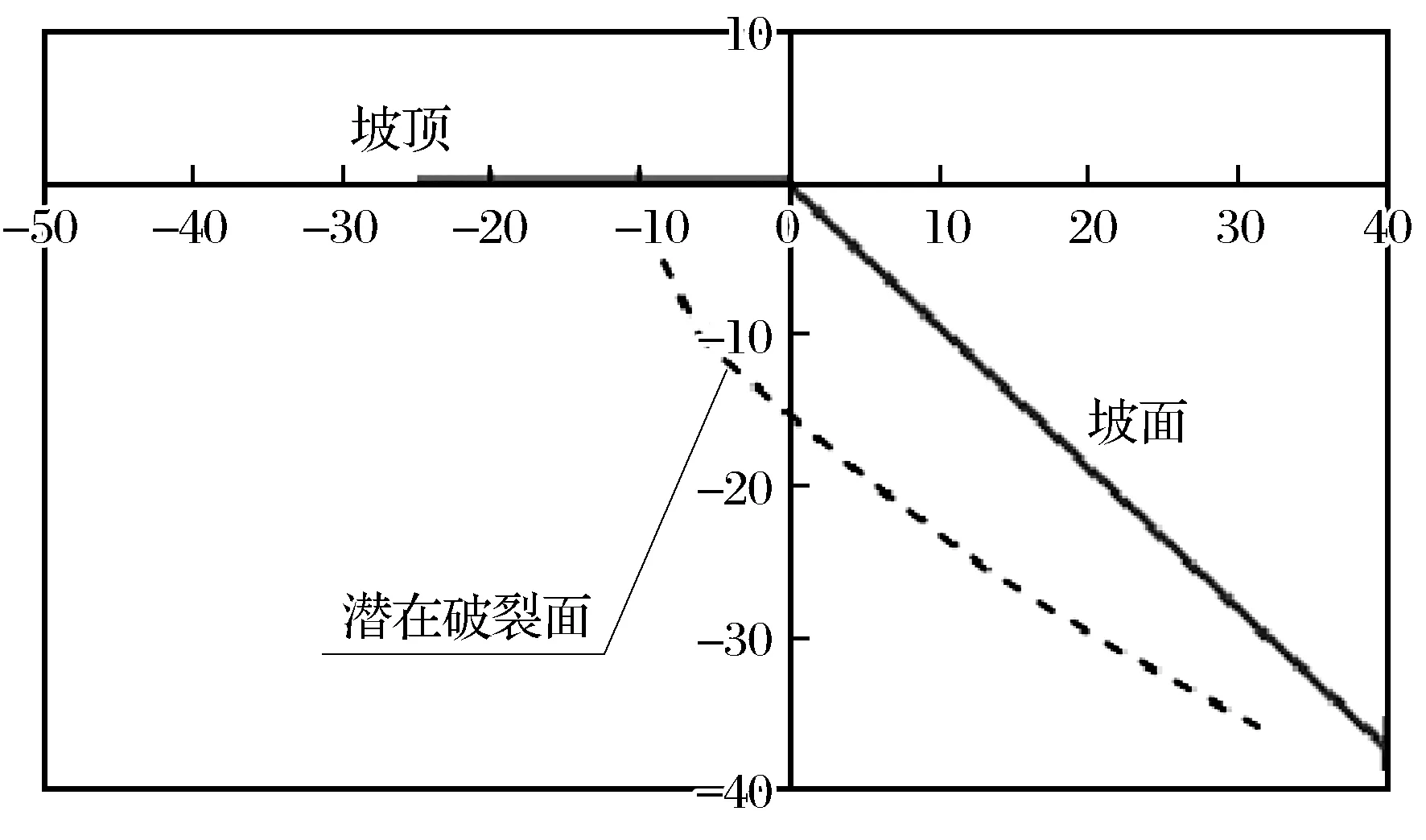
图3 模型A-1潜在破裂面Fig.3 Potential fracture plane of model A-1
由图3可知,模型A-1的内部破裂面为一条曲率较小的弧线。结合图2所示数据,模型中格栅最大应变不超过1.1%,因此可以看出模型A-1所模拟的边坡变形较小,基本稳定。
模型A-2的应变片全部布置在模型中轴面上。应变片传感器在中轴面上的分布情况如图4所示。
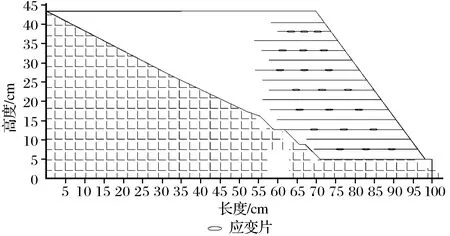
图4 模型A-2格栅应变片布置图Fig.4 Layout of strain gauge distribution of model A-2
由图4可知,应变片布置在模型格栅的四等分点。严格按设计的过程进行上机试验后,得到从底到顶的各层格栅在不同离心加速度下应变随距坡面距离的变化曲线(见图5)。
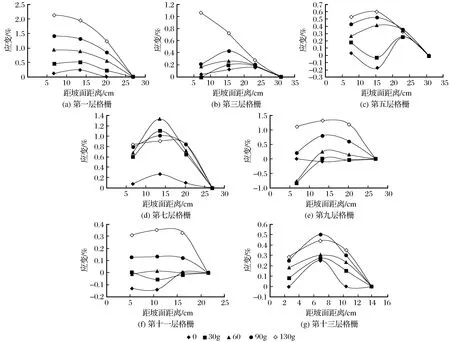
图5 模型A-2格栅在不同离心加速度下应变随距坡面距离的变化曲线Fig.5 Variation curve of strain changing with distance to slope of model A-2 under different centrifugal acceleration
将模型A-2所测各层模型格栅应变最大处连接可得出该模型中潜在破裂面大致位置如图6所示。
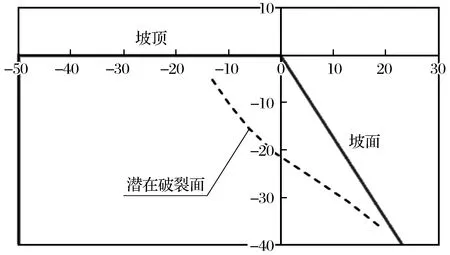
图6 模型A-2潜在破裂面Fig.6 Potential fracture plane of model A-2
通过对比图3和图6发现,模型A-2潜在破裂面的曲率略大于模型A-1破裂面,且相对模型A-1潜在破裂面,模型A-2的潜在破裂面更远离坡面,这说明在其他条件相同的情况下,模型A-2破裂面与坡面之间的面积大于模型A-1破裂面与坡面之间的面积,坡度越陡则其潜在的危害性越大。对比图2与图5可知,在离心加速度达到130g时,模型A-2的格栅各层的平均应变均大于对应的模型A-1的格栅各层平均应变,因此可以推测模型A-1所模拟的加筋边坡稳定性要强于模型A-2。在天然工况下,随着加筋土边坡坡度增大,潜在破裂面的曲率增大,同时出现由“圆弧形”向“折线型”转化的趋势,且破裂面具有向坡内移动的趋势。
2.2 孔隙水压力分布情况
模型A-1’、A-2’是在模型A-1、A-2试验完成的基础上再进行降雨模拟的模型。模型A-1’的孔隙水压力传感器全部布置在模型中轴面上。孔隙水压力传感器在中轴面上的分布情况如图7所示。
由图7可知,除K1号孔压传感器布置在底部筋材中部,其余的孔压传感器均布置在基覆界面。严格按设计的过程进行上机试验后,得到的土压力及离心加速度随时间的变化曲线如图8所示。
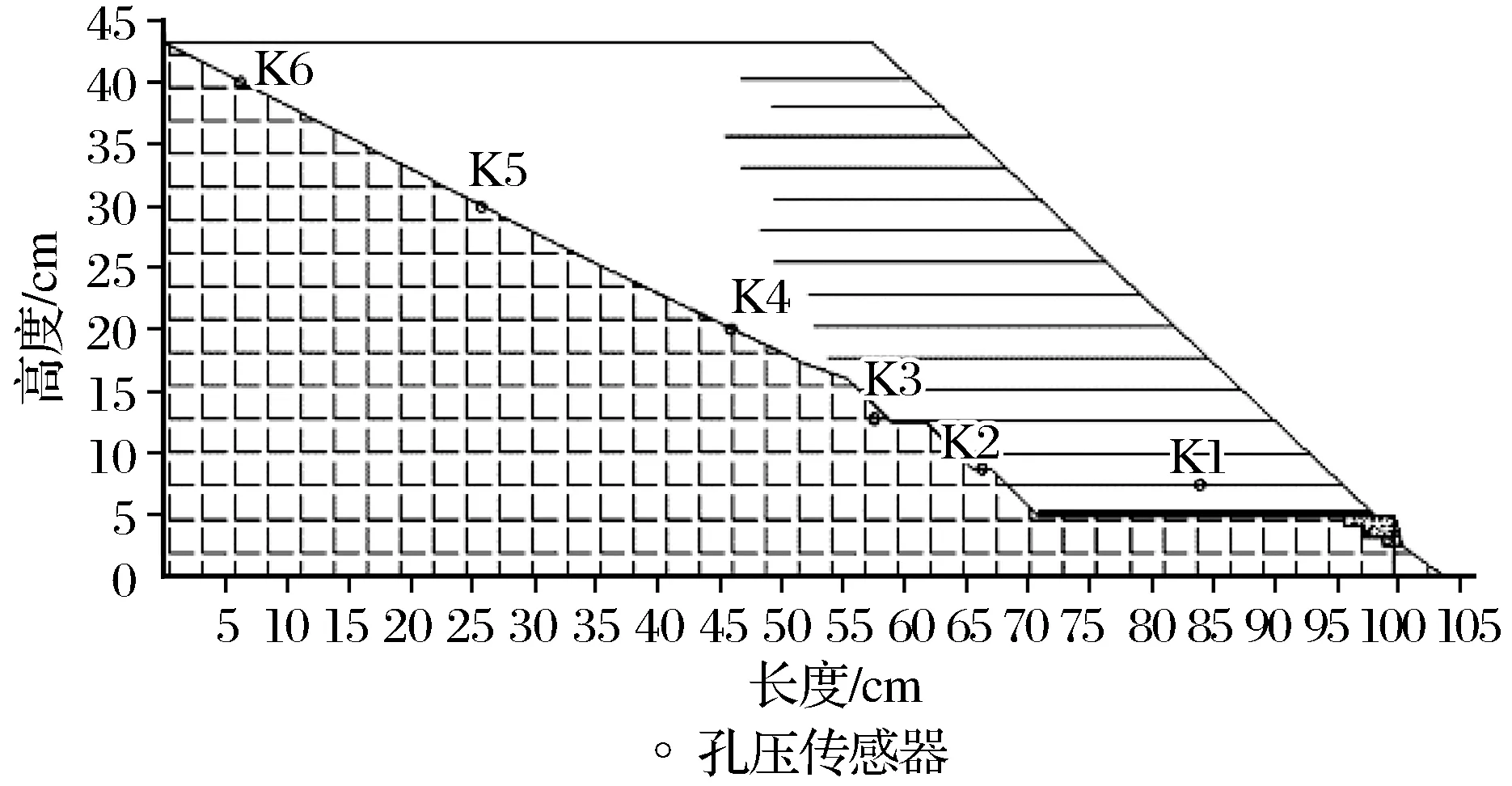
图7 模型A-1’孔隙水压力传感器布置图Fig.7 Pore-water pressure sensor of model A-1’
由图8可知,传感器K1(接近坡脚)处的平均孔隙水压力随降雨强度变化波动不大,在一级降雨开始时就达到45 kPa,一直到三级降雨开始一直保持缓慢增长的趋势,直到三级降雨结束开始缓慢下降,平均孔隙水压力达到51.5 kPa;传感器K2处的孔隙水压力在一级降雨开始直至卸载一直为49.1 kPa,由此估计该传感器后期读数异常;K3传感器在一级降雨开始直到四级降雨结束随着降雨强度逐级增加一直处于逐渐增大的趋势,从0直至四级降雨后的13.6 kPa;K4传感器对降雨的感应很小,基本保持为0,可见湿润峰并未达到K4所处位置;K5传感器从一级降雨开始孔隙水压力一直呈缓慢增加,从13.3 kPa一直增加到24.3 kPa;K6传感器数据对降雨的响应最为明显,一级降雨峰值孔压为15.3 kPa,二级降雨峰值孔压为16.9 kPa,三级降雨峰值孔压为18.2 kPa,四级降雨峰值孔压为17.9 kPa;K6传感器监测孔压随时间变化曲线与降雨随时间变化趋势相吻合,可见K6传感器所监测位置土体受降雨影响较大。
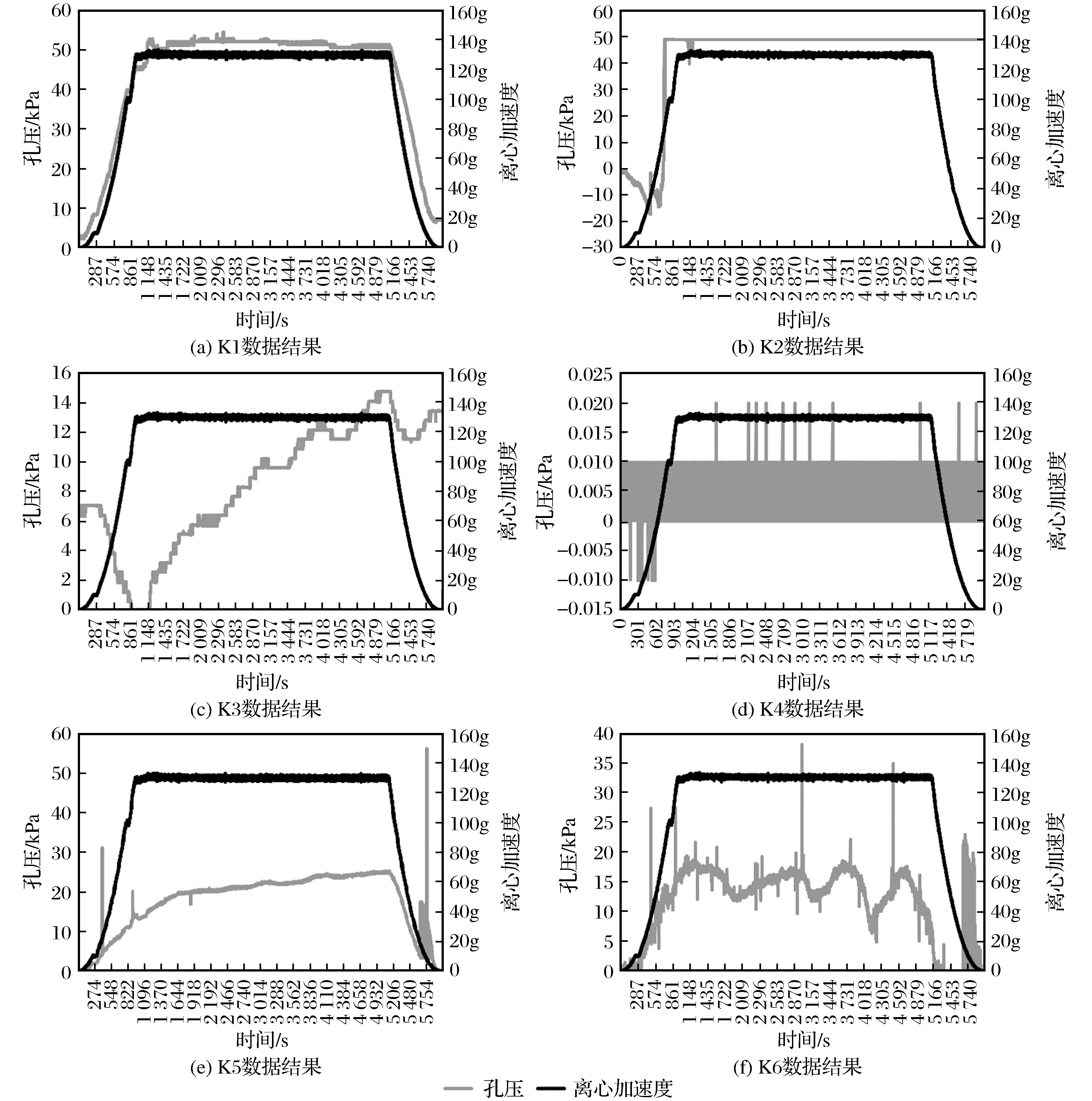
图8 模型A-1’不同位置处土压力及离心加速度随时间变化曲线Fig.8 Variation curve of pressure and centrifugal acceleration of model A-1’ with different time at different position
经过对比分析发现,各监测点孔压的平均值为K1>K2>K5>K6>K3>K4,可得该模型湿润峰已经达到基覆界面。对于这种分布,究其原因是降雨下渗到土体内部的主要途径有2种:一是通过坡顶向下渗流,如K6、K5、K4所示规律,越靠近坡顶位置受降雨影响越明显,但对于深层的孔隙水压力影响很小;二是通过坡面向坡内渗流,如K1、K2、K3所示规律。同样的,越靠近坡面位置受降雨影响越大。
K4所示孔压为0,经分析其原因为降雨深度影响范围有限,且干湿循环作用下,只有浅表层土体发育裂隙,为土体产生渗水通道,而深层土体相对完整,渗透性低,形成内部隔水层。A-2’模型出现相同现象原因相同,不再赘述。
模型A-2’的孔隙水压力传感器全部布置在模型中轴面上。孔隙水压力传感器在中轴面上的分布情况如图9所示。

图9 模型A-2’孔隙水压力传感器布置图Fig.9 Pore-water pressure sensor of model A-2’
除K7号孔压传感器布置在底部筋材中部外,其余的孔压传感器均布置在基覆界面。严格按设计的过程进行上机试验后,得到的孔隙水压力及离心加速度随时间变化曲线如图10所示。
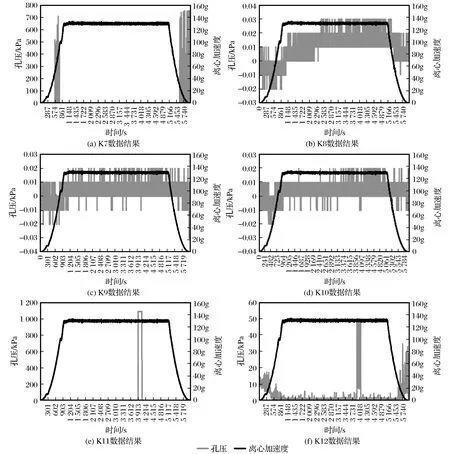
图10 模型A-2’不同位置处土压力及离心加速度随时间变化曲线Fig.10 Variation curve of pressure and centrifugal acceleration of model A-2’ with different time at different position
由图10可以发现,该模型内部传感器接触不良情况普遍,但是仍可从部分传感器读数中得到一些规律:首先,K7、K12两个传感器的孔隙水压力较大,K11传感器全程读数异常不做参考,而K8、K9、K10的读数为0,由此推测得出湿润峰未达到基覆界面深部转角处。经过分析发现,各监测点孔压的平均值为K7>K12>K8=K9=K10,可得该模型湿润峰已经达到基覆界面。
通过与模型A-1’试验对比,在同等降雨条件且其他条件相同的情况下,60°坡度的加筋土高填方边坡的湿润峰与43°坡度的加筋土高填方边坡内部的浸润区相比,60°坡度的浸润区更加靠近基覆界面。孔隙水压力的分布为坡脚>基覆界面顶部>基覆界面底部且坡脚处对分级降雨的响应最敏感。
2.3 模型变形分析
在离心试验过程中,变形的主要原因是离心加速度增加了土体自重,因而前期变形以竖向沉降为主。随着离心加速度的增加,边坡开始出现水平变形。坡面水平变形最先起自靠近坡脚处坡面,随后逐渐向上发展。主要垂直沉降出现在坡肩与靠近坡肩处坡面,主要水平变形出现在靠近坡脚处坡面,而在边坡内部变形较小。随着加速度的提高,在坡顶中部出现了一系列拉裂缝。为了对比不同变量离心模型试验的变形规律,现将主要变形现象总结见表3。

表3 离心模拟现象总结Table 3 Centrifugal simulation results
对比模型A-1与A-2发现,在天然工况下,填料相同的模型在边坡保持稳定的坡度范围内,坡顶裂缝的深度、展布范围与坡面鼓出变形量均与坡度正相关。在降雨工况下,模型A-1’稳定性良好,模型A-2’发生了失稳现象,可见雨水入渗不仅减弱了填料自身的抗剪强度以及与筋土之间的摩擦作用,还促进了原有裂缝向下延伸贯通,最终与坡体内部的潜在剪切破裂带贯通形成破坏面,同时雨水的入渗导致坡体内部的裂缝中产生水平推力,促使筋材从土体内拔出,最终失稳。加筋土边坡稳定性随坡度增加而减小,且降雨工况对稳定性的影响的敏感程度随坡度的增加而增大。在其他条件相同的情况下,加筋土边坡稳定性与坡度负相关。同时可以说明,坡度越陡的加筋土边坡对于降雨工况所产生的稳定性影响程度越敏感。
3 数值模拟验证
3.1 不同坡度下加筋高填方边坡稳定性分析
加筋土边坡与一般的天然边坡有很大不同,它是由筋-土复合材料组成的边坡,因此对于加筋边坡的分析要充分考虑筋土之间的相互作用。鉴于这种情况,加筋边坡的稳定性分析并不能通过一般的数学模型精确求解,需要用数值模拟软件进行有限元分析。研究采用PLAXIS数值模拟软件,在强度折减法与极限平衡法的基础上,对加筋填方边坡进行数值模拟,得到不同坡度加筋填方边坡剪应变云图(见图11)。
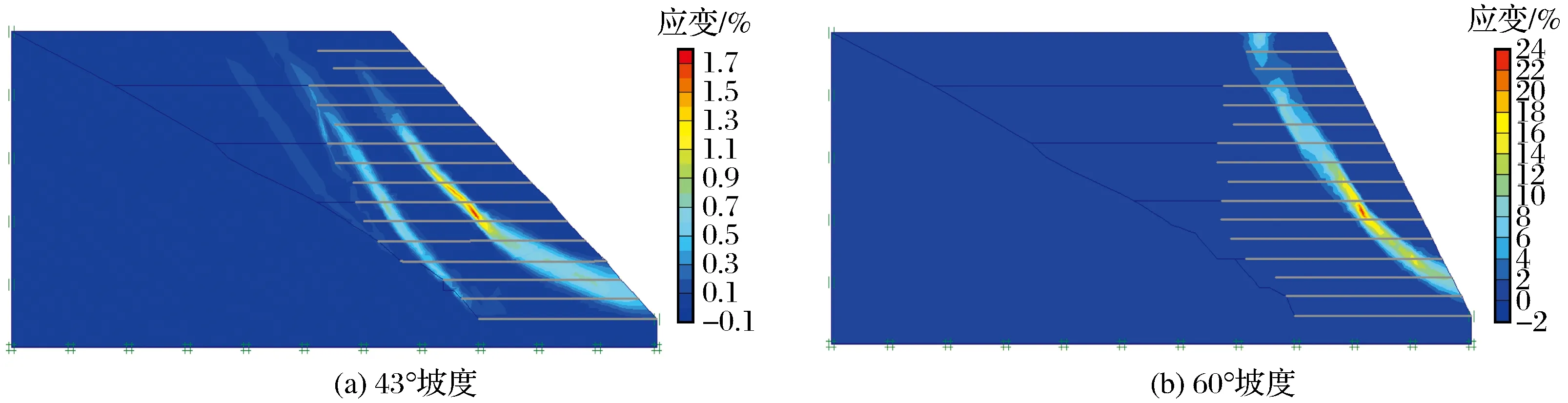
图11 不同坡度加筋填方边坡剪应变云图Fig.11 Cloud chart of slope shear stress at different reinforced fill slope
当坡度为43°时,坡体内的剪切带有3条:第1条在未加筋区,呈直线型;第2条在筋材末端,近似呈直线型;第3条在加筋区域中间,呈圆弧形,由坡脚向坡顶延伸。3条剪切带的贯通程度都较低,最大的剪应变点出现在第3条剪切带中间距坡底16.86~20.23 m高度的层间土中,剪应变达到1.8%。当坡度达到60°时,坡体内的剪切带只有1条且呈圆弧形,一端起自距坡脚10.12 m高度处,穿过加筋区中部达到距坡脚40 m高度处,另一端起自距坡肩15.2 m处,向下延伸,两端形成剪切带有贯通趋势,剪应变中心同样出现在剪切带中间距坡底16.86~20.23 m高度的层间土中,最大剪应变达到24%。通过对比可以发现,随着坡度的增大,坡体内部的剪应变带趋于集中、贯通,曲率逐渐增大,且有向“0.3H折线形”转换的趋势,剪切破坏带的剪应变也随坡度增加而增大,剪应变最大值中心也会增多。同时可以发现加筋土内部的破裂面往往发源于层间土,之后再向加筋处延伸贯通。
由数值模拟可以发现,所有模型剪应变最大值出现在坡脚附近的筋间土中,可以推测加筋土的破裂面延展模式为“坡脚筋间土剪切破坏-破裂面向上延展贯通,穿透格栅-破裂面与坡顶张裂缝贯通形成破坏带-沿破坏带失稳”。
3.2 降雨工况下对加筋高填方边坡数值模拟
为了系统地对降雨工况下不同坡度下加筋高填方边坡的内部孔压分、渗流状态与稳定性影响进行分析,研究运用Geostudio数值模拟软件,采用以达西定律为理论基础的SEEP/W模块与以极限平衡理论为基础的SLOPE/W模块相耦合的方式进行分析计算。为了对应离心模型试验的降雨条件,对数值模型采用瞬态渗流边界条件,边界条件函数与降雨历程相吻合。
将A类填料降雨工况下的不同坡度的加筋边坡孔隙水压力与渗流矢量结果总结见表4。
在相同的条件下,不同坡度模型内部的孔隙水压力分布状况与渗流矢量分布区别很大。对于43°坡度模型,其孔压分布云图呈同心圆状,渗流中心在坡体内部,在降雨结束后,孔压较小的非饱和区域内缩,饱和区域增大,致使模型内部孔压分布在基覆界面出现了坡脚>基覆界面与坡顶相交处>基覆界面中部的情况,这一点与离心模型试验结果吻合。在降雨间歇期,坡肩位置的孔隙水压力消散最为明显;而对于60°坡度模型,其孔压分布云图自坡顶到坡底呈层状分布,渗流中心在坡脚位置,基覆界面处的孔压分布出现了坡脚>基覆界面中部>基覆界面与坡顶相交处的情况,这与离心模型试验结果有一定差别,分析误差原因主要有两点:一是经过天然工况下的试验,边坡土体被压密,性质出现改变;二是边坡内部产生了一系列微裂隙,在试验过程中贯通产生了新的渗流通道,与43°坡度模型相同之处是在降雨间歇期孔隙水压力消散最明显区域为坡肩处。
通过表4的结果对比可得,在其他条件相同的情况下,随着坡度增加,坡体孔压分布等值线由同心圆形逐渐转换成层状,渗流中心随坡度增加存在“坡体中心位置-坡脚位置-基覆界面水平斜面交界处”移动趋势。
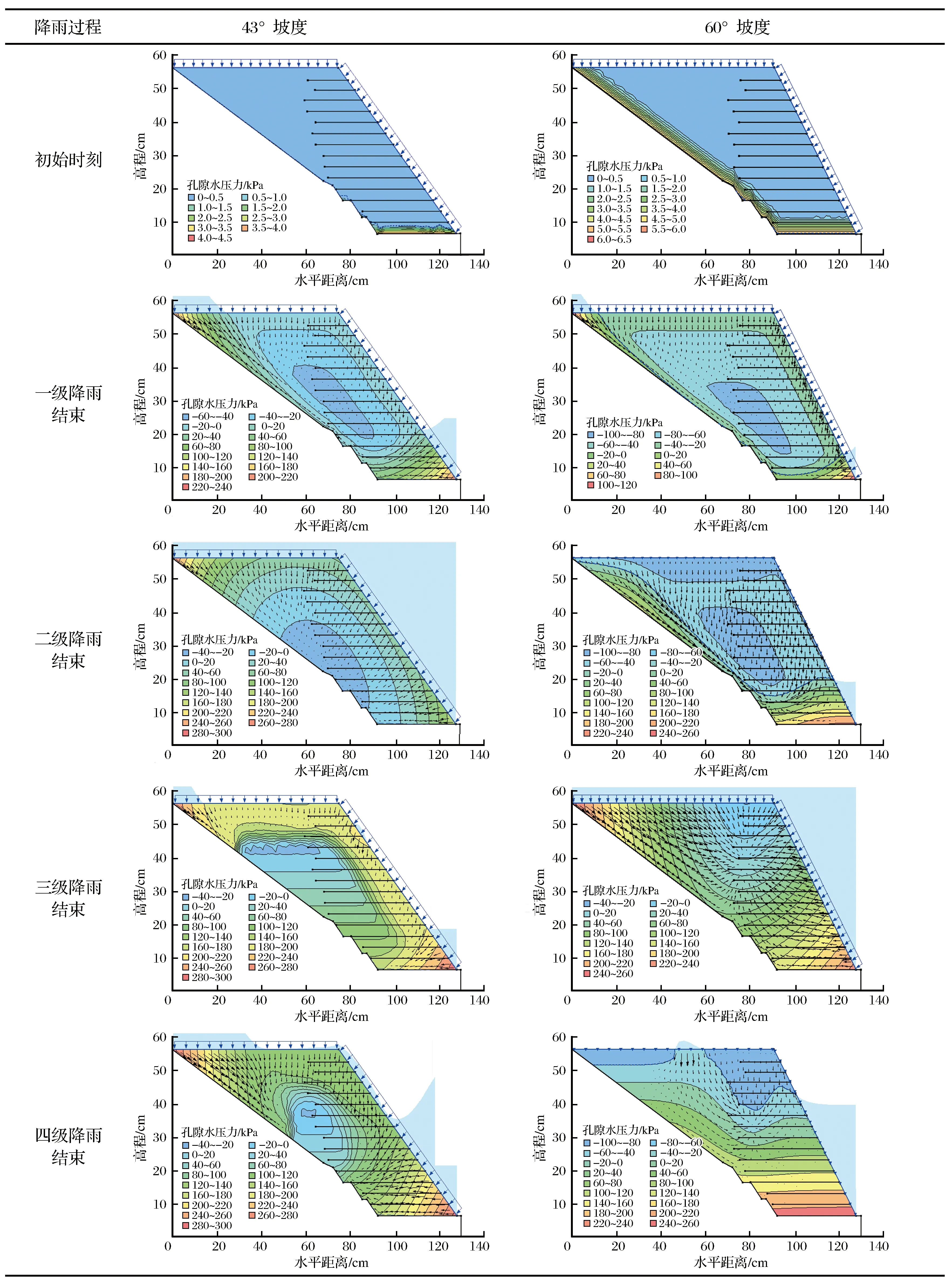
表4 不同坡度模型在各级降雨过程中孔压分布与渗流矢量Table 4 Pore pressure distribution and vadose vector of different slope model at different rainfull level
为研究降雨工况下,坡度对潜在滑移面位置及稳定性系数的影响,利用数值模拟软件分别对43°、60°与72°三种坡度的加筋边坡稳定性进行了数值模拟计算,降雨工况下不同坡度加筋边坡潜在滑移面见图12,降雨工况下边坡稳定系数对比见图13。
由图12分析可知,在降雨和其他条件相同的情况下,43°加筋坡体的临近滑动面靠近坡面位置,且滑面剪出位置在坡面中下部位置;60°加筋坡体的临界滑面大致处于坡体中间位置,滑面剪出位置在坡脚区域;72°加筋坡体的临界滑面更靠近基覆界面位置,滑面剪出位置在坡脚区域。由此可得,随着坡度的增加,加筋边坡的潜在滑动面的位置有向坡内移动的趋势,滑面剪出位置由坡面下方区域转向坡脚。由图13可知,三种坡度的稳定性系数在初始时刻即未降雨时刻最大,分别为1.58、1.19、1.08,当坡度越陡,稳定性系数也随之减小;在四级降雨的过程中,稳定性系数逐渐减小,随着降雨强度越来越大,曲线的斜率变大,即稳定系数的变化幅度变大。

图12 降雨工况下不同坡度加筋边坡潜在滑移面Fig.12 Potential sliding surface of different reinforced soil slope under rainfull condition
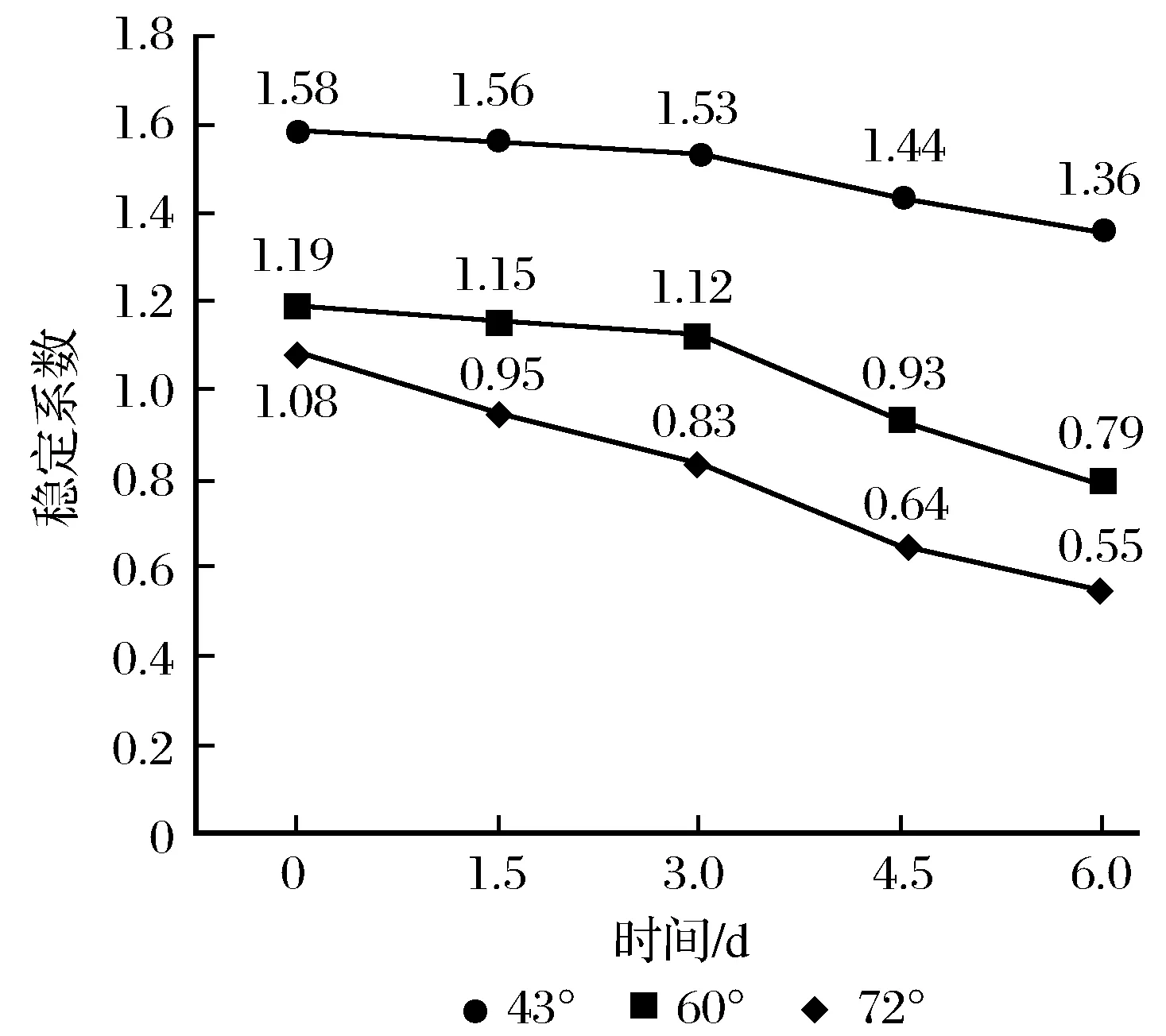
图13 降雨工况下边坡稳定系数对比Fig.13 Comparison of slope stability coefficient underrainfull condition
4 结论
以重庆巫山机场2号沟加筋高填方边坡为原型,以离心模拟与数值模拟为研究手段,以室内试验数据作为基础数据,以坡度、工况两方面对加筋高填方边坡稳定性影响进行探究。研究得到以下主要结论及工程建议:
(1) 无论是在天然工况还是降雨工况下,加筋边坡稳定性与坡度之间都存在近似线性的负相关关系,但在降雨工况下,加筋边坡稳定性对坡度变化带来的影响更加敏感。
(2) 通过离心模拟与数值模拟综合对比可以看出,在天然工况下,随着坡度的增加,潜在破裂面的曲率逐渐增加;整体来看,随着坡度增大,加筋边坡潜在破裂面存在由“圆弧形”向“0.3H折线形”转化的趋势。
(3) 在基覆界面模型内部孔压分布为坡脚>基覆界面顶部>基覆界面底部。坡脚处对分级降雨的响应最敏感。在其他条件相同的情况下,随着坡度增加,坡体孔压分布等值线由同心圆形逐渐转换成层状,渗流中心随坡度增加存在“坡体中心位置-坡脚位置-基覆界面水平斜面交界处”移动趋势。
(4) 加筋边坡的剪应变最大处往往出现在坡脚与坡中内部的筋间土,在实际工程中,应适当增大坡脚附近加筋的密度或强度,以抑制剪应变带来的扩展。对于高陡加筋边坡,由于其位移中心向坡肩转移,因此坡肩位置更容易发展形成深宽张裂缝,在这种情况下,在坡肩处应适当加长布筋长度,并使用强度较高的筋材。在降雨工况下,坡脚位置往往容易出现雨水聚集,因此在坡脚位置应当加强排水设施的设置。

