中心部分分段Halbach永磁同步轮毂电机解析计算与优化设计

高锋阳,李明明,齐晓东,杨乔礼,陶彩霞

(兰州交通大学自动化与电气工程学院,730070,兰州)

永磁同步电机(PMSM)以其效率高、体积小、结构多样化、过载能力强等优点成为轮毂电机的首选[1-4]。然而,由于转矩脉动过大会造成PMSM输出转矩平滑度过低,不仅会产生振动和噪声,而且影响机车系统的控制精度。可以从两个方面抑制转矩脉动:一方面,电机在反馈控制条件下,转速环和电流环通过抑制纹波转矩脉动来抑制电磁转矩脉动;另一方面,电机在输入电流为标准正弦波时,不存在由于时间谐波造成的纹波转矩脉动,而是以空间谐波产生的齿槽转矩脉动为主,可以通过优化电机本体结构参数降低齿槽转矩脉动,进而抑制电磁转矩脉动。

从PMSM齿槽转矩产生的机理出发,削弱齿槽转矩的方法主要可归纳为三大类,即改变永磁体磁极参数、改变电枢参数[5]以及合理组合电枢槽数和极数[6],其中改变永磁体磁极参数的方法效果最显著。文献[7]通过优化磁极结构,把减小气隙磁密谐波分量作为削弱齿槽转矩的依据,分析了不同转子磁极优化技术的优缺点。文献[8]提出了两种凸形不等厚磁极结构来降低气隙磁密谐波畸变率和齿槽转矩,结果表明采用不等厚磁极可以有效增大电磁转矩,但未分析对电机转矩脉动的影响。文献[9]采用偏心磁极结构来优化表贴式PMSM气隙磁密波形,并结合样机试验证明了计算方法的准确性,但制造工艺复杂。优化磁极结构虽可以削弱齿槽转矩,但会造成电机磁场畸变,增大电机气隙磁场分布计算和优化的难度。

气隙磁场的求解方法主要分为数值法、解析法[10]以及数值解析结合法[11]。其中,解析法因其参数间关系简洁明了,便于分析计算,所以应用最广。文献[12]采用保角变换法推导出复相对磁导函数,得到完整的气隙磁场分布,但求解过程复杂,无法考虑槽间相互影响,不利于反电势的精确计算。精确子域模型法能够考虑定子槽间相互影响,可以根据材料属性和电机结构将电机划分为不同的子域,在计算电磁性能方面具有较高的精度。文献[13]在导磁材料磁导率为给定值的情况下,采用精确子域模型法推导了电机气隙磁密、空载反电动势及输出转矩的表达式,研究了极弧系数和槽开口宽度对输出转矩的影响,但所建模型槽型尺寸仅由槽口宽度决定,实用性较差。文献[14]在精确子域模型法的基础上对永磁体做了等效分块处理,推导了偏心削极磁极平行充磁电机空载运行时的气隙磁密解析表达式,但利用微元思想简单将偏心磁极结构等效为瓦片式结构的叠加使计算结果受分块精度的影响。

此外,轮毂电机处于密闭空间,永磁体产生的涡流损耗(PECL)会使其自身产生高温,面临不可逆退磁的风险。降低永磁体涡流损耗主要从永磁体的材料和结构出发。文献[15]设计了一种偏心磁极结构来降低永磁体涡流损耗,并通过温度场分析证明采用这种偏心磁极结构能够有效降低单位体积的涡流损耗和永磁体的稳态温度。文献[16]设计了一种Halbach充磁方式的部分分段永磁体结构,经仿真验证Halbach部分分段结构能够降低永磁体涡流损耗。文献[17]提出一种永磁体环形部分分段结构,与单侧部分分段结构和双侧部分分段结构相比,环形结构降低永磁体中涡流损耗的效果更好,且保证了永磁体的机械鲁棒性。

本文从电机本体出发,提出一种主磁极中心部分分段结构,推导出主磁极中心部分分段永磁同步电机计及定子开槽效应下的气隙磁密解析表达式,计算出电机的齿槽转矩和电磁转矩,并通过有限元仿真验证解析结果的准确性;提出分级优化思想,通过对不同等级下电磁性能仿真结果的分析,确定相应的优化目标;系统分析定子槽开口宽度、极弧系数、主磁极宽度和厚度、边界磁极厚度、剖去部分的宽度和深度对气隙磁密基波幅值和谐波畸变率、转矩脉动(Tr)、单位体积永磁体产生的电磁转矩(Tavg)、单位体积永磁体产生的涡流损耗(PECL,uv)的影响,确定其最优结构参数,并与相关8种电机结构的电磁性能进行对比。

1 模型解析

在二维极坐标系下,建立如图1所示电机解析模型。采用精确子域模型法分析定子开槽下的气隙磁场分布。为便于分析计算,做出如下假设:①永磁体材料具有线性退磁特性;②忽略端部影响;③铁磁材料磁导率无穷大。

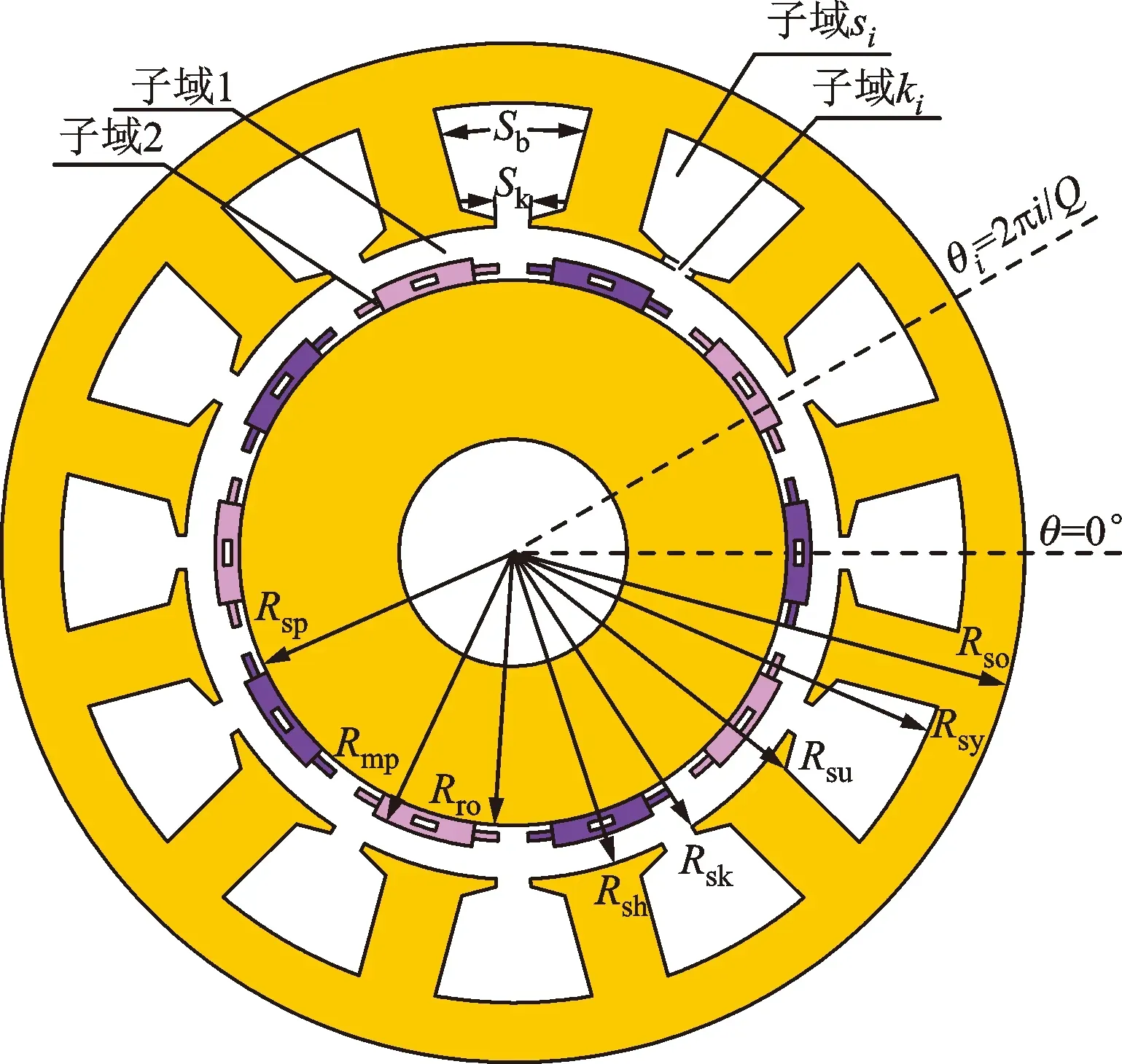
(a)空载解析模型

图1中,θi=2πi/Q,为第i槽初始角度,Q为定子槽数,Rso为定子外半径,Rsy为定子槽底半径,Rsu为定子槽顶半径,Rsk为定子槽口外半径,Rsh为定子内半径,Rmp为主磁极外半径,Rsp为边界磁极外半径,Rro为转子轭外半径,Sb为槽身角度,Sk为槽口角度,Rsk=Rsu-lfoot+lfoot1(lfoot为定子齿足高度,lfoot1为定子槽口高度)。图1a所示空载气隙磁场解析模型在二维极坐标系下划分为4个子域:气隙、永磁体、第i个槽口、第i个槽身,即分别为子域1、2、ki、si。图1b所示电枢反应磁场解析模型在二维极坐标系下划分为3个区域:等效气隙、第i个槽口、第i个槽身分别为子域Ι、Ki、Si。

图2a所示为三块式Halbach型磁钢在一对极下的充磁表示,Wmp为主磁极极弧长度,Wsp为磁极总极弧长度,Wp为极距,p为极对数。定义主磁极极弧系数为αmp=Wmp/Wp,边界磁极极弧系数为αsp=Wsp/Wp。图2b所示为待优化十字型主磁极中心部分分段磁极结构,lmp为主磁极厚度,lsp为边界磁极厚度,lcp为中心剖去部分厚度,Wcp为中心剖去部分极弧长度。

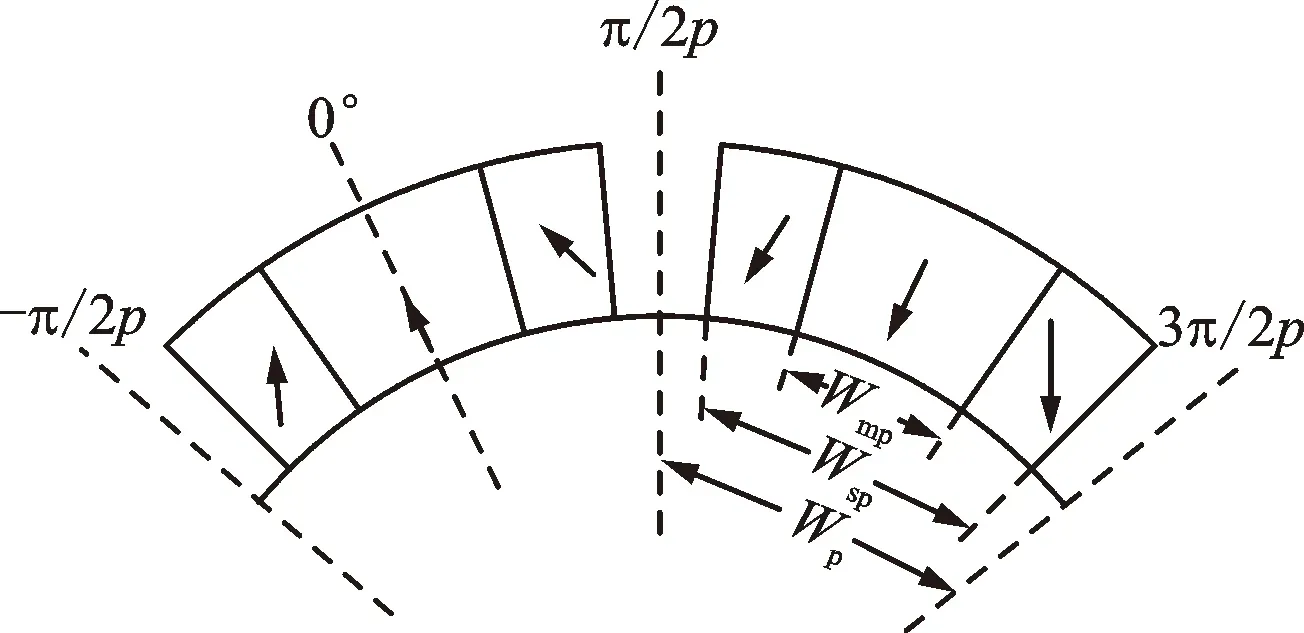
(a)三块式Halbach型磁钢

(b)十字型主磁极中心部分分段Halbach(S9)结构图2 永磁体结构参数Fig.2 Structure parameters of rotor magnet permanent

2 磁场分析

2.1 空载磁场分析

空载气隙磁场计算的一般方程为

(1)

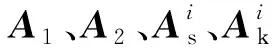
各子域气隙磁密和磁场强度关系为

(2)

各子域边界面上满足如下边界条件

(3)

定义如式(4)所示函数关系式,用来简化各子域矢量磁位通解、待定系数及谐波系数的表达式。

(4)

由分离变量法得各区域矢量磁位通解表达式如式(5)～式(8)所示。

(C1nrng+D1nr-ng)sin(ngθ)]

(5)

(C2nrng+D2nr-ng)sin(ngθ)]+

(6)

(7)

(8)

式中:n、j、m分别为子域1和2、子域ki、子域si内矢量磁位的谐波次数;g为p和Q的最大公约数。

2.1.1 空载气隙磁密 由矢量磁位与磁通密度满足的关系,可得空载气隙磁密的径向和切向表达式

(C1nrng-1+D1nr-ng-1)ngcos(ngθ)]

(9)

(10)

表1所示为十字型主磁极中心部分分段Halbach PMSM结构空载气隙磁密分布。

表1 十字型主磁极中心部分分段Halbach结构空载气隙磁密分布

表1中,Brp1是极弧系数为Wsp/Wp、内外径分别为Rro和Rsp的永磁体单独作用时产生的气隙磁场;Brp2是极弧系数为Wmp/Wp、内外径分别为Rro和Rsp的永磁体单独作用时产生的气隙磁场;Brp3是极弧系数为Wsp/Wp、内外径分别为Rro和Rsp-lsp的永磁体单独作用时产生的气隙磁场;Brp4是极弧系数为Wmp/Wp、内外径分别为Rro和Rsp-lsp的永磁体单独作用时产生的气隙磁场;Brp5是极弧系数为Wmp/Wp、内外径分别为Rro和Rmp的永磁体单独作用时产生的气隙磁场;Brp6是极弧系数为Wcp/Wp、内外径分别为Rro和Rmp-lmp/2+lcp/2的永磁体单独作用时产生的气隙磁场;Brp7是极弧系数为Wcp/Wp、内外径分别为Rro和Rmp-lmp/2-lcp/2的永磁体单独作用时产生的气隙磁场。

2.1.2 齿槽转矩 根据空载气隙磁密分布计算结果,利用麦克斯韦应力张量法,齿槽转矩Tcog为

(11)

式中:Lz为电机轴向长度;r为位于气隙中运动边界内的任意圆周半径。

2.2 电枢反应磁场分析

采用如式(12)所示正弦交流电作为激励源,根据电机模型中A相轴线与d轴的初始夹角θcs确定所加电流源激励的初始相位φ=θcspπ/180。

(12)

式中:iA、iB、iC分别为A、B、C三相瞬时电流值;Im为相电流有效值。

电枢反应磁场计算时,永磁体不充磁,加电流源激励后磁场计算的一般方程为

(13)

式中:AΙ、AKi、ASi分别为子域Ι、Ki、Si内矢量磁位;Ji为第i槽内绕组的电流密度。

各子域边界条件为

(14)

由分离变量法得各子域矢量磁位通解表达式

(CΙnrng+DΙnr-ng)sin(ngθ)]

(15)

(16)

ASi=ASi0+ACi(r)+

(17)

式中:

(18)

(19)

由矢量磁位与磁通密度满足的关系,可得等效气隙磁密表达式

(CΙnrng-1+DΙnr-ng-1)ngcos(ngθ)]

(20)

(CΙnrng-1-DΙnr-ng-1)ngsin(ngθ)]

(21)

式中:AΙn～DΙn、AKi0、BKi0、AKij、BKij为电枢反应气隙磁场待定系数。

2.3 负载磁场分析

2.3.1 负载气隙磁密 由叠加定理可得

(22)

2.3.2 电磁转矩 根据负载气隙磁密分布计算结果,利用麦克斯韦应力张量法,电磁转矩Tem的表达式为

(23)

式中:re为计算电磁转矩积分半径。

3 十字型中心部分分段结构有限元仿真验证与分级优化

对十字型主磁极中心部分分段Halbach PMSM模型进行有限元仿真分析。图3所示为1/2PMSM模型图。永磁体采用Halbach充磁方式,每极分为3块,边界磁极与主磁极不等厚不等宽。为降低转矩脉动和涡流损耗,得到更加正弦的气隙磁密波形,对主磁极中心部分分段,电机模型的主要参数如表2所示。当非永磁体参数固定时,分析气隙磁密解析表达式可知,主磁极中心部分分段Halbach PMSM的负载气隙磁密只与αsp、Rmp、Rsp、αmp、Wcp和lcp有关。当αsp、Rmp、Rsp以及αmp固定时,负载气隙磁密与lmp、lsp、Wcp和lcp有关。因此,对负载气隙磁密的优化主要是对lmp、lsp以及θcp和lcp的优化。

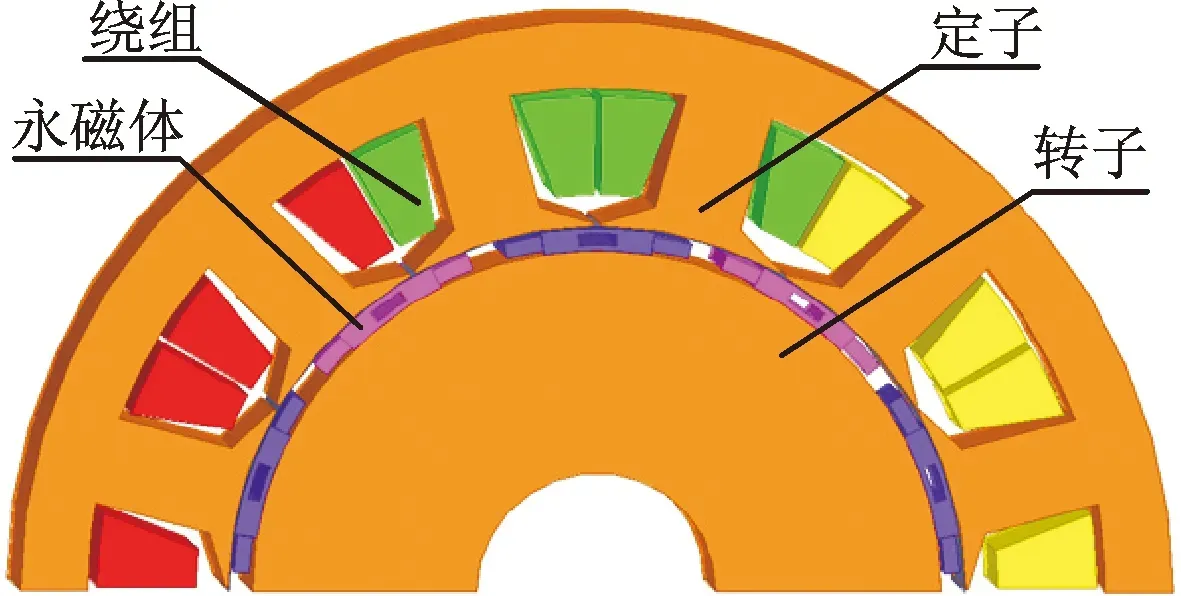
图3 十字型主磁极部分分段Halbach PMSM模型图Fig.3 Schematic diagram of cross-shaped Halbach PMSM with main magnetic pole central partially-segmented

表2 十字型主磁极中心部分分段Halbach PMSM主要结构参数

3.1 解析模型有限元仿真验证

对十字型主磁极中心部分分段Halbach PMSM的解析模型进行有限元仿真,得到图4所示空载齿槽转矩对比图和图5所示负载径向气隙磁密对比图。对于10极12槽PMSM,一个齿距内齿槽转矩的周期数为5[18]。因此,有限元仿真时将模型运动速度设置为1(°)/s,得到图4所示结果。

图4 齿槽转矩解析解与有限元结果对比Fig.4 A comparison of cogging torque between analytical solution and FEA

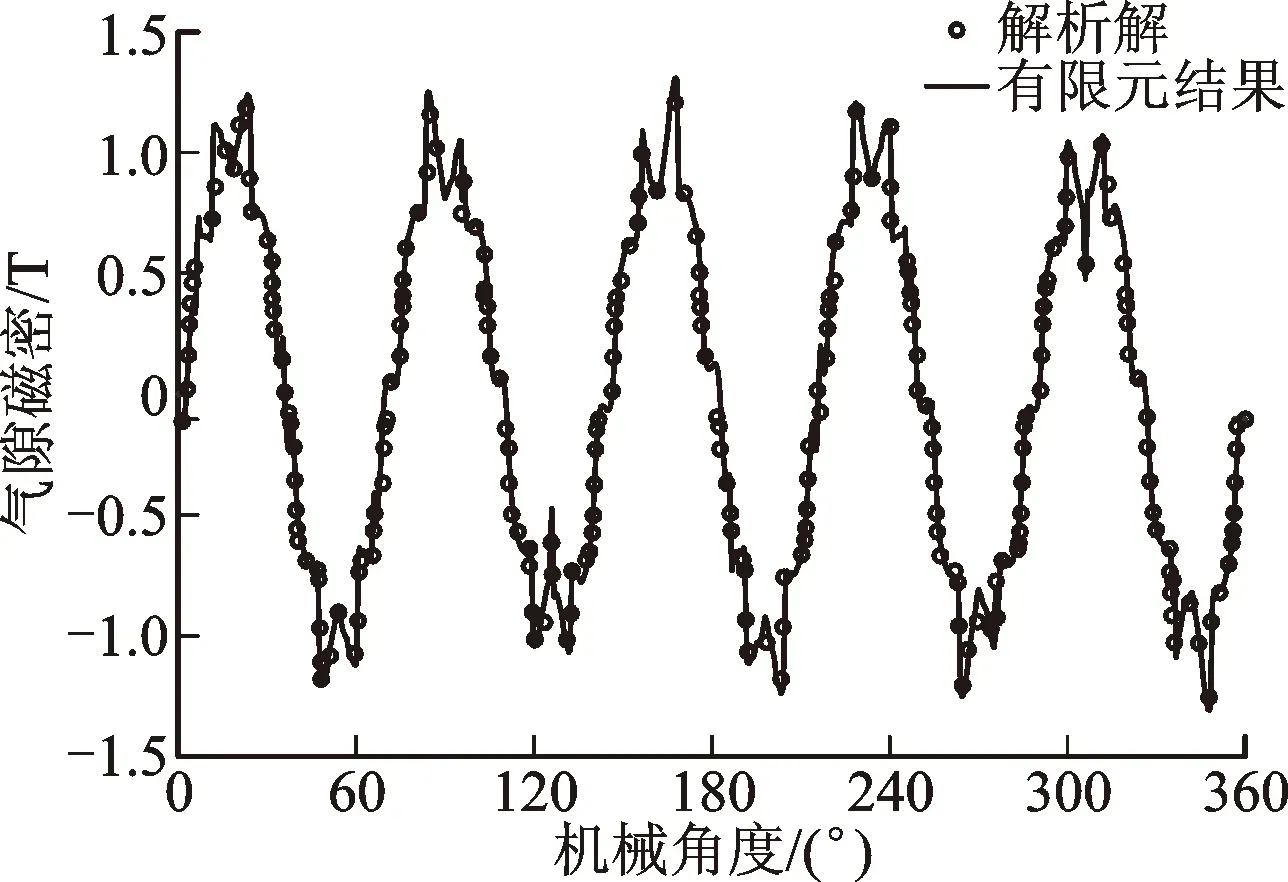
图5 负载气隙磁密解析解与有限元结果对比Fig.5 A comparison of magnetic flux density between analytical solution and FEA

如图4、图5所示,解析解和有限元分析结果基本吻合,即有限元仿真分析验证了解析方法的正确性。这为十字型主磁极中心部分分段Halbach PMSM的优化奠定了基础。

3.2 分级优化过程

有限元软件进行仿真分析时,仿真时间步长和参数取值步长直接影响仿真结果的准确性和有效性。对此,提出一种新的分级优化思想:首先,对要优化的结构参数进行分级组合;其次,在每一级的优化中,先对相关参数进行大范围大间隔的仿真分析,通过分析负载气隙磁密谐波畸变率、转矩脉动、电磁转矩以及涡流损耗的变化曲线,选择受参数变化影响较大的电磁性能作为本级优化目标,并根据优化目标缩小参数范围;最后,对相关参数进行小范围小间隔的仿真分析,依优化目标确定本级相关参数的最优组合,应用到电机结构中,为下一级优化做准备。

在负载工况下,按表3所示流程对定子槽口角度θk和永磁体极弧系数αsp进行一级优化。θk和αsp按表3组合1所示进行联合仿真,以负载气隙磁密谐波畸变率最小为优化目标,进一步对表3组合2进行优化得到如图6所示负载气隙磁密谐波畸变率变化曲线。

表3 一级优化流程

图6 负载气隙磁密谐波畸变率变化曲线Fig.6 THD variation curve of load air gap magnetic density

(a)0°～90°

考虑到定子模型为开槽结构,选取θk为1°,αsp为0.833 4(即永磁体总角度为30°)进行二级优化。考虑到边界磁极充磁角度θmag对气隙磁密的影响最大,所以在二级优化中只分析负载气隙磁密。首先,令边界磁极的充磁角度θmag在0°～90°内,每隔10°取一个值,得到图7a所示负载气隙磁密基波幅值和谐波畸变率随θmag的变化曲线。然后,为了更清楚地观察气隙磁密谐波畸变率波形拐点,令边界磁极的充磁角度θmag在0°～20°内,每隔5°取一个值,得到图7b所示气隙磁密谐波畸变率随θmag变化曲线。从图中可以看出,随θmag的增大,气隙磁密谐波畸变率先减小再增大,而气隙磁密基波幅值一直减小。当θmag=0°时,气隙磁密基波幅值有最大值1.019 T;当θmag=10°时,气隙磁密谐波畸变率有最小值21.6%,气隙磁密基波幅值为1.013 T。以气隙磁密谐波畸变率最小为目标,选取10°作为边界磁极的充磁角度,进行表4所示三级优化流程。

(b)0°～20°图7 负载气隙磁密谐波畸变率和基波幅值随θmag的变化Fig.7 Curve of THD and fundamental wave amplitude with θmag

表4 三级优化流程

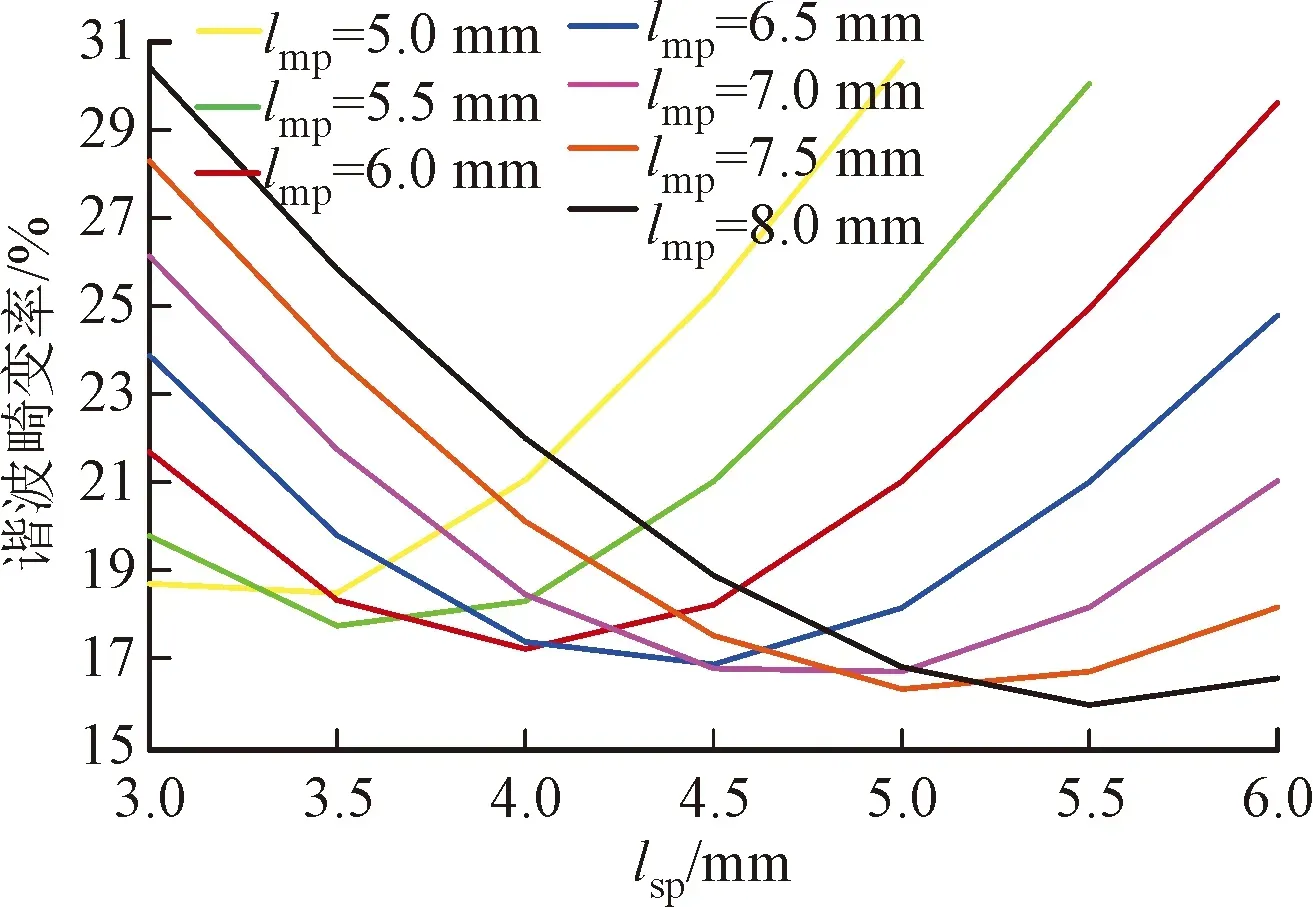
以谐波畸变率最小原则,对组合1、2、3进行优化。首先确定θmp的最优参数,进而对组合4中lmp和lsp展开联合优化,此时综合考虑对气隙磁密谐波畸变率、转矩脉动Tr、单位体积永磁体产生的电磁转矩、单位体积永磁体产生的涡流损耗这4个目标的影响,得到如图8所示曲线图。

(a)负载谐波畸变率曲线图

由图8a可知,当lmp固定时,随lsp增大,谐波畸变率先减小后增大;由图8b可知,随lmp的增大,Tr受lsp的影响越来越小。综合图8c和图8d可知,单位永磁体体积转矩呈整体下降趋势,表明增多的永磁体体积所占原有体积的比例比增大的转矩占原有转矩的比例高,lmp与Te呈反比,ls与Te呈正比。综合图8e和图8f可知,单位永磁体体积涡流损耗先减小后增大,表明增大边界磁极的厚度对涡流损耗影响较大。lmp与涡流损耗呈反比,lsp与涡流损耗呈正比。综合图8得出,lsp对电机电磁性能影响较lmp大,且气隙磁密谐波畸变率和Tr是影响电机整体性能的两个主要指标,这与实际应用中的结论一致。

结合三级优化结果和实际加工成本确定主磁极厚度lmp为7.5 mm,边界磁极厚度lsp为5 mm,并应用于电机模型。按照表5所示流程对主磁极中心剖去部分进行优化,考虑到永磁体主磁极的完整性及其机械强度,lcp不能超过主磁极厚度的65%,在表5组合1的参数组合中主磁极中心剖去部分深度lcp最大取4.8 mm。

表5 四级优化流程

对表5中的组合1进行优化,得到如图9所示仿真结果。永磁体的体积随lcp和θcp的增大而减少,对应图9c和图9e中的转矩和涡流损耗呈下降趋势。但图9d所示单位体积转矩随lcp和θcp的增大呈上升趋势。当θcp在9°～18°之间时,各项电磁性能受lcp的影响较θcp大。当θcm在3°～9°之间时,各项电磁性能受θcp的影响较lcp大。综合考虑负载气隙磁密谐波畸变率、转矩脉动及涡流损耗这3个目标,最终确定表5组合2的参数组合。

(a)负载谐波畸变率曲线图

(a)负载谐波畸变率曲线图

对表5中组合2进行优化得到图10所示仿真结果。可以看出,气隙磁密谐波畸变率、涡流损耗及转矩脉动变化较明显。中心部分分段的主要目的是降低涡流损耗,将涡流损耗作为第一优化目标,并保证气隙磁密谐波畸变率和转矩脉动变化不大。最终确定主磁极中心剖去部分角度θcp为4°,剖去深度lcp为2.3 mm。

图11为最优十字型主磁极中心部分分段Halbach结构的负载磁链、涡流损耗、反电势波形图以及A相反电势频谱图。

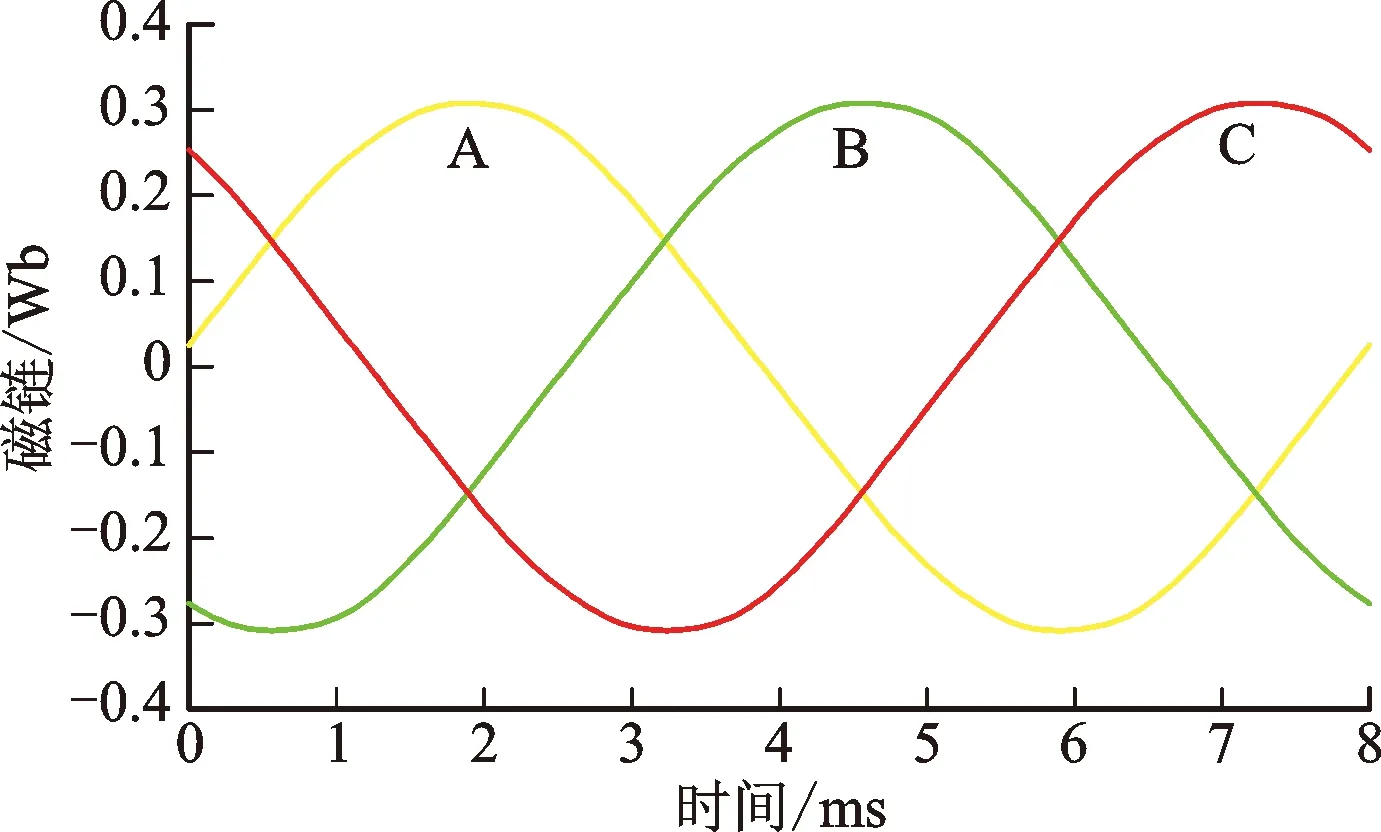
(a)磁链波形图

4 电磁仿真分析与比较

在十字型主磁极中心部分分段结构(S9)分级优化的基础上,采用同样的优化方法对表6所示8种结构分别进行优化,并对各项电磁性能进行对比分析。

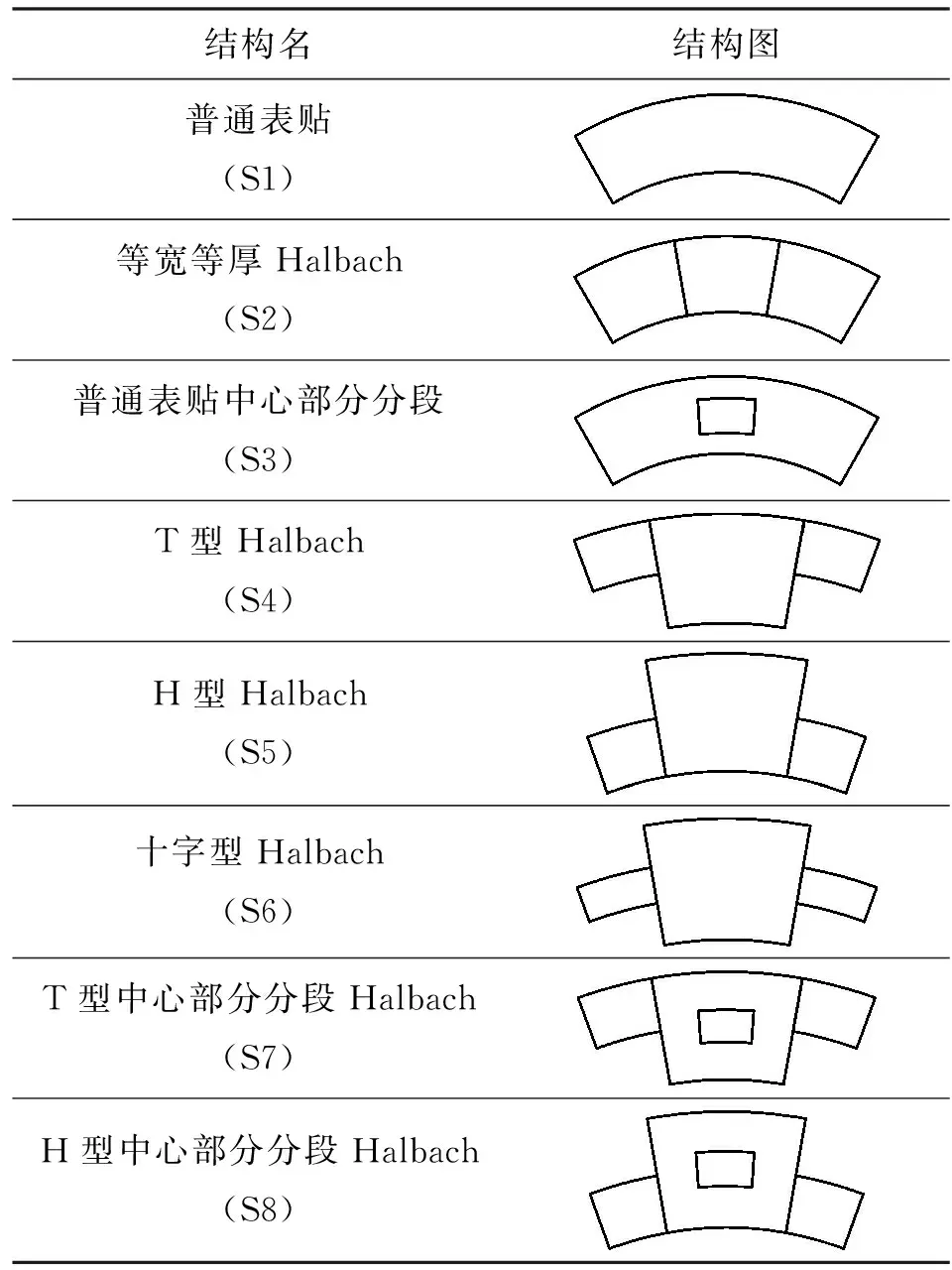
表6 8种永磁体结构

4.1 空载磁场分析

空载条件下,齿槽转矩是判断电机特性的一个重要依据。将各电机模型运动速度设置为2(°)/s得图12所示4种磁极结构PMSM的齿槽转矩对比图。

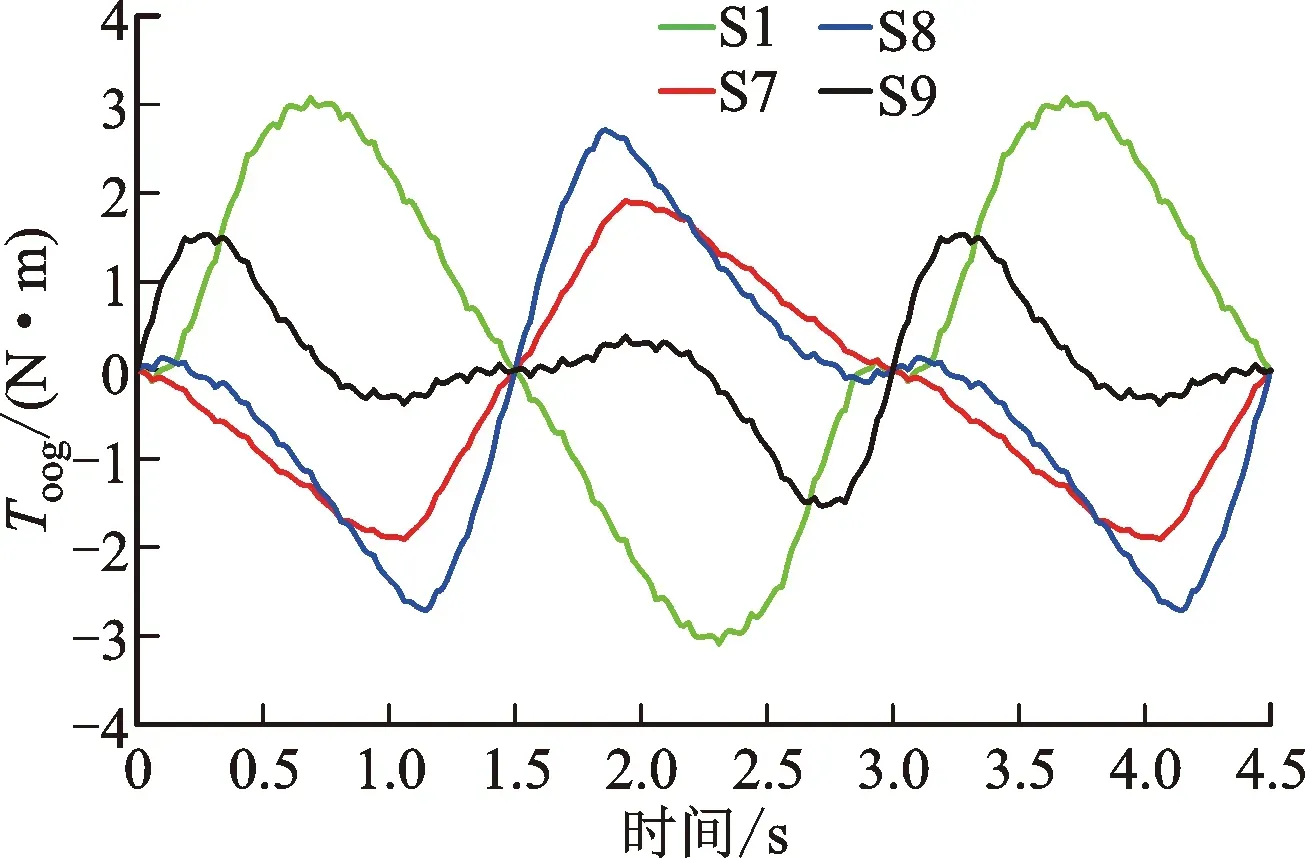
图12 齿槽转矩对比图Fig.12 Comparison diagram of cogging torque

观察图12波形可知,十字型主磁极中心部分分段Halbach磁极结构(S9)齿槽转矩峰峰值最小,为3.06 N·m。主磁极采取中心部分分段结构的齿槽转矩要比未分段磁极结构小,且十字型主磁极中心部分分段结构(S9)PMSM的齿槽转矩峰峰值最小。

4.2 负载磁场分析

图13和图14所示分别为最优T型主磁极中心部分分段、H型主磁极中心部分分段及十字型主磁极中心部分分段PMSM和普通表贴式PMSM的电磁转矩和涡流损耗的对比图。

图13 电磁转矩对比图Fig.13 A comparison diagram of electromagnetic torques

分析图13所示波形数据,经计算得到普通表贴式结构的电磁转矩为43.43 N·m,转矩脉动为11.09%;T型主磁极中心部分分段PMSM的电磁转矩为40.28 N·m,转矩脉动为12.85%;H型中心部分分段结构的电磁转矩为41.43 N·m,转矩脉动为7.35%;十字型主磁极中心部分分段结构的电磁转矩为40.96 N·m,转矩脉动为10.36%。与普通表贴式结构相比,T型主磁极中心部分分段、H型主磁极中心部分分段以及十字型主磁极中心部分分段结构使电磁转矩降低了7.25%、4.61%和5.69%,转矩脉动降低了15.87%、33.72%和6.58%。综合考察得出,H型主磁极中心部分分段结构对转矩脉动的抑制效果最好,T型主磁极中心部分分段结构最差。观察图14所示波形可以看出,十字型主磁极中心部分分段结构(S9)对涡流损耗的抑制效果最明显。

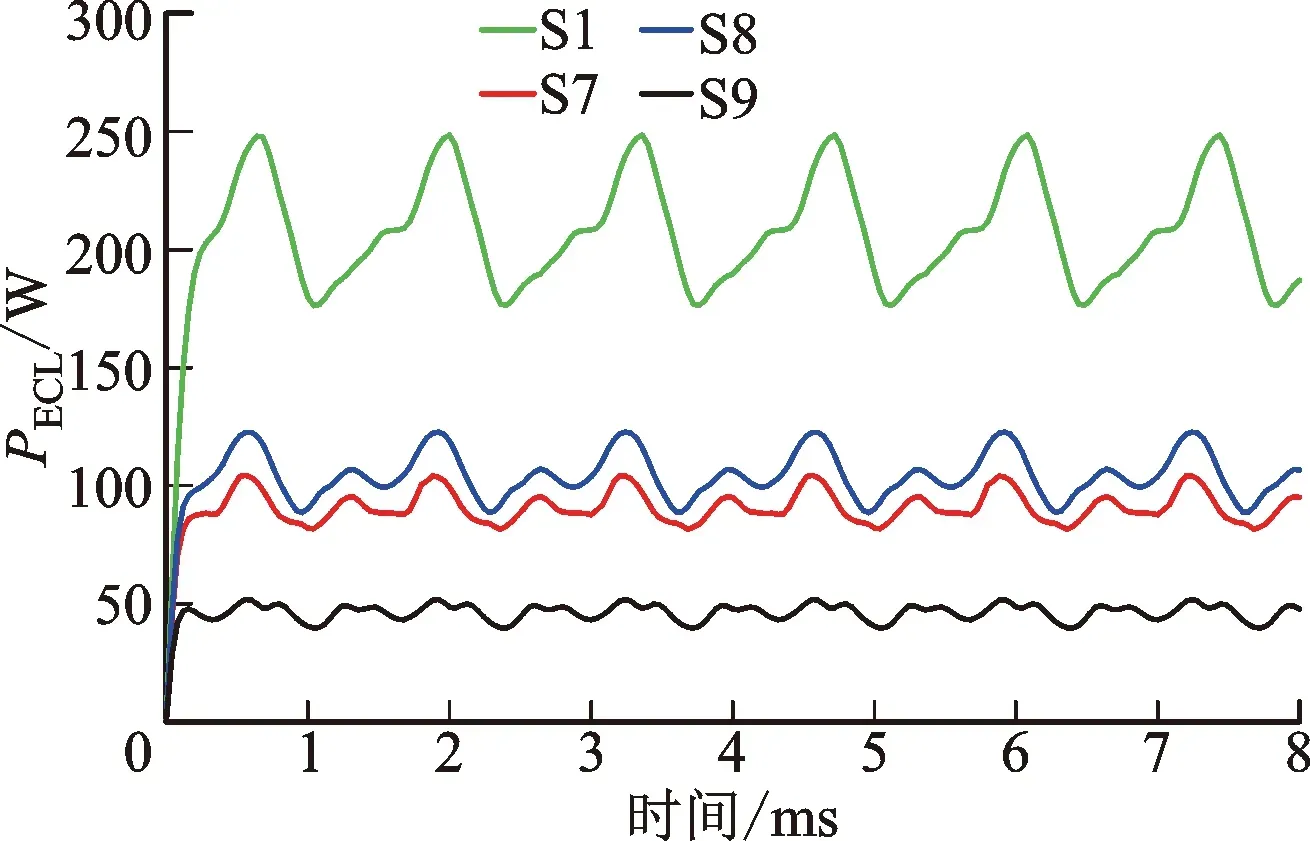
图14 负载涡流损耗对比图Fig.14 A comparison diagram of load eddy current losses

将9种磁极结构PMSM经分级多变量多目标优化算法优化至最优,综合考察表7所示9种结构的各项指标。相比于平行充磁方式下的普通表贴式结构,采用Halbach充磁方式的其他8种磁极结构PMSM均能不同程度降低气隙磁密谐波畸变率,说明永磁体采用Halbach充磁方式能有效降低电机气隙磁场谐波含量,提高机电能量转换效率。相比于普通表贴式结构,T型主磁极中心部分分段(S7)、H型主磁极中心部分分段(S8)以及十字型主磁极中心部分分段(S9)磁极结构使单位永磁体体积产生涡流损耗分别降低了44.44%、44.2%和81.45%,说明主磁极部分分段可以大幅度降低涡流损耗。对T型(S4)、H型(S5)以及十字型(S6)磁极结构进行主磁极中心部分分段后,涡流损耗大幅度降低,转矩脉动小幅度增大,但降低了齿槽转矩峰峰值且单位永磁体体积产生电磁转矩有小幅度提升,说明主磁极中心部分分段结构能在保证电机输出特性稳定的情况下有效降低涡流损耗和齿槽转矩幅值。在轮毂电机的背景下,综合考虑各项指标,H型主磁极中心部分分段Halbach结构(S8)PMSM性能最优,相比于普通表贴式PMSM,Halbach结构单位永磁体体积产生电磁转矩提高了24.46%,转矩脉动降低了33.72%,且边界磁极附着在转子表面,制作工艺简单,永磁体用量较小节省成本,具有实际应用价值。

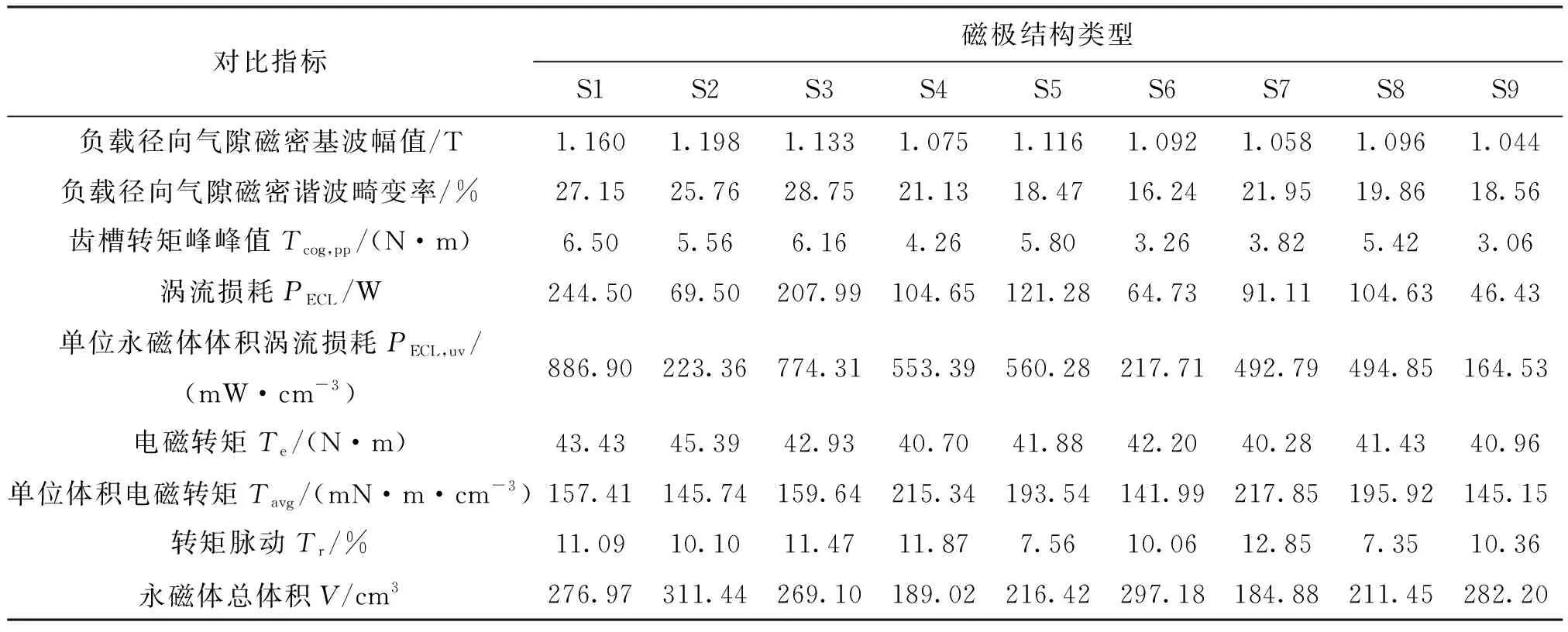
表7 优化后9种电机磁极结构指标对比

5 结 论

(1)本文提出的分级多变量多目标优化思想,与传统单参优化相比,能根据不同等级的优化结果选择不同的优化目标,确定该等级下的最优参数组合,提高了优化效率与精度。

(2)十字型主磁极中心部分分段Halbach PMSM的涡流损耗最小,与普通表贴式PMSM相比降低了81.45%,能有效抑制转子温升,有利于电机过载运行。

(3)H型主磁极中心部分分段Halbach PMSM的转矩脉动最小,较普通表贴式PMSM降低了33.72%,单位永磁体体积产生电磁转矩比普通表贴式结构高了24.46%,能有效降低轮毂电机的振动和噪声,提高机车稳定运行能力。

本文所优化的永磁体结构均为径向瓦片式结构的延伸,对降低涡流损耗效果显著,但对转矩脉动的抑制有一定局限性。在接下来的研究中考虑将永磁体两侧边线参数建模为倾斜角度可变结构,来进一步抑制转矩脉动。