精密镗床进给轴差异化主动冷却方法

赵亮,王孟超,雷默涵,任宏迪,张鑫,杨军,梅雪松

(1.西安交通大学机械工程学院,710049,西安;2.西安理工大学机械与精密仪器工程学院,710048,西安)

大量研究显示,机床由于热变形引起的加工制造误差占机床总误差的40%～70%[1-2],机床热误差问题已经成为影响我国精密机床发展的关键因素。轴承、电机和丝杠螺母副的生热传导至丝杠、立柱,直接或间接地引起丝杠、光栅尺的热变形,是进给轴产生热误差的主要原因。建立循环冷却系统带走发热部件累积的热量,是控制热误差的有效方式,已经成为解决机床热误差问题的重要途径。

针对机床生热问题,许多研究者分析了机床关键部件的生热机理,其中Li等研究了高速立式加工中心滚珠丝杠进给系统的热变形机理[3];Liu等分析了热-结构相互作用机理,提出了一种新的接触热阻计算方法,使热边界条件更完善[4];Ma等探讨了生热、散热、热应力、温升、热膨胀及由此产生的热误差等因素之间的关系,建立了两端固定进给轴的热误差模型[5];Hu等建立了热误差和轴向伸长之间的关系来表征热误差分布[6];Arne等分析了超精密进给轴在不同定值速度下的定位行为,并与高速进给轴进行了比较[7];Zhang等学者推导了运动关节的等效轴向刚度和传动刚度,分析了系统动态特性随加速度的变化规律[8];Min等分析了丝杠螺母副的发热、轴承与轴承座的热传导、丝杠与环境的热对流等的影响[9];王大伟等研究了滚珠丝杠传动过程中温度场的分布规律和温度与丝杠变形间的关系[10]。以上针对机床生热机理的研究为热误差的预测和控制提供了研究基础与理论支撑。

同时,很多学者通过仿真和数学建模等手段对机床热误差进行了模拟与预测。Kim等研究了进给系统定位误差的机理,并采用有限元法分析了进给系统热特性和热误差[11];Xu等基于有限元分析和改进的集总热容法建立了丝杠的热特性模型,并给出了轴承、丝杠螺母副的发热和散热方程[12];Guan等对行星滚子丝杠机构在不同工况下的热特性进行了分析和实验研究,建立了一个基于热网络法的热模型来预测热特性[13];Jia等将进给轴热误差表述为多项式函数的乘积,提出了基于齐次变换的热误差补偿方法[14];马驰等基于接触角迭代法计算滚动轴承的生热功率,并引入分形理论和蒙特卡罗法计算了结合面间的接触热导[15];杨军利用模糊聚类方法对温度测点进行了优化,建立了主轴轴向热伸长及径向热倾角的综合热误差模型[16];Lei等针对进给轴热误差提出了一种基于联合训练和支持向量回归的半监督建模方法[17];Hui等从理论上分析了光栅标尺的热膨胀和工件的热变形,提出了定位误差和工件变形误差的数学模型[18]。以上研究通过建模仿真或建立数学模型来预测机床热误差情况,再通过机床控制系统进行相应控制以减小热误差,但是存在仿真预测精度有限以及数学模型泛化性不强的缺点。

对于机床外加热误差控制设备的研究,Shi等研究了进给传动系统螺杆轴的温度分布与冷却系统参数及冷却介质流量的关系[19];Immanuel等设计了一种基于相变材料的潜热储存装置,并研究了基于热阻网络来评估滚珠丝杠性能的方法[20];Ge等提出了一种利用碳纤维增强塑料的热收缩来抑制热误差的方法[21];Teng等提出了一种基于功率匹配的热误差冷却策略[22]。这些方法对于减小热误差均有一定的效果,但都需要较大程度地改变机床本体结构且安装较为复杂。

综上,目前针对进给轴的研究,多集中于热误差的分析、建模、冷却液参数对进给系统热特性的影响,少有针对进给轴热误差控制方法的研究,且也多以恒温控制为主。本文以双驱滚珠丝杠X进给轴为研究对象,探索了机床内热源的生热和传热机理,并通过仿真研究了主动冷却对于热误差的影响。在冷却方案的可行性得到初步验证后,设计了进给轴的主动冷却系统并对冷却策略进行了研究。最后,针对进给轴,提出一种根据生热率计算实时控制冷却板进出口温度的多回路差异化主动冷却方法,从而能够精确地带走合适的热量,减少热误差,缩短热误差稳定时间。

1 精密镗床进给轴主动冷却方案及仿真分析

1.1 进给轴主动冷却方案

对于进给轴,内部热源包括轴承、电机和丝杠螺母副,它的产生的热传导至丝杠、立柱,最终引起光栅尺和滚珠丝杠的热变形,是进给轴产生热误差的主要原因。基于冷却循环方式带走热源生热是一种有效的热误差控制手段,拟在靠近热源的位置布置冷却器,冷却液流经冷却器,带走一部分热量从而减少热量的聚集,以改善机床的温度场和变形场。进给轴的冷却器选用冷却板,固定在进给轴各个热源的位置。

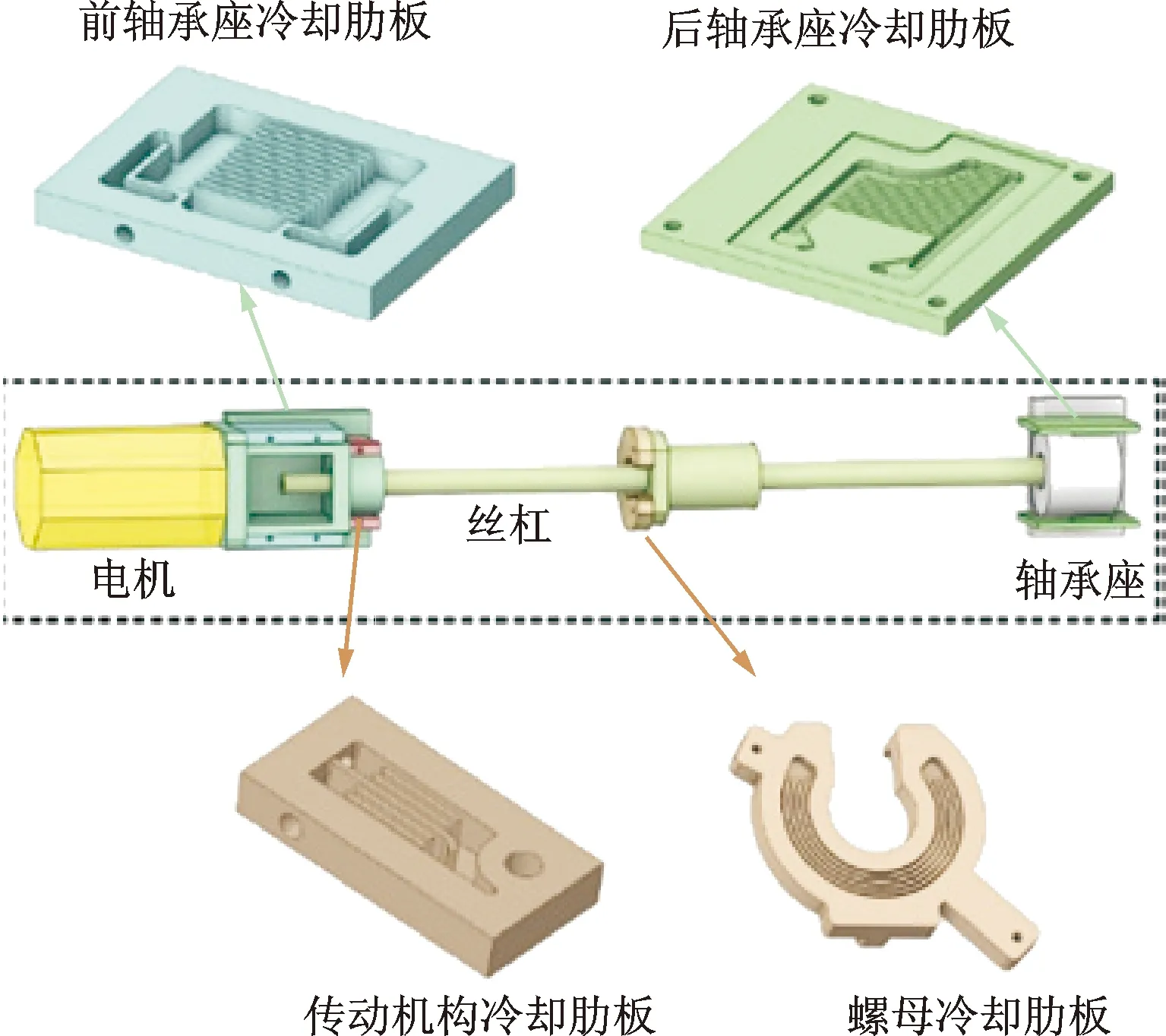
图1 双驱X进给轴冷却板分布图 Fig.1 Distribution diagram of dual-drived X-feed shaft cooling plate

进给轴差异化冷却的对象是精密镗床发热量较大的双驱滚珠丝杠X进给轴,冷却主要包括空心丝杠的自带冷却和4种自主设计的冷却器,冷却器采用导热性能好的材料,安装部位分别为电机前轴承处、丝杠螺母处、后轴承处以及传动机构处,图1为进给轴冷却板的安装实物和示意图。上丝杠的冷却板有前轴承座2处、后轴承座2处、传动机构处2处,共6处;下丝杠冷却板除了和上丝杠一样的冷却板外,还有丝杠螺母副1处,共7处。冷却板通过螺栓连接牢固地安装在进给轴相应的冷却部位。冷却器内部流道呈U形和W形,截面形式分圆形和矩形,其内部设计有一定距离间隔的分流片来加强换热。一定温度和流量的冷却液从冷却板的进水口流入,流经内部流道后从出水口流出,带走相应位置的热量,实现对相应部位的冷却。

每个冷却板由背板和槽道板构成,为增强换热效率,槽道板上通过设计不同长度和数量的翅片从而形成不同的流道形状,大致分为Y型和U型,冷却液的入口和出口均根据安装位置的实际需要灵活布置。4种冷却板的形状参数设计见表1。

表1 冷却板形状参数

1.2 进给轴热边界条件计算

对于生热,进给轴热源主要有电机、轴承、丝杠螺母副;对于热传导,重新设置靠近热源的关键部位接触热阻,包括轴承和轴套、冷却板和镗床外壳间接触热阻。热对流的边界条件是对流换热系数,进给轴旋转部件与空气的强迫对流换热系数和静止部件与空气的自然对流换热系数分开设置。

1.2.1 主要热源生热 轴承的生热主要由摩擦引起,轴承的生热可以通过功率损失间接得到,也可以用整体法和局部法计算得到,本文拟采用基于Palmgren经验公式并考虑滚动体自旋摩擦生热的计算方法得到轴承的生热率。Palmgren通过大量实验,推导了滚动轴承包含整体载荷摩擦力矩和黏性摩擦力矩的经验公式[23]

M1=Mf0+Mf1

(1)

式中:M1为滚动轴承摩擦力矩,N·m;Mf0为滚动轴承黏性摩擦力矩,N·m;Mf1为滚动轴承整体载荷摩擦力矩,N·m。Mf0与润滑剂的黏度和轴承的转速有关

(2)

式中:f0为常数,与轴承结构和润滑方式有关;νb为滚动轴承润滑剂运动黏度,m2/s;nb为滚动轴承内圈转速,r/min;db为轴承节圆直径,m。

润滑剂的运动黏度νb受温度影响较大,其与温度的关系如下

νb=νr0e-b(Tb-Tb0)

(3)

式中:νr0是润滑剂初始运动黏度,m2/s;b为经验常数,取0.024 2;Tb为轴承温度, ℃,经验估计;Tb0为轴承初始温度, ℃,认为是环境温度。

整体载荷摩擦力矩Mf1的计算公式如下

(4)

式中:f1、c是常数,与轴承结构和润滑方式有关;Fs是当量静载荷,N,由轴向载荷和径向载荷线性叠加;Cs是额定静载荷,N;Fba是轴向载荷,N;αb是球轴承接触角,rad;Fbr为径向载荷,N。

通过手册查询,双列角接触球轴承油脂润滑对应的常数f0、f1、c分别为1.5～4、0.002、0.33。球形滚动体与内外圈滚道之间的自旋摩擦也是轴承生热的重要原因,内外圈接触器自旋摩擦力矩Msie可使用下式计算

(5)

式中:κsie是滚动体与内、外圈沟道接触摩擦系数;Fie是滚动体与内、外圈沟道的法向载荷,N;aie为内、外沟道赫兹接触椭圆长半轴,m;εie为内、外沟道接触第二类椭圆积分。

轴承内、外圈因自旋摩擦的总生热率为

Qi,e=zbωsieMsie

(6)

式中:Qi,e是轴承内、外圈沟道接触区的生热率,W;zb是球数量;ωsie为滚动体自旋角速度,rad/s。

轴承总的生热率为

Q=M1ω+Qi,e

(7)

式中:Q是轴承总生热率;ω为轴承角速度,rad/s。

式(5)、(6)计算中,内外圈的轴承对应的自旋角速度ωsie以及法向载荷Fie采用拟静力学法求解。

电机损耗生热有铜耗、铁耗及附加损耗,在电机内部结构及材料无法有效得到的情况下,从电机的生热传热机理入手建立生热数学模型计算生热率是困难的,考虑从能量损耗的角度,利用电机已有参数间接求得,电机的生热功率Qmotor计算公式为

(8)

式中:Pm为电机功率,W;ηm为电机效率;Mm是电机输出力矩,N·m;nm为电机转速,r/min进给系统的传动单位包括丝杠螺母副以及导轨滑块副,经实验研究以及数值计算,导轨滑块的摩擦生热量较小,可忽略不计,进给轴中丝杠螺母副的生热与丝杠转速和摩擦力矩密切相关,其生热功率Qnut为

Qnut=CnutMnutnnut

(9)

式中:Cnut是常数,取0.102 9;nnut为丝杠转速,r/min;Mnut是滚珠丝杠的摩擦力矩,N·m,可近似为驱动力矩和阻力矩线性叠加[23]

Mnut=0.94MP+MD

(10)

式中:MP为阻力矩,N·m;MD是驱动力矩,N·m。阻力矩和驱动力矩的计算公式如下

(11)

式中:Fsa为轴向载荷,N;Ph是丝杠导程,这里为20 mm;ηnut为丝杠螺母副传动效率;FP是轴向预紧力矩,N·m。

1.2.2 对流换热系数计算 仿真主要考虑了空气分别与进给轴系统静止表面和旋转表面、以及冷却液与冷却器的对流换热系数。换热系数h可以经验地表示为

(12)

式中:Nu是努塞尔数;λ为空气/冷却液导热系数,W/(m· ℃);L是特征尺寸,m。

从该经验公式中,可以发现对于一定情形,特征尺寸和传热系数是相对容易得到的,关键是如何确定几种情形下的努塞尔数,因此需要分开讨论。

丝杠旋转外表面与空气对应的努塞尔数Nu可表示为

(13)

其中

(14)

式中:ωa是进给轴旋转角速度,rad/s;da为进给轴当量直径,m。

进给系统的静止表面与空气发生自然对流换热,努塞尔数Nu可表示为[23]

Nu=f(GrPr)n

(15)

式中:f、n均与空气的流动状态和换热面的几何形状有关。

对于进给轴的冷却板内冷却液的流动,其努塞尔数根据冷却液流动状态各有不同,计算公式为

(16)

式中:Pre为机床表面温度下的普朗特数;K为校正系数。

1.2.3 冷却板硅脂镗床外壳结合面热阻 进给系统中的冷却板通过螺栓连接进行压紧固定,施加的外部压力Fn可表示为

(17)

式中:Tn是拧紧力矩,N·mm;dn为螺母的公称直径,mm;Kn是螺栓拧紧力矩系数。

对于公称直径dn为4 mm的螺母,施加在扳手上的拧紧力矩Tn一般在在3～5 kN·mm之间,本文取值为4 kN·mm;对于无润滑的干燥连接表面,Kn取值0.26。算得外部压力Fn≈385 N,忽略冷却板的弹性变形,法向压强Pn≈616 kPa。当硅脂-金属结合面间法向接触压力>20 kPa时,结合面间的导热硅脂厚度σb为

(18)

式中:C、m是常数,C=1.31×10-4,m=0.166;τ0为导热硅脂的屈服应力,τ0=36.18 N/m。

进给系统相关部位的材料为HT300,表面粗糙度约为3 μm,冷却板材料为2A12铝合金,表面粗糙度约为2 μm。通过共聚焦显微镜获取2A12铝合金的表面形貌相关数据,最终算得冷却板-硅脂-进给系统结合面的总热阻Rall为5.815×10-4m2/ (℃·W)。

1.3 精密镗床热流固耦合仿真

精密镗床热-流-固耦合仿真流程见图2,主动冷却下的进给轴的热-流-固耦合仿真在Ansys Workbench中进行,首先建立工程,将主动冷却的镗床的三维结构导入Geometry中,在Fluent中对流体域相关参数进行设置,得到在一定冷却条件下冷却器的温度场和变形场;将结果导入Thermal和Structural中,对热源、热阻、对流系数等边界条件设置后进行仿真,同时,考虑了结构体对流体域的影响,及镗床系统对冷却液的影响,使用System Coupling模块将上述3个模块进行耦合,最终得到镗床系统的瞬态温度场和瞬态变形场。

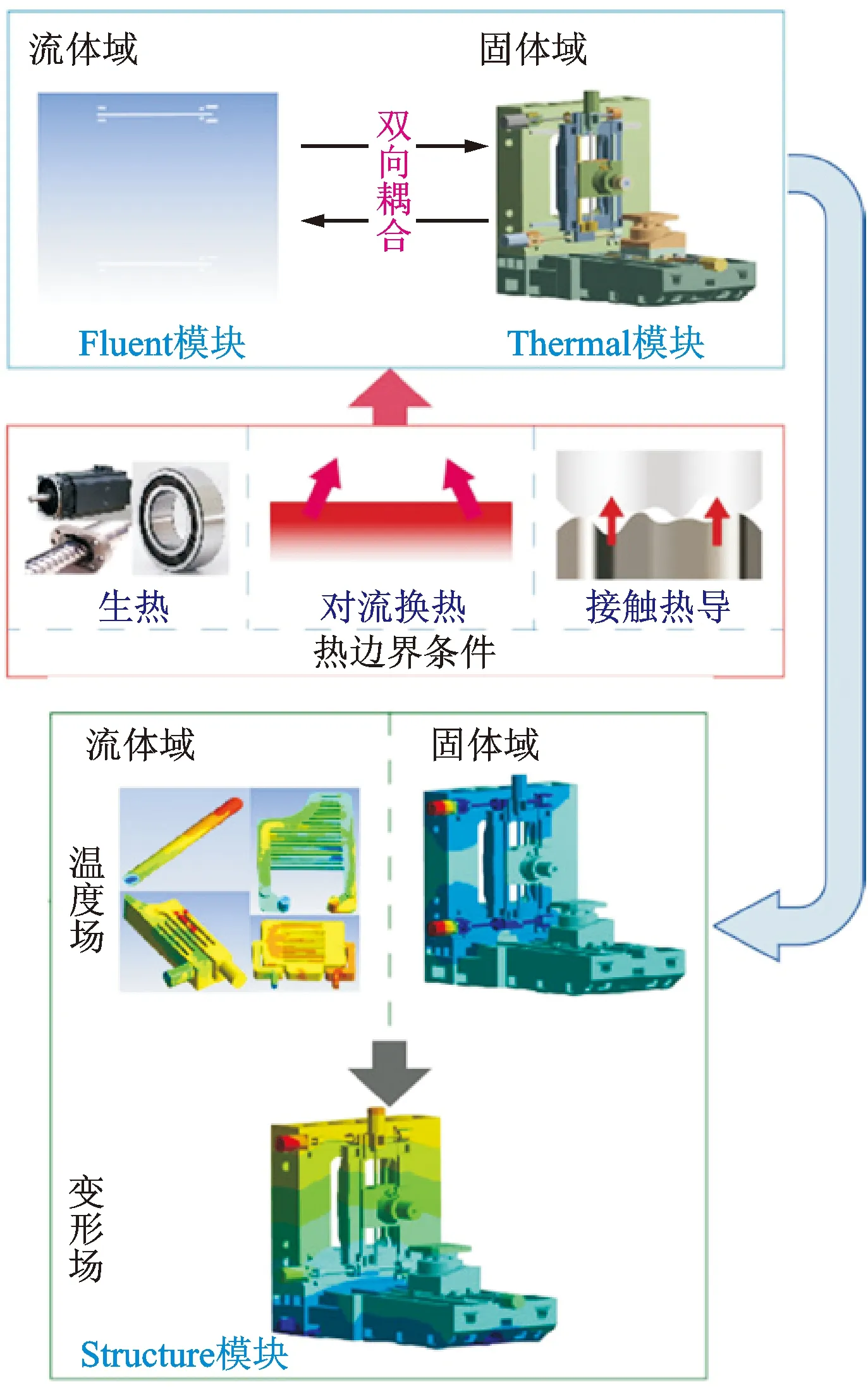
图2 主动冷却的精密镗床热-流-固耦合仿真流程Fig.2 Thermal-fluid-solid coupling simulation process of precision boring machine with active cooling

仿真流程大致为:建立三维模型,导入Ansys软件划分网格,添加材料属性,进行边界条件计算以及仿真设置,最终得到精密镗床的温度和变形场。

为了对进给轴基于冷却板的主动冷却方案进行验证,需要对进给轴进行仿真,在建模的过程中需要做一些必要的简化,简化后的三维模型如图3所示。

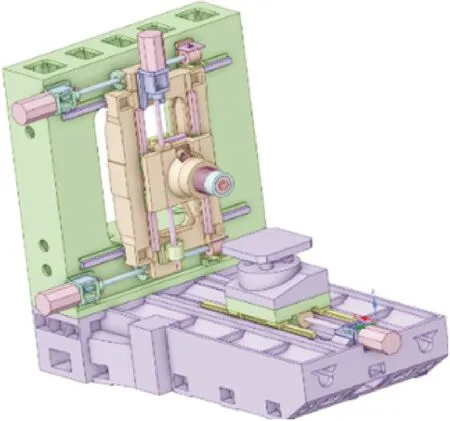
图3 精密镗床三维模型Fig.3 3D model of precision boring machine

本研究网格包括流体仿真中的流道网格,以及热固耦合中的实体网格。流道网格采用DM抽取,实体网格使用Workbench内置网格划分功能。本次研究中流道网格节点数为254 337,网格数为195 315。用于流固计算的网格共有911 497个节点、513 637个网格。仿真边界条件如表2所示。

表2 进给轴热边界条件

镗床进给轴进给速度为5 m/min,冷却液温度为18 ℃时的仿真结果如图4所示,由图可知温度主要集中在电机附近,最大热变形达到97 μm。图5为进给轴有无冷却热误差对比图,可看出在冷却流道的作用下,进给轴热误差有效减小,远离电机端定位误差下降最多,降低5 μm左右,初步验证进给轴的冷却方案可以对各热源热量进行有效散热以及控制热量扩散至传动机构。

(a)仿真温度云图

图5 进给轴有冷却和无冷却对比图Fig.5 A comparison chart of feed axis with and without cooling

2 精密镗床进给轴主动冷却系统设计

2.1 精密镗床主动外冷却系统

硬件上,多回路差异化的进给轴主动冷却系统由冷却循环回路、工控机、PLC控制模块、冷却器和冷却油箱组成,冷却系统原理如图6所示。冷却液使用4号主轴油,共使用7路冷却回路,其中前轴承座和传动构件的冷却器共用1路,空心丝杠、后轴承座、丝杠螺母副处各用1路。

图6 进给轴多回路差异化冷却循环系统示意图Fig.6 Schematic diagram of multi-circuit differentiated cooling circulation system of feed axis

进给轴主动冷却系统的冷却回路结构如图7所示,每条冷却回路由工控机模块、PLC模块以及温控循环模块组成。工控机模块主要为软件控制部分;PLC模块是连接工控机模块与温控循环模块的桥梁;温控循环系统主要包括温控箱、循环油泵、压力计、调节阀、流量计、温度/压力传感器与外置冷却器等,是控制冷却液流动状态的执行器。

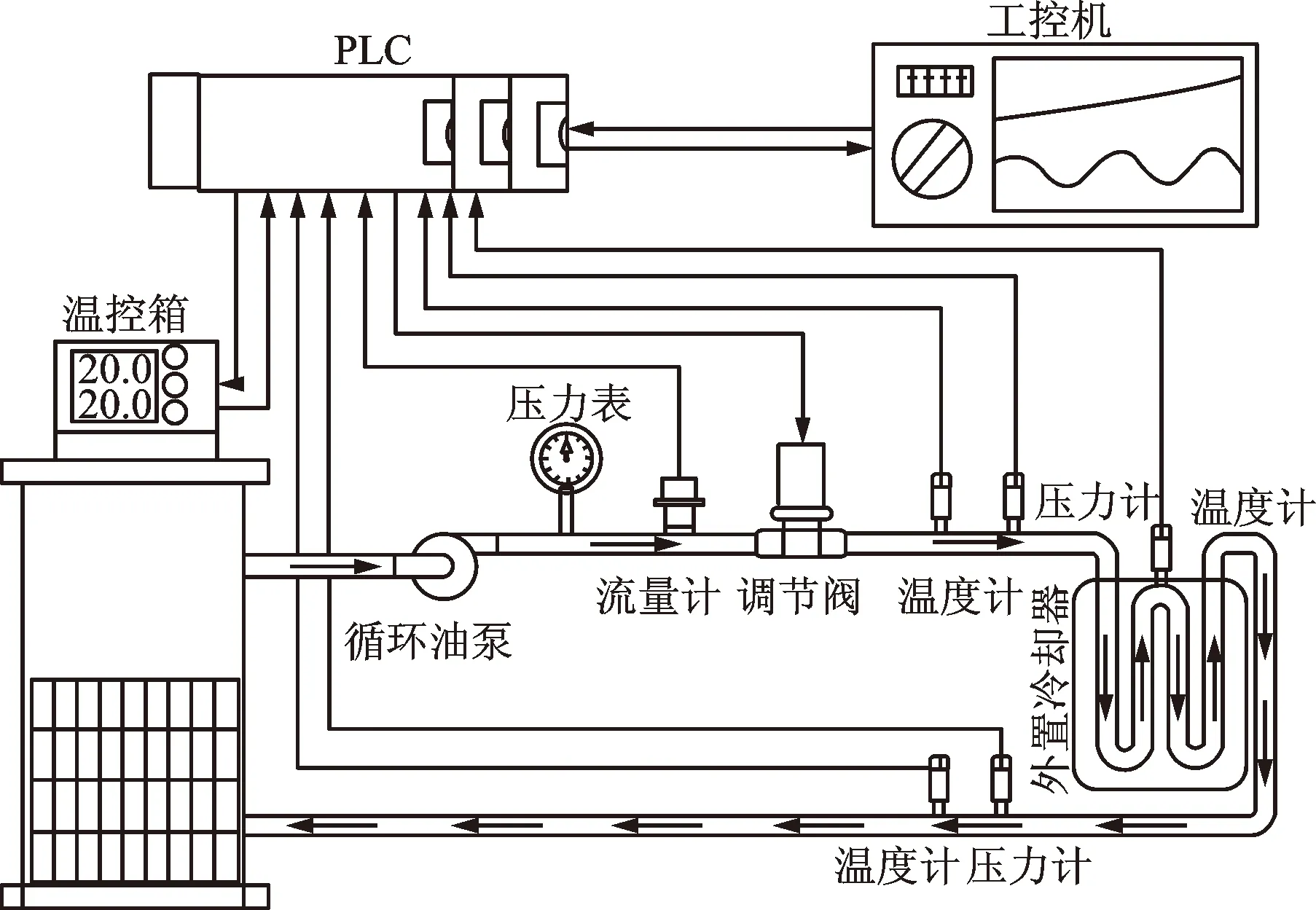
图7 进给轴主动冷却系统冷却回路结构图Fig.7 The structure of the cooling circuit of the feed axis active cooling system

冷却循环回路的冷却液从冷却油箱出发,通过循环油泵增压,依次经过压力表、流量计、比例调节阀、进口温度计、压力计,进入到冷却器,在冷却器中与热源进行换热后,依次通过出口温度计、压力计回到冷却油箱;PLC控制模块负责采集循环回路上的传感器数据,同时与冷却油箱、工控机进行数据交互;冷却油箱作为油箱调节的执行机构,根据输入的油温指令通过内部的PID控制器控制内部的电热棒和压缩机动作来调温;工控机作为上位机,是控制和显示终端,在这里进行整个系统数据的读取、存储、写入,运行控制算法。

2.2 进给轴差异化冷却仿真与实验分析

无冷却和恒温冷却进给轴的实验和仿真对比结果见图8。图8可以看到,进给轴仿真在个别点处发生一定的偏离,但可以准确地描述进给轴热误差的变化趋势,测点最大偏移量不超过2 μm。热误差的变化具有一定的规律性:越是远离电机端的测点,产生的热误差变化就越大;随着时间的进行,定位误差的变化率下降,趋于稳定。

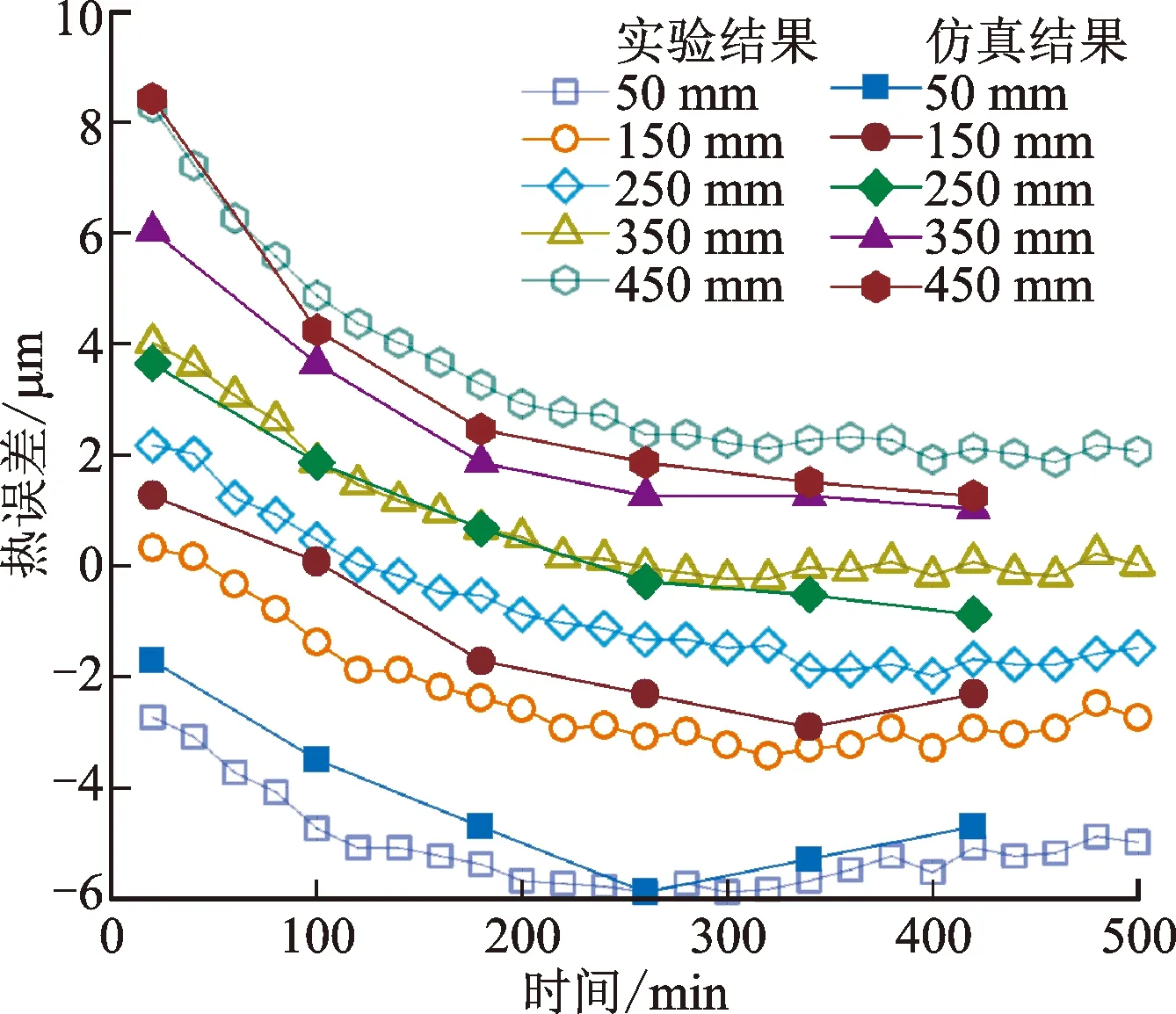
(a)恒温冷却仿真与实验结果对比

3 进给轴多回路差异化温度控制

3.1 进给轴的多回路差异化温度控制策略

进给轴热误差是机床热误差的重要组成部分[24],进给轴的关键部位热源包括伺服电机、轴承、丝杠螺母等,它们会产生大量热,使得丝杠、床身发生热变形[25]。虽然采用光栅尺反馈的闭环伺服控制系统可以补偿部分误差,但是上述热变形将不可避免地引起光栅尺的变形,从而产生热误差。本节以双驱丝杠X进给轴为研究对象,计算一定进给速度下的轴承、电机和丝杠螺母副热源的生热率;根据生热率得到进出口温差的目标控制值,并采用PID算法对温差进行控制,并进行了无冷却、恒温冷却和差异化温度控制策略的实验。

光栅尺的伸长和弯曲是滚珠丝杠进给轴产生直线定位误差的主要原因,采用丝杠中空冷却的方式可以带走大部分热量,但是过度冷却和仅丝杠冷却会使得冷却不均匀,从而导致热变形,并造成进给轴的直线定位误差。对进给轴多热源进行差异化冷却,从而恰当带走热源产生的热量,以有效减少进给轴热误差。

进给轴差异化冷却的控制目标为冷却器的进出口温度差ΔT,该物理量可以表征冷却液带走的热量,主要由散热部位的生热率和热耗散系数来决定。进出口温度差的表达式为

(19)

式中:c=1 851 J/(kg·℃)为冷却液比热容;ρ=871 kg/m3为冷却液密度;Q=0.1 L/s为冷却液流量;Hg为生热部位生热率;kH为热耗散系数。生热率由第2节中的公式计算,kH由实验优化,经验选择kH=5.5。

计算温度控制目标的关键在于热源的生热率计算,对于X进给轴运动,生热部件主要为轴承、电机、丝杠螺母副,它们的生热率已在前文中给出。在实验中,除了测量时采用较低的进给速度外,进给轴连续往返运行的进给速度均为5 m/min,最终得到各热源的生热率和进出口温度控制目标值,计算结果见表3。

表3 X进给轴各热源生热率及进出口温差目标控制值

3.2 进给轴多回路差异化冷却实验

在确定轴承座、电机等4处关键热源部件冷却回路中的控制输入后,在环境温度和机床初始温度为19.5 ℃左右的状态下,针对精密镗床中的双驱滚珠丝杠X进给轴进行差异化冷却实验(冷却液密度、流量等实验参数选取图3.1节参数值),与无冷却实验进行实验对比,实验结果如图9所示。

(a)无冷却X进给轴实验

图9a为无冷却双驱X进给轴实验,由图可见每个点的热误差随着时间的推移及与电机距离的增大呈升高的趋势,初始热误差为0,随着实验进行,可见离电机距离越远,热误差变化越大,从而形成一种远端“翘起”的结果,这是由于近端的热误差变化会影响远端。在最远端趋于稳定时的热误差最大,最远端500 mm处的热误差一直增大至13.03 μm,最近端50 mm处为7.21 μm;同时每个点的热误差慢慢增加至趋于平稳。对单个点而言,变化速率越来越小;对不同点的热误差进行比较,离电机越远,变化速率越大,最终达到的热误差越大。

图9b的曲线变化规律与前两组实验不同:在位置尺度上,可以看到前200 min,各个坐标点的热误差几乎等幅增大,200 min以后曲线才渐渐地呈现远端热误差值大于近端的倾斜情况,最大的热误差仍为最远端500 mm处,值为5.4 μm,最近端的热误差为1.7 μm;时间尺度上,热误差曲线规律呈现了很大的不同,首先在开始的200 min内,热误差几乎等幅增大,在之后的时间里,靠近近端(50、100、150、200 mm)的热误差呈现上下波动的效果,中端(250、300、350 mm)的热误差保持平稳,远端(400、450、500 mm)的热误差变化缓慢增大达到平稳。

通过几组实验对比分析,无冷却和差异化冷却的远端500 mm最大的热误差分别为13.03和5.04 μm,相对于无冷却实验最大热误差下降了58.56%,近端50 mm最大的热误差分别为7.21 μm、1.7 μm,相对于无冷却实验最大热误差下降了76.42%,热误差趋于稳定时间依次缩短。采用18 ℃恒温冷却方法时进给轴最大热误差为8.25 μm,采用差异化冷却时进给轴最大热误差为5.4 μm,相比恒温冷却方法下降了34.55%。

综上,差异化冷却控制策略相比于无冷却和恒温冷却方法可以有效减小热误差,缩短热误差稳定时间。

4 结 论

本文以双驱X进给轴为研究对象,提出精密镗床进给轴主动冷却方案,并建立热流固耦合仿真模型进行验证,在此基础上搭建了双驱X进给轴冷却循环系统,并提出了主动冷却下的进给轴热误差控制策略,最后通过实验进行验证,得到如下结论。

(1)为了控制精密镗床热误差,提出了进给轴主动冷却方案,分析了热源生热和散热机理,对关键边界条件进行计算,建立起主动冷却下的热流固耦合仿真,对基于多热源散热板的进给轴分别进行了有无冷却的仿真,仿真结果表明有冷却下,热误差有效降低,初步验证了所提出主动冷却方案的有效性。

(2)针对进给轴多回路主动冷却系统,提出了一种基于温度控制的多回路差异化冷却方法。以双驱X进给轴为实验对象,控制各个热源部分冷却液的进出口温度以精确地带走合适的热量,以最小化立柱、光栅尺的热变形。采用差异化冷却控制策略与无冷却进行实验对比,最大热误差下降了58.56%以上,同时热误差的稳定时间亦小于后者;与恒温冷却方法相比,最大热误差下降了34.55%。热误差相对稳定后,调整工件与机床坐标系的相对位置可以事前平衡掉热误差中的稳定部分,使残留热误差维持在较小的波动范围,对提升机床末端加工精度具有重要意义。