对二甲苯悬浮结晶与晶体流动分布特性研究

董佳宇,任智宏,彭小成,陈强,王斯民

(1.西安交通大学化学工程与技术学院,710049,西安;2.中石化广州工程有限公司,510620,广州;3.中国石化炼化工程集团洛阳技术研发中心,471003,河南洛阳)

符号表

高纯度对二甲苯是化工行业应用极广的有机材料[1-3],一般由芳烃联合装置工业化生产[4]。由于对二甲苯与其同分异构体间沸点差异很小,因此采用精馏技术分离对二甲苯难度较大[5],但其冰点比其他碳八芳烃高很多,目前工业上主要利用这一性质通过熔融结晶法实现对二甲苯的分离[6-7]。

熔融结晶技术效率高、能量消耗低、绿色环保[8],但其本身包含传质、相变等复杂过程,不同环境与操作条件极易影响产品的质量及产能[9]。大量学者研究了操作参数、结晶器样式等对晶体产品的影响,尝试对对二甲苯结晶生产进行研究和优化[10-13],但研究多局限于分析相关参数对最终产物的影响,没有充分研究晶体颗粒的生长、汇聚等情况。这主要是因为结晶过程较复杂且为动态过程[14],很难通过实验有效研究结晶器内部的结晶过程。近年来随着计算机科学的进一步应用,计算流体力学(CFD)技术被用来设计、控制以及最终优化结晶过程[15-18]。李昭等对某新型钾盐结晶器内的连续结晶过程进行研究,对比不同操作条件下的流场情况,得出使结晶器效益最高的搅拌速度[19]。Tizbin等采用两相欧拉-欧拉模型,结合颗粒流动力学理论,对工业强制循环结晶器进行了模拟研究,发现约65%的晶体生长发生在结晶器的沸腾区与混合区[20]。

但是目前却鲜有利用CFD技术数值模拟对二甲苯结晶的研究,因为一般所模拟的结晶过程都是从单一物质水溶液中析出溶质的过程,而对二甲苯结晶却是从混合二甲苯母液中析出对二甲苯的过程,涉及的物质组成和相间作用较为复杂。又一大区别在于,学界所研究的大部分结晶过程的结晶温度都在20～100 ℃左右,对二甲苯结晶时的系统温度在-20～0 ℃,对环境要求更苛刻,晶体在常温下极难保存,造成了实验研究的困难,因此数值模拟研究对二甲苯的结晶分离过程具有重要意义。

结晶模拟与一般多相流模拟最大的不同在于,结晶过程中颗粒相的粒径和数量都在变化,因此本文结合粒数衡算方程,关联对二甲苯结晶成核速率及生长速率方程,采用自定义函数(UDF)将对二甲苯成核、生长的动力学模型引入到粒数衡算方程中进行耦合,建立相间质量传递模型,创新性地对对二甲苯悬浮结晶行为进行直接模拟,研究晶体的生长、汇聚、流动与分布等情况,明确对二甲苯在结晶器内部的结晶与悬浮流动过程,为工业上对二甲苯的生产和优化创新提供依据与理论指导。

1 几何模型与数值方法

1.1 几何模型

结晶器选用DTB型结晶器,即晶浆内循环式结晶器[21]。图1为结晶器的物理模型,挡板位于结晶器壁面上;搅拌桨由3个45°倾斜长方形直板构成。结晶器关键位置几何尺寸见表1。

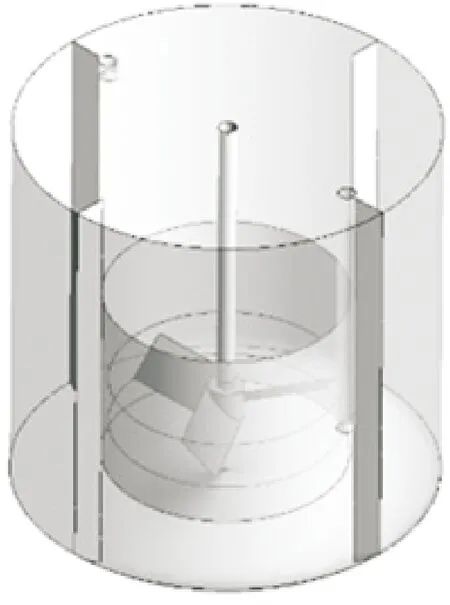
(a)结晶器三维示意图

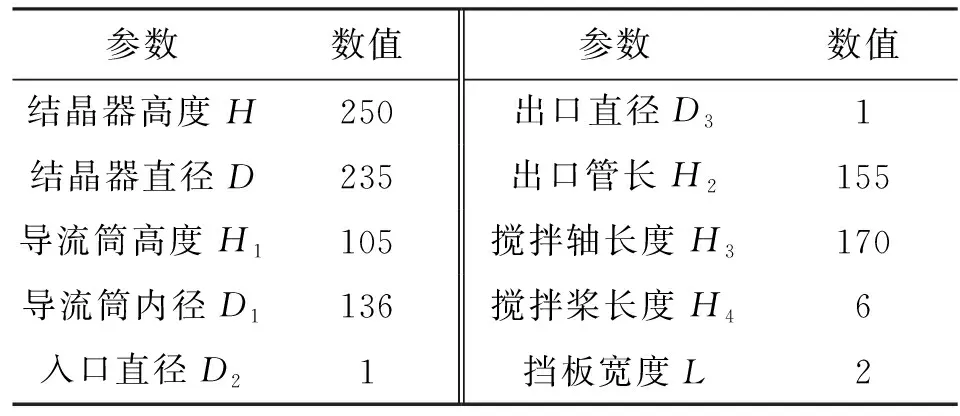
表1 模型几何尺寸

1.2 控制方程

本研究核心为固液两相流模拟,采用欧拉-欧拉模型描述晶体与流体间相互作用[22],相关方程如下。

1.2.1 第q相连续性方程

(1)

1.2.2 第q相动量方程

(Fq+Flift,q+Fvm,q)

(2)

式中:τq为第q相的应力-应变张量,计算公式为

(3)

1.2.3 第q相能量方程

(4)

式中:Qpq为相p与相q间的换热量,可假设为相间温差与相界面面积的函数,公式为

Qpq=hpqAi(Tp-Tq)

(5)

其中hpq为相间传热系数,与p相努塞尔数Nup相关。

(6)

1.2.4 守恒方程求解形式 对于n相流动,各次级相体积分数由连续性方程求解得到

(7)

1.2.5 湍流方程 由于结晶器内搅拌桨导致流场复杂,流体为完全湍流流动,因此湍流模型选取更适用于计算高雷诺数流动的标准k-ε模型,此模型也被大量应用于计算固液两相流及带有搅拌桨的流场。模型表达式如下

(8)

(9)

1.3 粒数衡算方程

由Hulburt等[23]以及Randolph等[24]提出的粒数衡算方程描述了粒子在时间和空间上的性质,可用于描述晶体粒子的粒数密度随时间、空间的变化趋势,以表征离散相体系中晶体的粒度分布及相间微观行为[25-26]。粒数衡算方程表达式为[27]

Ba-Da+Bb-Db

(10)

对二甲苯除了在外部的空间运动外,还有自身生长所引起的内部变化速率,暂不考虑晶体的聚结与破碎,可将式(10)分解为

(11)

对于粒数衡算方程,本文采用分组法进行求解,将对二甲苯晶体按照不同粒径分为有限个分散相,通过计算每个分散相与连续相及分散相间的质量、动量等的传递,得到结晶器内部的分散相分布情况。式(11)可写为以粒径为i的相体积分率计算的形式

(12)

分析式(12)可发现,粒数衡算方程的本质就是连续相的溶液与晶体相,以及不同晶体相间的传质过程[28]。将相间传质速率与对二甲苯结晶动力学进行关联,实现粒数衡算方程与连续性方程的耦合,从而对对二甲苯结晶行为进行模拟计算。

2 边界条件与模型验证

2.1 物性参数

将对二甲苯晶体按粒径设置为多个粒子组,综合考虑计算量后定义5个分散相。组分1为二甲苯母液,密度889 kg/m3,母液中对二甲苯质量分数为80%。组分2至组分6为不同粒径对二甲苯晶体,密度1 055.6 kg/m3。

对二甲苯结晶动力学模型选取陈亮等的研究成果[29],成核速率模型为

(13)

生长速率模型为

G=46.99S3.54

(14)

相对过饱和度S可由溶质质量分数与对二甲苯母液平衡浓度计算得出,其中平衡浓度公式为

-lnx=0.259 9(Tm-T)[1+0.002 8(Tm-T)]

(15)

2.2 边界条件

根据MSMPR模型并结合实际生产过程,对初始晶体的粒径及体积分数进行设置,分散相的初始参数见表2。入口速度为0.5 m/s,出口类型为压力出口,结晶温度按实际生产温度定为-20 ℃,搅拌桨的旋转利用mrf(多重参考系)模型进行模拟[30],转速设为500 r/min。

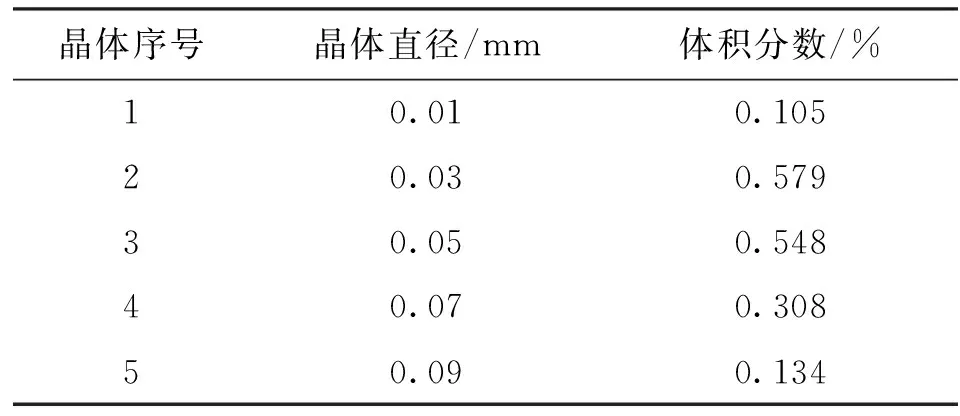
表2 分散相初始参数

2.3 网格划分及无关性验证

采用结构化网格对模型进行划分,同时进行网格自适应和无关性验证。如图2所示,以出口处0.03、0.05 mm晶体体积分数及结晶器内液相平均速度作为评价指标对网格进行验证。当网格数达到1 180 435后,3项指标结果随网格数量的继续增长变化很小。因此本文将计算域网格数设为1 180 435,网格最大畸变度为0.80,质量较好,满足计算需求。

图2 网格无关性验证结果Fig.2 Verification results of grid independence

2.4 模型验证

为验证模型准确性,对照文献[31],采用与模拟结构相似的结晶器进行连续冷却结晶的实验,利用数值模拟对文献中的实验数据开展模拟验证。实验研究了KCl溶液在结晶器中的结晶过程,入口温度为26 ℃,实验时间为晶体达到悬浮状态所用时间的8倍,利用粒度分析仪研究晶体粒度分布,得到相应实验数据。基于此实验,采用上述数学模型关联KCl结晶动力学模型,对KCl结晶过程进行模拟,将数值计算得到的结晶器内晶体平均粒度分布结果与实验数据进行对比,结果见图3。分析可知,验证值与实验值偏差较小,平均偏差3.65%,偏差可能是几何模型和边界条件的简化所致,因此可认为本文所用的数值模型准确可靠。

图3 晶体平均粒度分布实验值与验证值对比Fig.3 A comparison between experiment and verification results of average crystal size distribution

3 结果与分析

3.1 流动情况分析

3.1.1 结晶器内流动稳定性分析 图4为不同流动时间下结晶器轴向流场连续相体积分布图。可以看出,连续相在结晶器中心区域的分布要大于在边缘区域的分布,位于搅拌桨正下方的流域速度最小,区域内的介质交换与碰撞频率低,晶体生成少,连续相体积分数最大,为0.984 2。随着流动时间的增加,截面平均湍动能由0.042 m2/s2增大至0.042 5 m2/s2,混合程度变大。30 s后流场基本保持不变,结晶保持稳定。基于此,下文所进行的研究均采用流动时间为30 s时的结果。

(a)t=10 s (b)t=20 s

3.1.2 结晶器内流场特性分析 图5为结晶器轴向截面流场速度。物料在搅拌桨的作用下分散流动,搅拌桨附近流速最大,为1.91～2.11 m/s。导流筒内部的流体在搅拌桨的作用下速度较快,平均流速为0.878 m/s。外部的流体与内部存在明显的速度差。由图5右侧矢量图可以发现,流体流动过程呈现完整的内循环流动,流体由入口流入,由于桨叶形式为斜向上45°,所以流体在搅拌作用下向斜上方流动,由导流筒上方流出,沿着导流筒外部自上而下流到结晶器底部,从结晶器弧形底面回流至搅拌区域,形成内循环。

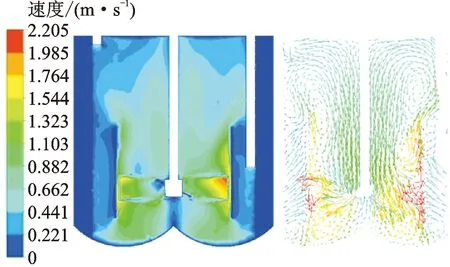
图5 轴向流场速度分布Fig.5 Axial flow field velocity profile

3.1.3 结晶器内温度分布 结晶器内温度分布如图6所示。从数值看,结晶器内温度几乎完全一致,最低温为253.146 K,最高温为253.15 K,可见在结晶器容量小、混合状态较好时,结晶所放出的结晶热非常小,结晶器内温度变化很小。也就是说,在对结晶过程进行数值模拟时,结晶对于温度场的影响可以忽略不计,此结论也在诸多前人研究中得以证实[32-34]。定性分析,母液由入口进入结晶器后温度迅速降低,逐渐与结晶器内温度平衡,结晶器下部温度略高于上部温度,因为结晶过程主要发生在下半区,所以区域内放出的结晶热使得下半区温度略高。

图6 结晶器内温度分布Fig.6 Temperature profile within crystallizer

3.2 晶体相分布分析

3.2.1 不同粒径晶体相分布 图7为不同粒径晶体的体积分数分布图。可以看出,不同粒径晶体分布趋势相近,晶体主要分布区域与流体主要流动区域保持一致,说明晶体在结晶器内的结晶与循环随流体流动进行。各粒径晶体主要位于结晶器挡板下半部分,此区域不仅位于流体主要流动区域内,各相间的传质与碰撞效应较大,而且由于挡板与底部自身的壁面效应,为晶体的附着与生长提供了大量的位点,有利于晶体成核与生长,其中晶体体积分数最大位置位于结晶器底部与壁面的顶角处,这是晶体重力沉积与流动双重作用的结果。随着粒径的增大,结晶器下部的分散相体积分数随之升高,说明大粒径晶体的悬浮程度变差,在结晶器底部积聚。

(a)0.01 mm (b)0.03 mm (c)0.05 mm

3.2.2 晶体相分布与流场关系 图8为0.05 mm晶体体积分数分布图,图9为轴向流场流线图。结合两图分析,晶体分布情况与流场具有极紧密的关系。在搅拌桨正下方存在一流动死区,物料无法流入此区域,导致此流动死区内基本无晶体分布。分析流线图,流体流动为总体内循环流动与局部涡流并存,主要涡流区域共6处,除搅拌桨桨端处的涡流外,其他涡流区域晶体体积分数均大于涡流区域附近的体积分数。由于涡流区域的粒子会围绕涡流中心旋转,并且涡流的特性为回旋的物质间距离很小,物质点的轨道紧凑,所以处于涡流区域内的晶体不易扩散,在涡流内的碰撞几率增大。至于搅拌桨桨端处,则是由于此位置流速过大,湍流程度强,湍动能为0.498 m2/s2,晶体在域内无法有效悬浮和停留,过大的流速也会导致晶体碰撞的动能增大,使新生晶核破碎,无法长大,所以此区域晶体分布很少。同理可以发现,流线图中流速大于1.40 m/s的位置,晶体的体积分数都很小,说明流速大于1.40 m/s时不利于溶液的结晶以及晶体的长大,在其余区域,随着流速的减小,晶体体积分数逐渐增加,因此在工业生产时,要控制结晶器内的流速不要超过1.40 m/s。

图8 0.05 mm晶体体积分数分布Fig.8 Volume profile of 0.05 mm crystals

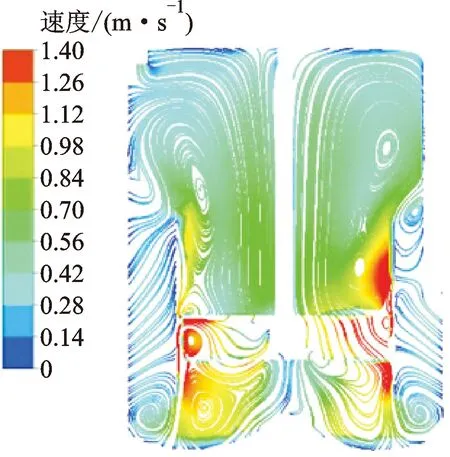
图9 轴向流场流线图Fig.9 A diagram of axial flow field streamline

3.3 晶体颗粒特性分析

为研究结晶器内晶体的颗粒特性,分别定量读取各晶体的粒度分布及不均匀度数据。其中不均匀度计算公式为

(16)

图10为不同粒径晶体在结晶器内的晶体不均匀度及粒度分布。粒径最小的0.01 mm晶体分布情况最好,不均匀度为0.000 7。因为其体积最小,在结晶器内的运动速度很快,所以流体赋予其的动能使得晶体更容易分散到结晶器各个部位。大粒径晶体由于其质量较大,搅拌桨所产生的升力对其作用有限,致使大粒径晶体无法充分流动,从而不均匀度逐渐增大,0.09 mm的晶体不均匀度达到0.051。对二甲苯晶体的粒度分布整体呈正态分布,其中0.01 mm晶体的数量最少,这是由于小颗粒在流体域内几乎完全悬浮,晶体与液相充分接触,因此小粒径晶体很容易随着结晶过程的进行生长为正常粒径的晶体。0.03～0.05 mm粒度范围内的晶体最多,占全部晶体的44.5%。随着晶体直径的增大,大粒径晶体的数量开始减少,由于大颗粒无法充分流动和悬浮,因此晶体的碰撞几率以及和溶液间的质量交换程度较低,晶体不易继续长大。

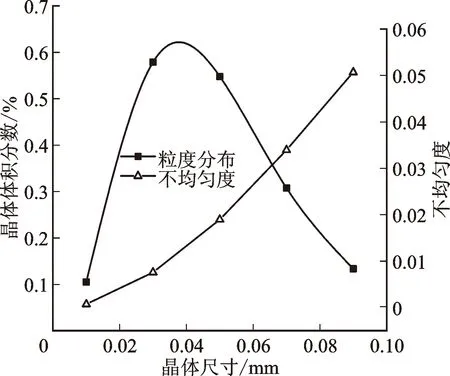
图10 晶体不均匀度与粒度分布Fig.10 Non-uniformity and particle size profile of crystals

4 结 论

为研究对二甲苯结晶过程与晶体积聚模式,耦合欧拉-欧拉模型与粒数衡算方程,利用分组法对粒数衡算方程进行求解,创新性地将粒数衡算方程转化为相间质量传递方程,并将其与对二甲苯结晶动力学进行关联模拟对二甲苯结晶,结论如下。

(1)结晶器内各组分混合程度与流动时间正相关,30 s后流场基本保持一致。导流筒内外部流速存在明显速度差,内部流速更快,最大速度区间为1.91～2.11 m/s。流体流动过程为内循环流动与局部涡流并存,各区域温度差异很小。

(2)晶体主要分布在结晶器下挡板及底部。搅拌桨正下方存在流动死区,死区内基本无对二甲苯晶体分布。当流速增大,对二甲苯体积分数逐渐减小,流速大于1.40 m/s时,晶体体积分数显著下降。涡流区域内的晶体体积分数大于涡流区域附近的体积分数。

(3)0.01 mm对二甲苯晶体在结晶器内分布情况最好,不均匀度为0.000 7,随着晶体粒径的增大,其不均匀度逐渐增加。

(4)对二甲苯晶体粒度呈正态分布,0.01 mm粒径晶体几乎完全悬浮,0.03～0.05 mm晶体数量最多,占晶体总量的44.5%,随着颗粒直径的增大,大粒径晶体的数量逐渐减少。