立式径向流吸附器传热传质过程模拟研究

徐攀,文键,彭荣梅,洪坤,李超龙,王斯民,厉彦忠

(1.西安交通大学能源与动力工程学院,710049,西安;2.浙江智海化工设备工程有限公司,313000,浙江湖州;3.西安交通大学化学工程与技术学院,710049,西安)

吸附器约占空分系统总能耗的16%,其作用是降低空气中杂质的浓度,使H2O的体积分数小于3×10-6,CO2小于10-6,碳氢化合物小于10-9[1]。立式径向流吸附器具有床层流动截面积大、空间利用率高、压降小等特点,被广泛用于大型空分设备中。张成芳等对吸附层内的流动进行理论分析,得到了流动均匀分布的流道静压分布条件,为吸附层流场均匀分布提供了理论依据[2]。文献[3-5]忽略了吸附过程对流场的影响,采用数值模拟方法研究了立式径向流吸附器的流场分布规律。文献[1,6]提出了分层并联和多组床层设计方法用于解决大型立式径向流吸附器能耗和流动均匀性的问题。在吸附层传热传质研究方面,Gang和Kapoor等通过一系列实验测定了分子筛吸附剂对CO2和H2O等气体的吸附特性,为研究吸附层的传热传质过程提供了实验依据[7-10]。王浩宇等采用数值模拟的方法对变压吸附制氧吸附器的吸附过程进行了研究[11-12]。文献[13-14]通过建立传热传质数值模型对Z型向心流动立式径向流吸附器内吸附过程进行了研究。目前大部分关于立式径向流吸附器的研究未考虑吸附层内传热传质过程,仅通过流动均匀性来衡量吸附性能[1-6],而不同结构立式径向流吸附器吸附层内的传热传质特性还不明确。因此,本文对立式径向流吸附器吸附层内CO2和H2O的吸附过程进行模拟研究,分析了流动均匀性和吸附性能的关系,揭示和对比了不同结构吸附器吸附层内的传热传质特性和吸附性能,为立式径向流吸附器的选择和设计提供了理论参考。

1 模型构建与验证

1.1 物理模型

如图1所示,立式径向流吸附器按照流动形式可以分为向心Z型、离心Z型、向心π型和离心π型等4种结构。本研究中向心流动和离心流动的同种吸附层的体积相等,但不同种类吸附层的位置不同,氧化铝层为活性氧化铝,分子筛层为分子筛13X。结合图1的模型结构和流动形式,不同结构的立式径向吸附器结构参数如表1所示。

1.2 数学模型

吸附层内传热传质过程的数学模型基于以下假设:①工作介质是由空气、CO2和H2O组成的单相、不可压缩理想气体;

②只考虑CO2和H2O的吸附过程,并且吸附热为定值,不随温度变化;③同种吸附层的填料均匀,吸附剂颗粒直径和孔隙率相等。基于以上假设,吸附层内传热传质过程的传质速率方程和吸附等温方程分别采用线性驱动模型(LDF)和扩展D-A模型[13,15]来描述。

LDF模型

(1)

扩展D-A模型[15,19]

(2)

组分质量守恒方程

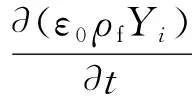
(3)

(4)

总的质量守恒方程

(5)

(6)

式中:ε0为孔隙率;ρf为气体密度,kg/m3;Yi为组分质量分数;u为速度,m/s;Dm,i为组分i的气体扩散系数,m2/s;Si为组分质量源项,kg/(m3·s);ρs为吸附剂密度,kg/m3;Mi为组分摩尔质量,kg/mol;Sm为总的质量源项,kg/(m3·s)。

动量方程

(7)

k方程

Gk+Gb-ρfε-YM+Sk

(8)

ε方程

(9)

式中:τ为应力张量,Pa;S为动量源项,kg/(m2·s2);k为湍动能,J;μ和μt分别为绝对黏度和湍流黏度,Pa·s;σk和σε分别为k和ε的湍流普朗特数;Gk为平均速度梯度引起的湍流动能;Gb为浮力产生的湍流动能;ε为湍动能耗散率;YM为可压缩湍流中膨胀对总耗散率的贡献;Sk和Sε分别为k和ε的源项;C1ε、C2ε和C3ε为常数。采用多孔介质模型简化处理吸附层内流动。对于填料均匀的吸附层,动量源项S表达式为

(10)

式中:α为渗透率,m2;C1为惯性阻力系数,m-1。α和C1的经验公式[16]为

(11)

(12)

式中:dp为吸附剂颗粒直径,m。对于格栅板,动量源项表达式为

(13)

C2的经验公式为

(14)

式中:φ为开孔率;δ为格栅板厚度,m;C为经验常数,与雷诺数Re和板厚孔径比δ/D有关(δ/D>1.6且Re>4 000时,C取0.98,其他情况取0.62)。

能量方程为

(15)

(16)

式中:Ef为气体含有的能量,J/kg;Es为固体含有的能量,J/kg;λe为床层有效导热系数,W/(m·K);T为温度,K;ΔHi为气体吸附热,J/mol。

吸附层和格栅板的结构和性能参数如表2所示。吸附器运行流量为2 000 m3/h,运行压力为101 325 Pa,入口气体温度为293 K,成分为空气、H2O和CO2,三者的体积分数比为99.76%∶0.20%∶0.04%。采用二维对称方式进行模型构建,采用Fluent基于压力的求解器,湍流模型选择标准k-ε模型,采用标准壁面函数处理近壁面处的流动,结合图1中不同形式的吸附器类型选择速度入口边界和压力出口边界。质量和能量源项通过UDF加载到Fluent中。压力离散格式为PRESTO!,各方程离散格式都采用二阶迎风格式,收敛残差均设为1×10-6。

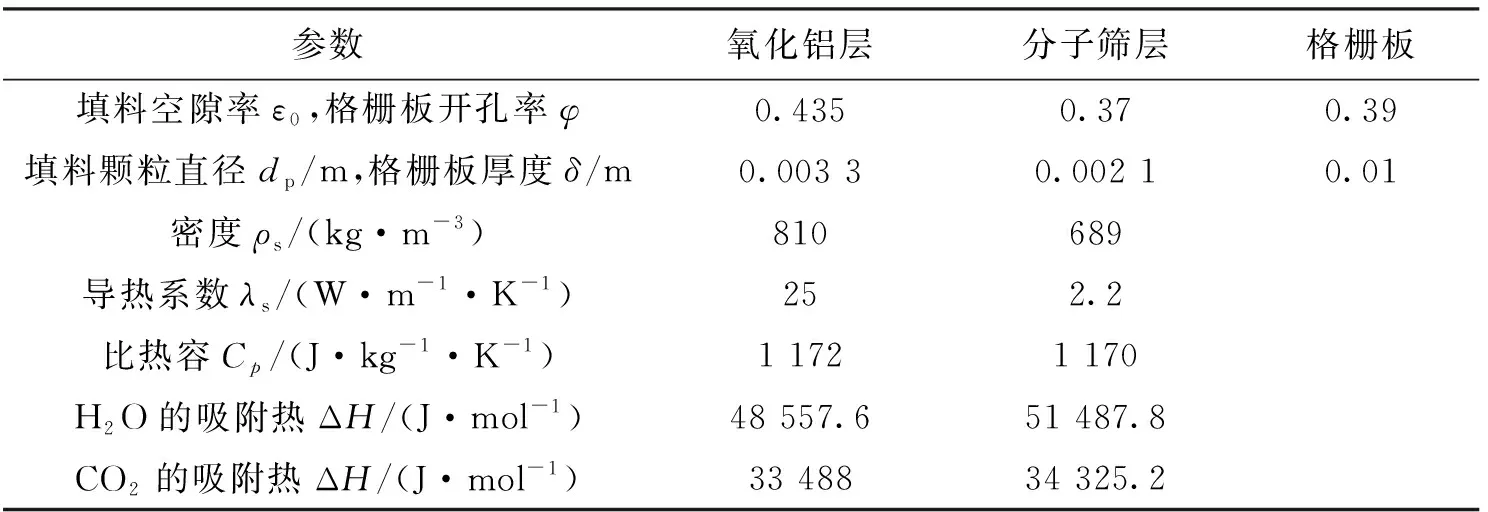
表2 吸附层和格栅板的结构和性能参数

1.3 模型验证

采用ANSYS meshing进行网格划分。为保证网格质量满足计算要求,以边界层网格形式对壁面和格栅板处的网格进行加密。以向心流动结构为例,区域离散化结果如图2所示。根据图3和表3可知,当网格数量≥8万、时间步长≤0.02 s后,吸附器的压降变化均小于0.1%,CO2和H2O穿透时间的变化均小于2%。因此,本研究选择网格尺寸为3 mm,网格数量为95 594,时间步长为0.02 s。

图2 向心流动结构的区域离散化结果Fig.2 Regional discretization results of centripetal flow structure

图3 网格无关性验证Fig.3 Verification of grid independence

采用文献[17]中的实验数据对数学模型进行验证,流动不均匀度的计算公式[17]为

(17)

式中:pA0-pB0代表入口侧吸附层压差,Pa;pAn-pBn代表出口侧吸附层的压差,Pa。根据表4可知,计算结果与文献[17]的实验结果的相对误差在允许误差范围内。

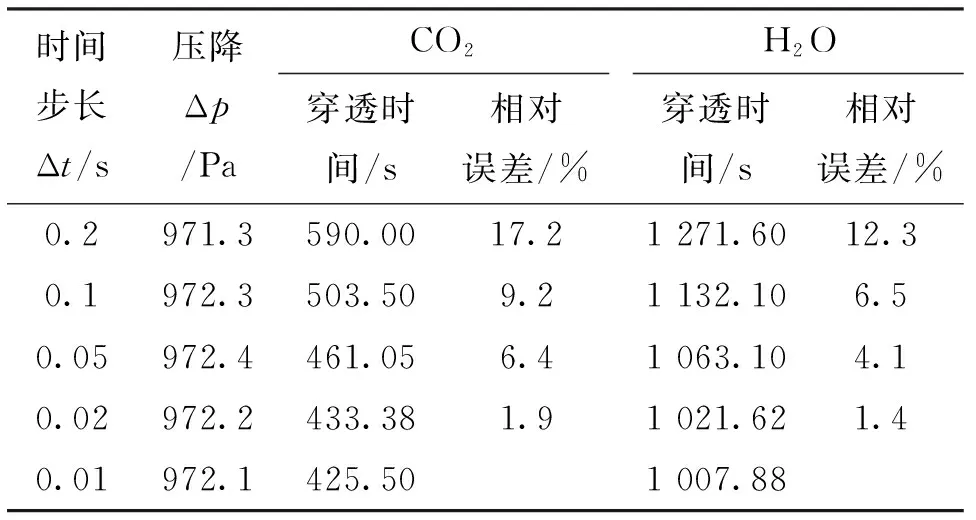
表3 时间步长无关性验证

表4 流动不均匀度对比

采用文献[9]的结构对吸附过程的传热传质数学模型进行验证,模拟的CO2穿透曲线与文献[9]实验数据对比如图4所示。其中,文献[9]中无量纲时间的计算公式为

(18)

式中:L为轴向变压吸附器的长度,m。考虑到实验测量误差和模拟计算简化假设,模拟的CO2的穿透时间与实验数据基本一致,由此验证了数学模型的准确性。

图4 CO2的穿透曲线对比Fig.4 A comparison of CO2 breakthrough curves

1.4 吸附器性能指标

能耗和吸附性能是吸附器最重要的两个性能指标。能耗指标用吸附器的进出口压差表示。结合H2O的体积分数小于3×10-6,CO2的体积分数小于10-6的标准,实际中CO2比H2O先穿透,因此本研究采用CO2的穿透时间作为吸附器吸附性能指标。文献中多采用流动均匀度来反映吸附器的吸附剂利用率和吸附性能,本文选择Fluent提供的流动均匀度计算公式

(19)

(20)

式中:ur为径向流动速度,m/s。记3层格栅板从外到内分别为1、2和3,并取其平均值作为吸附器的流动均匀度。

2 4种立式径向流吸附器的性能对比

2.1 流场分布

结合图5可知,吸附过程中流动均匀度无明显变化,说明吸附过程中吸附器内的流场分布基本保持不变,流动均匀性指标可视为吸附过程中反映吸附器流场分布的常量。

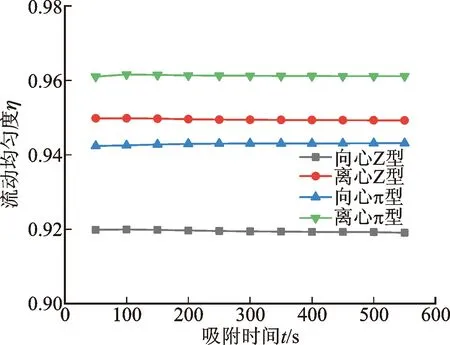
图5 4种吸附器流动均匀性随吸附时间的变化Fig.5 Variation of flow uniformity of four kinds of adsorbers with adsorption time

4种结构的流场分布如图6所示,向心流动的两种吸附器气体经导流区进入环形流道,再依次经氧化铝层和分子筛层进入中心流道,最后向上或向下流出吸附器;离心流动的两种吸附器气体先进入中心流道,再依次经氧化铝层和分子筛层进入环形流道,最后经导流区流出吸附器。4种吸附器内,沿着气体流动方向,静压不断降低,主要的压降区域在氧化铝层和分子筛层。

(a)静压分布

压降方面,向心Z型(974.3 Pa)>离心π型(857.2 Pa)>向心π型(856.8 Pa)>离心Z型(828.3 Pa);以向心Z型为基准,离心π型的压降相对于向心Z型降低了12.0%,向心π型的压降相对于向心Z型降低了12.1%,离心Z型的压降相对于向心Z型降低了15.0%。流动均匀性方面,两种流动均匀度均为:离心π型(0.961 1)>离心Z型(0.949 3)>向心π型(0.943 1)>向心Z型(0.919 3)。

2.2 吸附传热传质过程

(1)向心Z型。向心Z型的CO2穿透时间为433.38 s,吸附时间100、300、433.38和600 s时CO2和H2O的体积分数分布如图7所示。对于向心Z型,CO2的穿透区域是上侧的吸附层区域,H2O的穿透区域是下侧的吸附层。

(a)CO2体积分数分布

如图8所示,温度较高的区域是下侧的吸附层区域,该区域主要是H2O的吸附。格栅板径向流速和吸附层压降分布如图9所示,进吸附层格栅板的径向流速主要受氧化铝层压降影响,出吸附层格栅板的径向流速主要受分子筛层压降的影响,吸附层内格栅板径向流速受两层吸附层压降的作用,吸附层上侧的压降较大从而使进出吸附层的气体的速度分布(格栅板1和格栅板3)均为上侧速度明显均大于其他位置,因此上侧的吸附层区域为最先穿透位置。

图8 向心Z型吸附过程温度分布Fig.8 Temperature distribution in adsorption process of centripetal Z-type

图9 向心Z型径向流速和吸附层压降分布Fig.9 Distribution of radial velocity and pressure drop of adsorption layers with centripetal Z-type

(2)离心Z型。离心Z型的CO2穿透时间为550.84 s,吸附时间100、300、550.84和600 s时CO2和H2O的体积分数分布如图10所示。对于离心Z型,CO2和H2O的穿透区域均是下侧的吸附层区域。

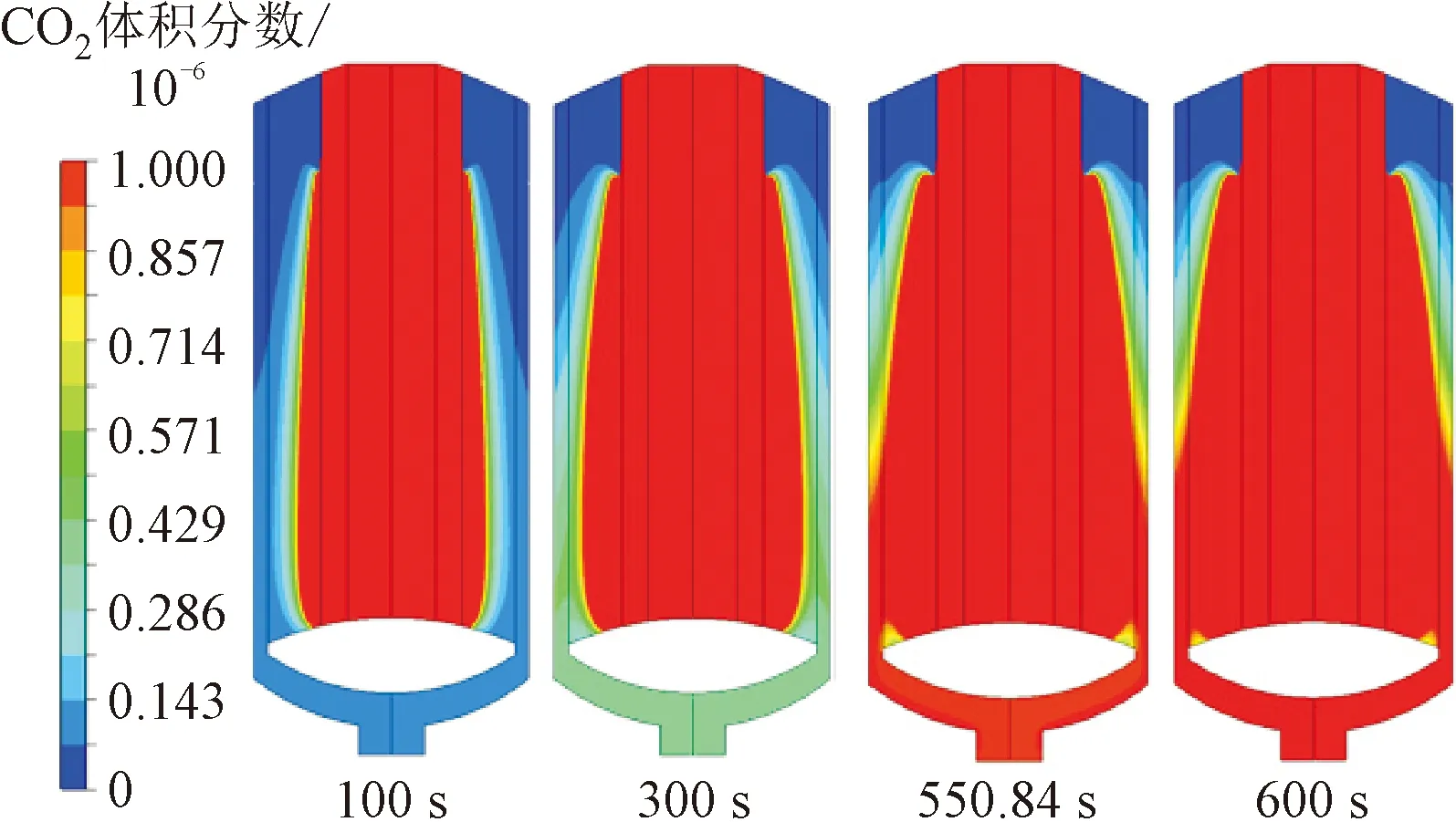
(a)CO2体积分数分布

如图11所示,温度较高的区域由上侧转移到中部偏下侧的吸附层区域,该区域是CO2和H2O的主要吸附区域。格栅板径向流速和吸附层压降分布如图12所示,受吸附层压降分布的影响,进吸附层(格栅板3)的下侧速度均大于其他位置,出附层(格栅板1)的中部偏下侧速度较大,因此中部偏下侧的吸附层区域为最先穿透位置。

图12 离心Z型径向流速和吸附层压降分布Fig.12 Distribution of radial velocity and pressure drop of adsorption layers with centrifugal Z-type

(3)向心π型。向心π型的CO2穿透时间为552.38 s,吸附时间100、300、552.38和600 s时CO2和H2O的体积分数分布如图13所示。对于向心π型,CO2和H2O的穿透区域均是下侧的吸附层区域。

(a)CO2体积分数分布

如图14所示,温度较高的区域在下侧的吸附层,该区域是CO2和H2O的主要吸附区域。格栅板径向流速和吸附层压降分布如图15所示,受吸附层压降分布的影响,进吸附层(格栅板1)的速度是下侧速度凸起并大于其他位置,出吸附层(格栅板3)的速度是下侧速度明显大于其他位置,因此下侧的吸附层区域为最先穿透位置。

图14 向心π型结构吸附过程中温度分布Fig.14 Temperature distribution in adsorption process of centripetal π-type

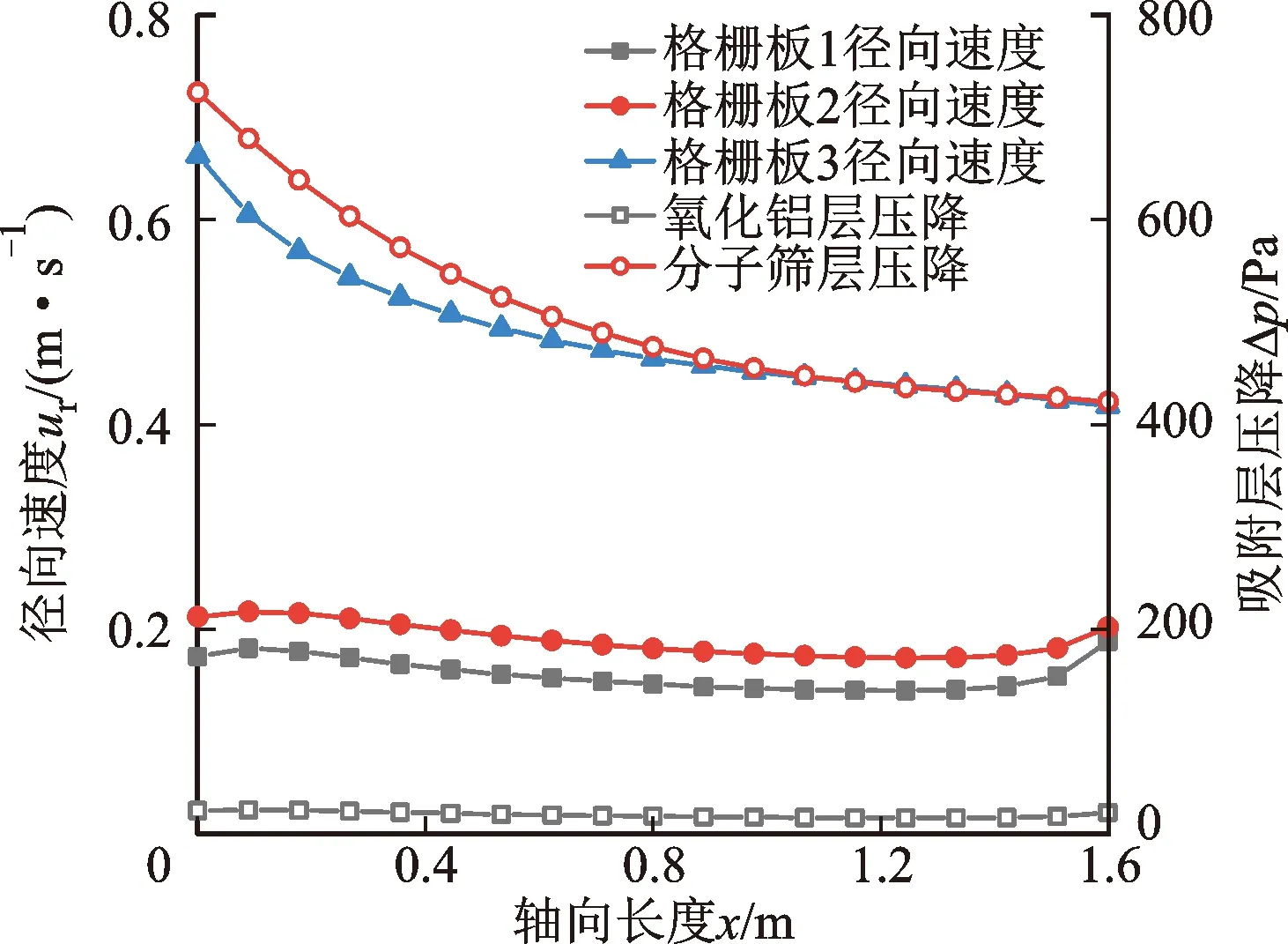
图15 向心π型径向流速和吸附层压降分布Fig.15 Distribution of radial velocity and pressure drop of adsorption layers with centripetal π-type

(4)离心π型。离心π型的CO2穿透时间为969.8 s,吸附时间200、400、600和969.8 s时CO2和H2O的体积分数分布如图16所示。对于离心π型,CO2和H2O的穿透区域均是上侧的吸附层区域。

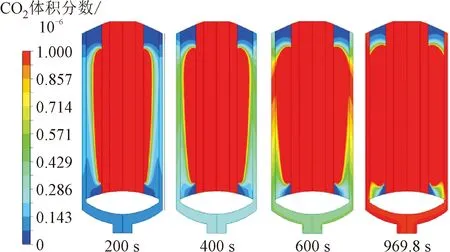
(a)CO2体积分数分布

如图17所示,温度较高的区域由下侧的吸附层区域转移到上侧的吸附层区域,该区域是CO2和H2O的主要吸附区域。格栅板径向流速和吸附层压降分布如图18所示,受吸附层压降分布的影响,进吸附层(格栅板3)的下侧速度略大于其他位置,出附层(格栅板1)的速度是上侧速度有凸起并大于其他位置,因此上侧的吸附层区域为最先穿透位置。

图17 离心π型吸附过程温度分布Fig.17 Temperature distribution in adsorption process of centrifugal π-type

图18 离心π型径向流速和吸附层压降分布Fig.18 Distribution of radial velocity and pressure drop of adsorption layers with centrifugal π-type

对比4种形式吸附器的吸附过程,不同结构的吸附器的穿透区域和主要吸附区域不同。向心Z型结构的CO2与H2O穿透区域不同,其他3种结构的CO2与H2O穿透区域相同。向心Z型、离心Z型和离心π型的CO2穿透区域和主要吸附区域均为与进气侧相对的吸附层区域,向心π型的CO2穿透区域和主要吸附区域为进气侧吸附层区域。

2.3 性能对比

4种结构立式径向流吸附器的性能对比如表5所示,向心π型的CO2和H2O穿透时间相隔最近,其他3种结构基本上H2O穿透时间都是CO2穿透时间的2倍多。虽然入口气体中H2O的体积分数是CO2的5倍,但是氧化铝和分子筛层对H2O的吸附能力远大于CO2并且会优先吸收H2O,因此CO2穿透时间快于H2O。4种结构的吸附性能为:离心π型>向心π型>离心Z型>向心Z型,以向心Z型的吸附时间为基准,离心π型的吸附时间是向心Z型的2.34倍,向心π型的吸附时间是向心Z型的1.28倍,离心π型的吸附时间是向心Z型的1.27倍。流动均匀性指标在吸附过程中为反映吸附器流场分布的参数,根据表5可知,流动均匀性指标与吸附器吸附性能变化规律相近,因此采用流动均匀性反映吸附器的吸附剂利用率和吸附性能是合理的。综合对比4种结构的吸附器的性能,离心π型的性能最好,吸附时间为969.8 s, 是向心Z型的2.34倍,压降为857.2 Pa,相对于向心Z型降低了12.0%。

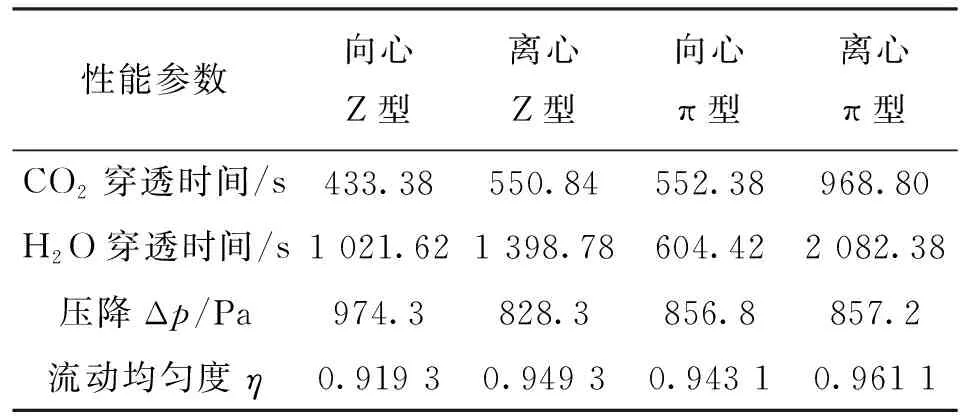
表5 4种结构的吸附性能对比

3 结 论

(1)流动均匀性指标是吸附过程中反映吸附器流场分布的常量,与吸附性能变化规律相近,可用于侧面反映立式径向流吸附器的吸附剂利用率和吸附性能。

(2)向心Z型结构的CO2与H2O穿透区域不同,其他3种结构的CO2与H2O穿透区域相同。

(3)向心Z型、离心Z型和离心π型的CO2穿透区域和主要吸附区域均为与进气侧相对的吸附层区域,向心π型的穿透区域和主要吸附区域为进气侧吸附层区域。

(4)综合对比4种形式吸附器的性能,离心π型的性能最好,压降为857.2 Pa,相对于向心Z型降低了12.0%,吸附时间为969.8 s,是向心Z型的2.34倍。