叶端定时中多重信号分类法的滤波特性研究

压气机是航空发动机上的关键功能性部件,其叶片直接与外界空气接触,易遭受外物打伤,从而产生损伤,进一步导致转子故障,严重危害航空发动机运行安全

。状态监测是故障诊断和健康管理的基础,需要获取能够反映设备运行状态的关键参数。固有频率作为能够反映叶片形态变化的关键参数,一直以来是研究的重点

。

叶端定时是一种非接触式测量手段,具有非侵入式的特性,有望实现旋转叶片在线监测

。叶端定时信号的欠采样特点使得抗混叠频谱分析方法成为了叶端定时信号处理领域的研究热点

。稀疏表示根据叶端定时信号的频域稀疏特性,对频谱系数进行正则约束,同时选择合适的损失函数,将频谱分析转化为优化问题

。Pan等使用基追踪降噪算法分析叶片的多模态振动,降低了测量不确定性对频域重构结果的影响

。吴淑明等将增强稀疏分解应用于频谱分析,通过对正则项进行加权并迭代更新权重,缓解

范数对各系数惩罚程度不均的情况

。Bouchain等基于正交匹配追踪(OMP),提出了计算效率更高、更准确的Block-OMP以获得频谱

。除此之外,基于最小二乘拟合

、非均匀傅里叶变换

、中国余数定理

的方法也得到广泛应用。非均匀传感器布局是克服叶端定时信号频谱混叠现象的必要条件,前述频谱分析方法均采用了非均匀传感器布局。通常信号非均匀性的来源如下:数据丢失,随机采样装置以特定分布采样,采样装置的均匀采样网格随机抖动,采样装置遵循周期采样模式但同一周期内是非均匀性的。恒定转速下,叶端定时信号的非均匀性属于最后者,这种非均匀采样模式也被称为半均匀采样。Wang等基于半均匀采样模式,提出了适用于叶端定时信号分析的改进多重信号分类法(MUSIC),实现了欠采样信号频谱分析

。笔者前期对MUSIC方法进行的大量仿真及实验表明:MUSIC方法无法识别同步频率分量。这一“坏现象”可以理解为,MUSIC方法具有滤除同步频率分量的特性。同步频率分量定义为转频的倍频分量,故该滤波特性能突出叶片非共振区频谱中的异步频率分量——固有频率。

本文对MUSIC方法中的信号子空间生成过程进行分析,将其类比于主成分分析中的主成分生成过程。进一步分析得到,同步频率分量与异步频率分量对应的信号子空间的区别,通过导向矢量和信号子空间的空间关系对该滤波现象进行数学解释。同时,通过仿真和实验,证明了存在该滤波特性以及所给数学解释的合理性。

1 叶端定时测量原理

叶端定时传感器通常具有激光

、电容

、电涡流

、微波

等传感器类型。本文以激光传感器为例,对叶端定时技术进行简要介绍。如图1所示,传感器按用途分两类:第1类传感器安装于机匣上,用于采集叶片到达时间,称为叶端传感器;第2类传感器安装于转轴附近,用于采集转速参考信号,称为转速参考传感器。当叶片或转轴标记经过激光传感器时,传感器接收到的反射光强度会随着反射面的变化而改变,继而在后端电路产生叶片信号或转速参考信号。

理想叶片到达时间可以通过理想叶片到达角度计算得出,其表达式为

=

2π

(1)

式中:

为实测转速参考信号相邻两个转速脉冲时间之差;

为理想叶片到达角度。

可由传感器和转轴标记的相对位置计算得出,或在恒定低转速条件下,测得连续多个实际叶片到达时间,通过式(1)反算出实际叶片到达角度并平均得到。

基于式(1),叶片振动位移表达式为

西雅图通过收集并分析从市区建筑物管理系统中得来的众多数据集，通过预测分析，找出哪里可以减少能源使用，或者根本不需要使用能源。项目的目标是将该地区的电力消耗减少25%。

(3)对自相关矩阵进行特征值分解。将特征值从大到小排序为

≥

≥…≥

,前

个特征值对应的特征向量构成信号子空间

,其余

-

个特征值对应的特征向量构成噪声子空间

,且满足

=2π

(

-

)

(2)

式中:

为转子半径;

为实际叶片到达时间。

2 MUSIC方法

MUSIC方法的叶片振动位移信号如下

(3)

式中:

为频率分量的个数;

、

、

分别为第

个频率分量的幅值、频率、相位;

为白噪声。基于上述信号模型,对MUSIC方法的步骤进行阐述。

(1)构建快拍矩阵。第

个快拍矢量为

社会的发展促进审计目标的不断革新，而审计目标的革新也带动着审计技术的进步。而在众多的组织和集团之中，银行无疑是对内部审计标准要求最高的，业务和项目中一旦存在缺陷与风险，就会给银行带来难以想象的损失。因此在审计技术上，各大商业银行均需要保持着高度的重视，比如常见的以内部控制评价为基础的现代审计方法，还有新兴的“风险导向”审计方法等，都是走在时代前沿的科学灵活的现代审计技术。

(

)=

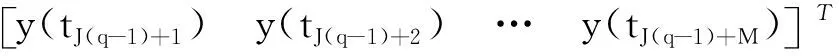
(4)

托伐普坦治疗肝硬化腹水伴低钠血症疗效与安全性的Meta分析 …………………………………………… 李春杏等（6）：833

(5)

(2)计算自相关矩阵。样本自相关矩阵为

由于真实信号的频率分量数无法得知,本文采用阈值法确定频率分量数,通过人为设定阈值

,频率分量数

满足

(6)

Classification of occurrence form of spheric weathered granite and stability analysis LIU Zhi-jun, WANG Xian-neng, MO Li(40)

2.炒锅置火上，放菜油烧至四成热，下干辣椒节炒几下，再下牛油炒热放豆瓣酱炒香，下姜片、蒜片，炸出香味，倒入鲜汤，用大火烧沸，下醪糟汁、精盐、冰糖，熬 10 min，下花椒熬出香味，舀入火锅中，打去浮沫，加入味精，即为汤汁。火锅点火，放入红枣、猪蹄块、蹄筋煮沸，便可随意烫食。

=0

(7)

(2)环境干预:护理人员每日上午10点、下午3点对打开病房窗户,通风换气,保持房间湿度在60%左右,温度在24℃左右,室内光线明暗适宜,力求给予患儿干净、整洁、安静、舒适的治疗环境。

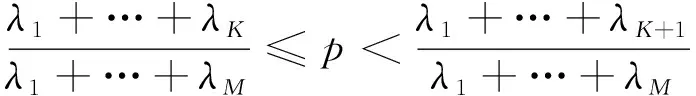
(8)

(4)设定频率遍历区间及步长,进行频率遍历。在遍历过程中,给定频率

的导向矢量表达式如下

(9)

(10)

3 MUSIC方法滤波特性

信号子空间的生成原理类似于主成分分析中主成分的生成

。MUSIC方法中特征值分解的实质是进行坐标变换,按照方差最大化思想为快拍矩阵中的快拍矢量确定新的投影坐标系,即信号子空间。

为便于后续分析,假设叶片振动信号中只存在单个频率分量

。首先讨论复指数信号情况,由上节可知,单个频率分量经特征值分解,得到信号子空间为单个复数列向量

,所有快拍矢量

(

)都可以通过复数系数

乘

得到。将该复数系数表示为

=

e

j

,其中

为控制幅值,

为控制相位。该复数系数所在平面可表示为极坐标系,则该坐标系平面能够表示所有频率为

的复信号对应的

维向量,且该平面上的点对应的向量都与噪声子空间正交。如图2所示,频率为

的单位导向矢量可以表示为该平面中单位圆上的一个点,与噪声子空间正交。

嫩柳新裁，小桃初绽，几分春色轻柔。恁莺声娇软，浸染枝头。问取绿前红后，三两啭、应是含羞。浑不觉，天涯倦客，误了归舟。 休休。一川逝水，载缕缕相思，竟自东流。念五亭桥远，塞外凝愁。可有行云顾我？声声雁、过尽江楼。东风里，谁曾识得，梦在西州。

实际的叶片振动位移为实信号,实信号情况下的导向矢量表达式如下

(

)=

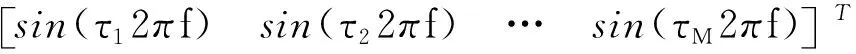
(11)

对连续化疗的患者，临床护士应重视其焦虑状态的累积作用和变化规律，在不同时期，采取针对性的护理措施如适时有效地开展健康宣教、心理支持疗法、减轻化疗副作用的护理方案等。要特别重视一个疗程中最后1次化疗前患者出现的焦虑状态，帮助患者和家属增强治疗的信心和充分做好迎接下次化疗的生理和心理准备。

在光华闪耀的粉蓝色或棕色珍珠母贝星空中，白色珍珠母贝月亮展现从新月到满月的各种形态。两轮月亮在6点钟位置的镂空拱形钻石格栅下方旋转，如同捉迷藏一般，玩趣十足。格栅由九道金质镶钻轮幅组成，开放区域显示当前月相。钻石格栅的整个表面细密镶嵌93颗圆形明亮式切工钻石，中央点缀一颗醒目钻石。鉴于空间极小，爪镶难以实现，精细微镶再次彰显海瑞温斯顿宝石镶嵌师的高超技艺。

仿真叶片振动信号表达式如下

(

)=

+

(12)

式中:

、

分别为

、

在线性组合中的系数。以

、

作为单位向量,建立直角坐标系,坐标系平面上的点表示所有频率为

的正余弦信号对应的

维向量,均与噪声子空间正交。如图3所示,频率为

的单位导向矢量为该平面中单位圆上的点,与噪声子空间正交。

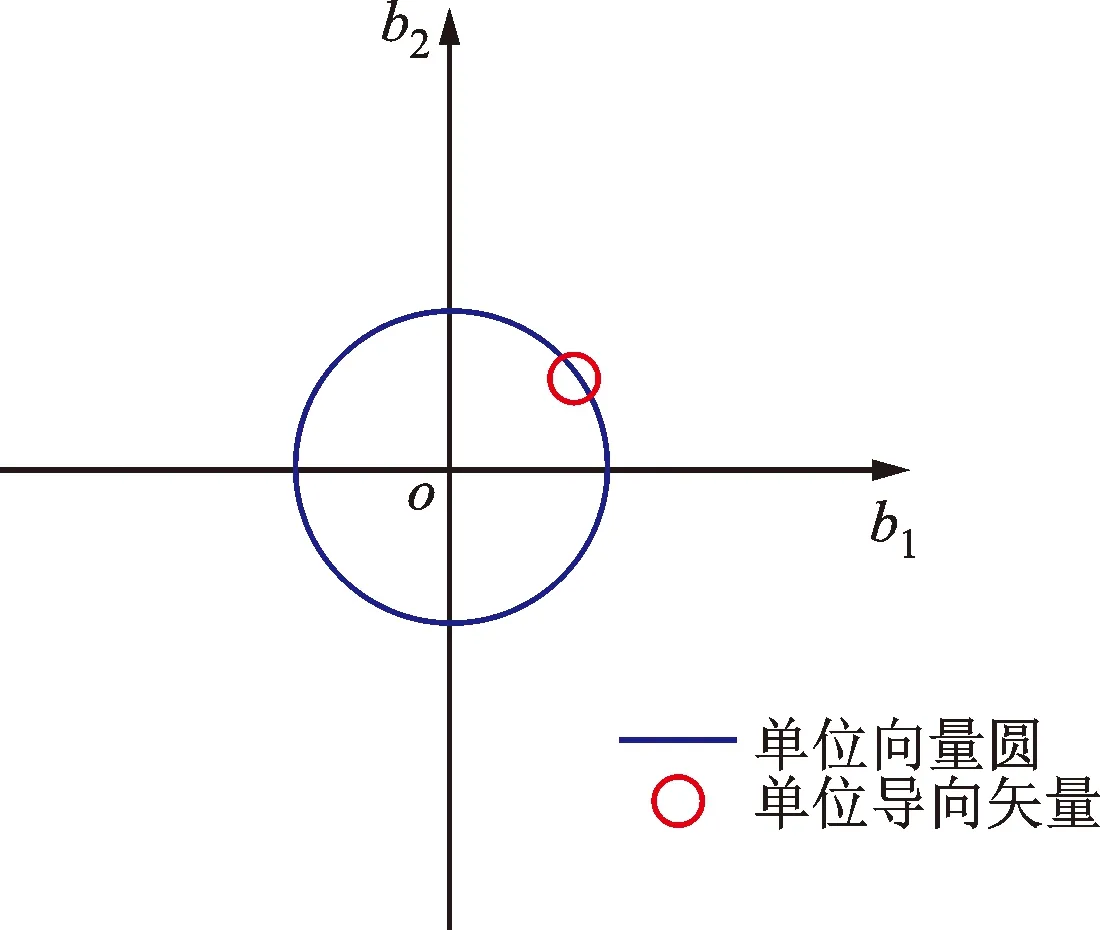
当

为同步频率分量时,所有快拍矢量完全相同。自相关矩阵经特征值分解得到的信号子空间只存在单个列向量

。快拍矢量可由

表示,

为权重。以

为单位向量、

为坐标值的坐标轴表示所有频率为

、相位与快拍矢量相同的

维向量。人为设置的频率为

的导向矢量与快拍矢量的相位不会恰好相同,导向矢量位于该坐标轴以外,如图4所示。由于自相关矩阵的特征向量相互正交,在特征向量构成的

维空间中,导向矢量不属于信号子空间,故其与噪声子空间不正交。

值得讨论的是,当频率分量

为同步频率分量时,相邻快拍矢量的相位相差为2π,所有快拍矢量完全相同。当频率分量

为转频的0

5、1

5、2

5……倍时,相邻快拍矢量的相位相差为π。就数值角度而言,该情况下快拍矩阵

中相邻的快拍矢量对应维度上的值互为相反数,即

(

)=-

(

+1),0<

<

。就空间角度而言,快拍矢量可看作

维空间中一条以零点为起点的向量,相位相差π代表相邻的快拍矢量方向相反,即所有的快拍矢量均处在一条直线上。特征值分解后的信号子空间也仅存在单个列向量

,故此种情况的分析结果与同步频率分量时相同。

4 仿真验证

区别于复指数信号,实信号的自相关矩阵经特征值分解后,单个频率分量

对应于信号子空间中两列相互正交的列向量

和

。具有不同相位的快拍矢量可以由

和

的线性组合得到

(

)=

sin(2

+

)+

sin(2

+

)+

(

)

(13)

通过设置不同参数对同步频率分量、异步频率分量以及混合频率分量进行仿真。信噪比

设置为4,转频

=124 Hz。MUSIC方法参数设置:快拍个数

=100,快拍矢量长度

=120,频率遍历范围[1 Hz,1 000 Hz],步长为1 Hz。基于最小冗余传感器布局,选择的传感器布置角度为(0°,15°,165°,225°),故仿真起始时间

=0

。

式中:

为叶端传感器的个数,

为快拍矢量的长度,满足mod(

,

)=0。

个快拍矢量构建成的快拍矩阵

的表达式如下

4.1 异步频率分量

首先验证MUSIC方法识别异步频率分量的有效性。设置

=1,

=405 Hz,

=0

3π,

=0。

非

的整数倍,该频率分量为异步成分。导向矢量设置为

(

)=

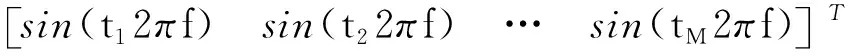
(14)

导向矢量与首个快拍矢量

(1)相位相差为0

3π。异步频率分量的各快拍矢量相位取决于传感器布局以及转频与异步频率分量的关系。

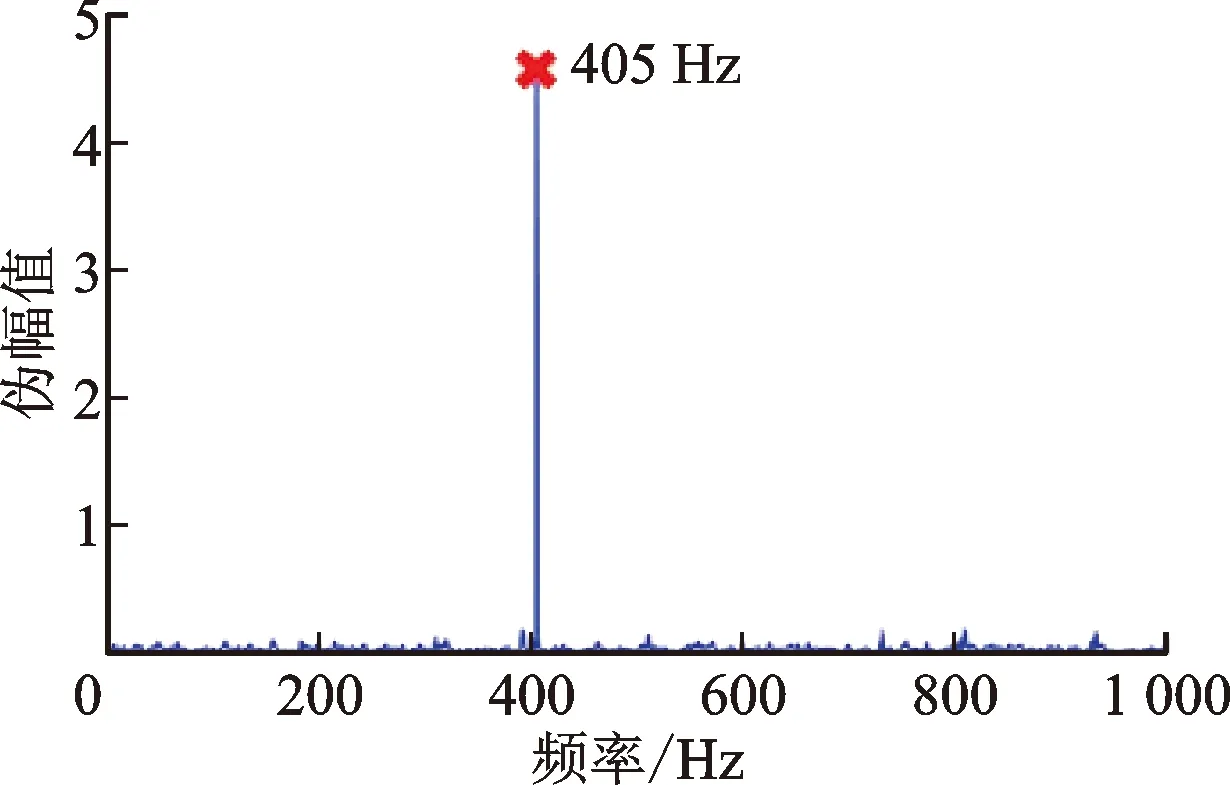
如图5所示,

=405 Hz能够被准确识别。证明了对于异步频率分量,导向矢量的相位可以任意设置而不影响MUSIC方法频率识别的有效性。

式(11)中的正弦函数也可用余弦函数替代,等价于将

(

)的相位移动0

5π。

4.2 同步频率分量

由第3节的推导可知,当导向矢量与快拍矢量相位相同时,同步频率分量才能够被识别,即图4中的导向矢量

(

)位于坐标轴上。设置

=1,

=620 Hz,

=0

4π,

=0。

为

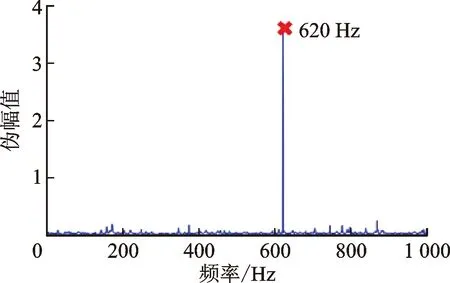
的5倍,为同步频率分量。导向矢量设置同式(14),导向矢量和快拍矢量相差0

4π。如图6a所示,由于

(

)不属于信号子空间坐标轴,故

无法被正确识别。

设置导向矢量相位与快拍矢量相位相同

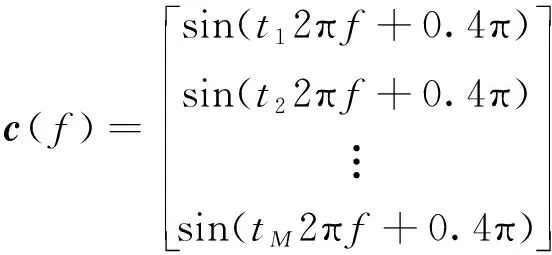
(15)

此时,导向矢量位于信号子空间坐标轴上。重新分析伪谱,如图6b所示,

=620 Hz能够被准确识别。证明了只有当导向矢量与快拍矢量相位相同时,同步频率分量才能够被正确识别。

4.3 混合频率分量

设置

=1,

=620 Hz,

=0

4π;

=1,

=405 Hz,

=0

3π。导向矢量设置同式(14),伪谱如图7所示,同步频率分量

=620 Hz被过滤,异步频率分量

=405 Hz被保留,证明了MUSIC方法对同步频率分量的滤波特性。

当还是孩子的时候，他曾试图用一只旧的禄莱可德（ROLLEICORD）相机拍摄上帝。有人告诉他一位拉比曾见过上帝。威特金拜访了这位拉比，但是没有见到上帝。到哪儿去找上帝呢，他问自己。是如基督教所训示的，在人群之中？那么又在什么人之中呢？难道没有可能，上帝恰恰是通过那些在身体或精神上迥异于主流人群的人来示现自身？实际上，乔-彼得·威特金的创作核心，反映的正是类似这样的哲学思考。

4.4 鲁棒性分析

为探究MUSIC方法对同步频率分量的过滤特性在不同噪声情况下的体现,基于4.3节的参数设置情况,设置信噪比为[-5 dB,5 dB],步长0.5 dB,伪谱最大值对应的频率作为

=405 Hz的估计值。在每个

下进行50次蒙特卡罗测试,将平均绝对误差作为误差指标。如图8所示,信噪比较低时,MUSIC方法分析误差较大,随着信噪比提高,误差减小,异步频率分量在伪谱中逐渐占据突出地位。

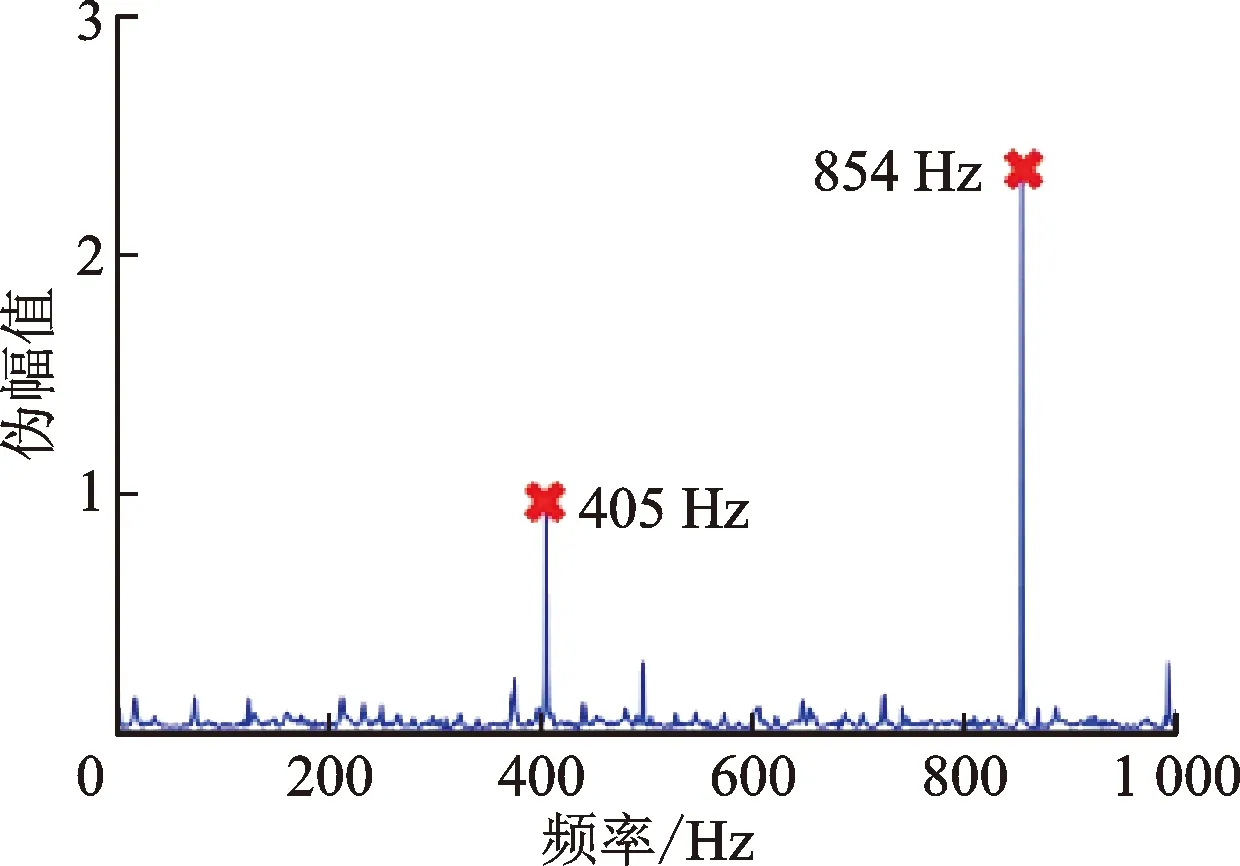
为探究多个同步频率分量和多个异步频率分量情况下MUSIC方法滤波特性的有效性。设置

=1,

=620 Hz,

=0

4π;

=1

5,

=405 Hz,

=0

3π;并增加两个频率分量

=1

5,

=372 Hz,

=0

1π;

=1,

=854 Hz,

=0

6π。伪谱如图9所示,同步频率分量

=5

、

=3

被过滤,异步频率分量

、

被保留。

以上数据显示全国房地产市场综合实力百强企业的市场份额即CR100从2011年的26.2%增加至2017年的47.7%，增长率为82.1%。从10强和百强企业的数据对比分析来看，二者均表明全国房地产市场集中度在不断增强，但10强企业的市场份额的提升速度稍快于百强企业，这说明随着中国房地产市场发展，大企业规模增长有所加快，市场集中度仍有较大提升空间。不过，按照贝恩的市场结构分类标准，当前全国房地产市场仍处于竞争型市场结构，市场集中度虽有所增长但仍处于偏低水平，这是对中国房地产业市场结构的一个基本判断。

5 实验验证

5.1 实验设置

叶端定时实验台如图10所示,叶盘直径为196 mm,材料为钛合金TC4。4个叶端传感器角度间隔为0°、15°、150°。因为传感器的周向布置存在周期性,该布局与仿真布局(0°,15°,165°,225°)等价。叶盘的气体激励施加方式见图11。转速传感器安装位置如图12所示,实验转频

≈148.4 Hz。

5.2 MUSIC方法滤波特性实证

MUSIC方法参数设置:快拍个数

=100,快拍矢量长度

=140,频率遍历范围[1 Hz,1 200 Hz],遍历步长为1 Hz。所分析的原始位移数据如图13所示,最小二乘拟合频谱被用作证明同步频率分量的存在,如图14所示,频率混叠现象导致最小二乘频谱具有明显的周期性。MUSIC方法伪谱如图15所示,可以看出,MUSIC方法不仅过滤了同步频率分量,并且克服了频率混叠现象。结合在转频为148 Hz时的叶盘一阶固有频率为817 Hz的先验知识,可验证MUSIC方法频率辨识的有效性。

6 结 论

(1)当转频的倍频与叶片的固有频率不重合时,叶片处在非共振区,此时叶片振动信号包含同步频率分量和异步频率分量两种类型的振动成分。

(2)MUSIC方法能够滤除叶片振动信号中的同步频率分量,通过分析MUSIC方法中信号子空间生成和主成分分析中主成分生成之间的一致性,从导向矢量与信号子空间的关系上给出了倍频滤波现象的数学解释。

(3)在叶端定时信号处理中,MUSIC方法能够克服由欠采样导致的频率混叠现象。

:

[1] 寇海军, 张俊红, 林杰威. 航空发动机风扇叶片振动特性分析 [J]. 西安交通大学学报, 2014, 48(11): 109-114.

KOU Haijun, ZHANG Junhong, LIN Jiewei. Aero-engine fan blade vibration characteristic analysis [J]. Journal of Xi’an Jiaotong University, 2014, 48(11): 109-114.

[2] ABDELRHMAN A M, HEE L M, LEONG M S, et al. Condition monitoring of blade in turbomachinery: a review [J]. Advances in Mechanical Engineering, 2014, 6: 210717.

[3] FORBES G L, RANDALL R B. Estimation of turbine blade natural frequencies from casing pressure and vibration measurements [J]. Mechanical Systems and Signal Processing, 2013, 36(2): 549-561.

[4] 王维民, 陈子文, 张旭龙, 等. 基于叶端定时的转子碰摩故障诊断方法 [J/OL]. 航空学报, 2021 [2021-02-19]. http: ∥kns.cnki.net/kcms/detail/11.1929. v.20210225.1634.032.html.

WANG Weimin, CHEN Ziwen, ZHANG Xulong, et al. Fault diagnosis method of rotor rubbing impact based on blade tip timing [J/OL]. Acta Aeronautica et Astronautica Sinica, 2021 [2021-02-19]. http: ∥kns. cnki.net/kcms/detail/11.1929.v.20210225.1634.03 2.html.

[5] KHARYTON V, DIMITRIADIS G, DEFISE C. A discussion on the advancement of blade tip timing data processing [C]∥ASME Turbo Expo 2017: Turbomachinery Technical Conference and Exposition. New York, NY, USA: ASME, 2017: V07BT35A002.

[6] CHEN Zhongsheng, SHENG Hao, XIA Yemei, et al. A comprehensive review on blade tip timing-based health monitoring: status and future [J]. Mechanical Systems and Signal Processing, 2021, 149: 107330.

[7] CHEN S S, DONOHO D L, SAUNDERS M A. Atomic decomposition by basis pursuit [J]. SIAM Review, 2001, 43(1): 129-159.

[8] PAN Minghao, YANG Yongmin, GUAN Fengjiao, et al. Sparse representation based frequency detection and uncertainty reduction in blade tip timing measurement for multi-mode blade vibration monitoring [J]. Sensors, 2017, 17(8): 1745.

[9] 吴淑明, 胡海峰, 赵志斌, 等. 增强稀疏分解及其在叶片振动参数识别中的应用 [J]. 机械工程学报, 2019, 55(19): 19-27.

WU Shuming, HU Haifeng, ZHAO Zhibin, et al. Enhancing sparse decomposition based blade vibration parameter identification [J]. Journal of Mechanical Engineering, 2019, 55(19): 19-27.

[10]BOUCHAIN A, PICHERAL J, LAHALLE E, et al. Blade vibration study by spectral analysis of tip-timing signals with OMP algorithm [J]. Mechanical Systems and Signal Processing, 2019, 130: 108-121.

[11]WU Shuming, RUSSHARD P, YAN Ruqiang, et al. An adaptive online blade health monitoring method: from raw data to parameters identification [J]. IEEE Transactions on Instrumentation and Measurement, 2020, 69(5): 2581-2592.

[12]LIU Zhibo, DUAN Fajie, NIU Guangyue, et al. An improved circumferential fourier fit (CFF) method for blade tip timing measurements [J]. Applied Sciences, 2020, 10(11): 3675.

[13]王文杰, 李小平. 鲁棒的闭式中国余数定理及其在欠采样频率估计中的应用 [J]. 信号处理, 2013, 29(9): 1206-1211.

WANG Wenjie, LI Xiaoping. The closed-form robust Chinese remainder theorem and its application in frequency estimation with undersampling [J]. Journal of Signal Processing, 2013, 29(9): 1206-1211.

[14]WANG Zengkun, YANG Zhibo, WU Shuming, et al. An improved multiple signal classification for nonuniform sampling in blade tip timing [J]. IEEE Transactions on Instrumentation and Measurement, 2020, 69(10): 7941-7952.

[16]李致铭, 兰哲冲, 金楷越, 等. 寄生电容自适应抑制的飞法级电容传感器读出电路 [J]. 西安交通大学学报, 2021, 55(5): 154-161.

LI Zhiming, LAN Zhechong, JIN Kaiyue, et al. A readout circuit for femtofarad-level capacitive sensors with parasitic capacitance suppression [J]. Journal of Xi’an Jiaotong University, 2021, 55(5): 154-161.

[17]JAMIA N, FRISWELL M I, EL-BORGI S, et al. Modelling and experimental validation of active and passive eddy current sensors for blade tip timing [J]. Sensors and Actuators: A Physical, 2019, 285: 98-110.

[18]ZHANG Jilong, DUAN Fajie, NIU Guangyue, et al. A blade tip timing method based on a microwave sensor [J]. Sensors, 2017, 17(5): 1097.

[19]宋昱, 孙文赟, 陈昌盛. 对数变换主成分分析的图像识别 [J]. 西安交通大学学报, 2021, 55(1): 33-42.

SONG Yu, SUN Wenyun, CHEN Changsheng. Logarithm transformation based principal component analysis for image recognition [J]. Journal of Xi’an Jiaotong University, 2021, 55(1): 33-42.

[20]WANG Zengkun, YANG Zhibo, WU Shuming, et al. An OPR-free blade tip timing method for rotating blade condition monitoring [J]. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 1-11.