一种有效的元认知线索：变化的时间规律性

容翠亮 冼美君 邢 强

（1 广州大学心理系，广州 510006；2 广东行政职业学院（广东青年职业学院），广州 510800）

1 引言

人们在生活中常常会根据某些线索做出判断和决策，元认知判断也不例外。 元认知判断（metacognitive judgments） 是指个体对当前认知活动及其未来表现进行评估和预测（Jackson et al.，2012）。 自信判断（confidence judgment）是其中的一种元认知判断，它指的是对当前项目记忆的确定程度进行判断（Nelson ＆ Narens，1994； Koriat，2007）。 元认知判断会受到多种线索的影响，而流畅性是其中一种重要的线索（Alter ＆ Oppenheimer，2009）。 以往大多研究都把流畅性定义为速度和准确性，即个体对刺激的反应越快，反应时间越短，元认知判断就越准 确 （Hertzog，Dunlosky，Robinson，＆ Kidder，2003； Thompson et al.，2013）。 尽管这是定义流畅性的一种常用方法，但是Stevenson 和Carlson（2018）提出这种以速度来定义流畅性程度的方法并不适合来定义个体在多步骤、 熟练的任务 （multistep，skilled tasks）中的流畅性。 例如，尽可能快地演奏钢琴和流畅地演奏钢琴是不同的，并不是越快就越准确。 他们认为在多步骤、熟练的任务中，应当将平稳（smoothness）而不是速度作为一种流畅性线索。 因此，他们将流畅性定义为时间规律性（temporal regularity），将时间规律性操作为一个星号开始呈现到下一个星号开始呈现的时间间隔（SOA），并采用数数范式（数星号）探究时间规律能否作为元认知线索。结果发现，从无规律性到规律性的转换导致个体在一致的时间规律条件下有更高的自信判断，验证了一致的时间规律性可作为一种元认知线索（Stevenson ＆ Carlson，2018）。

Stevenson 和Carlson（2018）的研究关注了一致的时间规律和无时间规律，结果发现时间规律性可以作为一个很重要的元认知线索。然而，时间规律性不仅包括一致的时间规律性，还有变化的时间规律性，包括递增变化的时间规律性、递减变化的时间规律性。 这种变化的时间规律性能否作为一种元认知线索，进而影响元认知判断？若变化的时间规律性可以作为元认知线索，那么与一致的时间规律性相比，它的元认知线索有效性是否更高？ 这是本研究将考察的问题。

时间规律性允许人们预测之后信息的时间轨迹，从而促进认知加工过程。 Schwartze，Rothermich，Schmidt－Kassow 和Kotz （2011）研究发现时间规律性影响注意加工过程，增强注意加工相关的认知机制。 Selchenkova，Jones 和Tillmann （2014）发现，相比无规律的时间期待，规律的时间期待可以提高其行为成绩。在变化时间的条件下，变化的时间规律允许人们预测和期待接下来要出现的信息，从而促进对任务的加工过程，这可能导致变化的时间规律比变化的无时间规律有着更高的成绩。 所以当个体对当前任务进行监控时就会利用这种变化的时间规律性作为线索，在变化的时间规律条件下可能出现更高的自信判断。 而且Stevenson 和Carlson（2018）的研究表明一致时间规律性能够作为促进认知加工的一种线索，并且变化的时间也存在时间规律。那么，在多步骤熟练的任务下，相比无时间规律，人们在元认知监控的过程中可能也会利用这种时间规律。 所以本研究操控变化的时间规律性考察变化的时间规律性能否作为元认知的一种线索。

根据动态注意理论（dynamic attending theory，DAT），外部规律可以激发内部振荡器，引导注意随时间的变化，帮助人们形成影响对未来事件感知的时间期待（Jones，1976）。Large 和Jones （1999）认为注意能量是一个动态变化的过程，而不是固定不变的，当外界出现有规律的时间节奏时，注意能量会以动态震荡的形式进行。 虽然注意资源的分配自发地遵循着一个内在的节奏，但这些节奏可以与一个外在规律的节奏产生同步，从而能够促进其加工。在熟练多步骤的数数任务中，相比一致的时间规律，递增变化的时间规律可能更容易与内在注意震荡产生同步，从而更能影响元认知判断。 然而，知觉时间压力也是影响认知加工过程的一个重要因素，有研究发现，相较于无时间压力，元认知判断在时间压力下的判断值更低（Benjamin，2005）。 人们在知觉到时间压力的情况下，会被认为认知资源减少。递增变化的时间规律和递减变化的时间规律可能在知觉时间压力上存在差异。相比递增的时间规律，递减变化的时间规律随着时间逐渐减少，可能需要更多的认知资源，任务成绩就会更低。 前人研究发现，流畅性程度主要取决于相对流畅性水平，而非绝对流畅性水平。相对流畅性是指当个体同时经历到两种或两种以上的知觉体验时，流畅性才能产生效应；绝对流畅性是指个体分别经历两种或两种以上的知觉体验而产生的 流 畅 性 体 验 （Westerman，2008 ； Wanke ＆Hansen，2015）。 和其他类型的流畅性一样，元认知判断依赖于时间流畅性的程度。因此，通过比较变化的时间规律性和一致的时间规律性产生的时间流畅性差异，本研究进一步探究这两者作为元认知线索的有效性程度。

综上所述，本研究使用数数范式考察变化的时间规律性能否作为一种元认知线索，以及比较变化的时间规律性和一致的时间规律性作为元认知线索的有效性。研究推测，当在递增或递减变化的时间规律性条件下，被试报告的正确率和自信判断显著高于无时间规律变化条件； 递增变化的时间规律性各项成绩最好，其次是一致的时间规律性，最后是递减的时间规律性。

2 实验1

2.1 实验目的

实验旨在考察变化的时间规律性是否可以作为一种元认知线索，假设变化的时间规律性在自信判断和正确率上显著高于无时间规律性。

2.2 方法

2.2.1 被试

选取72 名（36 女生） 大学生为被试，年龄为17～25 岁（M＝19.66，SD＝1.75），随机分配到三种不同的实验条件，每种条件24 人。 所有被试视力或矫正视力正常，之前均没有参加过类似的实验。 使用Gpower3.1 软件对统计检验功效进行计算，误差概率设为0.05，效应量设为0.3，结果显示本实验的检验功效Power（1－β）＝0.89，满足统计学要求。

2.2.2 实验材料

实验材料参照Stevenson 和Carlson（2018）的研究，材料为36 号Courier New bold 字体的星号，星号数量为20～40 个，具体如图1。

图1 实验材料示例

2.2.3 实验设计

单因素被试间设计，自变量为变化的时间规律性（递增变化的时间规律性、 递减变化的时间规律性、无时间规律性），因变量为任务正确率和自信判断值。

2.2.4 实验程序

首先呈现一个800ms 的红色注视点，然后呈现一系列星号，每个星号呈现200ms，把规律性时间间隔操作为一个星号呈现开始到下一个星号呈现开始的时间。 递增变化的时间规律性时间间隔为250～1030 ms 递增，递增间距为20ms；递减的时间规律性时间间隔为1030～250ms 递减，递减间距为20ms；无时间规律性的时间间隔在250～1030ms 间随机呈现。 星号数目为20 至40 任意数目，总共为3 个block，每个block 有16 个试次。 一系列星号呈现之后要求被试回答星号总数，输入答案之后立即对答案进行自信心判断 （0 至100，0 表示完全不确定，100 表示完全确定），实验具体流程详见图2。

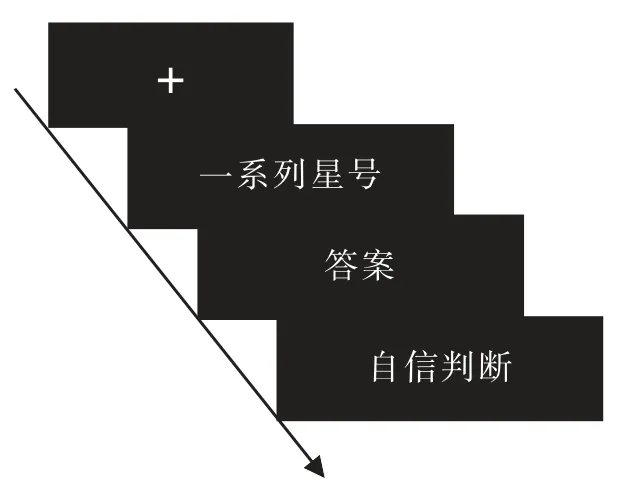
图2 实验1 流程图

2.3 结果与分析

数据分析参照Stevenson 和Carlson（2018）的研究，将自信判断评分和正确率作为一个因素进行统计分析来预测被试的自信情况。

使用SPSS20.0 程序进行3（block：1，2，3）×2（测量：自信判断值、正确率）×3（组别：递增变化的时间规律组、递减变化的时间规律组、无时间规律组）的重复测量方差分析，结果显示：测量的主效应显著F（1，69）＝2747.791，p＜0.001，η2p＝0.976；自信判断均值（M＝81.054%，SD＝1.546）高于正确率（M＝46.70%，SD＝2.3），如图3 所示。 Block 的主效应不显著，F（2，138）＝1.903，p＝0.153，η2p＝0.027；测量和block 的交 互 作 用 不 显 著，F （2，138）＝1.774，p＝0.174，η2p＝0.025。组别的主效应显著，F（1，69）＝5.259，p＝0.007，η2p＝0.132；测量和组别的交互作用显著，F（2，138）＝5.013，p＝0.009，η2p＝0.127；在自信判断值上，递增变化的时间规律组（M＝85.742%，SD＝2.677）和递减变化的时间规律组（M＝83.217%，SD＝2.677）无显著差异（p＝0.507），而递增变化的时间规律组显著高于无时间规律组 （M＝74.202%，SD＝2.677）（p＝0.003），递减变化的时间规律组显著高于无时间规律组 （p＝0.02）。 在正确率上，递增变化的时间规律组 （M＝62.902%，SD＝0.04） 显著高于递减变化的时间规律组（M＝40%，SD＝0.04）和无时间规律组（M＝37%，SD＝0.04）（p＜0.001），递减变化的时间规律组和无时间规律组无显著差异（p＝0.594）。 block 与组别的交互作 用 差 异 不 显 著，F （4，138）＝2.201，p＝0.072，η2p＝0.061； 测量、block 与组别三者交互作用不显著，F（4，138）＝2.251，p＝0.067，η2p＝0.061。

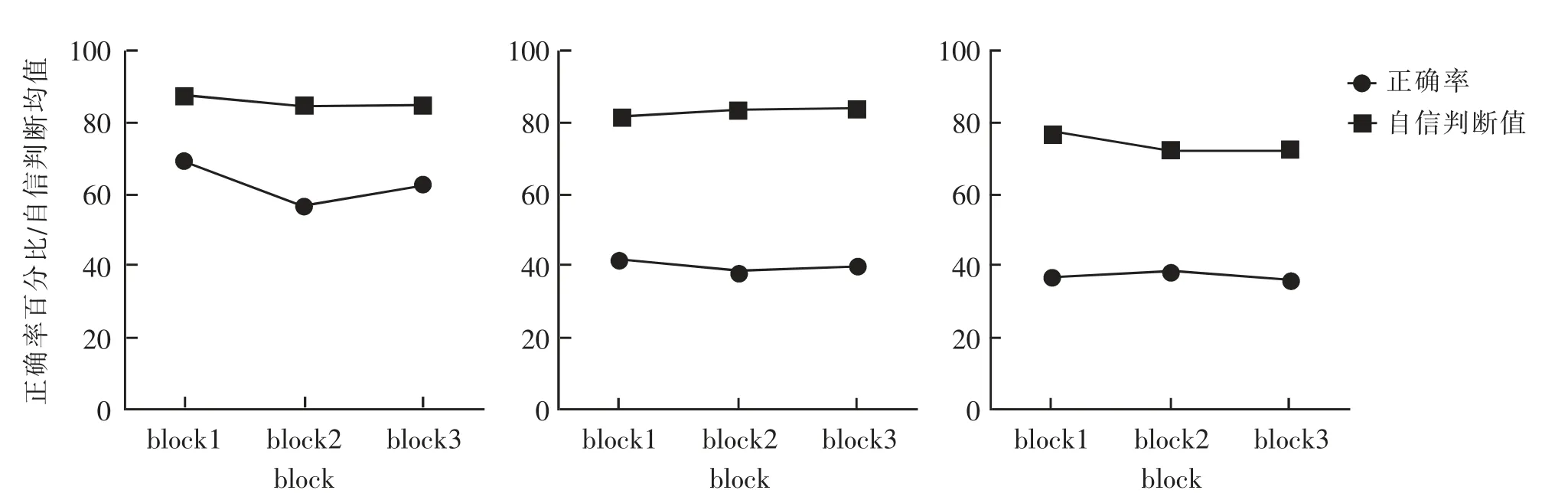
图3 不同组被试的自信情况

实验1 操控了变化的时间规律，包括递增变化的时间规律、递减变化的时间规律和无时间规律。在统计结果上，自信判断值都高于正确率，表明被试出现过度自信现象。 递增变化的时间规律组和递减变化的时间规律组在自信判断值上都显著高于无时间规律组，然而递增变化的时间规律组在正确率上显著高于递减变化的时间规律组和无时间规律组，递减变化的时间规律组的正确率高于无时间规律组，但是无显著差异。 这些结果表明变化的时间规律性可以作为正确率的有效线索，元认知判断可以依赖于变化的时间规律性。

3 实验2

3.1 实验目的

实验1 考察了变化的时间规律能否作为一种元认知线索，结果表明变化的时间规律影响自信判断。但是从实验1 结果看，被试报告相对高的自信判断有相对高的正确率，虽然递减变化的时间规律组和无时间规律组的正确率无显著差异，但是存在变化的 趋 势。 Undorf，Anke Söllner 和Arndt Bröder（2018）研究发现人们做元认知判断时会整合多个线索，可能是任务相关线索，也可能是任务无关线索。因此，实验1 不能确定被试做元认知判断过程是依赖于由时间操控所激发的流畅性体验，还是依赖于对实际错误的更直接的认识。基于此，有必要排除依赖于对实际错误认识的因素，减少递增变化的时间规律的平均时间，进一步探究变化的时间规律性是否可以作为元认知线索。 实验假设递增变化的时间规律将继续保持相对高的自信判断，但正确率较低。

3.2 方法

3.2.1 被试

选取大学生49 人（33 个女生）为被试，年龄为17～26（M＝19.53，SD＝1.64）岁。 递增变化的时间规律组为24 人，更快的递增变化的时间规律组为25 人，所有被试视力或矫正视力正常，所有被试均没有参加过类似的实验。 使用Gpower3.1 软件对统计检验功效进行计算，误差概率设为0.05，效应量设为0.3，结果显示本实验的检验功效Power （1－β）＝0.83，满足统计学要求。

3.2.2 实验材料

实验材料同实验1。

3.2.3 实验设计

单因素被试间设计，自变量为递增时间规律（递增变化的时间规律性，更快的递增变化的时间规律性），因变量为任务正确率和自信判断值。

3.2.4 程序

程序同实验1，除了星号与星号呈现的时间间隔不同。 更快的递增变化规律组被操作为第一个星号呈现和下一个星号呈现之间的时间间隔为250ms 递增。

3.3 结果与分析

数据分析方法同研究1，对3（block：1，2，3）×2（测量：自信评分、正确率）×2（组别：递增变化的时间规律组、更快的递增变化的时间规律组）进行重复测量方差分析，结果显示： 测量的主效应显著，F（1，47）＝3566.801，p＜0.001，η2p＝0.987；自信判断均值（M＝87.168%，SD＝1.459） 高于正确率 （M＝52.90%，SD＝3.6），如图4 所示。block 的主效应不显著，F（2，94）＝2.534，p＝0.085，η2p＝0.051； 测量和block 的交互作用不显著，F（2，94）＝2.245，p＝0.112，η2p＝0.046。 组别的主效应不显著，F（1，47）＝0.827，p＝0.368，η2p＝0.017；测量和组别的交互作用不显著，F （2，94）＝1.093，p＝0.301，η2p＝0.023；在自信判断上，递增变化的时间规律组（M＝85.742%，SD＝2.084）和更快的递增变化的时间规律组（M＝88.593%，SD＝2.042）无显著差异（p＝0.33）。 在正确率上，递增变化的时间规律组 （M＝62.90%，SD＝0.052）显著高于更快的递增变化的时间规律组（M＝44.80%，SD＝0.051）（p＝0.016）。 block 与组别的交互作用不显著，F （2，94）＝0.092，p＝0.913，η2p＝0.002；测量、block 与组别三者交互作用不显著，F （4，94）＝0.064，p＝0.938，η2p＝0.001。

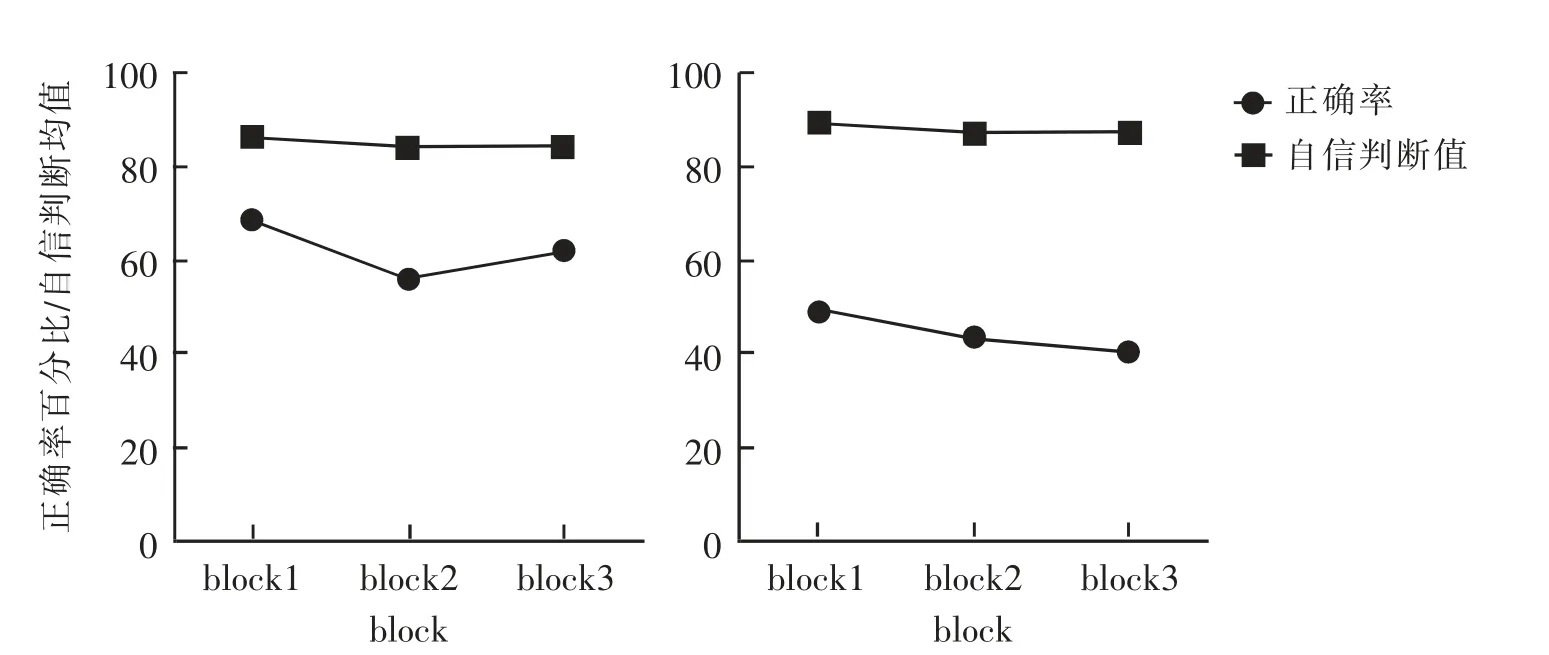
图4 不同递增时间规律被试的自信情况

实验2 增加一组平均SOA 更快的递增变化的时间规律组，考察变化的时间规律性能够作为元认知线索并不是因为对实际错误的直接认识。 结果发现，更快的递增变化时间规律组在自信判断上与递增变化的时间规律组无显著差异，而更快的递增变化的时间规律组在正确率上显著低于递增变化的时间规律组，出现了自信判断和正确率的分离现象，表明变化的时间规律与自信判断增高有关，变化的时间规律性可以作为一种元认知线索。

4 实验3

4.1 实验目的

实验1 和实验2 考察了变化的时间规律性可以作为一种元认知线索，结合Stevenson 和Carlson（2018）研究，一致的时间规律性也可作为一种元认知线索。那么，变化的时间规律性和一致的时间规律性哪个的元认知线索有效性更高？为此，实验3 考察变化的时间规律性和一致的时间规律性作为元认知线索的有效性差异。 研究假设递增变化的时间规律性各项成绩最好，其次是一致的时间规律性，最后是递减变化的时间规律性。

4.2 方法

4.2.1 被试

选取78 人（61 个女生，平均年龄为18.79 岁）大学生为被试，所有被试视力或矫正视力正常，所有被试均没有参加过类似的实验。 使用Gpower3.1 软件对统计检验功效进行计算，误差概率设为0.05，效应量设为0.3，结果显示本实验的检验功效Power（1－β）＝0.95，满足统计学要求。

4.2.2 材料

实验材料同实验1。

4.2.3 实验设计

单因素被试内设计，自变量为时间规律性（递增变化的时间规律性、递减变化的时间规律性、一致的时间规律性），因变量为任务正确率和自信判断评分。

4.2.4 程序

实验共分为3 个block，递增变化的时间规律组为1 个block，递减变化的时间规律组为1 个block，一致的时间规律组为1 个block。 每个block 有16 个试次。三组的平均时间相同，时间为340ms。3 个block顺序通过被试平衡。 实验具体程序同实验1。

4.3 结果与分析

数据分析方法同研究1，对3（时间规律性：递增变化的时间规律性、递减变化的时间规律性、一致的时间规律性）× 2（测量：自信评分、正确率）进行重复测量方差分析，结果显示：测量的主效应显著，F（1，77）＝219.759，p＜0.001，η2p＝0.741； 自信判断均值（M＝85.938%，SD＝1.108）高于正确率（M＝52.466%，SD＝1.971），如图5 所示。时间规律性的主效应显著，F（2，154）＝65.683，p＜0.001，η2p＝0.460；测量和时间规律 性 的 交 互 作 用 显 著，F （2，154）＝3752.234，p ＜0.001，η2p＝0.195，递增变化的时间规律性在自信判断和正确率上均显著大于递减变化的时间规律性（p＜0.001）；递减变化的时间规律性在自信判断和正确率上均显著小于一致时间规律性（p＜0.001）；递增变化的时间规律性在自信判断和正确率上均显著大于一致的时间规律性（p＝0.027；p＝0.016）。

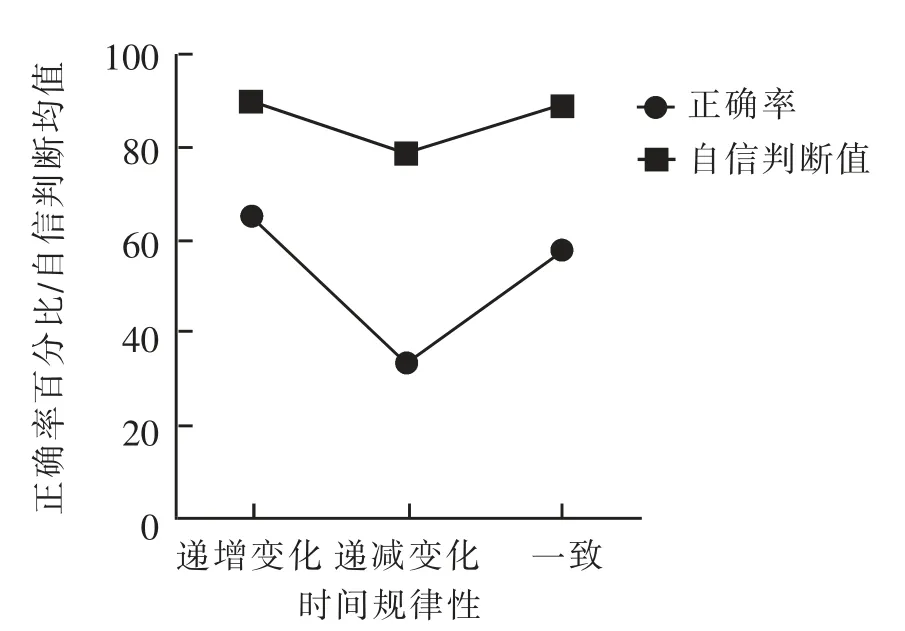
图5 三种时间规律性的自信判断值和正确率结果

实验3 考察了变化的时间规律性和一致的时间规律性之间的关系，变化的时间规律性能否作为元认知线索。 结果发现，三组都表现了过度自信的现象，递增变化的时间规律性无论在自信判断还是在正确率上都显著高于一致的时间规律性和递减变化的时间规律性，递减的时间规律性最差。实验结果符合预期假设，表明递增变化的时间规律性作为元认知线索的有效性程度更高。

5 总讨论

数数任务是典型的熟练的多步骤任务，本研究采用数数任务探究变化的时间规律性能否作为元认知线索，并考察变化的时间规律性和一致的时间规律性到底哪个更能作为元认知线索。 实验1 和实验2 探究变化的时间规律性是否能够作为元认知线索。 实验1 结果发现，相比无时间规律变化，变化的时间规律性有更高的自信判断，而递增变化的时间规律性的正确率比递减的时间规律性和无规律性更高。实验2 结果发现，递增变化的时间规律性和更快递增变化的时间规律性在自信判断上无差异，但在正确率上差异显著，出现了自信判断和正确率的分离。 两个实验结果表明变化的时间规律性可作为一种元认知线索。 实验3 通过比较变化的时间规律性和一致的时间规律性，考察哪种时间规律性的元认知线索有效性更高。 结果发现递增变化的时间规律性在转换条件下有更高的元认知线索有效性，其次是一致的时间规律性，最后是递减变化的时间规律性。三个实验都表现出被试过度自信现象，无论在规律的时间条件还是无规律条件下，自信判断都显著高于正确率。

变化的时间规律性组比无时间规律性组的自信判断更高，且在实验2 中出现自信判断和正确率的分离是由于被试流畅和不流畅体验驱使的。然而，研究者发现人们先前存在的信念在元认知判断中扮演着 重 要 的 作 用 （Kornell，Rhodes，Castel，＆Tauber，2011； Mueller，Dunlosky，Tauber，＆Rhodes，2014； Witherby，＆ Tauber，2016）。 因而，被试可能拥有关于变化的时间规律性相对任务难度的先前信念，从而影响自信判断结果，所以有必要评估个体关于变化的时间规律性相对任务难度的先前信念。对此，本研究另外招募了73 个被试（男生14 名），平均为19～27 岁（M＝20.54，SD＝1.75），对实验任务进行描述，要求被试发挥想象力。被试的任务如下：想象一下，在电脑屏幕呈现一个符号，接着再呈现一个符号，要求一个一个地数它们，在下列哪种条件下，自己能够准确地计算。 条件1：符号呈现越来越慢，第一符号呈现之后，接下来每个符号呈现的时候都在前一个符号呈现时间的基础上增加20ms，如250ms，270ms，290ms……递增呈现。条件2：符号呈现越来越快，第一个项目呈现之后，接下来每个符号呈现的时间在前一个符号呈现时间的基础上减少20ms，如1030ms，1010ms，990ms……递减呈现。 但呈现的平均时间和条件1 一样。 条件3：符号呈现的时间随机，如270ms，610ms，870ms……随机呈现，呈现的平均时间同条件1。 条件4：我想在三种情况下，都能同样准确地计算。 结果发现，四个答案存在显著差异。 递增变化的时间规律性占54.79%，递减变化的时间规律性占26.03%，无时间规律占10.96%，三种条件下都能准确计算的占8.22%。在评估信念结果上发现相似的结果，人们更多地认为变化的时间规律性条件下更能准确地计算，结果表明被试存在关于时间规律性影响准确率的先前信念。根据线索利用模型（Koriat，1997），人们在进行元认知判断时依赖于多种类型线索。 很多研究发现流畅性和信念在元认知判断中起到非常重要的作用，可能共同影响元认知判断 （Yan，Bjork，＆ Bjork，2016； Frank ＆ Kuhlmann，2017； Blake ＆ Castel，2018）。然而，Stevenson 和Carlson（2018）的研究发现自信判断依赖于流畅性体验，而不依赖个体先前存在的信念。 结果的差异可能是被试在评估信念时操作的平均间隔时间相同导致的，而在Stevenson和Carlson（2018）的研究中，时间规律性条件的间隔200ms，而无时间规律的间隔是在200ms，400ms 或500ms 中随机呈现，被试可能存在时间越长计算越准确的信念。

变化的时间规律性如何作为一种元认知线索影响元认知监控，并且递增变化的时间规律性比一致的时间规律性作为元认知线索的有效性程度更高呢？ 对其主要解释有以下几点：第一，变化的时间规律性作为元认知线索，一方面可能是被试主观体验之间的差异，相比变化的规律时间，在无时间规律性条件下的被试体验更不流畅，认为自己更可能出现错误； 另一方面可能是被试在这个实验过程中意识到时间规律性对其自信判断的影响，认为无时间规律性更难。 Snyder 和Logan（2013）研究发现在熟练的打印任务中外显的监控会干扰任务成绩，因而在无时间规律条件下准确率更低。第二，变化的时间规律性有更高的自信判断，但是在正确率上却出现差异。 一方面，这可能是知觉时间压力差异所导致的。前人研究发现，在时间压力条件下，认知资源会减少（Benjamin，2005； Karlos，Albuquerque，＆Martín－Luengo Beatriz，2018）。 虽然平均间隔时间相同，但是随着数量的增加，相比其他条件，递增变化的时间规律性有更多时间进行认知加工。 另一方面，这也可能是注意刷新时间上的差异导致的，注意刷新是指对不呈现的信息做一个简单的思考。 研究发现时间规律性可以提高注意刷新能力（Johnson ＆Marcia，1992）。 在递增变化的时间条件下，随着时间的增多，被试有更多的时间来进行注意刷新，从而提高任务成绩。 相反，递减变化的时间条件下，随着时间的减少，数数任务的增加，个体来不及刷新和维持，因而减少了任务成绩的准确性。 第三，Large 和Jones （1999）认为当外界出现具有规律时间结构的刺激时，注意能量会以动态振荡的形式展开。注意振荡能够与外界呈现刺激的规律产生同步，如果下个刺激出现的时间与注意振荡的波峰相位重合，能够促进它的加工（邱俊杰，黄希庭，于晓琳，2017）。被试在递增变化的时间规律性情况下更易与注意振荡产生同步，而一致的时间规律性和递减的时间规律性没有那么容易与内部规律形成同步，因而递增变化的时间规律性更能作为元认知线索。

本研究发现所有条件下被试的自信判断显著高于正确率，说明被试出现过度自信的现象。 Logan 和Crump（2010）提出层次反馈循环（hierarchical feedback loops），内部循环和外部循环使用不同的机制来识别错误的存在，而人们可能没有明确察觉到内部循环的错误。在熟练的多步骤的数数任务中，被试可能没有意识到错误的发生，因而在判断当前任务时，更多地利用时间规律性为线索，所以普遍高估自己的判断，从而导致过度自信的现象。

本研究进一步拓展了Stevenson 和Carlson（2018）的研究，发现变化的时间规律性可以作为元认知线索，且相比于一致的时间规律性更能作为元认知线索。当然，本研究也存在以下两点局限：第一，对变化的时间规律性的探究是在没有转化的条件下进行的，被试没有同时体验到各变化时间规律性和无规律性之间的不同； 第二，Stevenson 和Carlson（2018）发现一致的时间规律性影响自信判断是基于流畅性，而本研究发现变化的时间规律性也受到先前信念的影响，关于其影响机制及两种机制间的差异需要今后进一步探究。

6 结论

变化的时间规律性能够作为元认知线索，且递增变化的时间规律性相比于一致的时间规律性和递减变化的时间规律性作为元认知线索的有效性更高。